沪教版(五四学制)九年级数学上册教案:24.1放缩与相似形
文档属性
| 名称 | 沪教版(五四学制)九年级数学上册教案:24.1放缩与相似形 |
|
|
| 格式 | zip | ||
| 文件大小 | 64.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-25 10:23:33 | ||
图片预览


文档简介
课题:放缩与相似形
教学内容:
一、相似形
1、图形的放缩运动:图形的放大或缩小,称为图形的放缩运动。
2、相似形:我们把形状相同的两个图形称为相似的图形,简称相似形。
3、相似形的特点:大小不一定相等,形状相同。
4、多边形相似的特点:同为边形,并且形状相同,对边角相等,对应边成比例。
二、多边形相似的含义
如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边成比例。
当两个相似的多边形是全等形时,它们的对应边的长度比值都是1。
精解名题:
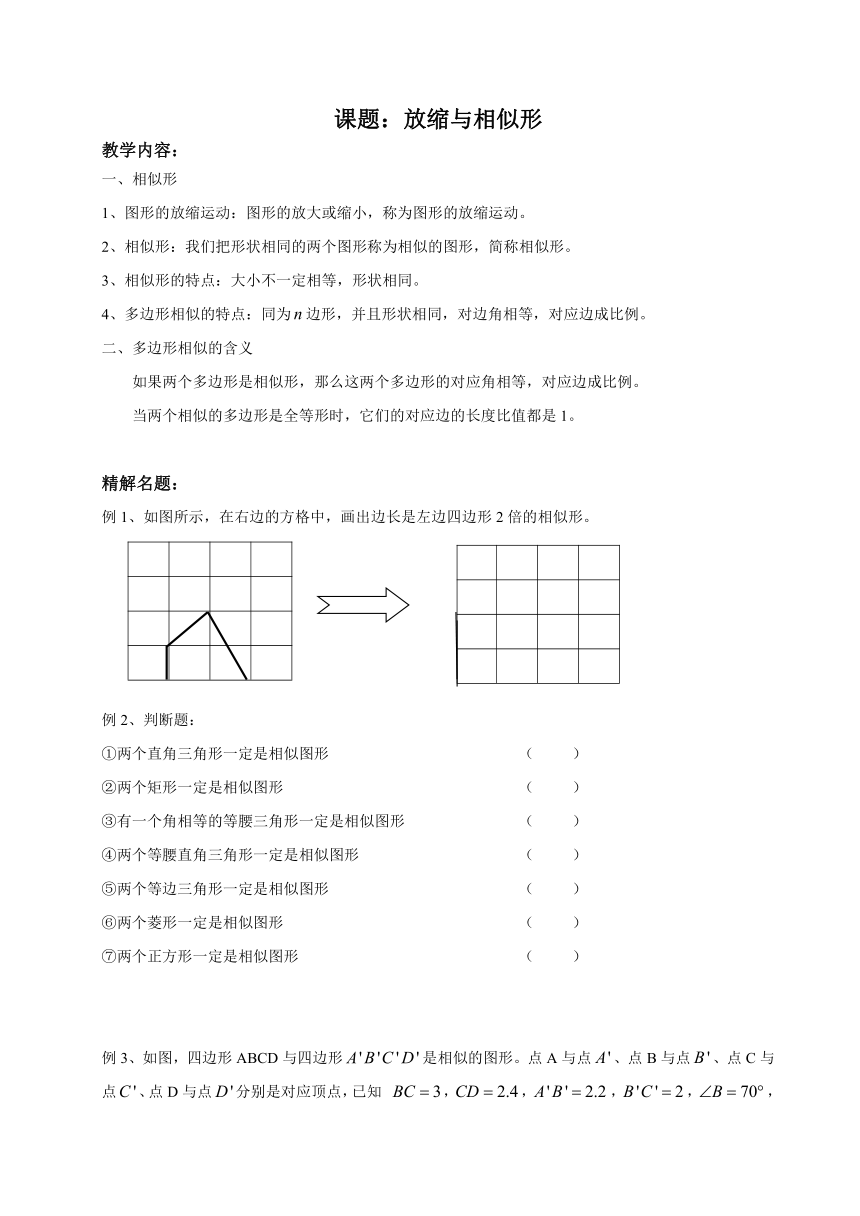
例1、如图所示,在右边的方格中,画出边长是左边四边形2倍的相似形。
例2、判断题:
①两个直角三角形一定是相似图形 ( )
②两个矩形一定是相似图形 ( )
③有一个角相等的等腰三角形一定是相似图形 ( )
④两个等腰直角三角形一定是相似图形 ( )
⑤两个等边三角形一定是相似图形 ( )
⑥两个菱形一定是相似图形 ( )
⑦两个正方形一定是相似图形 ( )
例3、如图,四边形ABCD与四边形是相似的图形。点A与点、点B与点、点C与点、点D与点分别是对应顶点,已知 ,,,,,,,求边AB、的长和的度数。
( http: / / www.21cnjy.com )
例4、如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 ; B.27cm2 ; C.21cm2 ; D.20cm2.
例5、已知:与中,,,,,。则与相似吗?为什么?
例6、一张长方形纸片对折后所得的长方形与原长方形是相似形,则原长方形的长与宽的比是多少?
巩固练习:
1、ΔABC与△DEF中,,,,,,,,,,,则△DEF 与△ABC_____
2、下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个; B.4个; C.5个; D.6个.
3、矩形ABCD中,,矩形EFGH中,,,这两个矩形_____
4、△ABC的三条边之比为,与其相似的另一个△最大边长为18cm,则另两边长的和为_______.
5、要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,则另外一个三角形的周长为
6、蛋糕店制作两种高度相同的圆柱形蛋糕, ( http: / / www.21cnjy.com )一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕能够2个人吃,半径是30cm的蛋糕能够 个人吃。
课堂小结:
1、相似图形的定义
2、判断相似图形
3、相似多边形的性质特征
自我测试:
1、下列说法正确的是( )
A.对应边都成比例的多边形相似; B.对应角都相等的多边形相似;
C.边数相同的正多边形相似; D.矩形都相似.
2、在相似三角形中,已知其中一个三角形三边的长是4、6、8,另一个三角形的一边长是2,则另一个三角形的周长是( )
A.4.5; B.6; C.9; D.以上答案都有可能.
3、如图,已知D、E分别在△ABC的AB、AC边上,△ABC与△ADE相似,则下列各式成立的是( )
A.; B.;
C.; D..
4、如果把三角形各顶点的纵、横坐标都乘以,得到△,则这两个三角形在坐标中的位置关系是( )
A.关于轴对称; B.关于轴对称; C.关于原点对称; D.无对称关系.
5、已知:如图,在△ABC中,D、E分别在AC、AB上,且△ABC与△ADE是相似形,其中点A、B、C的对应点分别是点A、D、E。,,,,求:DE、DC的长
6、在方格图中,画出和四边形ABCD相似的一个相似图形。
( http: / / www.21cnjy.com )
7、M在AB上,且,,。在AC上求作一点N,使△AMN与原三角形相似,并求AN的长。
8、如图,所示的两个矩形是否相似?并简单说明理由。
12
20
12
5
5
3
3
教学内容:
一、相似形
1、图形的放缩运动:图形的放大或缩小,称为图形的放缩运动。
2、相似形:我们把形状相同的两个图形称为相似的图形,简称相似形。
3、相似形的特点:大小不一定相等,形状相同。
4、多边形相似的特点:同为边形,并且形状相同,对边角相等,对应边成比例。
二、多边形相似的含义
如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边成比例。
当两个相似的多边形是全等形时,它们的对应边的长度比值都是1。
精解名题:
例1、如图所示,在右边的方格中,画出边长是左边四边形2倍的相似形。
例2、判断题:
①两个直角三角形一定是相似图形 ( )
②两个矩形一定是相似图形 ( )
③有一个角相等的等腰三角形一定是相似图形 ( )
④两个等腰直角三角形一定是相似图形 ( )
⑤两个等边三角形一定是相似图形 ( )
⑥两个菱形一定是相似图形 ( )
⑦两个正方形一定是相似图形 ( )
例3、如图,四边形ABCD与四边形是相似的图形。点A与点、点B与点、点C与点、点D与点分别是对应顶点,已知 ,,,,,,,求边AB、的长和的度数。
( http: / / www.21cnjy.com )
例4、如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 ; B.27cm2 ; C.21cm2 ; D.20cm2.
例5、已知:与中,,,,,。则与相似吗?为什么?
例6、一张长方形纸片对折后所得的长方形与原长方形是相似形,则原长方形的长与宽的比是多少?
巩固练习:
1、ΔABC与△DEF中,,,,,,,,,,,则△DEF 与△ABC_____
2、下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个; B.4个; C.5个; D.6个.
3、矩形ABCD中,,矩形EFGH中,,,这两个矩形_____
4、△ABC的三条边之比为,与其相似的另一个△最大边长为18cm,则另两边长的和为_______.
5、要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,则另外一个三角形的周长为
6、蛋糕店制作两种高度相同的圆柱形蛋糕, ( http: / / www.21cnjy.com )一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕能够2个人吃,半径是30cm的蛋糕能够 个人吃。
课堂小结:
1、相似图形的定义
2、判断相似图形
3、相似多边形的性质特征
自我测试:
1、下列说法正确的是( )
A.对应边都成比例的多边形相似; B.对应角都相等的多边形相似;
C.边数相同的正多边形相似; D.矩形都相似.
2、在相似三角形中,已知其中一个三角形三边的长是4、6、8,另一个三角形的一边长是2,则另一个三角形的周长是( )
A.4.5; B.6; C.9; D.以上答案都有可能.
3、如图,已知D、E分别在△ABC的AB、AC边上,△ABC与△ADE相似,则下列各式成立的是( )
A.; B.;
C.; D..
4、如果把三角形各顶点的纵、横坐标都乘以,得到△,则这两个三角形在坐标中的位置关系是( )
A.关于轴对称; B.关于轴对称; C.关于原点对称; D.无对称关系.
5、已知:如图,在△ABC中,D、E分别在AC、AB上,且△ABC与△ADE是相似形,其中点A、B、C的对应点分别是点A、D、E。,,,,求:DE、DC的长
6、在方格图中,画出和四边形ABCD相似的一个相似图形。
( http: / / www.21cnjy.com )
7、M在AB上,且,,。在AC上求作一点N,使△AMN与原三角形相似,并求AN的长。
8、如图,所示的两个矩形是否相似?并简单说明理由。
12
20
12
5
5
3
3
