4.4 平行线的判定(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 4.4 平行线的判定(第2课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 11:49:31 | ||
图片预览






文档简介
(共23张PPT)
4.4 平行线的判定
第2课时 平行线的判定方法 2,3
1.使学生掌握利用内错角、同旁内角判定两直线平行的判定方法.
2.能运用所学过的平行线的判定方法,进行简单的推理和计算.
3.经历观察、操作、想象、推测、交流等活动,体会利用操作、归纳等方法获得数学结论的过程,进一步发展空间想象、推理能力和有条理的表达能力.
4.使学生在参与探索、交流的数学活动中,进一步体验数学与实际生活的密切联系.
【教学重点】会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
【教学难点】会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
问题 前面我们学了平行线的哪些判定方法?
平行于同一条直线的两条直线平行.
同位角相等,两直线平行.
思考 还有其他判定两条直线平行的方法吗?
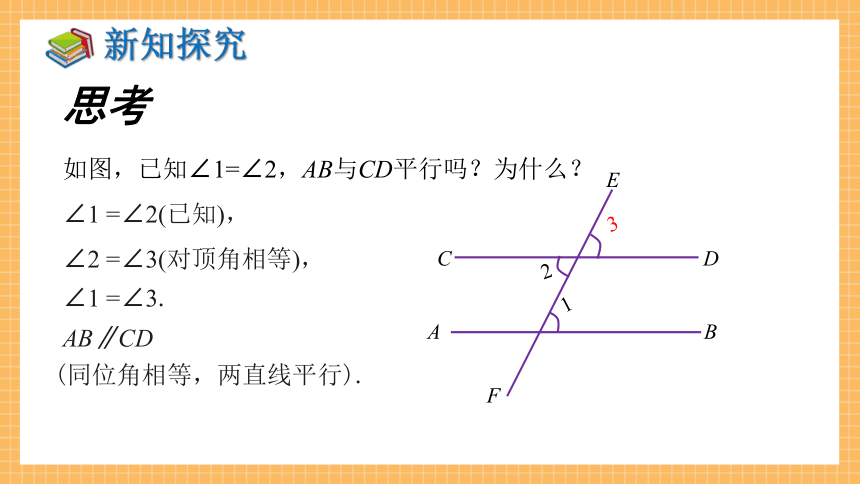
如图,已知∠1=∠2,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
3
∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
∠1 =∠3.
AB∥CD
(同位角相等,两直线平行).
思考
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
∠1=∠2,
AB∥CD.
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
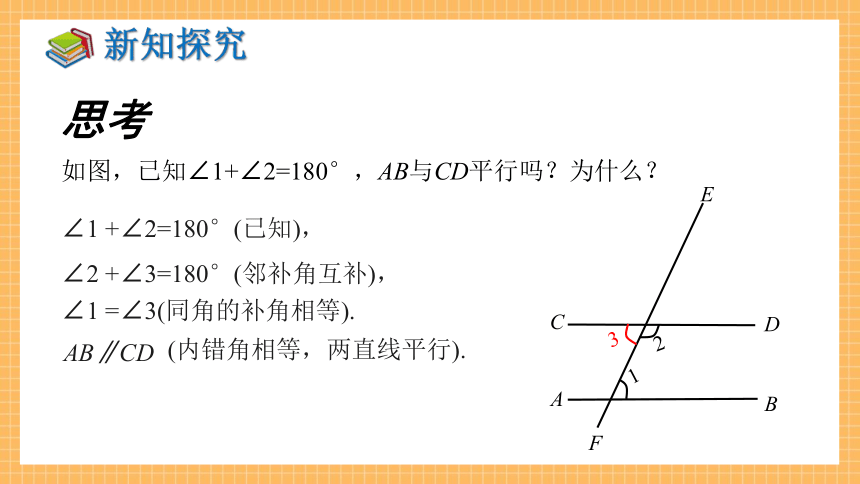
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
∠1 =∠3(同角的补角相等).
AB∥CD
(内错角相等,两直线平行).
3
思考
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
因为∠1 +∠2 = 180° (已知),
所以 a∥b (同旁内角互补,两直线平行).
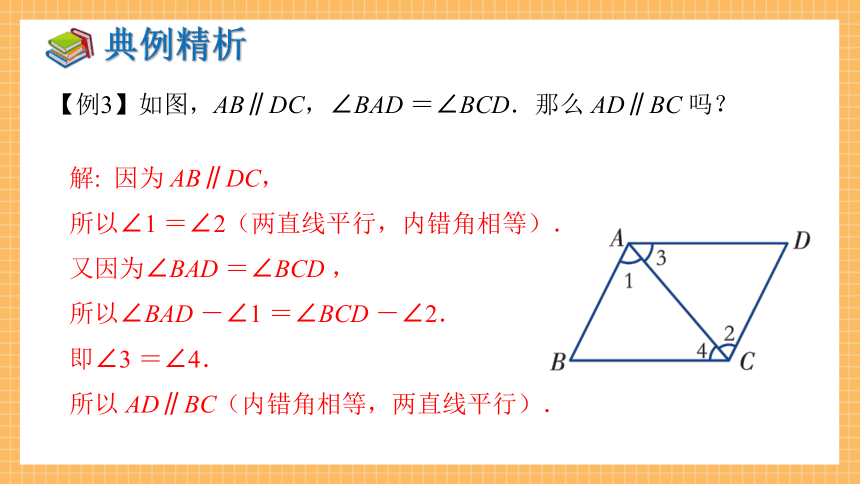
【例3】如图,AB∥DC,∠BAD =∠BCD.那么 AD∥BC 吗?
解: 因为 AB∥DC,
所以∠1 =∠2(两直线平行,内错角相等).
又因为∠BAD =∠BCD ,
所以∠BAD -∠1 =∠BCD -∠2.
即∠3 =∠4.
所以 AD∥BC(内错角相等,两直线平行).
① 因为 ∠2 =∠6(已知),
所以 ___∥___ ( ).
② 因为 ∠3 =∠5(已知),
所以 ___∥___ ( ).
③ 因为 ∠4 +___ =180°(已知),
所以 ___∥___ ( ).
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
F
E
1、根据条件完成填空:
① 因为 ∠1 =_____ (已知),
所以 AB∥CE ( ).
② 因为 ∠1 +_____= 180° (已知),
所以 CD∥BF ( ).
③ 因为 ∠1 +∠5 = 180° (已知),
所以 ____∥____ ( ).
AB
CE
∠2
④ 因为 ∠4 +_____= 180° (已知),
所以CE∥AB ( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
2、根据条件完成填空:
【例4】如图,∠1=∠2= 50o , AD∥BC, 那么 AB∥DC 吗?
解:因为AD∥BC,
所以∠1 + ∠3 = 180o
(两直线平行,同旁内角互补).
则∠3 = 180o -∠1
= 180o - 50o = 130o .
所以∠2 + ∠3 = 50o + 130o = 180o.
所以 AB∥DC(同旁内角互补,两直线平行).
1
2
3
A
C
D
B
所以 AB∥MN(内错角相等,两直线平行).
因为 ∠MCA =∠A(已知),
又因为∠DEC =∠B(已知),
所以 AB∥DE(同位角相等,两直线平行).
所以 DE∥MN(平行于同一条直线的两条直线平行).
3、如图,已知∠MCA =∠A,∠DEC =∠B,那么DE∥MN 吗?为什么?
A
E
B
C
D
N
M
解:DE∥MN. 理由如下:
4、如图,已知 ∠1 = 75°,∠2 = 105°,问:AB 与 CD 平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75°
105°
1. 如图,点 A 在直线 l 上,如果∠B = 75°,∠C = 43°,则
(1) 当∠1 =_____时, 直线 l ∥ BC;
(2) 当∠2 =_____时, 直线 l ∥ BC.
75°
43°
2. 如图,可以确定 AB∥CE 的条件是 ( )
A. ∠2 =∠B
B. ∠1 =∠A
C. ∠3 =∠B
D. ∠3 =∠A
C
1
2
3
A
E
B
C
D
3. 如图所示,下列条件中不能判定 DE∥BC 的是( )
A. ∠1 =∠C
B. ∠2 =∠3
C. ∠1 =∠2
D. ∠2 +∠4= 180°
C
4. 如图. (1) 从∠1 =∠4,可以推出 ∥ ,理由
是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
5、已知∠3 = 45°,∠1 与∠2 互余,试说明:AB//CD.
解:因为∠1 = ∠2 (对顶角相等),
∠1+∠2 = 90° (已知),
所以∠1 = ∠2 = 45°.
因为∠3 = 45° (已知),
所以∠ 2 =∠3.
所以 AB∥CD (内错角相等,两直线平行).
1
2
3
A
B
C
D
理由:
因为 AC 平分∠DAB (已知),
所以∠1 =∠2 (角平分线的定义).
又因为∠1 = ∠3 (已知),
所以∠2 =∠3 (等量代换).
所以 AB∥CD (内错角相等,两直线平行).
6. 如图,已知∠1 = ∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
7. 已知:如图,∠ABC = 90°,∠1+∠2=90°,∠2=∠3. BE∥DF 吗?为什么?
解 : BE∥DF.
理由:因为∠1+∠2=90°,∠2=∠3,
所以∠1+∠3=90°,
又因为∠ABC = 90°,
所以∠3+∠4=90°,
所以∠1=∠4,
所以BE∥DF (同位角相等,两直线平行).
1. 同位角相等,两直线平行.
2. 内错角相等,两直线平行.
3. 同旁内角互补,两直线平行.
4. 平行于同一条直线的两直线平行.
5. 平行线的定义.
判定两条直线是否平行的方法有:
1. 习题4.4中第5、7、8题.
2.完成同步练习册中本课时的练习.
4.4 平行线的判定
第2课时 平行线的判定方法 2,3
1.使学生掌握利用内错角、同旁内角判定两直线平行的判定方法.
2.能运用所学过的平行线的判定方法,进行简单的推理和计算.
3.经历观察、操作、想象、推测、交流等活动,体会利用操作、归纳等方法获得数学结论的过程,进一步发展空间想象、推理能力和有条理的表达能力.
4.使学生在参与探索、交流的数学活动中,进一步体验数学与实际生活的密切联系.
【教学重点】会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
【教学难点】会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
问题 前面我们学了平行线的哪些判定方法?
平行于同一条直线的两条直线平行.
同位角相等,两直线平行.
思考 还有其他判定两条直线平行的方法吗?
如图,已知∠1=∠2,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
3
∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
∠1 =∠3.
AB∥CD
(同位角相等,两直线平行).
思考
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
∠1=∠2,
AB∥CD.
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
∠1 =∠3(同角的补角相等).
AB∥CD
(内错角相等,两直线平行).
3
思考
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
因为∠1 +∠2 = 180° (已知),
所以 a∥b (同旁内角互补,两直线平行).
【例3】如图,AB∥DC,∠BAD =∠BCD.那么 AD∥BC 吗?
解: 因为 AB∥DC,
所以∠1 =∠2(两直线平行,内错角相等).
又因为∠BAD =∠BCD ,
所以∠BAD -∠1 =∠BCD -∠2.
即∠3 =∠4.
所以 AD∥BC(内错角相等,两直线平行).
① 因为 ∠2 =∠6(已知),
所以 ___∥___ ( ).
② 因为 ∠3 =∠5(已知),
所以 ___∥___ ( ).
③ 因为 ∠4 +___ =180°(已知),
所以 ___∥___ ( ).
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
F
E
1、根据条件完成填空:
① 因为 ∠1 =_____ (已知),
所以 AB∥CE ( ).
② 因为 ∠1 +_____= 180° (已知),
所以 CD∥BF ( ).
③ 因为 ∠1 +∠5 = 180° (已知),
所以 ____∥____ ( ).
AB
CE
∠2
④ 因为 ∠4 +_____= 180° (已知),
所以CE∥AB ( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
2、根据条件完成填空:
【例4】如图,∠1=∠2= 50o , AD∥BC, 那么 AB∥DC 吗?
解:因为AD∥BC,
所以∠1 + ∠3 = 180o
(两直线平行,同旁内角互补).
则∠3 = 180o -∠1
= 180o - 50o = 130o .
所以∠2 + ∠3 = 50o + 130o = 180o.
所以 AB∥DC(同旁内角互补,两直线平行).
1
2
3
A
C
D
B
所以 AB∥MN(内错角相等,两直线平行).
因为 ∠MCA =∠A(已知),
又因为∠DEC =∠B(已知),
所以 AB∥DE(同位角相等,两直线平行).
所以 DE∥MN(平行于同一条直线的两条直线平行).
3、如图,已知∠MCA =∠A,∠DEC =∠B,那么DE∥MN 吗?为什么?
A
E
B
C
D
N
M
解:DE∥MN. 理由如下:
4、如图,已知 ∠1 = 75°,∠2 = 105°,问:AB 与 CD 平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
75°
105°
1. 如图,点 A 在直线 l 上,如果∠B = 75°,∠C = 43°,则
(1) 当∠1 =_____时, 直线 l ∥ BC;
(2) 当∠2 =_____时, 直线 l ∥ BC.
75°
43°
2. 如图,可以确定 AB∥CE 的条件是 ( )
A. ∠2 =∠B
B. ∠1 =∠A
C. ∠3 =∠B
D. ∠3 =∠A
C
1
2
3
A
E
B
C
D
3. 如图所示,下列条件中不能判定 DE∥BC 的是( )
A. ∠1 =∠C
B. ∠2 =∠3
C. ∠1 =∠2
D. ∠2 +∠4= 180°
C
4. 如图. (1) 从∠1 =∠4,可以推出 ∥ ,理由
是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
5、已知∠3 = 45°,∠1 与∠2 互余,试说明:AB//CD.
解:因为∠1 = ∠2 (对顶角相等),
∠1+∠2 = 90° (已知),
所以∠1 = ∠2 = 45°.
因为∠3 = 45° (已知),
所以∠ 2 =∠3.
所以 AB∥CD (内错角相等,两直线平行).
1
2
3
A
B
C
D
理由:
因为 AC 平分∠DAB (已知),
所以∠1 =∠2 (角平分线的定义).
又因为∠1 = ∠3 (已知),
所以∠2 =∠3 (等量代换).
所以 AB∥CD (内错角相等,两直线平行).
6. 如图,已知∠1 = ∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
7. 已知:如图,∠ABC = 90°,∠1+∠2=90°,∠2=∠3. BE∥DF 吗?为什么?
解 : BE∥DF.
理由:因为∠1+∠2=90°,∠2=∠3,
所以∠1+∠3=90°,
又因为∠ABC = 90°,
所以∠3+∠4=90°,
所以∠1=∠4,
所以BE∥DF (同位角相等,两直线平行).
1. 同位角相等,两直线平行.
2. 内错角相等,两直线平行.
3. 同旁内角互补,两直线平行.
4. 平行于同一条直线的两直线平行.
5. 平行线的定义.
判定两条直线是否平行的方法有:
1. 习题4.4中第5、7、8题.
2.完成同步练习册中本课时的练习.
