2024年浙江省初中学业水平考试模拟演练数学试卷(含答案)
文档属性
| 名称 | 2024年浙江省初中学业水平考试模拟演练数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 00:00:00 | ||
图片预览



文档简介
浙江省2024年初中学业水平考试模拟演练
数学·试题卷
本试卷共6页,24小题,满分120分.考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考场号和座位号填写在答题卡上.用2B铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号.将条形码粘贴在答题卡“条形码粘贴处”.
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,只上交答题卡.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各式中,能用平方差公式分解因式的是
A.a2+4b2 B.﹣x2+16y2 C.﹣a2﹣4b2 D.a﹣4b2
2.下列计算正确的是
A. B.
C. D.
3.这段时间,一个叫“学习强国”的理论学习平台火了,截止4月2号,华为官方应用市场“学习强国APP”下载量已达88300000次,请将88300000用科学记数法表示为
A.0.883×106 B.8.83×107 C.8.83×108 D.88.3×109
4.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点.过点的直线l与⊙B相交于C、D两点,则弦长是整数值的条数有
A.2个 B.3个 C.4个 D.5个
5.满足下列条件的△ABC,不是直角三角形的是
A. B.
C. D.
6.小华的妈妈去年存了一个1年期存款,年利率为3.50%,今年到期后得到利息700元,小华的妈妈去年存款的本金为
A.1000元 B.2000元 C.10000元 D.20000元
7.现有一组统计数据:,,,,,,.对于不同的,下列统计量不会发生改变的是
A.众数、中位数 B.平均数、方差
C.平均数、中位数 D.众数、方差
8.把二次函数的图象作关于原点的对称变化,所得到的图象函数式为,若,则m最小值是
A.6 B.4 C.8 D.2
9.在数轴上,点A,B分别表示实数a,b,将点A向左平移1个单位长度得到点C,若点C,B关于原点O对称,则下列结论正确的是
A.a+b=1 B.a+b=﹣1 C.a﹣b=1 D.a﹣b=﹣1
10.如图,在△ABC中,,,,将△ABC绕点A顺时针旋转得到,当点落在边上时,连接,则线段的长为
A.3 B.1 C.2 D.
(第4题) (第10题)
二、填空题:本大题共6小题,每小题4分,共24分.
11.我们把分子是1的分数叫做分数单位,有些单位分数可以拆成两个不同的分数的差,如,请用观察到的规律解方程该方程的解是 ▲ .
12.现将一把直尺和的直角三角板按如图摆放,经测量得,则 ▲ .
13.若,则 ▲ .
14.在平面直角坐标系中,点,点P的“变换点”Q的坐标定义如下:当时,,当时,,线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 ▲ .
15.如图,在△ABC中,,点在边上,,将沿折叠,的对应边交于点,连接.若,则的长为▲.
(第12题) (第15题)
16.如图1,是一种锂电池自动液压搬运物体叉车,图2是叉车侧面近似示意图.车身为四边形ABCD,,BC⊥AB,底座AB上装着两个半径为30cm的轮胎切于水平地面,AB=169cm,BC=120cm.挡货架AE上有一固定点T与AD的中点N之间由液压伸缩杆TN连接.当TN⊥AD时,TN的延长线恰好经过B点,则AD的长度是 cm;一个长方体物体准备装卸时,AE绕点A左右旋转,托物体的货叉PQ⊥AE(PQ沿着AE可上下滑动),PQ=65cm,AE=AD.当AE旋转至AF时,PQ下降到P'Q'的位置,此时F,D,C三点共线,且FQ'=52cm,则点P'到地面的离是 ▲ cm.
(第16题)
三、解答题:本大题共8小题,其中17~19题各6分,20~21题各8分,22~23题各10分,24题12分,共66分.
17.(1)解方程组:;
(2)解不等式组.
18.(1)计算∶2sin245°-6sin 30°+3tan 45°+4cos 60°.
(2)小明在用公式法解方程x2-5x=2时出现了错误,解答过程如下∶
∵a=1,b=-5,c=2,(第一步)
∴b2-4ac=(-5)2-4×1×2=17,(第二步)
∴x,(第三步)
∴ x1,x2=.(第四步)
①小明的解答过程是从第 步开始出错的,其错误的原因是
②请你写出此题正确的解答过程.
19.已知平面上A(4,4),B(2,0),C(0,6)
(1)在下面的平面直角坐标系中找出A、B、C三点,绘制出△ABC.
(2)求出△ABC的面积.
(第19题)
20.《义务教育课程方案和课程标准(2022年版)》指出,劳动课成为中小学的一门独立课程.《大中小学劳动教育指导纲要(试行)》要求初中阶段劳动时长不少于3小时,某初级中学为了解本校学生每周劳动时长,组织数学兴趣小组按下列步骤开展统计活动.
确定调查对象:
从全校1500名学生中随机抽取部分学生,进行每周劳动时长调查.
收集整理数据:
按照标准,学生每周劳动时长分为A,B,C,D四个等级,数学兴趣小组随机抽取本校部分学生进行调查,绘制成下面不完整的统计图表.
分析数据,解答问题:
(1)本次调查中:1500名学生中每名学生每周的劳动时长是______(填“总体”或“个体”);统计表中的______,______.
(2)请估算该校学生中,每周劳动时长不符合要求的人数.
(3)为更好践行劳动教育要求,结合上述数据分析,请你提出一条合理化的建议.
21.根据以下素材,探索完成任务.
探究遮阳伞下的影子长度
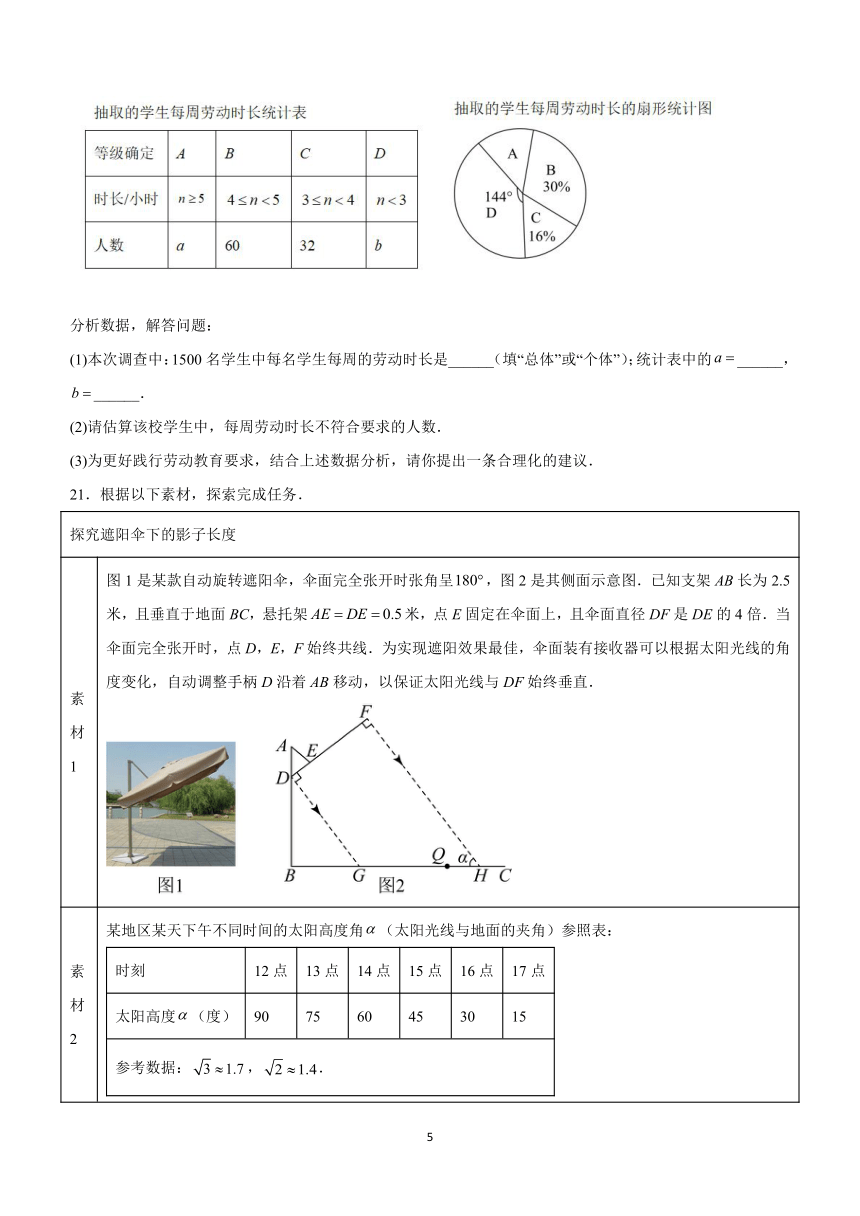
素材1 图1是某款自动旋转遮阳伞,伞面完全张开时张角呈,图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直.
素材2 某地区某天下午不同时间的太阳高度角(太阳光线与地面的夹角)参照表:时刻12点13点14点15点16点17点太阳高度(度)907560453015参考数据:,.
素材3 小明坐在露营椅上的高度(头顶到地面的距离)约为1米.如图2,小明坐的位置记为点Q.
问题解决
任务1 确定影子长度 某一时刻测得米,请求出此时影子的长度.
任务2 判断是否照射到 这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否会被太阳光照射到?
任务3 探究合理范围 小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算的取值范围.
22.如图,在平面直角坐标系中,线段AB的两个端点为A、B分别在y轴正半轴、x轴负半轴上,直线CD分别交x轴正半轴、y轴负半轴于点C、D,且AB∥CD.
(1)如图1,若点A(0,a)和点B(b,0)的坐标满足
ⅰ)直接写出a、b的值,a=_____,b=_____;
ⅱ)把线段AB平移,使B点的对应点E到x轴距离为1,A点的对应点F到y轴的距离为2,且EF与两坐标轴没有交点,则F点的坐标为_____;
(2)若G是CD延长线上一点DP平分∠ADG,BH平分∠ABO,BH的反向延长线交DP于P(如图2),求∠HPD的度数;
(3)若∠BAO=30°,点Q在x轴(不含点B、C)上运动,AM平分∠BAQ,QN平分∠AQC,(如图3)直接出∠BAM与∠NQC满足的数量关系.
(第22题)
23.已知抛物线与轴交于不同的两点
(1)求的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点,并求出点的坐标;
(3)当时,由(2)求出的点和点构成的的面积是否有最值?若有,求出该最值及相对应的值.
24.四边形是菱形,点O为对角线交点,边的垂直平分线交线段于点P(P不与O重合),连接,以点P为圆心,长为半径的圆交直线于点E,直线与直线交于点F,如图所示.
(1)当时,求证:直线与相切;
(2)当,时,求的度数;
(3)在菱形的边长与内角发生变化的过程中,若点C与E不重合,请探究与的数量关系.
浙江省2024年初中学业水平考试模拟演练
数学·参考答案
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B 2.B 3.B 4.B 5.A
6.D 7.A 8.D 9.A 10.C
二、填空题:本大题共6小题,每小题4分,共24分.
11. 12. 13.2
14. 15. 16. 130 77
三、解答题:本大题共8小题,其中17~19题各6分,20~21题各8分,22~23题各10分,24题12分,共66分.
17.(1)
①×2+②得,9x=9,即x=1,
把x=1代入②得:y=-1,
∴方程组的解是;
(2)
由①得,
由②得,
则不等式组的解集为.
18.解:(1)2sin245°-6sin 30°+3tan 45°+4cos 60°
=2×()2-6×+3×1+4×
=1-3+3+2
=3;
(2)①小明的解答过程是从第一步开始出错的,其错误的原因是原方程没有化成一般形式,
故答案为:一, 原方程没有化成一般形式;
②原方程变形为x -5x-2=0,
∴a=1,b=-5,c=-2,
∴b2-4ac=(-5)2-4×1×(-2)=33,
∴x,
∴x1,x2.
19.解:(1)如图△ABC即为所作:
(2):由勾股定理AB==2,
AC==2,
BC==2 ,
∵AB2+AC2=(2)2+(2)2=40,BC2=(2)2=40
∴AB2+AC2=BC2 ,
∴△ABC是直角三角形,
∴S△ABC=×2×2=10.
20.(1)解:1500名学生中每名学生每周的劳动时长是个体.
先计算D等级所占的百分比:
∴A等级所占的百分比是:
∴(人),(人).
故答案为:个体;28;80.
(2)(人),
答:估算该校学生中,每周劳动时长不符合要求的人数有600人;
(3)每周劳动时长不符合要求的占,说明学生平时劳动的时间非常少,建议学校加强劳动教育,多开展一些劳动课.
21.解:(1)如图1,过点E作于点I,过点G作于点J.
∵,,
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∵,四边形为矩形,
∴,,
∴,
∴,
在中,(米).
(2)方法1:
如图2,过点Q作交于点P.
由(1)知,,
∴在中,,
∴,
∴.
在中,,
在中,,
∵在中,当时,,
∴小明刚好被照射到时离B点的距离为,
∴小明会被照射到.
方法2:
如图2,过点Q作交FH于点P.
与方法1同理得,得,,
∴.
在中,.
∴小明会被照射到.
(3)当时,.
当时,.
∴.
22.解:(1)ⅰ)∵ ,
又|﹣a|≥0, ≥0,
∴a=,b=﹣1,
故答案为,﹣1.
ⅱ)如图1中,有两种情形,点F坐标为:(﹣2, +1)或(2, +1).
故答案为(﹣2, +1)或(2, +1).
(2)如图2中,设BH交y轴于K.∠ABK=∠OBK=α.
∵AB∥CD,
∴∠ABO=∠OCD=2α,
∴∠ODP= (90°+2α)=45°+α.
∵∠BKO=90°﹣α,
∴∠HPD=180°﹣(90°﹣α)﹣(45°+α)=45°.
(3)如图3﹣1中,当点Q在点B左侧时,∠BAM+∠NQC=30°
如图3﹣2中,当点Q在B、C之间时,∠NQC﹣∠BAM=30°.
如图3﹣3中,当点Q在点C右侧时,∠BAM+∠NQC=60°.
23.(1)解:∵抛物线与轴交于不同的两点,
∴方程有两个不相等的实数根,
∴,
即,
∴,解得:,
又∵,
∴,
综上,且;
(2)解:∵
∴,
即,
∵该抛物线一定经过非坐标轴上的一点,
此时y的值与m无关,
∴,
解得:,
当时,,此时抛物线过点;
当时,,此时抛物线过点(舍去);
综上所述,此时点P的坐标为;
(3)解:的面积有最大值.
当时,,
解得:,
∴抛物线与x轴两个交点的横坐标分别为,
∴,
∵,
∴,
∴当时,有最大值,最大值为,
根据题意得:的面积为,
∴当最大时,的面积有最大,最大值为,此时.
24.(1)证明:连接,如图,
∵四边形是菱形,
∴,,.
∴.
∵.
∴.
∵P是垂直平分线上的点,
∴.
∴.
∴.
∴.
∴.
∵垂直平分,P在上,
∴,即点A在上.
∴直线与相切.
(2)由(1)得,则点D在上.
∵与同对,
∴.
∵四边形是菱形,
∴,.
∴.
∴.
∴.
∵,
∴在中,.
∵由(1)得,即.
∴.
∴为直角三角形,且.
∴.
又∵,
∴.
(3)设,
由(1)知:当时,直线与相切,同理:当时,直线与相切,此时,点C是切点,点E、F、C重合.
所以若点C与E不重合,可分两类讨论:
①当点E在延长线上时,
由(2)知:.
∴,即.
∵,
∴.
∴.
则.
即.
②当点E在边上时,
∵点A,E,C,D在上,
∴.
∵,
∴.
∵,
∴.
∴.
即.
又∵,
∴.
∴.
∴.
即.
综上,或.
数学·试题卷
本试卷共6页,24小题,满分120分.考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考场号和座位号填写在答题卡上.用2B铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号.将条形码粘贴在答题卡“条形码粘贴处”.
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,只上交答题卡.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各式中,能用平方差公式分解因式的是
A.a2+4b2 B.﹣x2+16y2 C.﹣a2﹣4b2 D.a﹣4b2
2.下列计算正确的是
A. B.
C. D.
3.这段时间,一个叫“学习强国”的理论学习平台火了,截止4月2号,华为官方应用市场“学习强国APP”下载量已达88300000次,请将88300000用科学记数法表示为
A.0.883×106 B.8.83×107 C.8.83×108 D.88.3×109
4.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点.过点的直线l与⊙B相交于C、D两点,则弦长是整数值的条数有
A.2个 B.3个 C.4个 D.5个
5.满足下列条件的△ABC,不是直角三角形的是
A. B.
C. D.
6.小华的妈妈去年存了一个1年期存款,年利率为3.50%,今年到期后得到利息700元,小华的妈妈去年存款的本金为
A.1000元 B.2000元 C.10000元 D.20000元
7.现有一组统计数据:,,,,,,.对于不同的,下列统计量不会发生改变的是
A.众数、中位数 B.平均数、方差
C.平均数、中位数 D.众数、方差
8.把二次函数的图象作关于原点的对称变化,所得到的图象函数式为,若,则m最小值是
A.6 B.4 C.8 D.2
9.在数轴上,点A,B分别表示实数a,b,将点A向左平移1个单位长度得到点C,若点C,B关于原点O对称,则下列结论正确的是
A.a+b=1 B.a+b=﹣1 C.a﹣b=1 D.a﹣b=﹣1
10.如图,在△ABC中,,,,将△ABC绕点A顺时针旋转得到,当点落在边上时,连接,则线段的长为
A.3 B.1 C.2 D.
(第4题) (第10题)
二、填空题:本大题共6小题,每小题4分,共24分.
11.我们把分子是1的分数叫做分数单位,有些单位分数可以拆成两个不同的分数的差,如,请用观察到的规律解方程该方程的解是 ▲ .
12.现将一把直尺和的直角三角板按如图摆放,经测量得,则 ▲ .
13.若,则 ▲ .
14.在平面直角坐标系中,点,点P的“变换点”Q的坐标定义如下:当时,,当时,,线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 ▲ .
15.如图,在△ABC中,,点在边上,,将沿折叠,的对应边交于点,连接.若,则的长为▲.
(第12题) (第15题)
16.如图1,是一种锂电池自动液压搬运物体叉车,图2是叉车侧面近似示意图.车身为四边形ABCD,,BC⊥AB,底座AB上装着两个半径为30cm的轮胎切于水平地面,AB=169cm,BC=120cm.挡货架AE上有一固定点T与AD的中点N之间由液压伸缩杆TN连接.当TN⊥AD时,TN的延长线恰好经过B点,则AD的长度是 cm;一个长方体物体准备装卸时,AE绕点A左右旋转,托物体的货叉PQ⊥AE(PQ沿着AE可上下滑动),PQ=65cm,AE=AD.当AE旋转至AF时,PQ下降到P'Q'的位置,此时F,D,C三点共线,且FQ'=52cm,则点P'到地面的离是 ▲ cm.
(第16题)
三、解答题:本大题共8小题,其中17~19题各6分,20~21题各8分,22~23题各10分,24题12分,共66分.
17.(1)解方程组:;
(2)解不等式组.
18.(1)计算∶2sin245°-6sin 30°+3tan 45°+4cos 60°.
(2)小明在用公式法解方程x2-5x=2时出现了错误,解答过程如下∶
∵a=1,b=-5,c=2,(第一步)
∴b2-4ac=(-5)2-4×1×2=17,(第二步)
∴x,(第三步)
∴ x1,x2=.(第四步)
①小明的解答过程是从第 步开始出错的,其错误的原因是
②请你写出此题正确的解答过程.
19.已知平面上A(4,4),B(2,0),C(0,6)
(1)在下面的平面直角坐标系中找出A、B、C三点,绘制出△ABC.
(2)求出△ABC的面积.
(第19题)
20.《义务教育课程方案和课程标准(2022年版)》指出,劳动课成为中小学的一门独立课程.《大中小学劳动教育指导纲要(试行)》要求初中阶段劳动时长不少于3小时,某初级中学为了解本校学生每周劳动时长,组织数学兴趣小组按下列步骤开展统计活动.
确定调查对象:
从全校1500名学生中随机抽取部分学生,进行每周劳动时长调查.
收集整理数据:
按照标准,学生每周劳动时长分为A,B,C,D四个等级,数学兴趣小组随机抽取本校部分学生进行调查,绘制成下面不完整的统计图表.
分析数据,解答问题:
(1)本次调查中:1500名学生中每名学生每周的劳动时长是______(填“总体”或“个体”);统计表中的______,______.
(2)请估算该校学生中,每周劳动时长不符合要求的人数.
(3)为更好践行劳动教育要求,结合上述数据分析,请你提出一条合理化的建议.
21.根据以下素材,探索完成任务.
探究遮阳伞下的影子长度
素材1 图1是某款自动旋转遮阳伞,伞面完全张开时张角呈,图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直.
素材2 某地区某天下午不同时间的太阳高度角(太阳光线与地面的夹角)参照表:时刻12点13点14点15点16点17点太阳高度(度)907560453015参考数据:,.
素材3 小明坐在露营椅上的高度(头顶到地面的距离)约为1米.如图2,小明坐的位置记为点Q.
问题解决
任务1 确定影子长度 某一时刻测得米,请求出此时影子的长度.
任务2 判断是否照射到 这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否会被太阳光照射到?
任务3 探究合理范围 小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算的取值范围.
22.如图,在平面直角坐标系中,线段AB的两个端点为A、B分别在y轴正半轴、x轴负半轴上,直线CD分别交x轴正半轴、y轴负半轴于点C、D,且AB∥CD.
(1)如图1,若点A(0,a)和点B(b,0)的坐标满足
ⅰ)直接写出a、b的值,a=_____,b=_____;
ⅱ)把线段AB平移,使B点的对应点E到x轴距离为1,A点的对应点F到y轴的距离为2,且EF与两坐标轴没有交点,则F点的坐标为_____;
(2)若G是CD延长线上一点DP平分∠ADG,BH平分∠ABO,BH的反向延长线交DP于P(如图2),求∠HPD的度数;
(3)若∠BAO=30°,点Q在x轴(不含点B、C)上运动,AM平分∠BAQ,QN平分∠AQC,(如图3)直接出∠BAM与∠NQC满足的数量关系.
(第22题)
23.已知抛物线与轴交于不同的两点
(1)求的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点,并求出点的坐标;
(3)当时,由(2)求出的点和点构成的的面积是否有最值?若有,求出该最值及相对应的值.
24.四边形是菱形,点O为对角线交点,边的垂直平分线交线段于点P(P不与O重合),连接,以点P为圆心,长为半径的圆交直线于点E,直线与直线交于点F,如图所示.
(1)当时,求证:直线与相切;
(2)当,时,求的度数;
(3)在菱形的边长与内角发生变化的过程中,若点C与E不重合,请探究与的数量关系.
浙江省2024年初中学业水平考试模拟演练
数学·参考答案
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B 2.B 3.B 4.B 5.A
6.D 7.A 8.D 9.A 10.C
二、填空题:本大题共6小题,每小题4分,共24分.
11. 12. 13.2
14. 15. 16. 130 77
三、解答题:本大题共8小题,其中17~19题各6分,20~21题各8分,22~23题各10分,24题12分,共66分.
17.(1)
①×2+②得,9x=9,即x=1,
把x=1代入②得:y=-1,
∴方程组的解是;
(2)
由①得,
由②得,
则不等式组的解集为.
18.解:(1)2sin245°-6sin 30°+3tan 45°+4cos 60°
=2×()2-6×+3×1+4×
=1-3+3+2
=3;
(2)①小明的解答过程是从第一步开始出错的,其错误的原因是原方程没有化成一般形式,
故答案为:一, 原方程没有化成一般形式;
②原方程变形为x -5x-2=0,
∴a=1,b=-5,c=-2,
∴b2-4ac=(-5)2-4×1×(-2)=33,
∴x,
∴x1,x2.
19.解:(1)如图△ABC即为所作:
(2):由勾股定理AB==2,
AC==2,
BC==2 ,
∵AB2+AC2=(2)2+(2)2=40,BC2=(2)2=40
∴AB2+AC2=BC2 ,
∴△ABC是直角三角形,
∴S△ABC=×2×2=10.
20.(1)解:1500名学生中每名学生每周的劳动时长是个体.
先计算D等级所占的百分比:
∴A等级所占的百分比是:
∴(人),(人).
故答案为:个体;28;80.
(2)(人),
答:估算该校学生中,每周劳动时长不符合要求的人数有600人;
(3)每周劳动时长不符合要求的占,说明学生平时劳动的时间非常少,建议学校加强劳动教育,多开展一些劳动课.
21.解:(1)如图1,过点E作于点I,过点G作于点J.
∵,,
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∵,四边形为矩形,
∴,,
∴,
∴,
在中,(米).
(2)方法1:
如图2,过点Q作交于点P.
由(1)知,,
∴在中,,
∴,
∴.
在中,,
在中,,
∵在中,当时,,
∴小明刚好被照射到时离B点的距离为,
∴小明会被照射到.
方法2:
如图2,过点Q作交FH于点P.
与方法1同理得,得,,
∴.
在中,.
∴小明会被照射到.
(3)当时,.
当时,.
∴.
22.解:(1)ⅰ)∵ ,
又|﹣a|≥0, ≥0,
∴a=,b=﹣1,
故答案为,﹣1.
ⅱ)如图1中,有两种情形,点F坐标为:(﹣2, +1)或(2, +1).
故答案为(﹣2, +1)或(2, +1).
(2)如图2中,设BH交y轴于K.∠ABK=∠OBK=α.
∵AB∥CD,
∴∠ABO=∠OCD=2α,
∴∠ODP= (90°+2α)=45°+α.
∵∠BKO=90°﹣α,
∴∠HPD=180°﹣(90°﹣α)﹣(45°+α)=45°.
(3)如图3﹣1中,当点Q在点B左侧时,∠BAM+∠NQC=30°
如图3﹣2中,当点Q在B、C之间时,∠NQC﹣∠BAM=30°.
如图3﹣3中,当点Q在点C右侧时,∠BAM+∠NQC=60°.
23.(1)解:∵抛物线与轴交于不同的两点,
∴方程有两个不相等的实数根,
∴,
即,
∴,解得:,
又∵,
∴,
综上,且;
(2)解:∵
∴,
即,
∵该抛物线一定经过非坐标轴上的一点,
此时y的值与m无关,
∴,
解得:,
当时,,此时抛物线过点;
当时,,此时抛物线过点(舍去);
综上所述,此时点P的坐标为;
(3)解:的面积有最大值.
当时,,
解得:,
∴抛物线与x轴两个交点的横坐标分别为,
∴,
∵,
∴,
∴当时,有最大值,最大值为,
根据题意得:的面积为,
∴当最大时,的面积有最大,最大值为,此时.
24.(1)证明:连接,如图,
∵四边形是菱形,
∴,,.
∴.
∵.
∴.
∵P是垂直平分线上的点,
∴.
∴.
∴.
∴.
∴.
∵垂直平分,P在上,
∴,即点A在上.
∴直线与相切.
(2)由(1)得,则点D在上.
∵与同对,
∴.
∵四边形是菱形,
∴,.
∴.
∴.
∴.
∵,
∴在中,.
∵由(1)得,即.
∴.
∴为直角三角形,且.
∴.
又∵,
∴.
(3)设,
由(1)知:当时,直线与相切,同理:当时,直线与相切,此时,点C是切点,点E、F、C重合.
所以若点C与E不重合,可分两类讨论:
①当点E在延长线上时,
由(2)知:.
∴,即.
∵,
∴.
∴.
则.
即.
②当点E在边上时,
∵点A,E,C,D在上,
∴.
∵,
∴.
∵,
∴.
∴.
即.
又∵,
∴.
∴.
∴.
即.
综上,或.
同课章节目录
