空间向量与立体几何解答题专项特训2023-2024学年数学人教A版选择性必修第一册(含答案)
文档属性
| 名称 | 空间向量与立体几何解答题专项特训2023-2024学年数学人教A版选择性必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 20:51:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
空间向量与立体几何解答题专项特训2023-2024学年数学人教A版选择性必修第一册
1.如图,在三棱锥 P-ABC中,平面 PAB⊥平面ABC,AB=4,BC=2,AC=PA=PB=2,D,E分别为PC,PA的中点.
(1)证明:平面 BCE⊥平面 PAB.
(2)求平面 PBC与平面BDE 的夹角的余弦值.
2.在四棱锥中,底面ABCD为直角梯形,BCAD,∠ADC=90°,,E为线段AD的中点.底面ABCD,点F是棱长PC的中点,平面BEF与棱PD相交于点G.
(1)求证:BEFG;
(2)若PC与AB所成的角为,求直线PB与平面BEF所成角的正弦值.
3.如图甲是由梯形ABCD和正三角形CDE组成的一个平面图形,其中BC∥AD,AB⊥AD,AD=2BC=2AB=2,将△CDE沿CD折起使点E到达点P的位置(如图乙),使二面角P﹣CD﹣B为直二面角.
(1)证明:AC⊥PD;
(2)若平面PCD与平面PAB的交线为l,求l与平面PAD所成角的正弦值.
4.已知在多面体中,,,,,,且平面平面.
(1)设点为线段的中点,试证明平面;
(2)与平面所成的角为,求二面角的余弦值.
5.如图,在四边形ABCD中(如图1),,,,,F分别是边BD,CD上的点,将沿BC翻折,将沿EF翻折,使得点与点重合(记为点),且平面平面BCFE(如图2)
(1)求证:;
(2)求二面角的余弦值.
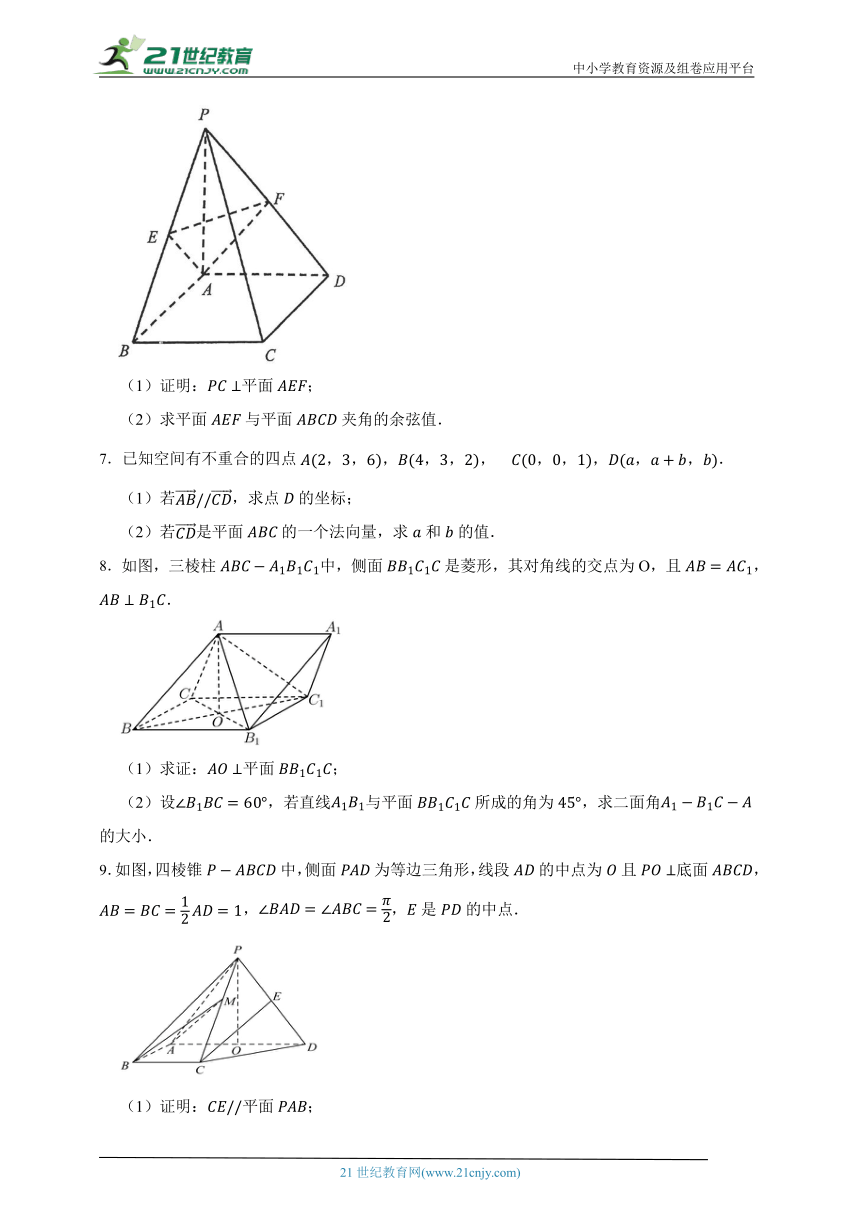
6.如图,在四棱锥中,底面为正方形,侧棱底面,且,点分别为的中点.
(1)证明:平面;
(2)求平面与平面夹角的余弦值.
7.已知空间有不重合的四点.
(1)若,求点的坐标;
(2)若是平面的一个法向量,求和的值.
8.如图,三棱柱中,侧面是菱形,其对角线的交点为O,且,.
(1)求证:平面;
(2)设,若直线与平面所成的角为,求二面角的大小.
9.如图,四棱锥中,侧面为等边三角形,线段的中点为且底面,,,是的中点.
(1)证明:平面;
(2)点在棱上,且直线与底面所成角为,求平面与平面夹角的余弦值;
(3)在的条件下,求点到平面的距离.
10.已知空间三点,,,设,.
(1)求;
(2)与互相垂直,求实数的值.
11.如图,在直棱柱中,,E,F分别是棱,上的动点,且.
(1)证明:.
(2)当三棱锥的体积取得最大值时,求平面与平面的夹角的余弦值.
12.如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,,AP⊥平面ABCD,,点M、N分别为线段BC和PD的中点.
(1)求证:AN⊥平面PDM;
(2)求平面PDM与平面PDC夹角的正弦值;
(3)在线段PC(不包括端点)上是否存在一点E,使得直线BE与平面PDC所成角的正弦值为,若存在,求出线身PE的长:若不存在,请说明理由.
13.如图, 四边形 为平行四边形, 点在上,, 且.以为折痕把折起, 使点到达点的位置, 且.
(1)求证: 平面;
(2)若直线 与平面所成角的正弦值为,求点到平面的距离.
14.如图,在直三棱柱中,,.
(1)求证:;
(2)求点到平面的距离.
15.如下图,在四棱锥中,平面平面ABCD,平面平面ABCD,又.
(1)求点到平面的距离;
(2)设,,,平面PBC与平面PCD夹角的余弦值为,求BC的长.
16.在如图所示的五面体中,共面,是正三角形,四边形为菱形,,平面,,点为中点.
(1)在直线上是否存在一点,使得平面平面,请说明理由;
(2)当,求平面与平面所成二面角的正弦值.
答案解析部分
1.【答案】(1)解:证明:因为AB=4,BC=2,AC=2 ,所以
所以AB⊥BC.
因为平面PAB⊥平面ABC,且平面PAB∩平面ABC=AB,所以BC⊥平面PAB.
又BC 平面BCE,所以平面BCE⊥平面PAB
(2)解:取 AB的中点O,连接 PO.以O为坐标原点, 的方向为x轴的正方向建立如图所示的空间直角坐标系,
其中y轴与BC 平行,则P(0,0,4),A(-2,0,0),B(2,0,0),
E(-1,0,2),C(2,2,0),D(1,1,2)
设平面 BDE的法向量为
则
令z=3,得m=(2,-4,3).
设平面 PBC 的法向量为
则
令 ,得n=(2,0,1).
因为
所以平面 PBC 与平面 BDE 的夹角的余弦值为
2.【答案】(1)证明:因为E为AD中点,
所以.
又因为BC=1,所以DE=BC.在梯形ABCD中,DEBC,
所以四边形BCDE为平行四边形.所以BECD.
又因为平面PCD,且CD 平面PCD,
所以BE平面PCD.
因为BE 平面BEF,平面BEF∩平面,
所以BEFG.
(2)解:因为PE⊥平面ABCD,且AE,BE 平面ABCD,
所以PE⊥AE,且PE⊥BE.
因为四边形BCDE为平行四边形,,
所以AE⊥BE.
以E为坐标原点,如图建立空间直角坐标系E﹣xyz.
则.
设,
所以,.
因为PC与AB所成角为,
所以.
所以.
则,.
所以,,.
设平面BEF的法向量为,
则即
令x=6,则,
所以.
所以.
所以直线PB与平面BEF的所成角的正弦值为.
3.【答案】(1)证明:取AD中点为F,连接AC,CF,由AD=2BC得AF∥BC且AF=BC.
∴四边形ABCF为平行四边形,
∴CF=AF=DF,
∴AC⊥CD,
又因为二面角P﹣CD﹣B为直二面角,且平面PCD 平面ABCD=CD,
∴AC⊥平面PCD,因为PD 平面PCD,
所以AC⊥PD.
(2)解:如图,延长AB和DC交于点G,连接GP,则GP为平面PCD与平面PAB的交线l,
取CD中点为O,连接OF,OP,
∵OP⊥AC,OF∥AC,
∴OP⊥OF,OF⊥CD,OP⊥CD,
以O为坐标原点,OF,OD,OP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则,,,,
所以,,,
设平面PAD的法向量为,
则,
令c=1,得,
设l与平面PAD的所成角为θ,
则,
因为,
即l与平面PAD所成角的正弦值为.
4.【答案】(1)证明:取的中点,连接,.
在中,.
平面平面,平面平面,平面,
平面.
,分别为,的中点,,且.
又,,,且.
四边形为平行四边形
,平面.
(2)解:平面,,
以为原点,所在直线为轴,过点与平行的直线为轴,所在直线为轴,建立空间直角坐标系.
则,,.
平面,直线与平面所成的角为.
..
可取平面的一个法向量为,
设平面的法向量为,
,,
则,取,则,,
,
,
二面角的余弦值为.
5.【答案】(1)证明:∵平面平面,
平面平面BCFE,又∵平面BCFE,且
∴平面PBC,且平面,∴
(2)解:取BC中点,连接PO,
∵,∴
∵平面平面,平面平面,平面
∴平面BCFE
以为原点,CB,CF所在直线分别为轴,轴建立如图所示的空间直角坐标系,
设,则,,,设,
由得,解得,所以,
设,由得,解得,
∴,则,,
平面BEF的一个法向量,设平面PEF的一个法向量,
,令,得,
设二面角的平面角为,易知为锐角,则,
∴二面角的余弦值为.
6.【答案】(1)证明:因为底面,所以,①
又因为为正方形,所以,②
由①②可得平面,
所以,③
又因为,点为的中点,所以.④
由③④可得平面,所以.
同理可得,所以平面.
(2)解:如图,以点为坐标原点,为轴正方向,为轴正方向,为轴正方向,建立空间直角坐标系,设,则各点坐标分别为
.
由(Ⅰ)可知是平面的一个法向量,记为,
又平面的一个法向量为.
所以平面与平面夹角的余弦值等于.
7.【答案】(1)解:,
因为,故存在实数,使得,
即,
故解得
点的坐标为;
(2)解:因为是平面的一个法向量,故,
又,,
故,
解得.
8.【答案】(1)证明:证明:四边形是菱形,,
,且,平面,
平面,因为平面,,
,是的中点,,
又,平面,所以平面.
(2)解:,
直线与平面的所成角等于直线与平面的所成角,
平面,
直线与平面的所成角为,即,
设菱形的边长为2,则在等边中,,,
在等腰直角中,,
以为原点建立空间直角坐标系,则,,,,
,,
设平面的一个法向量为,,,
则,取,得,0,,
平面的一个法向量为,
所以,显然二面角为锐二面角,
二面角的大小为.
9.【答案】(1)解:连接,因为,所以四边形为平行四边形,
所以,所以,以,,分别为,,轴建立空间直角坐标系,
则,,,,,
,,,
设平面的一个法向量为,
则,则,令,,
平面的一个法向量,
,则,又平面,所以平面.
(2)解:,设,则,
因为点在棱上,所以,,
即,
所以,所以,
平面的法向量为,
因为直线与底面所成角为,所以,
,解得,所以,
设平面的法向量为,
则,即,令,则,
所以,所以平面与平面夹角的余弦值
(3)解:,点到平面的距离
10.【答案】(1)解:由题设,,
所以;
(2)解:由,,而,
所以,
可得或.
11.【答案】(1)证明:由题意知在直棱柱中,,可得,
所以,即,,两两垂直,如图,建立空间直角坐标系.
不妨设,,则,,,,,,
所以,,
可得,
所以,
即.
(2)解:,
当且仅当,即时,有最大值,
此时E,F分别为,的中点,,,所以,,所以可取平面的一个法向量为.
,,所以可取平面的一个法向量为
设平面与平面的夹角为,则,
所以平面与平面的夹角的余弦值为
12.【答案】(1)证明:方法一:∵,且,
∴BM∥AD,且BM=AD,
∴四边形ADMB是平行四边形,
∴,
∵,则AD⊥DM,
∵AP⊥平面ABCD,平面ABCD,
∴AP⊥DM,又,
∴DM⊥平面PAD,又平面PAD,
∴DM⊥AN,
∵,N是PD的中点,
∴PD⊥AN,又,、平面PDM,
∴AN⊥平面PDM;
方法二:以A为原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则,,,,,,.
则,,.
设平面PDM的法向量为,
则,即,取,则,,则,
∴,则,
∴AN⊥平面PDM;
(2)解:,,设平面PDC的法向量为,
则,则,取,则,,则,
由(1)知平面PDM的一个法向量为,
设平面PDM与平面PDC的夹角为,
则,
∴,
∴平面PDM与平面PDC夹角的正弦值为;
(3)解:假设存在点E,设,
,,,
则,
设直线BE与平面PDC所成角为,
由(2)知平面PDC的一个法向量为,
则,
化简得,即,
∵,∴,故,
∵,则,
∴,
∴线段PE的长为.
13.【答案】(1)证明:由题 , 所以,
又 平面平面.
因为 平面平面, 所以,
因为 , 所以,
因为 , 所以在中,
由余弦定理得 ,
所以 , 所以由勾股定理逆定理得,
因为 平面, 所以平面
(2)解:以 为原点,所在的直线为轴, 在平面过点作的垂线为轴,
所在的直线为轴, 建立空间直线坐标系设,
则 ,
平面 的一个法向量,由直线与平面所成角的正弦值为,
所以 , 解得(负值舍去),
设平面 的法向量, 则,
取 , 得,故点到平面的距离.
14.【答案】(1)证明:建立直角坐标系,其中为坐标原点.
依题意得,
因为,所以.
(2)解:设是平面的法向量,
由得
所以,令,则,
因为,所以到平面的距离为
15.【答案】(1)解:如图,在平面ABCD中取一点E,并过点E作直线,
,因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
,所以,又,
所以.同理,又,,
所以及,点P到平面ABCD的距离为.
(2)解:如图所示,以A点为原点,分别以AD,AB, AP为x轴,y轴,z轴,建立空间直角坐标系.
则B(0,1,0),D(2,0,0),P(0,0,2),
∴,,设,则
,.
设平面的法向量为,则
则,令,得.
同理可得平面的法向量为.
由题意知,解得,
所以BC的长为.
16.【答案】(1)解:在直线上存在一点,使得平面平面,理由如下:
取的中点,连接,
由点为中点,得,平面,平面,则平面,
又平面,平面,平面平面,则,
四边形是菱形,则,于是四边形是平行四边形,
则,平面,平面,则平面,
而平面,所以平面平面.
(2)解:四边形为菱形,,则为正三角形,,
在中,,由余弦定理知,
取中点,连接,而是正三角形,则,
显然,即,又,即直线两两垂直,
以为原点,直线分别为轴建立空间直角坐标系,如图,
则,,,
由,得,则,,
设平面的法向量为,则,令,得,
设平面的法向量为,则,令,得,
设平面与平面所成二面角为,,
所以平面与平面所成二面角的正弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
空间向量与立体几何解答题专项特训2023-2024学年数学人教A版选择性必修第一册
1.如图,在三棱锥 P-ABC中,平面 PAB⊥平面ABC,AB=4,BC=2,AC=PA=PB=2,D,E分别为PC,PA的中点.
(1)证明:平面 BCE⊥平面 PAB.
(2)求平面 PBC与平面BDE 的夹角的余弦值.
2.在四棱锥中,底面ABCD为直角梯形,BCAD,∠ADC=90°,,E为线段AD的中点.底面ABCD,点F是棱长PC的中点,平面BEF与棱PD相交于点G.
(1)求证:BEFG;
(2)若PC与AB所成的角为,求直线PB与平面BEF所成角的正弦值.
3.如图甲是由梯形ABCD和正三角形CDE组成的一个平面图形,其中BC∥AD,AB⊥AD,AD=2BC=2AB=2,将△CDE沿CD折起使点E到达点P的位置(如图乙),使二面角P﹣CD﹣B为直二面角.
(1)证明:AC⊥PD;
(2)若平面PCD与平面PAB的交线为l,求l与平面PAD所成角的正弦值.
4.已知在多面体中,,,,,,且平面平面.
(1)设点为线段的中点,试证明平面;
(2)与平面所成的角为,求二面角的余弦值.
5.如图,在四边形ABCD中(如图1),,,,,F分别是边BD,CD上的点,将沿BC翻折,将沿EF翻折,使得点与点重合(记为点),且平面平面BCFE(如图2)
(1)求证:;
(2)求二面角的余弦值.
6.如图,在四棱锥中,底面为正方形,侧棱底面,且,点分别为的中点.
(1)证明:平面;
(2)求平面与平面夹角的余弦值.
7.已知空间有不重合的四点.
(1)若,求点的坐标;
(2)若是平面的一个法向量,求和的值.
8.如图,三棱柱中,侧面是菱形,其对角线的交点为O,且,.
(1)求证:平面;
(2)设,若直线与平面所成的角为,求二面角的大小.
9.如图,四棱锥中,侧面为等边三角形,线段的中点为且底面,,,是的中点.
(1)证明:平面;
(2)点在棱上,且直线与底面所成角为,求平面与平面夹角的余弦值;
(3)在的条件下,求点到平面的距离.
10.已知空间三点,,,设,.
(1)求;
(2)与互相垂直,求实数的值.
11.如图,在直棱柱中,,E,F分别是棱,上的动点,且.
(1)证明:.
(2)当三棱锥的体积取得最大值时,求平面与平面的夹角的余弦值.
12.如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,,AP⊥平面ABCD,,点M、N分别为线段BC和PD的中点.
(1)求证:AN⊥平面PDM;
(2)求平面PDM与平面PDC夹角的正弦值;
(3)在线段PC(不包括端点)上是否存在一点E,使得直线BE与平面PDC所成角的正弦值为,若存在,求出线身PE的长:若不存在,请说明理由.
13.如图, 四边形 为平行四边形, 点在上,, 且.以为折痕把折起, 使点到达点的位置, 且.
(1)求证: 平面;
(2)若直线 与平面所成角的正弦值为,求点到平面的距离.
14.如图,在直三棱柱中,,.
(1)求证:;
(2)求点到平面的距离.
15.如下图,在四棱锥中,平面平面ABCD,平面平面ABCD,又.
(1)求点到平面的距离;
(2)设,,,平面PBC与平面PCD夹角的余弦值为,求BC的长.
16.在如图所示的五面体中,共面,是正三角形,四边形为菱形,,平面,,点为中点.
(1)在直线上是否存在一点,使得平面平面,请说明理由;
(2)当,求平面与平面所成二面角的正弦值.
答案解析部分
1.【答案】(1)解:证明:因为AB=4,BC=2,AC=2 ,所以
所以AB⊥BC.
因为平面PAB⊥平面ABC,且平面PAB∩平面ABC=AB,所以BC⊥平面PAB.
又BC 平面BCE,所以平面BCE⊥平面PAB
(2)解:取 AB的中点O,连接 PO.以O为坐标原点, 的方向为x轴的正方向建立如图所示的空间直角坐标系,
其中y轴与BC 平行,则P(0,0,4),A(-2,0,0),B(2,0,0),
E(-1,0,2),C(2,2,0),D(1,1,2)
设平面 BDE的法向量为
则
令z=3,得m=(2,-4,3).
设平面 PBC 的法向量为
则
令 ,得n=(2,0,1).
因为
所以平面 PBC 与平面 BDE 的夹角的余弦值为
2.【答案】(1)证明:因为E为AD中点,
所以.
又因为BC=1,所以DE=BC.在梯形ABCD中,DEBC,
所以四边形BCDE为平行四边形.所以BECD.
又因为平面PCD,且CD 平面PCD,
所以BE平面PCD.
因为BE 平面BEF,平面BEF∩平面,
所以BEFG.
(2)解:因为PE⊥平面ABCD,且AE,BE 平面ABCD,
所以PE⊥AE,且PE⊥BE.
因为四边形BCDE为平行四边形,,
所以AE⊥BE.
以E为坐标原点,如图建立空间直角坐标系E﹣xyz.
则.
设,
所以,.
因为PC与AB所成角为,
所以.
所以.
则,.
所以,,.
设平面BEF的法向量为,
则即
令x=6,则,
所以.
所以.
所以直线PB与平面BEF的所成角的正弦值为.
3.【答案】(1)证明:取AD中点为F,连接AC,CF,由AD=2BC得AF∥BC且AF=BC.
∴四边形ABCF为平行四边形,
∴CF=AF=DF,
∴AC⊥CD,
又因为二面角P﹣CD﹣B为直二面角,且平面PCD 平面ABCD=CD,
∴AC⊥平面PCD,因为PD 平面PCD,
所以AC⊥PD.
(2)解:如图,延长AB和DC交于点G,连接GP,则GP为平面PCD与平面PAB的交线l,
取CD中点为O,连接OF,OP,
∵OP⊥AC,OF∥AC,
∴OP⊥OF,OF⊥CD,OP⊥CD,
以O为坐标原点,OF,OD,OP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则,,,,
所以,,,
设平面PAD的法向量为,
则,
令c=1,得,
设l与平面PAD的所成角为θ,
则,
因为,
即l与平面PAD所成角的正弦值为.
4.【答案】(1)证明:取的中点,连接,.
在中,.
平面平面,平面平面,平面,
平面.
,分别为,的中点,,且.
又,,,且.
四边形为平行四边形
,平面.
(2)解:平面,,
以为原点,所在直线为轴,过点与平行的直线为轴,所在直线为轴,建立空间直角坐标系.
则,,.
平面,直线与平面所成的角为.
..
可取平面的一个法向量为,
设平面的法向量为,
,,
则,取,则,,
,
,
二面角的余弦值为.
5.【答案】(1)证明:∵平面平面,
平面平面BCFE,又∵平面BCFE,且
∴平面PBC,且平面,∴
(2)解:取BC中点,连接PO,
∵,∴
∵平面平面,平面平面,平面
∴平面BCFE
以为原点,CB,CF所在直线分别为轴,轴建立如图所示的空间直角坐标系,
设,则,,,设,
由得,解得,所以,
设,由得,解得,
∴,则,,
平面BEF的一个法向量,设平面PEF的一个法向量,
,令,得,
设二面角的平面角为,易知为锐角,则,
∴二面角的余弦值为.
6.【答案】(1)证明:因为底面,所以,①
又因为为正方形,所以,②
由①②可得平面,
所以,③
又因为,点为的中点,所以.④
由③④可得平面,所以.
同理可得,所以平面.
(2)解:如图,以点为坐标原点,为轴正方向,为轴正方向,为轴正方向,建立空间直角坐标系,设,则各点坐标分别为
.
由(Ⅰ)可知是平面的一个法向量,记为,
又平面的一个法向量为.
所以平面与平面夹角的余弦值等于.
7.【答案】(1)解:,
因为,故存在实数,使得,
即,
故解得
点的坐标为;
(2)解:因为是平面的一个法向量,故,
又,,
故,
解得.
8.【答案】(1)证明:证明:四边形是菱形,,
,且,平面,
平面,因为平面,,
,是的中点,,
又,平面,所以平面.
(2)解:,
直线与平面的所成角等于直线与平面的所成角,
平面,
直线与平面的所成角为,即,
设菱形的边长为2,则在等边中,,,
在等腰直角中,,
以为原点建立空间直角坐标系,则,,,,
,,
设平面的一个法向量为,,,
则,取,得,0,,
平面的一个法向量为,
所以,显然二面角为锐二面角,
二面角的大小为.
9.【答案】(1)解:连接,因为,所以四边形为平行四边形,
所以,所以,以,,分别为,,轴建立空间直角坐标系,
则,,,,,
,,,
设平面的一个法向量为,
则,则,令,,
平面的一个法向量,
,则,又平面,所以平面.
(2)解:,设,则,
因为点在棱上,所以,,
即,
所以,所以,
平面的法向量为,
因为直线与底面所成角为,所以,
,解得,所以,
设平面的法向量为,
则,即,令,则,
所以,所以平面与平面夹角的余弦值
(3)解:,点到平面的距离
10.【答案】(1)解:由题设,,
所以;
(2)解:由,,而,
所以,
可得或.
11.【答案】(1)证明:由题意知在直棱柱中,,可得,
所以,即,,两两垂直,如图,建立空间直角坐标系.
不妨设,,则,,,,,,
所以,,
可得,
所以,
即.
(2)解:,
当且仅当,即时,有最大值,
此时E,F分别为,的中点,,,所以,,所以可取平面的一个法向量为.
,,所以可取平面的一个法向量为
设平面与平面的夹角为,则,
所以平面与平面的夹角的余弦值为
12.【答案】(1)证明:方法一:∵,且,
∴BM∥AD,且BM=AD,
∴四边形ADMB是平行四边形,
∴,
∵,则AD⊥DM,
∵AP⊥平面ABCD,平面ABCD,
∴AP⊥DM,又,
∴DM⊥平面PAD,又平面PAD,
∴DM⊥AN,
∵,N是PD的中点,
∴PD⊥AN,又,、平面PDM,
∴AN⊥平面PDM;
方法二:以A为原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则,,,,,,.
则,,.
设平面PDM的法向量为,
则,即,取,则,,则,
∴,则,
∴AN⊥平面PDM;
(2)解:,,设平面PDC的法向量为,
则,则,取,则,,则,
由(1)知平面PDM的一个法向量为,
设平面PDM与平面PDC的夹角为,
则,
∴,
∴平面PDM与平面PDC夹角的正弦值为;
(3)解:假设存在点E,设,
,,,
则,
设直线BE与平面PDC所成角为,
由(2)知平面PDC的一个法向量为,
则,
化简得,即,
∵,∴,故,
∵,则,
∴,
∴线段PE的长为.
13.【答案】(1)证明:由题 , 所以,
又 平面平面.
因为 平面平面, 所以,
因为 , 所以,
因为 , 所以在中,
由余弦定理得 ,
所以 , 所以由勾股定理逆定理得,
因为 平面, 所以平面
(2)解:以 为原点,所在的直线为轴, 在平面过点作的垂线为轴,
所在的直线为轴, 建立空间直线坐标系设,
则 ,
平面 的一个法向量,由直线与平面所成角的正弦值为,
所以 , 解得(负值舍去),
设平面 的法向量, 则,
取 , 得,故点到平面的距离.
14.【答案】(1)证明:建立直角坐标系,其中为坐标原点.
依题意得,
因为,所以.
(2)解:设是平面的法向量,
由得
所以,令,则,
因为,所以到平面的距离为
15.【答案】(1)解:如图,在平面ABCD中取一点E,并过点E作直线,
,因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
,所以,又,
所以.同理,又,,
所以及,点P到平面ABCD的距离为.
(2)解:如图所示,以A点为原点,分别以AD,AB, AP为x轴,y轴,z轴,建立空间直角坐标系.
则B(0,1,0),D(2,0,0),P(0,0,2),
∴,,设,则
,.
设平面的法向量为,则
则,令,得.
同理可得平面的法向量为.
由题意知,解得,
所以BC的长为.
16.【答案】(1)解:在直线上存在一点,使得平面平面,理由如下:
取的中点,连接,
由点为中点,得,平面,平面,则平面,
又平面,平面,平面平面,则,
四边形是菱形,则,于是四边形是平行四边形,
则,平面,平面,则平面,
而平面,所以平面平面.
(2)解:四边形为菱形,,则为正三角形,,
在中,,由余弦定理知,
取中点,连接,而是正三角形,则,
显然,即,又,即直线两两垂直,
以为原点,直线分别为轴建立空间直角坐标系,如图,
则,,,
由,得,则,,
设平面的法向量为,则,令,得,
设平面的法向量为,则,令,得,
设平面与平面所成二面角为,,
所以平面与平面所成二面角的正弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
