第二十六章 反比例函数综合自检卷(含解析)
文档属性
| 名称 | 第二十六章 反比例函数综合自检卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 10:15:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年人教版数学九年级下册第二十六章反比例函数综合自检卷
一、单选题
1.已知反比例函数的图象具有下列特征:在每个象限内,的值随的增大而增大,那么的取值范围是( )
A. B. C. D.
2.已知反比例函数图像经过点,下列说法中不正确的是( )
A.该函数图象在第二、四象限 B.点在该函数图象上
C.随的增大而增大 D.当时,
3.已知:平面直角坐标系中,点的坐标为,点关于原点对称的点恰好落在反比例函数的图象上,则( )
A.6 B. C.4 D.9
4.若点,,都在反比例函数的图象上,则( )
A. B.
C. D.
5.下列函数中,当时,y随x的增大而减小的是( )
A. B. C. D.
6.已知一次函数和反比例函数的图象如图所示,则二次函数的图象大致可能是( )
A. B. C. D.
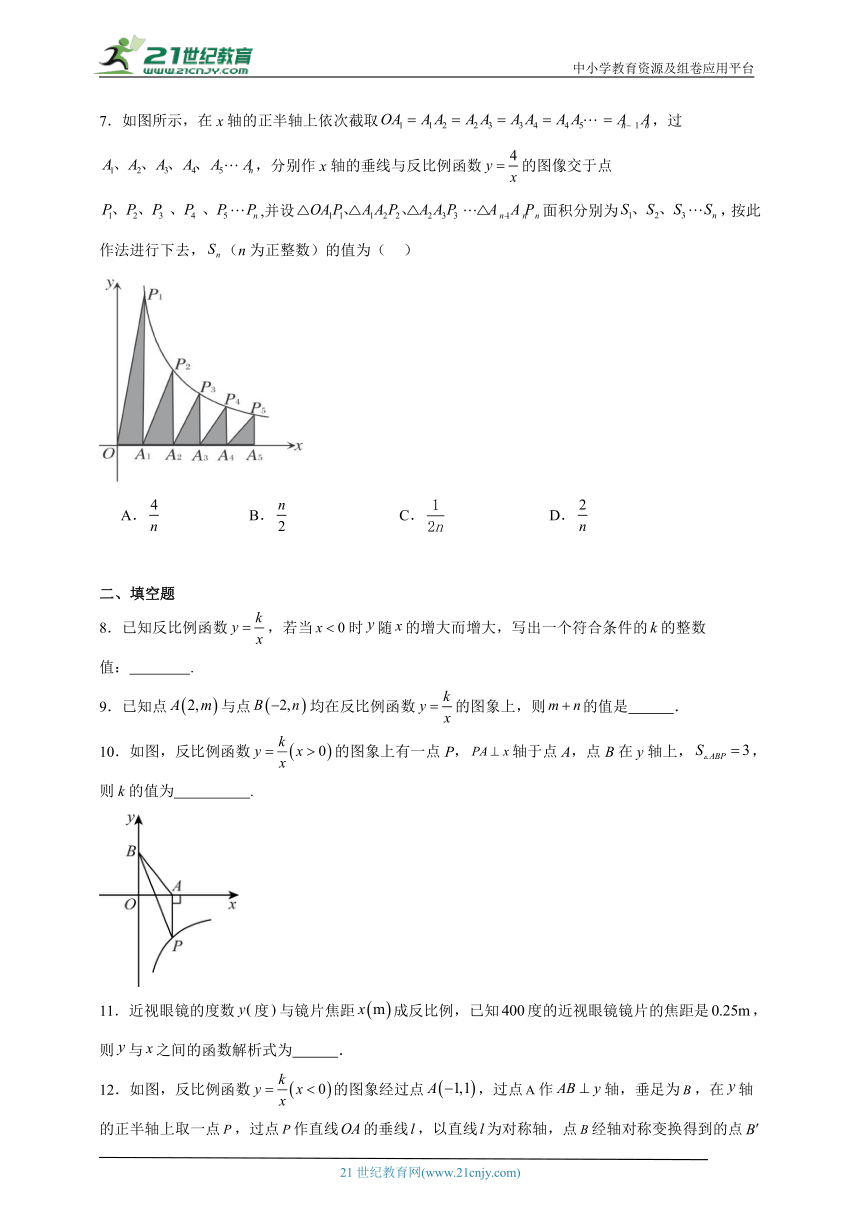
7.如图所示,在x轴的正半轴上依次截取,过,分别作x轴的垂线与反比例函数的图像交于点,并设面积分别为,按此作法进行下去,(n为正整数)的值为( )
A. B. C. D.
二、填空题
8.已知反比例函数,若当时随的增大而增大,写出一个符合条件的的整数值: .
9.已知点与点均在反比例函数的图象上,则的值是 .
10.如图,反比例函数的图象上有一点P,轴于点A,点B在y轴上,,则k的值为 .
11.近视眼镜的度数度与镜片焦距成反比例,已知度的近视眼镜镜片的焦距是,则与之间的函数解析式为 .
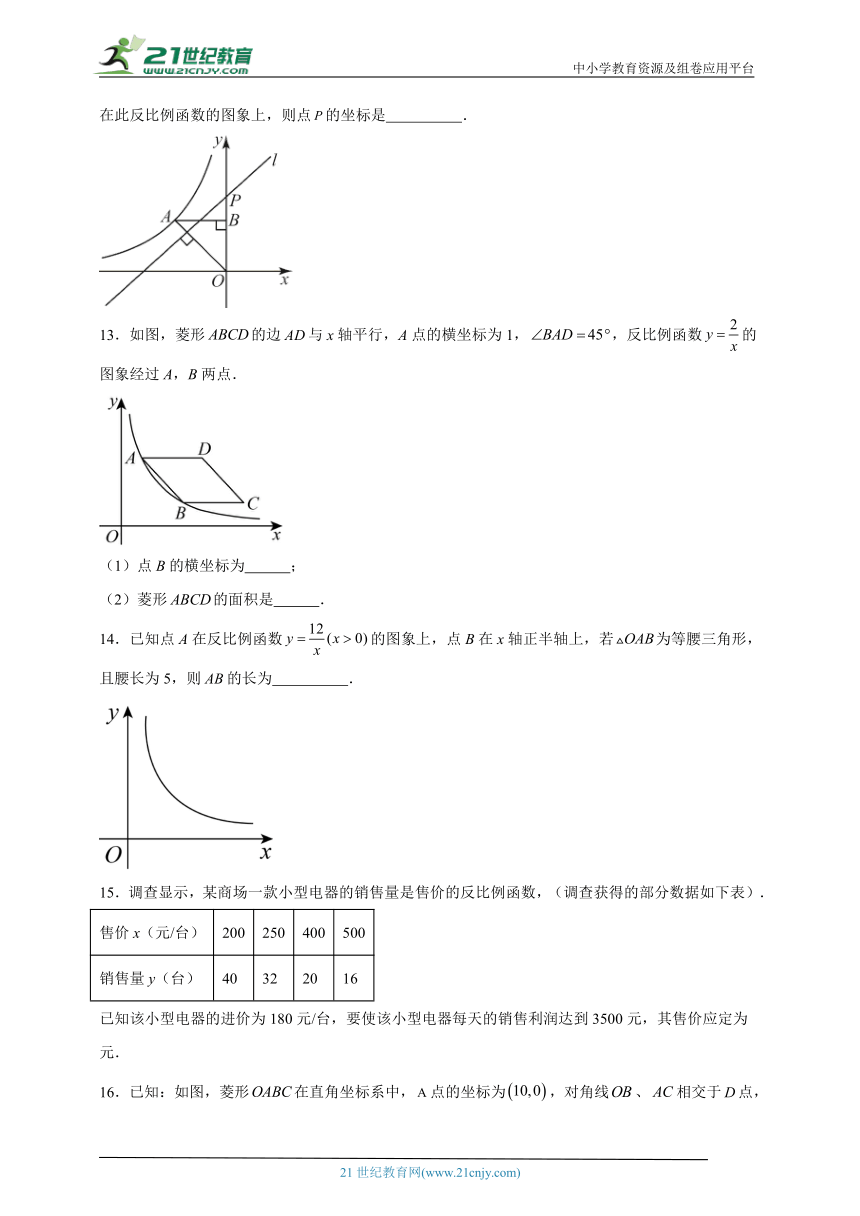
12.如图,反比例函数的图象经过点,过点作轴,垂足为,在轴的正半轴上取一点,过点作直线的垂线,以直线为对称轴,点经轴对称变换得到的点在此反比例函数的图象上,则点的坐标是 .
13.如图,菱形的边与x轴平行,A点的横坐标为1,,反比例函数的图象经过A,B两点.
(1)点B的横坐标为 ;
(2)菱形的面积是 .
14.已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为 .
15.调查显示,某商场一款小型电器的销售量是售价的反比例函数,(调查获得的部分数据如下表).
售价x(元/台) 200 250 400 500
销售量y(台) 40 32 20 16
已知该小型电器的进价为180元/台,要使该小型电器每天的销售利润达到3500元,其售价应定为 元.
16.已知:如图,菱形在直角坐标系中,点的坐标为,对角线、相交于点,双曲线经过点,交的延长线于点,且,有下列四个结论,其中正确的结论是 .
双曲线的解析式为;;点的坐标是;.
三、解答题
17.已知反比例函数图象经过.
(1)求的值;
(2)若点,是反比例函数图象上两点,试比较,大小.
18.某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示.
(1)写出压强关于木板面积的函数解析式;
(2)当木板面积为时,木板对地面的压强是多少?
19.如图,一次函数的图象与反比例函数(为常数且)的图象交于,两点,与轴交于点.
(1)求反比例函数的表达式与点坐标;
(2)请直接写出不等式的解集;
(3)若点是线段上的一个动点,作轴交反比例函数的图象于点,则的面积的最大值为______.
20.已知反比例函数的图象的一支如图所示,它与直线交于点,.
(1)在图中,补画该反比例函数图象的另一支,并求的值;
(2)当时,求函数值的取值范围;
(3)观察图象,直接写出当时,自变量的取值范围.
21.如图:等腰直角放置在直角坐标系中,,,点A在x轴上,点B的坐标是,点C在第一象限内,作轴.
(1)求证:;
(2)若点C恰好在曲线上,求点C的坐标
22.某蔬菜生产基地用装有恒温系统的大棚栽培一种新品.如图,这是某天恒温系统从开始到关闭及关闭后,大棚里的温度随时间变化的函数图象,其中段是恒温阶段,段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求的值.
(2)求恒温系统在这一天内保持大棚内温度不低于的时间有多长.
参考答案:
1.C
【分析】本题主要考查了反比例函数图象的性质,解题的关键是熟练掌握反比例函数的性质:当时,图象在一、三象限,在每一象限内,y随x的增大而减小;当时,图象在二、四象限,在每一象限内,y随x的增大而增大.
【详解】解:∵反比例函数在每个象限内,的值随的增大而增大,
∴,
∴,
故选:C.
2.C
【分析】本题主要考查了反比例函数的图像和性质,确定反比例函数解析式中的k是解题的关键.
先确定反比例函数解析式,再根据反比例函数的性质逐项分析即可解答.
【详解】解:把点代入反比例函数可得,,即.
A、该函数的图像在第二、四象限,故A选项正确,不符合题意;
B、将点代入解析式,满足解析式,故B选项正确,不符合题意;
C、在每个象限内,y随着x的增大而增大,故C选项错误,符合题意;
D、当时,,故D选项正确,不符合题意.
故选C.
3.B
【分析】本题主要考查原点对称的点的坐标特征,反比例函数上点的坐标特征,把代入解析式即可,熟练掌握待定系数法是解题的关键.
【详解】与点关于原点对称,点的坐标为
点恰好落在反比例函数的图象上
故选:B.
4.B
【分析】本题主要考查反比例函数的图像和性质,熟练掌握反比例函数的图像和性质是解题的关键.根据解析式求出函数值比较大小即可.
【详解】解:,,都在反比例函数的图象上,
,
,
,
故,
故选B.
5.D
【分析】此题主要考查了反比例函数的性质、二次函数的性质,正确掌握相关函数增减性是解题关键.直接利用反比例函数的性质、二次函数的性质分别判断得出答案.
【详解】解:A、,当时,y随x的增大而增大,不合题意;
B、,开口方向向下,对称轴为直线,所以当时,y随x的增大而增大,当时,y随x的增大而减小,不合题意;
C、,开口方向向下,对称轴为直线,当时,y随x的增大而增大,当时,y随x的增大而减小,不合题意;
D、,当时,y随x的增大而减小,符合题意;
故选:D.
6.B
【分析】本题考查了一次函数的图象、反比例函数的图象以及二次函数的图象,解题的关键是根据一次函数与反比例函数的图象找出、、的正负.根据一次函数与反比例函数图象找出、、的正负,再根据抛物线的对称轴为,得出二次函数对称轴在轴右侧,比对四个选项的函数图象即可得出结论.
【详解】解:∵一次函数图象过第一、二、四象限,
∴,
∴,
∴二次函数开口向下,对称轴在轴右侧;
∵反比例函数的图象在第一、三象限,
∴,
∴与轴交点在轴上方,
满足上述条件的函数图象只有选项B.
故选:B.
7.D
【分析】主要考查了反比例函数中k的几何意义,根据反比例函数中k的几何意义再结合图象即可解答.
【详解】解:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,.
又因为,
所以,,,,,
,
依此类推:的值为.
故选:D.
8.(答案不唯一)
【分析】本题考查反比例函数的图像与性质,涉及反比例函数图像增减性与常数符号的关系,熟记当时随的增大而增大,则即可得到答案,熟记反比例函数图像增减性与常数符号的关系是解决问题的关键.
【详解】解:反比例函数,当时随的增大而增大,
,
一个符合条件的的整数值可取(写出任意负整数即可),
故答案为:(答案不唯一).
9.0
【分析】本题主要考查了反比例函数图象上点的坐标特征,以及字母的值求代数式的值,根据反比例函数图象上点的坐标特征得出:,,进而可求出的值.
【详解】解:把点与点代入反比例函数
得:,,
∴,
故答案为:0.
10.
【分析】本题主要考查反比例函数中比例系数的几何意义,熟练掌握比例系数的几何意义是解题的关键.连接,根据三角形面积公式得到,根据比例系数的几何意义计算即可.
【详解】解:连接,
轴,
,
,
∴,
∵反比例函数图象在第二、四象限,
∴.
故答案为:.
11.
【分析】本题考查了反比例函数的应用,设出反比例函数解析式,把代入即可求解.
【详解】解:设,
度近视眼镜镜片的焦距为,
,
.
故答案为:.
12.
【分析】本题考查等腰三角形性质及判定,待定系数法求反比例函数解析式,解一元二次方程.根据题意先设点,在求出反比例函数解析式,利用等腰三角形性质列式即可得到本题答案.
【详解】解:设点,
∵点,
∴将点代入中得:,
∵,
∴为等腰直角三角形,
∴,
∵,令直线与轴交于点,
,
∴,
∵点和点关于直线对称,
∴,,
∴,即,
∴轴,
∴,
∵,
∴,整理得:,解得:或(舍),
故答案为:.
13.
【分析】作交的延长线于H,先根据反比例函数解析式求出A的坐标,设菱形的边长为a,易证,即,则点,求出a的值,写出点B的坐标,再求出,最后根据菱形的面积公式计算即可.
本题主要考查了反比例函数与几何的综合,掌握反比例函数的性质和菱形的性质是解答本题的关键.
【详解】解:(1)作交的延长线于H,
∵反比例函数的图像经过A,B两点,A点的横坐标为1,
∴,
设菱形的边长为a,
∵,
∴,
∴,
∴,
∴,
∴,(舍去),
∴点B的坐标是,,
∴菱形的面积.
故答案为:,.
14.5或或
【分析】本题考查了等腰三角形的性质,反比例函数图象上点的坐标特征,因为等腰三角形的腰不确定,所以分三种情况分别计算即可.
【详解】解:当时,;
当时,;
当时,设,
∵,
∴,
解得:,
∴或,
∴或;
综上所述,的长为5或或.
故答案为:5或或.
15.320
【分析】本题考查了反比例函数的应用,以及分式方程的应用,理解利润问题是解题的关键.先求出反比例函数解析式,再根据“该小型电器每天的销售利润达到3500元”列方程求解.
【详解】解:设售价为x元,
∵销售量是售价的反比例函数,
∴,
由题意得:,
解得:,
经检验:是原方程的解,且符合题意,
故答案为:320.
16.
【分析】本题考查了菱形的性质、反比例函数图象上点的坐标特征以及勾股定理,过点作轴于点,结合菱形的性质以及三角形的面积公式找出点的坐标,再利用反比例函数图象上点的坐标特征求出反比例函数的解析式是解题的关键.
【详解】过点作轴于点,如图所示,
∵点的坐标为,
∴,
∵四边形为菱形,且,
∴,,
∴,
在中,,,
∴,
∴,
∴,
∴,
∵点在双曲线上,
∴,解得:,
∴双曲线的解析式为,故不正确;
∵点在双曲线上,且的纵坐标为,
∴,故正确;
∵四边形为菱形,
∴,
∴,,故正确;
在中,,,
∴,
∵,
∴,,故正确,
综上可知:正确,
故答案为:.
17.(1);
(2).
【分析】()用待定系数法求反比例函数的解析式;
()根据反比例函数的增减性即可;
此题考查了反比例函数的图象及性质,熟练掌握待定系数法求反比例函数的解析式是解题的关键.
【详解】(1)∵反比例函数图象经过,
∴;
(2)由()得:,反比例函数图象位于第一、三象限,在每一象限内,随的增大而减小,
∴反比例函数图象上两点,,,
∴.
18.(1)
(2)当木板面积为时,木板对地面的压强是
【分析】此题主要考查反比例函数在实际生活中的应用,解题的关键是从实际问题中整理出函数模型,用反比例函数的知识解决实际问题,认真观察图象得出结果.
(1)设反比例函数关系式为,将点代入即可得出解析式;
(2)将代入解析式,可求出P的值.
【详解】(1)解:设,将点代入,
可得,
解得:,
与之间的函数表达式为:;
(2)解:当时, ,
故当木板面积为时,木板对地面的压强是.
19.(1)y,
(2)或
(3)
【分析】(1)先求出点A的坐标,再根据点A的坐标在反比例函数图象上求出反比例函数的表达式,设点,代入反比例函数表达式中,即可求出点B,
(2)结合图象即可得出一次函数的函数值大于反比例函数的函数值时的解集;
(3)设点,则,即可得出,则,再利用二次函数的性质即可求解.
【详解】(1)解:在一次函数的图象上,
,
即,
又在反比例函数图象上,
,即,
反比例函数的表达式为:,
一次函数的图象与反比例函数(为常数且)的图象交于,两点,
设点,
,
,
,
或,
;
(2)解:,即求一次函数的函数值大于反比例函数的函数值时的解集,
由图象可知:当或时,;
(3)解:由题意可知:设点,
,
,
,
当,即时,
的面积的最大值为:,
故答案为:.
【点睛】本题是考查反比例函数的综合题,一次函数的应用,二次函数的性质,解题的关键是熟练掌握待定系数法求函数解析式.
20.(1)图见解析,;
(2)当时,;
(3)或.
【分析】(1)根据反比例函数的图像关于原点对称即可画出另一支,将点代入中,得到反比例函数解析式,再代入,即可求得m的值;
(2)直接根据反比例函数的增减性即可求解;
(3)画出一次函数的图象,根据图象即可解答.
【详解】(1)解:如图;
将代入中,得,将代入中,得;
(2)解:当时,,当时,,
∴当时,;
(3)解:的图象与直线交于点,,作图如下:
由图可得:当时自变量的取值范围:或.
【点睛】本题考查了反比例函数的性质以及反比例函数与一次函数的交点问题,利用数形结合的思想是解题的关键.
21.(1)详见解析
(2)点C的坐标为
【分析】本题考查的是反比例函数综合题,全等三角形的判定和性质,反比例函数图像上点的坐标特征,熟练掌握反比例函数的图像和性质是解题的关键.
(1)根据直角三角形的性质得出,即可证明结论;
(2)设,得到点,代入函数解析式即可得到答案.
【详解】(1)证明:,
,
轴,
,
,
在与中,
,
;
(2)解:,
,,
设,
,
点C在反比例函数的图象上,
,解得,(舍去),
点C的坐标为.
22.(1)
(2)恒温系统在一天内保持大棚里温度不低于的时间有13.8小时.
【分析】本题考查了反比例函数和一次函数的性质和应用,解答此题时要先利用待定系数法确定函数的解析式,再观察图象特点,结合反比例函数和一次函数的性质作答.
(1)直接将点的坐标代入即可;
(2)观察图象可知:三段函数都有的点,而且段是恒温阶段,,所以计算和两段当时对应的值,相减就是结论.
【详解】(1)把代入中得:
;
(2)如图,
设的解析式为:.
把、代入中得:
,
解得:,
的解析式为:,
当时,,.
,
解得:,
.
答:恒温系统在一天内保持大棚里温度不低于的时间有13.8小时.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年人教版数学九年级下册第二十六章反比例函数综合自检卷
一、单选题
1.已知反比例函数的图象具有下列特征:在每个象限内,的值随的增大而增大,那么的取值范围是( )
A. B. C. D.
2.已知反比例函数图像经过点,下列说法中不正确的是( )
A.该函数图象在第二、四象限 B.点在该函数图象上
C.随的增大而增大 D.当时,
3.已知:平面直角坐标系中,点的坐标为,点关于原点对称的点恰好落在反比例函数的图象上,则( )
A.6 B. C.4 D.9
4.若点,,都在反比例函数的图象上,则( )
A. B.
C. D.
5.下列函数中,当时,y随x的增大而减小的是( )
A. B. C. D.
6.已知一次函数和反比例函数的图象如图所示,则二次函数的图象大致可能是( )
A. B. C. D.
7.如图所示,在x轴的正半轴上依次截取,过,分别作x轴的垂线与反比例函数的图像交于点,并设面积分别为,按此作法进行下去,(n为正整数)的值为( )
A. B. C. D.
二、填空题
8.已知反比例函数,若当时随的增大而增大,写出一个符合条件的的整数值: .
9.已知点与点均在反比例函数的图象上,则的值是 .
10.如图,反比例函数的图象上有一点P,轴于点A,点B在y轴上,,则k的值为 .
11.近视眼镜的度数度与镜片焦距成反比例,已知度的近视眼镜镜片的焦距是,则与之间的函数解析式为 .
12.如图,反比例函数的图象经过点,过点作轴,垂足为,在轴的正半轴上取一点,过点作直线的垂线,以直线为对称轴,点经轴对称变换得到的点在此反比例函数的图象上,则点的坐标是 .
13.如图,菱形的边与x轴平行,A点的横坐标为1,,反比例函数的图象经过A,B两点.
(1)点B的横坐标为 ;
(2)菱形的面积是 .
14.已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为 .
15.调查显示,某商场一款小型电器的销售量是售价的反比例函数,(调查获得的部分数据如下表).
售价x(元/台) 200 250 400 500
销售量y(台) 40 32 20 16
已知该小型电器的进价为180元/台,要使该小型电器每天的销售利润达到3500元,其售价应定为 元.
16.已知:如图,菱形在直角坐标系中,点的坐标为,对角线、相交于点,双曲线经过点,交的延长线于点,且,有下列四个结论,其中正确的结论是 .
双曲线的解析式为;;点的坐标是;.
三、解答题
17.已知反比例函数图象经过.
(1)求的值;
(2)若点,是反比例函数图象上两点,试比较,大小.
18.某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示.
(1)写出压强关于木板面积的函数解析式;
(2)当木板面积为时,木板对地面的压强是多少?
19.如图,一次函数的图象与反比例函数(为常数且)的图象交于,两点,与轴交于点.
(1)求反比例函数的表达式与点坐标;
(2)请直接写出不等式的解集;
(3)若点是线段上的一个动点,作轴交反比例函数的图象于点,则的面积的最大值为______.
20.已知反比例函数的图象的一支如图所示,它与直线交于点,.
(1)在图中,补画该反比例函数图象的另一支,并求的值;
(2)当时,求函数值的取值范围;
(3)观察图象,直接写出当时,自变量的取值范围.
21.如图:等腰直角放置在直角坐标系中,,,点A在x轴上,点B的坐标是,点C在第一象限内,作轴.
(1)求证:;
(2)若点C恰好在曲线上,求点C的坐标
22.某蔬菜生产基地用装有恒温系统的大棚栽培一种新品.如图,这是某天恒温系统从开始到关闭及关闭后,大棚里的温度随时间变化的函数图象,其中段是恒温阶段,段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求的值.
(2)求恒温系统在这一天内保持大棚内温度不低于的时间有多长.
参考答案:
1.C
【分析】本题主要考查了反比例函数图象的性质,解题的关键是熟练掌握反比例函数的性质:当时,图象在一、三象限,在每一象限内,y随x的增大而减小;当时,图象在二、四象限,在每一象限内,y随x的增大而增大.
【详解】解:∵反比例函数在每个象限内,的值随的增大而增大,
∴,
∴,
故选:C.
2.C
【分析】本题主要考查了反比例函数的图像和性质,确定反比例函数解析式中的k是解题的关键.
先确定反比例函数解析式,再根据反比例函数的性质逐项分析即可解答.
【详解】解:把点代入反比例函数可得,,即.
A、该函数的图像在第二、四象限,故A选项正确,不符合题意;
B、将点代入解析式,满足解析式,故B选项正确,不符合题意;
C、在每个象限内,y随着x的增大而增大,故C选项错误,符合题意;
D、当时,,故D选项正确,不符合题意.
故选C.
3.B
【分析】本题主要考查原点对称的点的坐标特征,反比例函数上点的坐标特征,把代入解析式即可,熟练掌握待定系数法是解题的关键.
【详解】与点关于原点对称,点的坐标为
点恰好落在反比例函数的图象上
故选:B.
4.B
【分析】本题主要考查反比例函数的图像和性质,熟练掌握反比例函数的图像和性质是解题的关键.根据解析式求出函数值比较大小即可.
【详解】解:,,都在反比例函数的图象上,
,
,
,
故,
故选B.
5.D
【分析】此题主要考查了反比例函数的性质、二次函数的性质,正确掌握相关函数增减性是解题关键.直接利用反比例函数的性质、二次函数的性质分别判断得出答案.
【详解】解:A、,当时,y随x的增大而增大,不合题意;
B、,开口方向向下,对称轴为直线,所以当时,y随x的增大而增大,当时,y随x的增大而减小,不合题意;
C、,开口方向向下,对称轴为直线,当时,y随x的增大而增大,当时,y随x的增大而减小,不合题意;
D、,当时,y随x的增大而减小,符合题意;
故选:D.
6.B
【分析】本题考查了一次函数的图象、反比例函数的图象以及二次函数的图象,解题的关键是根据一次函数与反比例函数的图象找出、、的正负.根据一次函数与反比例函数图象找出、、的正负,再根据抛物线的对称轴为,得出二次函数对称轴在轴右侧,比对四个选项的函数图象即可得出结论.
【详解】解:∵一次函数图象过第一、二、四象限,
∴,
∴,
∴二次函数开口向下,对称轴在轴右侧;
∵反比例函数的图象在第一、三象限,
∴,
∴与轴交点在轴上方,
满足上述条件的函数图象只有选项B.
故选:B.
7.D
【分析】主要考查了反比例函数中k的几何意义,根据反比例函数中k的几何意义再结合图象即可解答.
【详解】解:因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,.
又因为,
所以,,,,,
,
依此类推:的值为.
故选:D.
8.(答案不唯一)
【分析】本题考查反比例函数的图像与性质,涉及反比例函数图像增减性与常数符号的关系,熟记当时随的增大而增大,则即可得到答案,熟记反比例函数图像增减性与常数符号的关系是解决问题的关键.
【详解】解:反比例函数,当时随的增大而增大,
,
一个符合条件的的整数值可取(写出任意负整数即可),
故答案为:(答案不唯一).
9.0
【分析】本题主要考查了反比例函数图象上点的坐标特征,以及字母的值求代数式的值,根据反比例函数图象上点的坐标特征得出:,,进而可求出的值.
【详解】解:把点与点代入反比例函数
得:,,
∴,
故答案为:0.
10.
【分析】本题主要考查反比例函数中比例系数的几何意义,熟练掌握比例系数的几何意义是解题的关键.连接,根据三角形面积公式得到,根据比例系数的几何意义计算即可.
【详解】解:连接,
轴,
,
,
∴,
∵反比例函数图象在第二、四象限,
∴.
故答案为:.
11.
【分析】本题考查了反比例函数的应用,设出反比例函数解析式,把代入即可求解.
【详解】解:设,
度近视眼镜镜片的焦距为,
,
.
故答案为:.
12.
【分析】本题考查等腰三角形性质及判定,待定系数法求反比例函数解析式,解一元二次方程.根据题意先设点,在求出反比例函数解析式,利用等腰三角形性质列式即可得到本题答案.
【详解】解:设点,
∵点,
∴将点代入中得:,
∵,
∴为等腰直角三角形,
∴,
∵,令直线与轴交于点,
,
∴,
∵点和点关于直线对称,
∴,,
∴,即,
∴轴,
∴,
∵,
∴,整理得:,解得:或(舍),
故答案为:.
13.
【分析】作交的延长线于H,先根据反比例函数解析式求出A的坐标,设菱形的边长为a,易证,即,则点,求出a的值,写出点B的坐标,再求出,最后根据菱形的面积公式计算即可.
本题主要考查了反比例函数与几何的综合,掌握反比例函数的性质和菱形的性质是解答本题的关键.
【详解】解:(1)作交的延长线于H,
∵反比例函数的图像经过A,B两点,A点的横坐标为1,
∴,
设菱形的边长为a,
∵,
∴,
∴,
∴,
∴,
∴,(舍去),
∴点B的坐标是,,
∴菱形的面积.
故答案为:,.
14.5或或
【分析】本题考查了等腰三角形的性质,反比例函数图象上点的坐标特征,因为等腰三角形的腰不确定,所以分三种情况分别计算即可.
【详解】解:当时,;
当时,;
当时,设,
∵,
∴,
解得:,
∴或,
∴或;
综上所述,的长为5或或.
故答案为:5或或.
15.320
【分析】本题考查了反比例函数的应用,以及分式方程的应用,理解利润问题是解题的关键.先求出反比例函数解析式,再根据“该小型电器每天的销售利润达到3500元”列方程求解.
【详解】解:设售价为x元,
∵销售量是售价的反比例函数,
∴,
由题意得:,
解得:,
经检验:是原方程的解,且符合题意,
故答案为:320.
16.
【分析】本题考查了菱形的性质、反比例函数图象上点的坐标特征以及勾股定理,过点作轴于点,结合菱形的性质以及三角形的面积公式找出点的坐标,再利用反比例函数图象上点的坐标特征求出反比例函数的解析式是解题的关键.
【详解】过点作轴于点,如图所示,
∵点的坐标为,
∴,
∵四边形为菱形,且,
∴,,
∴,
在中,,,
∴,
∴,
∴,
∴,
∵点在双曲线上,
∴,解得:,
∴双曲线的解析式为,故不正确;
∵点在双曲线上,且的纵坐标为,
∴,故正确;
∵四边形为菱形,
∴,
∴,,故正确;
在中,,,
∴,
∵,
∴,,故正确,
综上可知:正确,
故答案为:.
17.(1);
(2).
【分析】()用待定系数法求反比例函数的解析式;
()根据反比例函数的增减性即可;
此题考查了反比例函数的图象及性质,熟练掌握待定系数法求反比例函数的解析式是解题的关键.
【详解】(1)∵反比例函数图象经过,
∴;
(2)由()得:,反比例函数图象位于第一、三象限,在每一象限内,随的增大而减小,
∴反比例函数图象上两点,,,
∴.
18.(1)
(2)当木板面积为时,木板对地面的压强是
【分析】此题主要考查反比例函数在实际生活中的应用,解题的关键是从实际问题中整理出函数模型,用反比例函数的知识解决实际问题,认真观察图象得出结果.
(1)设反比例函数关系式为,将点代入即可得出解析式;
(2)将代入解析式,可求出P的值.
【详解】(1)解:设,将点代入,
可得,
解得:,
与之间的函数表达式为:;
(2)解:当时, ,
故当木板面积为时,木板对地面的压强是.
19.(1)y,
(2)或
(3)
【分析】(1)先求出点A的坐标,再根据点A的坐标在反比例函数图象上求出反比例函数的表达式,设点,代入反比例函数表达式中,即可求出点B,
(2)结合图象即可得出一次函数的函数值大于反比例函数的函数值时的解集;
(3)设点,则,即可得出,则,再利用二次函数的性质即可求解.
【详解】(1)解:在一次函数的图象上,
,
即,
又在反比例函数图象上,
,即,
反比例函数的表达式为:,
一次函数的图象与反比例函数(为常数且)的图象交于,两点,
设点,
,
,
,
或,
;
(2)解:,即求一次函数的函数值大于反比例函数的函数值时的解集,
由图象可知:当或时,;
(3)解:由题意可知:设点,
,
,
,
当,即时,
的面积的最大值为:,
故答案为:.
【点睛】本题是考查反比例函数的综合题,一次函数的应用,二次函数的性质,解题的关键是熟练掌握待定系数法求函数解析式.
20.(1)图见解析,;
(2)当时,;
(3)或.
【分析】(1)根据反比例函数的图像关于原点对称即可画出另一支,将点代入中,得到反比例函数解析式,再代入,即可求得m的值;
(2)直接根据反比例函数的增减性即可求解;
(3)画出一次函数的图象,根据图象即可解答.
【详解】(1)解:如图;
将代入中,得,将代入中,得;
(2)解:当时,,当时,,
∴当时,;
(3)解:的图象与直线交于点,,作图如下:
由图可得:当时自变量的取值范围:或.
【点睛】本题考查了反比例函数的性质以及反比例函数与一次函数的交点问题,利用数形结合的思想是解题的关键.
21.(1)详见解析
(2)点C的坐标为
【分析】本题考查的是反比例函数综合题,全等三角形的判定和性质,反比例函数图像上点的坐标特征,熟练掌握反比例函数的图像和性质是解题的关键.
(1)根据直角三角形的性质得出,即可证明结论;
(2)设,得到点,代入函数解析式即可得到答案.
【详解】(1)证明:,
,
轴,
,
,
在与中,
,
;
(2)解:,
,,
设,
,
点C在反比例函数的图象上,
,解得,(舍去),
点C的坐标为.
22.(1)
(2)恒温系统在一天内保持大棚里温度不低于的时间有13.8小时.
【分析】本题考查了反比例函数和一次函数的性质和应用,解答此题时要先利用待定系数法确定函数的解析式,再观察图象特点,结合反比例函数和一次函数的性质作答.
(1)直接将点的坐标代入即可;
(2)观察图象可知:三段函数都有的点,而且段是恒温阶段,,所以计算和两段当时对应的值,相减就是结论.
【详解】(1)把代入中得:
;
(2)如图,
设的解析式为:.
把、代入中得:
,
解得:,
的解析式为:,
当时,,.
,
解得:,
.
答:恒温系统在一天内保持大棚里温度不低于的时间有13.8小时.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
