第十八章 平行四边形综合自检卷(含解析)
文档属性
| 名称 | 第十八章 平行四边形综合自检卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 10:22:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年人教版数学八年级下册第十八章平行四边形综合自检卷
一、单选题
1.在中,如果 .那么等于 ( )
A. B. C. D.
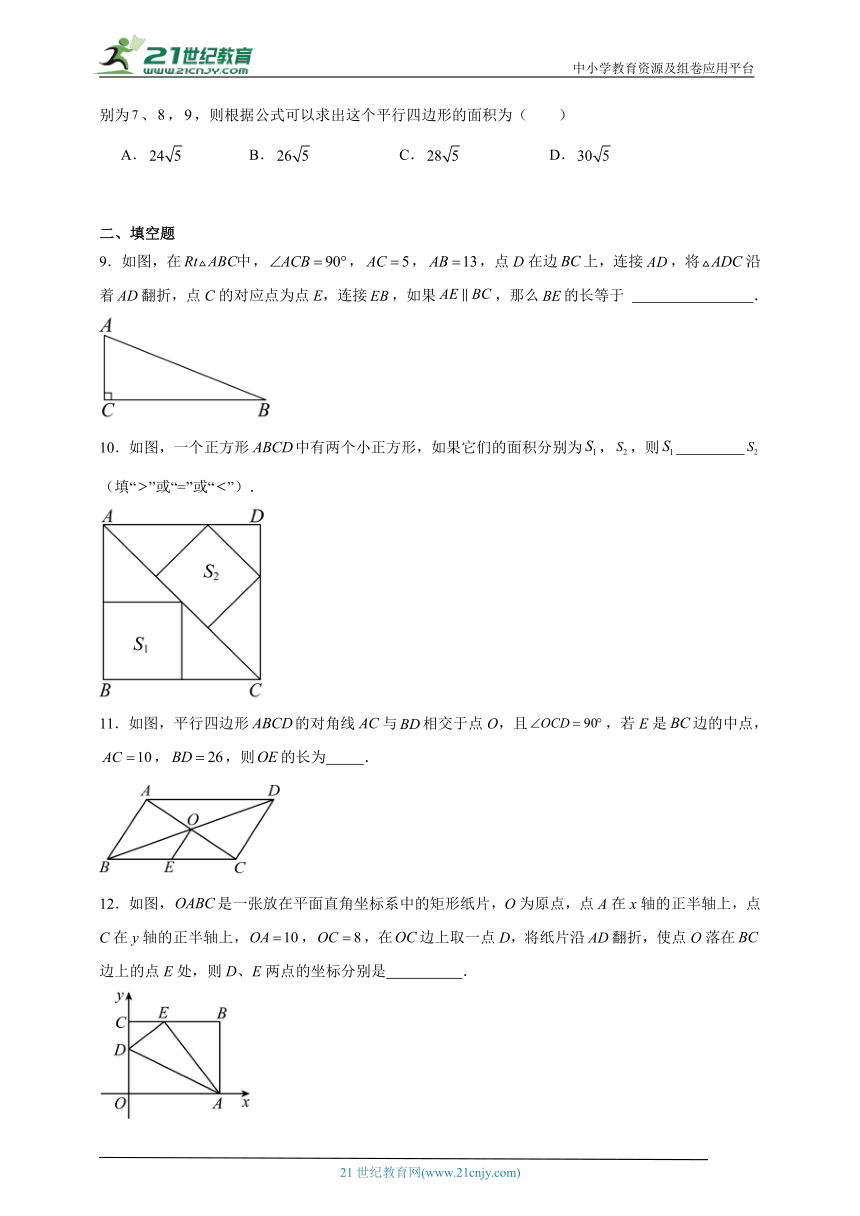
2.如图,在中,,点M是斜边的中点,以为边作正方形,,则( )
A. B. C.12 D.16
3.如图,菱形中,,,,,垂足分别为E、F.则的周长是( )
A. B. C. D.
4.如图,矩形的对角线,相交于点.若,则的值为( )
A. B. C. D.
5.如图,在中,,于点,和的角平分线相交于点为边的中点,,则( )
A. B. C. D.
6.如图,已知长方形纸片,M为边上的一点,将纸片沿,折叠使点A落在处,点D落在处,如果,那么的度数为( )
A. B. C. D.
7.汉代数学家赵爽为了证明勾股定理,创制了一幅“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形、正方形、正方形 的面积分别为. 若 ,则 的值是 ( )
A.567 B.666 C.777 D.675
8.南宋杰出数学家秦九韶(出生于安岳县龙台镇),今年是他诞辰周年及其巨著《数书九章》成书周年,他的“三斜求积”术与西方数学家海伦公式如出一辙:
,其中.(海伦)
,其中.(秦九韶)
(表示三角形的面积,、、分别为三角形三边长)在世界数学史上,人们为了纪念这两位伟大的数学家,特将这两个公式命名为“秦九韶﹣海伦”公式.已知平行四边形的两邻边和一条对角线分别为、,,则根据公式可以求出这个平行四边形的面积为( )
A. B. C. D.
二、填空题
9.如图,在,,,,点D在边上,连接,将沿着翻折,点C的对应点为点E,连接,如果,那么的长等于 .
10.如图,一个正方形中有两个小正方形,如果它们的面积分别为,,则 (填“”或“=”或“”).
11.如图,平行四边形的对角线与相交于点O,且,若E是边的中点,,,则的长为 .
12.如图,是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,,,在边上取一点D,将纸片沿翻折,使点O落在边上的点E处,则D、E两点的坐标分别是 .
13.如图,矩形纸片的对角线,相交于点,,将矩形纸片翻折,使点恰好落在点处,折痕为,点在边上,则的长为 .
14.如图,面积为的正方形的边在数轴上,点表示的数为1.将正方形沿着数轴水平移动,移动后的正方形记为,点的对应点分别为,移动后的正方形与原正方形重叠部分图形的面积记为.当时,数轴上点表示的数是 (可用含的代数式表示).
15.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的边长为5,小正方形的面积为4,若x,y表示直角三角形的两直角边长,给出下列四个结论:①;②;③;④;⑤,.其中正确的结论有 .
16.如图,D,E,F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF的周长为 .
三、解答题
17.已知:如图,在中,,点是边中点,延长至点,使得,连接,当时,求的度数.
18.如图,在中,为线段上一点,连接,将线段绕点A逆时针旋转得到线段,作射线.
(1)求证:,并求的度数;
(2)若F为中点,连接,连接并延长,交射线于点G,当时.
①求的长;
②直接写出的长.
19.如图,点E为平行四边形的边上的一点,连接并延长使,连接并延长,使,点H是的中点,连接,.
(1)若,,求的度数;
(2)求证:四边形为平行四边形;
(3)连接,交于点O,若,,直接写出的长度.
20.如图,矩形中,,,点E、点F分别是对角线上的点,且,过点E作,交于点G,平移,使B、F的对应点分别是G、H,连接.
(1)当是以为腰长的等腰三角形时,求的长;
(2)连接.判断四边形的形状,并说明理由;
21.如图,在中,为对角线,垂直平分分别交、于点E、F,交于点O.
(1)试说明:;
(2)试说明:;
(3)如果在中,,,有两动点P、Q分别从B、D两点同时出发,沿和各边运动一周,即点P自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形是平行四边形时,求m与n满足的数量关系.(画出示意图)
22.如图1,在中,于,且.
(1)求证:是等腰三角形;
(2)已知,动点从点出发以的速度沿线段向点运动,同时动点从点出发以相同的速度沿线段向点运动,当其中一点到达终点时整个运动都停止.设运动时间为.若的边与平行,求的值;
(3)在(2)的条件下,设的垂直平分线交于点,利用图3及备用图分析:在点运动的过程中,能否成为等腰三角形?若能,求出的值;若不能,请说明理由.
参考答案:
1.D
【分析】本题考查平行四边形的性质,解题的关键是根据平行四边形的性质,则,是对角,则;再根据,即可求出.
【详解】∵四边形是平行四边形,
∴,
∵,
∴,
∴,
故选:D.
2.B
【分析】本题考查了直角三角形斜边上的中线等于斜边的一半,正方形的面积计算公式,直角三角形面积的计算公式,勾股定理,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.
先根据正方形的面积求出的长,然后根据直角三角形斜边上的中线等于斜边的一半求出的长,最后根据勾股定理求出的长,然后即可求出直角三角形的面积.
【详解】∵四边形是正方形,
又∵,
在中,点是斜边的中点,
即,
在中,,
,
,
故选:B.
3.C
【分析】本题考查了菱形的性质、勾股定理、含30度角的直角三角形的性质、等边三角形的判定与性质,熟练掌握菱形的性质是解题关键.先求出,,再判断出是等边三角形,根据等边三角形的性质求解即可得.
【详解】解:∵菱形中,,,,
,,
,
,
同理可得:,
,,
是等边三角形,
则的周长是,
故选:C.
4.C
【分析】本题考查了矩形的性质,等边三角形的判定和性质,直角三角形的性质,先证是等边三角形,可得,由直角三角形的性质可求解.
【详解】四边形是矩形,
,
,
∴是等边三角形,
,
,
,
,
故选:C.
5.C
【分析】本题考查了直角三角形的性质、等边三角形的判定与性质、角平分线的定义、三角形内角和定理,连接,根据直角三角形斜边上的中线等于斜边的一半得出是等边三角形,进而得出,由角平分线的定义结合三角形内角和定理,即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,连接,
,为边的中点,
,
又,
,
是等边三角形,
,
,
,
和的角平分线相交于点,
,
,
,
故选:C.
6.D
【分析】本题主要考查了轴对称的性质,矩形的性质,熟练掌握折叠的性质是解题的关键.利用折叠的性质得到对应角相等,然后利用平角定理求出角的度数.
【详解】解:将纸片沿,折叠使点A落在处,点D落在处,
,,
,
,
,
, ,
,
.
故选D.
7.D
【分析】本题考查正方形的知识,解题的关键是掌握正方形的性质,直角三角形的性质,全等三角形的性质.设直角三角形的面积为,正方形的面积为;由题意得,正方形的面积为:;正方形的面积为:;最后根据,即可.
【详解】设直角三角形的面积为,正方形的面积为,
∴正方形的面积为:;正方形的面积为:,
∵,
∴,
∴,
解得:,
∴.
故选:D.
8.A
【分析】平行四边形其中一条对角线可将平行四边形的面积平均分成两部分,根据题意给出的公式可求出其中一个三角形的面积即可得出答案.
【详解】解:平行四边形的两邻边和一条对角线可构造成一个三角形,
该三角形的边长为、,,
∴由题意给出的公式可知:,
∴该三角形的面积为:,
∴该平行四边形的面积为:,
故选:A.
【点睛】本题考查了平行四边形的性质,二次根式的性质和化简,学生的阅读能力,解题的关键是正确理解题目给出的公式以及平行四边形的性质,本题属于中等题型.
9.
【分析】由,,,根据勾股定理求得,由翻折得,由,得,,可证明四边形是正方形,则,所以,则,于是得到问题的答案.
【详解】解:∵,,,
∴,
由翻折得,
∵,
∴,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,
∴,
∴,
故答案为:.
【点睛】此题重点考查勾股定理、轴对称的性质、平行线的性质、正方形的判定与性质等知识,求得是解题的关键.
10.
【分析】本题考查了正方形的性质,勾股定理等等知识,设正方形的边长为6,然后求出与的值,问题得解.
【详解】解:如图,设正方形的边长为6,
∵是正方形的对角线,
,,
∴,
又∵四边形与四边形是正方形,
,,
,,
,,
∴.
故答案为:.
11.6
【分析】本题主要考查了平行四边形的性质,三角形中位线定理,勾股定理,证明为的中位线是解题的关键.先利用勾股定理求出,再证明为的中位线,则.
【详解】解:∵,
∴,
∵四边形是平行四边形,,,
∴,
∴,
又∵点E为边的中点,
∴为的中位线,
∴,
故答案为:6.
12.
【分析】先由矩形的性质得到,再根据折叠的性质得,在中,利用勾股定理可计算出,则,即可得到点E的坐标,设,则,在中根据勾股定理有,解方程求出x,即可确定D点坐标.
【详解】解:∵四边形为矩形,
∴,
∵将纸片沿翻折,使点O落在边上的点E处,
∴,
在中,,
∴,
∴,
∴点E的坐标是,
设,则,
在中,
∵,
∴,
∴,
∴D点坐标为.
故答案为:.
【点睛】本题考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了点的坐标、矩形的性质以及勾股定理.
13.
【分析】本题考查翻折变换,等边三角形的判定和性质,含30度的直角三角形的性质;首先证明是等边三角形,根据含30度角的直角三角形的性质得出,证明,根据,即可求解.
【详解】解:四边形是矩形,
,,
由翻折性质可知:,,
,
是等边三角形,
,
,,则
,,
,
故答案为:6.
14.或
【分析】本题考查了实数与数轴,数轴上两点间的距离,分情况讨论,利用得到是解题的关键.根据正方形的面积得到正方形的边长,分情况讨论:当正方形沿着数轴水平向右移动时,当时得到,求出,根据点表示的数为,可得到点表示的数;正方形沿着数轴水平向左移动时, 当时得到,根据点表示的数为,可得到点表示的数.
【详解】解:如图,当正方形沿着数轴水平向右移动时,
正方形的面积为,
正方形的边长为,
移动后的正方形与原正方形重叠部分图形的面积记为,
当时,,
,
,
点表示的数为,
点表示的数为.
当正方形沿着数轴水平向左移动时,
移动后的正方形与原正方形重叠部分图形的面积记为,
当时,,
,
,
点表示的数为,
点表示的数为.
综上所述:点表示的数为或.
故答案为:或.
15.
【分析】本题考查勾股定理及正方形和三角形的边的关系,此图被称为“弦图”,根据正方形的性质、直角三角形的性质、直角三角形面积的计算公式及勾股定理解答,熟悉勾股定理并认清图中的关系是解题的关键.
【详解】解:给图形标注字母如下:
为直角三角形,
∴根据勾股定理:,故选项①正确;
②由图可知,故选项②正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为 即故选项③正确;
④由
又
∴(1)+(2)得,
整理得,
故选项④错误,
⑤由④可知,故选项⑤错误,
∴正确结论有,
故答案为:.
16.5
【解析】略
17.
【分析】本题考查了直角三角形斜边上的中线性质、勾股定理的逆定理以及等边三角形的判定和性质,熟练掌握直角三角形斜边上的中线性质和勾股定理的逆定理是解题的关键.由直角三角形斜边上的中线性质得,则,再由勾股定理的逆定理得是直角三角形,且,即可得出结论.
【详解】解:,点是边中点,
,
,
,
,
是直角三角形,且,
取的中点F,连接,
,
∴,
,即的度数为
18.(1)证明见详解;
(2)①;②
【分析】本题是几何变换综合题,主要考查了等腰直角三角形的性质,全等三角形的判定与性质,勾股定理,直角三角形斜边上中线的性质等知识,熟练掌握直角三角形斜边上中线的性质是解题的关键.
(1)利用证明,得,即可解决问题;
(2)①利用勾股定理求出的长,再利用直角三角形斜边上中线的性质可得答案;
②利用等角对等边说明点为的中点,再利用直角三角形斜边上中线的性质可得答案.
【详解】(1)证明:∵,
又
;
(2)①在中,∵
又∵为中点,,
则.
②在中,为的中点,
19.(1)
(2)见解析
(3)2
【分析】本题考查了平行四边形的判定与性质、三角形中位线定理、平行线的性质.
(1)由平行四边形的性质和平行线的判定和性质得出答案即可;
(2)由平行四边形的性质得,,再证是的中位线,得,,证出,,然后由平行四边形的判定即可得出结论;
(3)连接、、,由三角形的中位线定理以及平行四边形的判定和性质解答即可.
【详解】(1)∵四边形是平行四边形,
∴,
∴,
∵在中,,
∴;
(2)∵,,
∴是的中位线,
∴,,
∵H为FG的中点,
∴,
∴,,
∵四边形是平行四边形,
∴,,
∴,,
∴四边形是平行四边形;
(3)如图,连接,,
∵,H为FG的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴.
20.(1)的长为2或5
(2)矩形,详见解析
【分析】(1)利用勾股定理求得的长,再分和情况讨论即可求解;
(2)证明,推出,,再证明四边形是平行四边形,据此即可得到四边形是矩形.
【详解】(1)解:矩形中,,,
∴,
①当时,;
②当时,,
在中,,,
∴,
∴,
∴.
综上所述,CE的长为2或5;
(2)证明:∵四边形是矩形,
∴,,
∴,
在和中,
∴;
∴,,
∴,即,
∴,
∵平移得,
∴,,
∴,,
∴四边形是平行四边形,
∵,
∴,
∴,
∴四边形是矩形.
【点睛】本题考查了矩形的判定和性质,全等三角形的判定和性质,勾股定理,等腰三角形的性质等知识点.解题的关键是灵活运用所学知识解决问题.
21.(1)见解析
(2)见解析
(3)
【分析】(1)根据证即可;
(2)推出,根据平行四边形性质求出,推出,根据证即可;
(3)求出的周长,分为三种情况,①当P在上,Q在上,②当P在上,Q在上,③当P在上,Q在上,每种情况都等于的周长.
【详解】(1)解:四边形是平行四边形,
,
,
垂直平分,
,
在和中,
,
(),
;
(2)解:四边形是平行四边形,
,,
,
,
在和中,
,
();
(3)解:垂直平分,
,
,
,
,
的周长是
,
故的周长也是,
①当P在上,Q在上,
,
,
在和中
,
(),
,
②当P在上,Q在上,
,
,
,
,
在和中
,
(),
,
,
,
;
③当P在上,Q在上,
,
,
,
,
四边形是平行四边形,
,
,
,
在和中
,
(),
,
;
综上所述:m与n满足的数量关系是.
【点睛】本题考查了平行四边形的性质和判定,全等三角形的性质和判定,平行线的性质和判定的综合运用,掌握性质及判定方法,能根据和的不同位置进行分类讨论是解题的关键.
22.(1)见解析
(2)2.5或3
(3)能,t值为4.5或5或
【分析】(1)设,,,则,由勾股定理求出,即可得出结论;
(2)由的面积求出、、、的长;①当时,;②当时,;得出方程,解方程即可;
(3)由勾股定理可得,根据题意得出当点在上,即时,为等腰三角形,有3种可能:①;②;③;分别得出方程,解方程即可.
【详解】(1)证明:设,,,则,
,
,
,
,
是等腰三角形;
(2)解:,而,
,
则,,,,
由题意得:
若的边与平行,存在以下两种情况:
①当时,如图2,,,
,
,
,
,
,
;
②当时,如图3,同理得:,
,
,
若的边与平行时,值为2.5或3;
(3)解:能成为等腰三角形;
是的垂直平分线,,
,,
,
∴,
,
是的中位线,
,
由勾股定理得:,
①当时,是等腰三角形,
,
;
②当时,如图5,是等腰三角形,此时与重合,
;
③当时,是等腰三角形,
如图6,过点作于,交于,连接,
,
设,则,
在中,由勾股定理得:,
,
,
,
由勾股定理得:,
设,,
,
,
,
,
在中,,
,
,
,
,
综上,的值是或5或.
【点睛】本题是三角形的综合题,考查了勾股定理,等腰三角形的判定与性质,三角形的面积,完全平方公式,线段垂直平分线的性质,三角形的中位线定理,解方程等知识,本题有一定难度,需要进行分类讨论才能得出结果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年人教版数学八年级下册第十八章平行四边形综合自检卷
一、单选题
1.在中,如果 .那么等于 ( )
A. B. C. D.
2.如图,在中,,点M是斜边的中点,以为边作正方形,,则( )
A. B. C.12 D.16
3.如图,菱形中,,,,,垂足分别为E、F.则的周长是( )
A. B. C. D.
4.如图,矩形的对角线,相交于点.若,则的值为( )
A. B. C. D.
5.如图,在中,,于点,和的角平分线相交于点为边的中点,,则( )
A. B. C. D.
6.如图,已知长方形纸片,M为边上的一点,将纸片沿,折叠使点A落在处,点D落在处,如果,那么的度数为( )
A. B. C. D.
7.汉代数学家赵爽为了证明勾股定理,创制了一幅“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形、正方形、正方形 的面积分别为. 若 ,则 的值是 ( )
A.567 B.666 C.777 D.675
8.南宋杰出数学家秦九韶(出生于安岳县龙台镇),今年是他诞辰周年及其巨著《数书九章》成书周年,他的“三斜求积”术与西方数学家海伦公式如出一辙:
,其中.(海伦)
,其中.(秦九韶)
(表示三角形的面积,、、分别为三角形三边长)在世界数学史上,人们为了纪念这两位伟大的数学家,特将这两个公式命名为“秦九韶﹣海伦”公式.已知平行四边形的两邻边和一条对角线分别为、,,则根据公式可以求出这个平行四边形的面积为( )
A. B. C. D.
二、填空题
9.如图,在,,,,点D在边上,连接,将沿着翻折,点C的对应点为点E,连接,如果,那么的长等于 .
10.如图,一个正方形中有两个小正方形,如果它们的面积分别为,,则 (填“”或“=”或“”).
11.如图,平行四边形的对角线与相交于点O,且,若E是边的中点,,,则的长为 .
12.如图,是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,,,在边上取一点D,将纸片沿翻折,使点O落在边上的点E处,则D、E两点的坐标分别是 .
13.如图,矩形纸片的对角线,相交于点,,将矩形纸片翻折,使点恰好落在点处,折痕为,点在边上,则的长为 .
14.如图,面积为的正方形的边在数轴上,点表示的数为1.将正方形沿着数轴水平移动,移动后的正方形记为,点的对应点分别为,移动后的正方形与原正方形重叠部分图形的面积记为.当时,数轴上点表示的数是 (可用含的代数式表示).
15.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的边长为5,小正方形的面积为4,若x,y表示直角三角形的两直角边长,给出下列四个结论:①;②;③;④;⑤,.其中正确的结论有 .
16.如图,D,E,F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF的周长为 .
三、解答题
17.已知:如图,在中,,点是边中点,延长至点,使得,连接,当时,求的度数.
18.如图,在中,为线段上一点,连接,将线段绕点A逆时针旋转得到线段,作射线.
(1)求证:,并求的度数;
(2)若F为中点,连接,连接并延长,交射线于点G,当时.
①求的长;
②直接写出的长.
19.如图,点E为平行四边形的边上的一点,连接并延长使,连接并延长,使,点H是的中点,连接,.
(1)若,,求的度数;
(2)求证:四边形为平行四边形;
(3)连接,交于点O,若,,直接写出的长度.
20.如图,矩形中,,,点E、点F分别是对角线上的点,且,过点E作,交于点G,平移,使B、F的对应点分别是G、H,连接.
(1)当是以为腰长的等腰三角形时,求的长;
(2)连接.判断四边形的形状,并说明理由;
21.如图,在中,为对角线,垂直平分分别交、于点E、F,交于点O.
(1)试说明:;
(2)试说明:;
(3)如果在中,,,有两动点P、Q分别从B、D两点同时出发,沿和各边运动一周,即点P自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形是平行四边形时,求m与n满足的数量关系.(画出示意图)
22.如图1,在中,于,且.
(1)求证:是等腰三角形;
(2)已知,动点从点出发以的速度沿线段向点运动,同时动点从点出发以相同的速度沿线段向点运动,当其中一点到达终点时整个运动都停止.设运动时间为.若的边与平行,求的值;
(3)在(2)的条件下,设的垂直平分线交于点,利用图3及备用图分析:在点运动的过程中,能否成为等腰三角形?若能,求出的值;若不能,请说明理由.
参考答案:
1.D
【分析】本题考查平行四边形的性质,解题的关键是根据平行四边形的性质,则,是对角,则;再根据,即可求出.
【详解】∵四边形是平行四边形,
∴,
∵,
∴,
∴,
故选:D.
2.B
【分析】本题考查了直角三角形斜边上的中线等于斜边的一半,正方形的面积计算公式,直角三角形面积的计算公式,勾股定理,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.
先根据正方形的面积求出的长,然后根据直角三角形斜边上的中线等于斜边的一半求出的长,最后根据勾股定理求出的长,然后即可求出直角三角形的面积.
【详解】∵四边形是正方形,
又∵,
在中,点是斜边的中点,
即,
在中,,
,
,
故选:B.
3.C
【分析】本题考查了菱形的性质、勾股定理、含30度角的直角三角形的性质、等边三角形的判定与性质,熟练掌握菱形的性质是解题关键.先求出,,再判断出是等边三角形,根据等边三角形的性质求解即可得.
【详解】解:∵菱形中,,,,
,,
,
,
同理可得:,
,,
是等边三角形,
则的周长是,
故选:C.
4.C
【分析】本题考查了矩形的性质,等边三角形的判定和性质,直角三角形的性质,先证是等边三角形,可得,由直角三角形的性质可求解.
【详解】四边形是矩形,
,
,
∴是等边三角形,
,
,
,
,
故选:C.
5.C
【分析】本题考查了直角三角形的性质、等边三角形的判定与性质、角平分线的定义、三角形内角和定理,连接,根据直角三角形斜边上的中线等于斜边的一半得出是等边三角形,进而得出,由角平分线的定义结合三角形内角和定理,即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,连接,
,为边的中点,
,
又,
,
是等边三角形,
,
,
,
和的角平分线相交于点,
,
,
,
故选:C.
6.D
【分析】本题主要考查了轴对称的性质,矩形的性质,熟练掌握折叠的性质是解题的关键.利用折叠的性质得到对应角相等,然后利用平角定理求出角的度数.
【详解】解:将纸片沿,折叠使点A落在处,点D落在处,
,,
,
,
,
, ,
,
.
故选D.
7.D
【分析】本题考查正方形的知识,解题的关键是掌握正方形的性质,直角三角形的性质,全等三角形的性质.设直角三角形的面积为,正方形的面积为;由题意得,正方形的面积为:;正方形的面积为:;最后根据,即可.
【详解】设直角三角形的面积为,正方形的面积为,
∴正方形的面积为:;正方形的面积为:,
∵,
∴,
∴,
解得:,
∴.
故选:D.
8.A
【分析】平行四边形其中一条对角线可将平行四边形的面积平均分成两部分,根据题意给出的公式可求出其中一个三角形的面积即可得出答案.
【详解】解:平行四边形的两邻边和一条对角线可构造成一个三角形,
该三角形的边长为、,,
∴由题意给出的公式可知:,
∴该三角形的面积为:,
∴该平行四边形的面积为:,
故选:A.
【点睛】本题考查了平行四边形的性质,二次根式的性质和化简,学生的阅读能力,解题的关键是正确理解题目给出的公式以及平行四边形的性质,本题属于中等题型.
9.
【分析】由,,,根据勾股定理求得,由翻折得,由,得,,可证明四边形是正方形,则,所以,则,于是得到问题的答案.
【详解】解:∵,,,
∴,
由翻折得,
∵,
∴,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,
∴,
∴,
故答案为:.
【点睛】此题重点考查勾股定理、轴对称的性质、平行线的性质、正方形的判定与性质等知识,求得是解题的关键.
10.
【分析】本题考查了正方形的性质,勾股定理等等知识,设正方形的边长为6,然后求出与的值,问题得解.
【详解】解:如图,设正方形的边长为6,
∵是正方形的对角线,
,,
∴,
又∵四边形与四边形是正方形,
,,
,,
,,
∴.
故答案为:.
11.6
【分析】本题主要考查了平行四边形的性质,三角形中位线定理,勾股定理,证明为的中位线是解题的关键.先利用勾股定理求出,再证明为的中位线,则.
【详解】解:∵,
∴,
∵四边形是平行四边形,,,
∴,
∴,
又∵点E为边的中点,
∴为的中位线,
∴,
故答案为:6.
12.
【分析】先由矩形的性质得到,再根据折叠的性质得,在中,利用勾股定理可计算出,则,即可得到点E的坐标,设,则,在中根据勾股定理有,解方程求出x,即可确定D点坐标.
【详解】解:∵四边形为矩形,
∴,
∵将纸片沿翻折,使点O落在边上的点E处,
∴,
在中,,
∴,
∴,
∴点E的坐标是,
设,则,
在中,
∵,
∴,
∴,
∴D点坐标为.
故答案为:.
【点睛】本题考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了点的坐标、矩形的性质以及勾股定理.
13.
【分析】本题考查翻折变换,等边三角形的判定和性质,含30度的直角三角形的性质;首先证明是等边三角形,根据含30度角的直角三角形的性质得出,证明,根据,即可求解.
【详解】解:四边形是矩形,
,,
由翻折性质可知:,,
,
是等边三角形,
,
,,则
,,
,
故答案为:6.
14.或
【分析】本题考查了实数与数轴,数轴上两点间的距离,分情况讨论,利用得到是解题的关键.根据正方形的面积得到正方形的边长,分情况讨论:当正方形沿着数轴水平向右移动时,当时得到,求出,根据点表示的数为,可得到点表示的数;正方形沿着数轴水平向左移动时, 当时得到,根据点表示的数为,可得到点表示的数.
【详解】解:如图,当正方形沿着数轴水平向右移动时,
正方形的面积为,
正方形的边长为,
移动后的正方形与原正方形重叠部分图形的面积记为,
当时,,
,
,
点表示的数为,
点表示的数为.
当正方形沿着数轴水平向左移动时,
移动后的正方形与原正方形重叠部分图形的面积记为,
当时,,
,
,
点表示的数为,
点表示的数为.
综上所述:点表示的数为或.
故答案为:或.
15.
【分析】本题考查勾股定理及正方形和三角形的边的关系,此图被称为“弦图”,根据正方形的性质、直角三角形的性质、直角三角形面积的计算公式及勾股定理解答,熟悉勾股定理并认清图中的关系是解题的关键.
【详解】解:给图形标注字母如下:
为直角三角形,
∴根据勾股定理:,故选项①正确;
②由图可知,故选项②正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为 即故选项③正确;
④由
又
∴(1)+(2)得,
整理得,
故选项④错误,
⑤由④可知,故选项⑤错误,
∴正确结论有,
故答案为:.
16.5
【解析】略
17.
【分析】本题考查了直角三角形斜边上的中线性质、勾股定理的逆定理以及等边三角形的判定和性质,熟练掌握直角三角形斜边上的中线性质和勾股定理的逆定理是解题的关键.由直角三角形斜边上的中线性质得,则,再由勾股定理的逆定理得是直角三角形,且,即可得出结论.
【详解】解:,点是边中点,
,
,
,
,
是直角三角形,且,
取的中点F,连接,
,
∴,
,即的度数为
18.(1)证明见详解;
(2)①;②
【分析】本题是几何变换综合题,主要考查了等腰直角三角形的性质,全等三角形的判定与性质,勾股定理,直角三角形斜边上中线的性质等知识,熟练掌握直角三角形斜边上中线的性质是解题的关键.
(1)利用证明,得,即可解决问题;
(2)①利用勾股定理求出的长,再利用直角三角形斜边上中线的性质可得答案;
②利用等角对等边说明点为的中点,再利用直角三角形斜边上中线的性质可得答案.
【详解】(1)证明:∵,
又
;
(2)①在中,∵
又∵为中点,,
则.
②在中,为的中点,
19.(1)
(2)见解析
(3)2
【分析】本题考查了平行四边形的判定与性质、三角形中位线定理、平行线的性质.
(1)由平行四边形的性质和平行线的判定和性质得出答案即可;
(2)由平行四边形的性质得,,再证是的中位线,得,,证出,,然后由平行四边形的判定即可得出结论;
(3)连接、、,由三角形的中位线定理以及平行四边形的判定和性质解答即可.
【详解】(1)∵四边形是平行四边形,
∴,
∴,
∵在中,,
∴;
(2)∵,,
∴是的中位线,
∴,,
∵H为FG的中点,
∴,
∴,,
∵四边形是平行四边形,
∴,,
∴,,
∴四边形是平行四边形;
(3)如图,连接,,
∵,H为FG的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴.
20.(1)的长为2或5
(2)矩形,详见解析
【分析】(1)利用勾股定理求得的长,再分和情况讨论即可求解;
(2)证明,推出,,再证明四边形是平行四边形,据此即可得到四边形是矩形.
【详解】(1)解:矩形中,,,
∴,
①当时,;
②当时,,
在中,,,
∴,
∴,
∴.
综上所述,CE的长为2或5;
(2)证明:∵四边形是矩形,
∴,,
∴,
在和中,
∴;
∴,,
∴,即,
∴,
∵平移得,
∴,,
∴,,
∴四边形是平行四边形,
∵,
∴,
∴,
∴四边形是矩形.
【点睛】本题考查了矩形的判定和性质,全等三角形的判定和性质,勾股定理,等腰三角形的性质等知识点.解题的关键是灵活运用所学知识解决问题.
21.(1)见解析
(2)见解析
(3)
【分析】(1)根据证即可;
(2)推出,根据平行四边形性质求出,推出,根据证即可;
(3)求出的周长,分为三种情况,①当P在上,Q在上,②当P在上,Q在上,③当P在上,Q在上,每种情况都等于的周长.
【详解】(1)解:四边形是平行四边形,
,
,
垂直平分,
,
在和中,
,
(),
;
(2)解:四边形是平行四边形,
,,
,
,
在和中,
,
();
(3)解:垂直平分,
,
,
,
,
的周长是
,
故的周长也是,
①当P在上,Q在上,
,
,
在和中
,
(),
,
②当P在上,Q在上,
,
,
,
,
在和中
,
(),
,
,
,
;
③当P在上,Q在上,
,
,
,
,
四边形是平行四边形,
,
,
,
在和中
,
(),
,
;
综上所述:m与n满足的数量关系是.
【点睛】本题考查了平行四边形的性质和判定,全等三角形的性质和判定,平行线的性质和判定的综合运用,掌握性质及判定方法,能根据和的不同位置进行分类讨论是解题的关键.
22.(1)见解析
(2)2.5或3
(3)能,t值为4.5或5或
【分析】(1)设,,,则,由勾股定理求出,即可得出结论;
(2)由的面积求出、、、的长;①当时,;②当时,;得出方程,解方程即可;
(3)由勾股定理可得,根据题意得出当点在上,即时,为等腰三角形,有3种可能:①;②;③;分别得出方程,解方程即可.
【详解】(1)证明:设,,,则,
,
,
,
,
是等腰三角形;
(2)解:,而,
,
则,,,,
由题意得:
若的边与平行,存在以下两种情况:
①当时,如图2,,,
,
,
,
,
,
;
②当时,如图3,同理得:,
,
,
若的边与平行时,值为2.5或3;
(3)解:能成为等腰三角形;
是的垂直平分线,,
,,
,
∴,
,
是的中位线,
,
由勾股定理得:,
①当时,是等腰三角形,
,
;
②当时,如图5,是等腰三角形,此时与重合,
;
③当时,是等腰三角形,
如图6,过点作于,交于,连接,
,
设,则,
在中,由勾股定理得:,
,
,
,
由勾股定理得:,
设,,
,
,
,
,
在中,,
,
,
,
,
综上,的值是或5或.
【点睛】本题是三角形的综合题,考查了勾股定理,等腰三角形的判定与性质,三角形的面积,完全平方公式,线段垂直平分线的性质,三角形的中位线定理,解方程等知识,本题有一定难度,需要进行分类讨论才能得出结果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
