圆柱的表面积专项突破(含答案)数学六年级下册苏教版
文档属性
| 名称 | 圆柱的表面积专项突破(含答案)数学六年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 495.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 10:36:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆柱的表面积专项突破-数学六年级下册苏教版
1.修建一个圆柱形的沼气池,底面直径是4米,深3米。在池的四壁与下底抹上水泥,抹水泥的部分面积是多少?
2.一个圆柱形铁皮油桶(有盖),底面周长是25.12分米,高是底面半径的,在这个油桶的外表面刷上一层防锈漆,刷防锈漆的面积是多少平方分米?
3.将一个圆柱沿底面直径把它纵切成两个半圆柱(如图所示),如果切面是边长为8厘米的正方形,那么原来圆柱体的表面积是多少平方厘米?
4.妈妈给小宝宝买了一顶蚊帐,做这样一顶蚊帐至少需要多少平方米的薄纱?(蚊帐有3个面,得数保留整数)
5.一顶圆柱形的厨师帽,高30厘米,帽顶直径20厘米。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
6.妈妈想给小雨的水壶做一个布套(如图),准备10平方分米的布料够吗?
7.有一个零件,如下图,零件的下面是一个大圆柱体,底面直径是6厘米,高10厘米。上面是一个小圆柱体,直径是4厘米,高5厘米。如果将这个零件接触空气的部分涂上防锈漆,你知道一共要涂多少平方厘米吗?
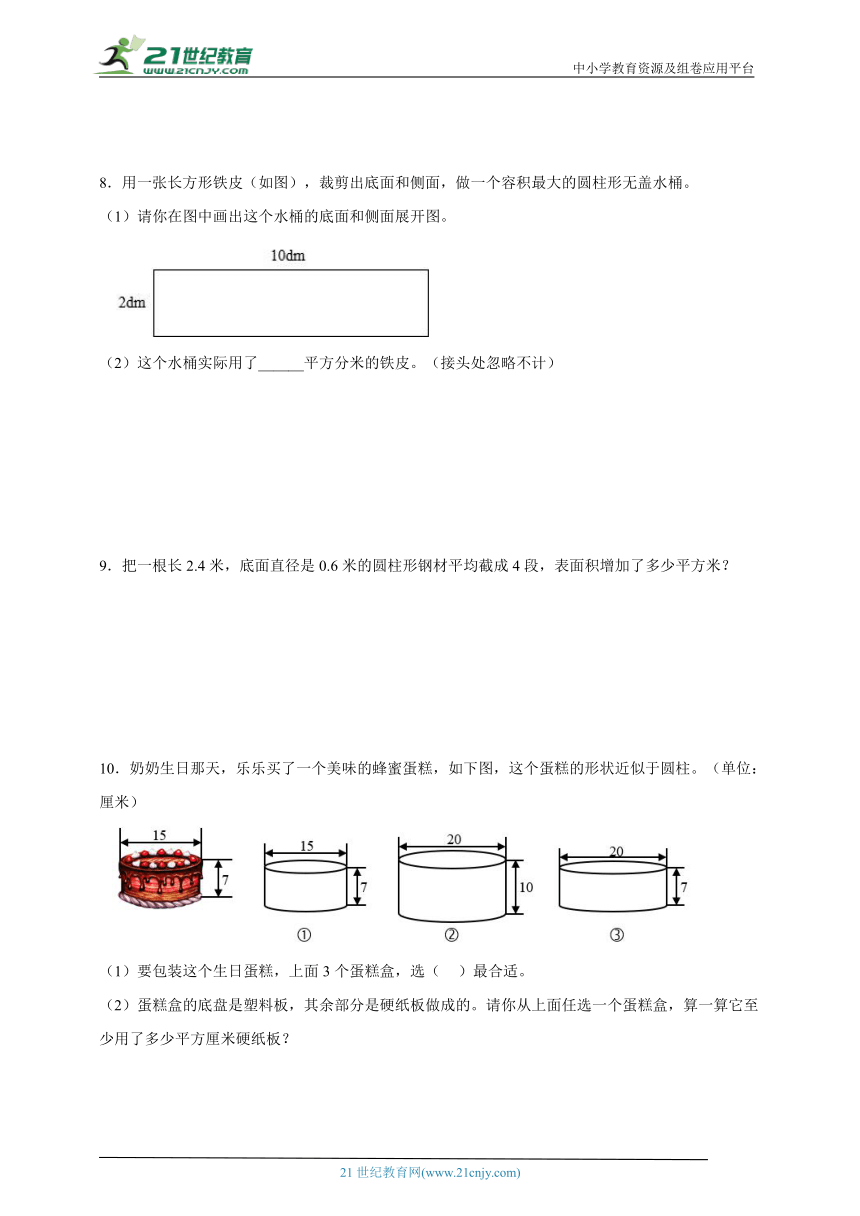
8.用一张长方形铁皮(如图),裁剪出底面和侧面,做一个容积最大的圆柱形无盖水桶。
(1)请你在图中画出这个水桶的底面和侧面展开图。
(2)这个水桶实际用了______平方分米的铁皮。(接头处忽略不计)
9.把一根长2.4米,底面直径是0.6米的圆柱形钢材平均截成4段,表面积增加了多少平方米?
10.奶奶生日那天,乐乐买了一个美味的蜂蜜蛋糕,如下图,这个蛋糕的形状近似于圆柱。(单位:厘米)
(1)要包装这个生日蛋糕,上面3个蛋糕盒,选( )最合适。
(2)蛋糕盒的底盘是塑料板,其余部分是硬纸板做成的。请你从上面任选一个蛋糕盒,算一算它至少用了多少平方厘米硬纸板?
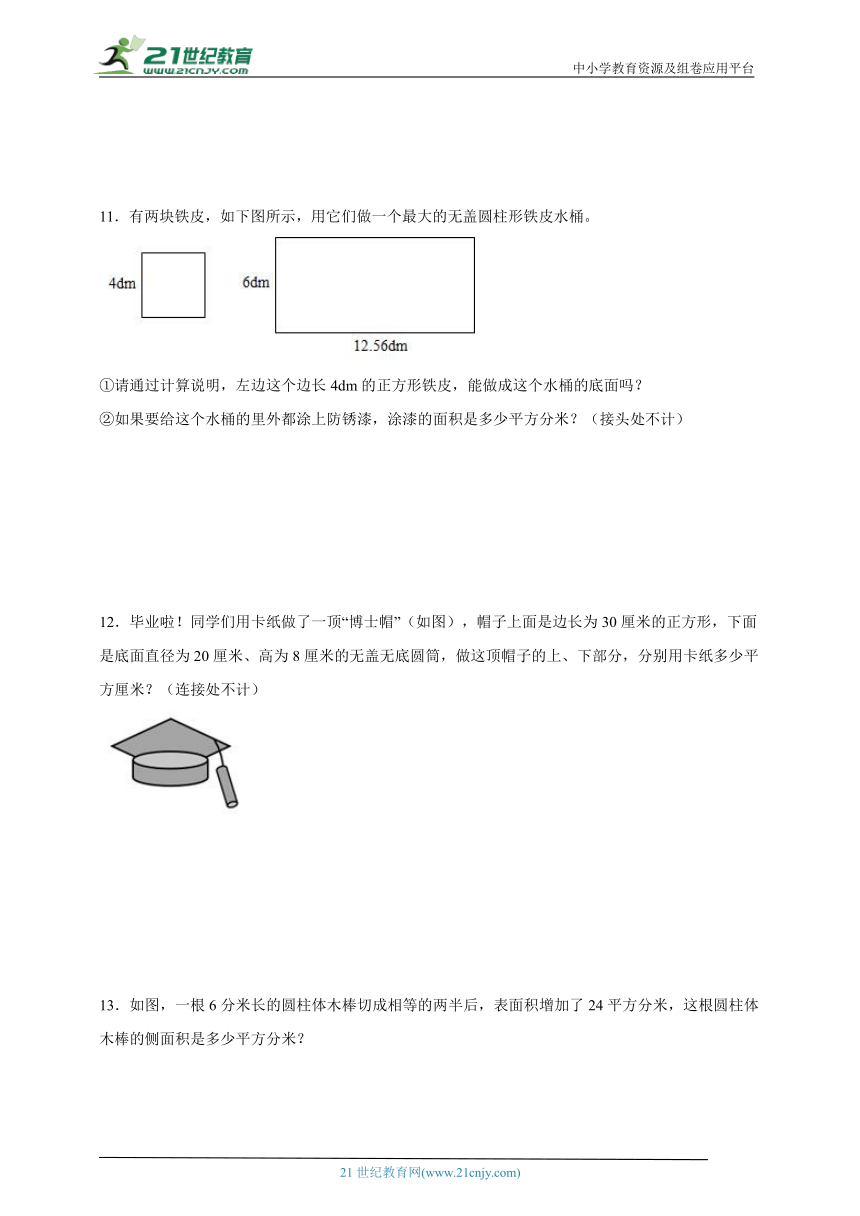
11.有两块铁皮,如下图所示,用它们做一个最大的无盖圆柱形铁皮水桶。
①请通过计算说明,左边这个边长4dm的正方形铁皮,能做成这个水桶的底面吗?
②如果要给这个水桶的里外都涂上防锈漆,涂漆的面积是多少平方分米?(接头处不计)
12.毕业啦!同学们用卡纸做了一顶“博士帽”(如图),帽子上面是边长为30厘米的正方形,下面是底面直径为20厘米、高为8厘米的无盖无底圆筒,做这顶帽子的上、下部分,分别用卡纸多少平方厘米?(连接处不计)
13.如图,一根6分米长的圆柱体木棒切成相等的两半后,表面积增加了24平方分米,这根圆柱体木棒的侧面积是多少平方分米?
14.如图是一个两层的六寸的生日蛋糕,已知底层直径是20厘米,高度是10厘米;上层直径是15厘米,高是6厘米,现在准备在它外表涂抹奶油(底部不涂),求该蛋糕需要涂抹奶油的面积。
15.将一个高是5分米的圆柱体的底面平均分成若干等份,切开后拼成一个近似的长方体的长是6.28厘米。这个圆柱体的表面积是多少平方厘米?体积是多少立方厘米?
16.下图是一个高为3厘米的圆柱侧面展开图,求这个圆柱的表面积。
17.有甲、乙两个圆柱,表面积都是90;底面积也相等,每个底面的面积都是15。如果把这两个圆柱接起来,成为一个大圆柱。
(1)这个大圆柱的侧面积是多少cm2?
(2)这个大圆柱的表面积是多少cm2?
18.如图,一个圆柱体木材被截去5cm后,圆柱的表面积减少了47.1cm2,求原来圆柱体的表面积是多少cm2?
19.一根圆柱形木材长2米,把它沿横截面截成相等的4段小圆柱形木材后,表面积增加了37.68平方厘米。原来这根圆柱形木材的体积是多少立方厘米?
20.王阿姨做了一个圆柱形抱枕,长80厘米,底面直径是18厘米,如果侧面用花布,两个底面用红布,至少需要花布多少平方厘米?红布呢?
21.如图所示的百宝箱,上部是一个圆柱的一半,下部是一个长50cm,宽40cm,高20cm的长方体,这个百宝箱的表面积是多少?
参考答案:
1.50.24平方米
【分析】由题意可知,抹水泥的部分面积是就是圆柱形沼气池的底面积与圆柱的侧面积的和,据此进行计算即可。
【详解】3.14×(4÷2)2+3.14×4×3
=3.14×4+3.14×12
=12.56+37.68
=50.24(平方米)
答:抹水泥的部分面积是50.24平方米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
2.351.68平方分米
【分析】根据圆的周长公式:C=2πr,把数代入求出底面圆的半径,即25.12÷3.14÷2=4(分米),由于高是底面半径的250%,单位“1”是底面半径的长度,单位“1”已知,用乘法,即4×250%=10(分米),外表面刷上一层防锈漆,则相当于求圆柱的表面积,根据圆柱的表面积公式:S=πdh+2πr2,把数代入公式即可求解。
【详解】25.12÷3.14÷2=4(分米)
4×250%=10(分米)
3.14×4×4×2+3.14×4×2×10
=100.48+251.2
=351.68(平方分米)
答:刷防锈漆的面积是351.68平方分米。
【点睛】本题主要考查圆柱的表面积公式,熟练掌握它的表面积公式并灵活运用。
3.301.44平方厘米
【分析】如图可知,圆柱纵切面底边对应的是圆柱底面圆的直径,高对应的是圆柱的高。切面为边长8厘米的正方形,说明圆柱底面圆的直径为8厘米,圆柱的高为8厘米。圆柱的表面积=底面圆面积×2+侧面积。底面圆面积=π×(8÷2)2,侧面积=π×8×8,据此求解。
【详解】底面积=π×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
侧面积=π×8×8
=3.14×64
=200.96(平方厘米)
50.24×2+200.96
=100.48+200.96
=301.44(平方厘米)
答:原来圆柱体的表面积是301.44平方厘米。
【点睛】本题主要考查圆柱体的表面积,关键要理解纵切截面与圆柱的对应关系。
4.4平方米
【分析】蚊帐有3个面组成,即圆柱侧面积的一半,底面的两个半圆可以组成一个圆;求做这样一顶蚊帐至少需要薄纱的面积,就是求侧面积的一半与一个底面积之和;根据圆柱侧面积公式S侧=πdh,圆柱的底面积公式S底=πr2,代入数据计算,计算结果要采用“进一法”保留整数。
【详解】蚊帐的侧面积:
3.14×1.2×1.5÷2
=3.14×0.9
=2.826(平方米)
蚊帐的底面积:
3.14×(1.2÷2)2
=3.14×0.36
=1.1304(平方米)
至少需要:
2.826+1.1304≈4(平方米)
答:做这样一顶蚊帐至少需要4平方米的薄纱。
【点睛】本题考查圆柱表面积公式的灵活运用,关键是从图中分析出图形是由哪些面组成,根据这些面的面积公式列式计算即可。
5.2200平方厘米
【分析】求做这样一顶帽子至少要用面料的面积,就是求圆柱形帽子的表面积。因为帽子没有下底,所以只需计算侧面积与一个底面积之和;根据圆柱侧面积公式S侧=πdh,圆柱的底面积公式S底=πr2,代入数据计算,计算结果要采用“进一法”保留整十数。
【详解】帽子的侧面积:
3.14×20×30
=62.8×30
=1884(平方厘米)
帽顶的面积:
3.14×(20÷2)2
=3.14×100
=314(平方厘米)
需要用的面积:
1884+314≈2200(平方厘米)
答:做这样一顶帽子至少要用2200平方厘米的面料。
【点睛】求圆柱的表面积时,要明确有几个底面或没有底面,灵活运用圆柱的表面积公式求解。
6.够
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式求出这个圆柱的表面积,然后与10平方分米进行比较即可。
【详解】3.14×10×20+3.14×(10÷2)2×2
=31.4×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(平方厘米)
10平方分米=1000平方厘米
785平方厘米<1000平方厘米
答:准备10平方分米的布料够。
【点睛】此题的解题关键是灵活运用圆柱的表面积公式解决实际的问题。
7.307.72平方厘米
【分析】观察图形可知,需要涂防锈漆的面积=上面圆柱的表面积+下面圆柱的表面积-两个上面圆柱的底面积,根据圆柱的表面积公式:S=2πr2+πdh,据此进行计算即可。
【详解】2×3.14×(6÷2)2+3.14×6×10
=56.52+188.4
=244.92(平方厘米)
2×3.14×(4÷2)2+3.14×4×5
=25.12+62.8
=87.92(平方厘米)
244.92+87.92-3.14×(4÷2)2×2
=332.84-25.12
=307.72(平方厘米)
答:一共要涂307.72平方厘米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
8.(1)见详解;(2)15.7
【分析】(1)要想做一个容积最大的圆柱形无盖水桶,有2种选择:①以长方形的宽为底面周长裁出一个圆,以剩下部分长方形的长为高围成一个圆柱;②以宽为底面直径和高,围成一个圆柱;根据长方形围成圆柱的原理,可知:卷成圆柱的底面周长的那条边越长,围成的圆柱的体积越大。
则可确定以长方形铁皮的宽为底面直径,即2分米,长方形铁皮的宽为圆柱的高,则底面周长是2×3.14=6.28(分米),2+6.28=8.28(分米),8.28<10,具备围成圆柱的条件;据此画出这个水桶的底面和侧面展开图。
(2)水桶的表面积是由一个圆和一个长方形组成,据此求出表面积为:3.14×(2÷2)2+6.28×2=15.7(平方分米)。
【详解】(1)底面直径是2分米,高是2分米,
底面周长是2×3.14=6.28(分米)
2+6.28=8.28(分米)
8.28<10,具备围成圆柱的条件。
如图:
(2)3.14×(2÷2)2+6.28×2
=3.14+12.56
=15.7(平方分米)
这个水桶实际用了15.7平方分米的铁皮。
【点睛】本题考查了圆柱的展开图和圆柱的表面积;其中要运用长方形围成圆柱的原理,有一定难度,需要经过仔细分析、比较。
9.1.6956平方米
【分析】根据题意,把一根圆柱形钢材平均截成4段,要截3次,每截一次增加2个面,共增加6个截面的面积;截面是圆柱的底面积,根据公式S=πr2,求出一个截面的面积,再乘6即是增加的表面积。
【详解】增加的面:
(4-1)×2
=3×2
=6(个)
增加的表面积:
3.14×(0.6÷2)2×6
=3.14×0.09×6
=0.2826×6
=1.6956(平方米)
答:表面积增加了1.6956平方米。
【点睛】本题考查圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,求出圆柱的底面积是解题的关键。
10.(1)②
(2)942平方厘米
【分析】(1)蛋糕的形状近似于圆柱,底面直径是15厘米,高是7厘米,所选蛋糕盒的尺寸应该在直径和高的长度上都大于蛋糕的尺寸,才能装下蛋糕又留有一定的空间,据此可以选择②号蛋糕盒;
(2)可以选择②号蛋糕盒来计算。因为底盘是塑料板,其余部分是硬纸板,所以,硬纸板的面积就等于一个底面积与侧面积的和;列综合算式为:3.14×(20÷2)2+3.14×20×10。
【详解】(1)要包装这个生日蛋糕,选择(②)最合适;
(2)3.14×(20÷2)2+3.14×20×10
=3.14×100+3.14×200
=314+628
=942(平方厘米)
答:②号蛋糕盒,至少用了942平方厘米的硬纸板。
【点睛】懂的结合日常生活现象选择蛋糕盒;明确蛋糕盒硬纸板的面积是由哪几部分组成的,是解题关键。
11.①能;计算见详解
②175.84平方分米
【分析】①只要水桶的底面直径不超过正方形的边长,就可做成这个水桶的底面,根据直径=周长÷π,列式计算即可。
②涂漆的面积=底面积×2+侧面积×2,据此列式解答。
【详解】①12.56÷3.14=4(分米)
答:能做成这个水桶的底面。
②4÷2=2(分米)
3.14×22×2+12.56×6×2
=3.14×4×2+150.72
=25.12+150.72
=175.84(平方分米)
答:涂漆的面积是175.84平方分米。
【点睛】关键是熟悉圆柱特征,掌握并灵活运用圆柱表面积公式。
12.上部分900平方厘米,下部分502.4平方厘米
【分析】根据正方形的面积公式:S=a2,圆柱的侧面积公式:S=πdh,把数据代入公式解答。
【详解】30×30=900(平方厘米)
3.14×20×8
=62.8×8
=502.4(平方厘米)
答:做这顶帽子的上部分用卡纸900平方厘米,下部分用卡纸502.4平方厘米。
【点睛】本题考查了正方体的面积、圆柱的侧面积,解题关键是熟记公式。
13.37.68平方分米
【分析】沿底面直径把它平均切成两半,则圆柱的表面积是增加了2个以圆柱的底面直径和高为边长的长方形的面的面积,已知增加的表面积为24平方分米,高为6分米,代入求出圆柱的底面直径,再根据圆柱的侧面积公式:S=,代入数据即可求出这根圆柱体木棒的侧面积。
【详解】24÷2÷6=2(分米)
3.14×2×6=37.68(平方分米)
答:这根圆柱体木棒的侧面积是37.68平方分米。
【点睛】抓住圆柱的切割特点,得出增加的面积是以圆的底面直径和高为边长的两个长方形的面的面积,是解决此类问题的关键。
14.1224.6平方厘米
【分析】求该蛋糕需要涂抹奶油的面积,是在求两个圆柱的表面积,但两个圆柱叠加后,减少的面积为上圆柱的两个底面积,另外下圆柱的底面不涂,所以最终相当于求下圆柱的侧面积加上一个底面积,再加上上层圆柱的侧面积,利用圆柱的侧面积公式和表面积公式即可得解。
【详解】3.14×15×6
=47.1×6
=282.6(平方厘米)
3.14×20×10+3.14×(20÷2)2
=62.8×10+3.14×102
=628+314
=942(平方厘米)
282.6+942=1224.6(平方厘米)
答:该蛋糕需要涂抹奶油的面积1224.6平方厘米。
【点睛】此题的解题关键是掌握两个圆柱叠加后总的表面积的变化情况,再利用圆柱的表面积公式求解。
15.表面积:87.92平方厘米;体积:62.8立方厘米
【分析】根据圆柱体积公式的推导过程可知:把一个圆柱体平均分成若干份,拼成一个近似长方体,拼成的长方体的长等于圆柱底面周长的一半;长方体的高等于圆柱的高;由此根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出圆柱底面的半径;再根据圆柱的表面积公式:底面积×2+侧面积,代入数据,求出圆柱的表面积;再根据圆柱的体积公式:体积=底面积×高;代入数据,即可解答。
【详解】半径:
6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米)
表面积:
3.14×22×2+3.14×2×2×5
=3.14×4×2+6.28×2×5
=12.56×2+12.56×5
=25.12+62.8
=87.92(平方厘米)
体积:
3.14×22×5
=3.14×4×5
=12.56×5
=62.8(立方厘米)
答:这个圆柱的表面积是87.92平方厘米,体积是62.8立方厘米。
【点睛】熟练掌握运用圆柱的表面积公式和体积公式解答,关键明确拼成的长方体的长是圆柱底面周长的一半是解答本题的关键。
16.25.12 cm
【分析】圆柱侧面沿高展开是一个长方形,长方形的长=圆柱底面周长,长方形的宽=圆柱的高,先求出底面半径,根据圆柱表面积=侧面积+底面积×2,列式计算即可。
【详解】6.28÷3.14÷2=1(cm)
3×6.28+2×3.14×12
=18.84+6.28
=25.12(cm )
答:这个圆柱的表面积时25.12 cm 。
【点睛】关键是熟悉圆柱特征,掌握圆柱表面积公式,圆柱侧面积=底面周长×高。
17.(1)120
(2)150
【分析】(1)用一个圆柱的表面积减去两个底面积就是一个圆柱的侧面积,乘2即可求出大圆柱的侧面积;
(2)用大圆柱的侧面积加上两个底面积就是大圆柱的表面积。
【详解】(1)(90-15×2)×2
=(90-30)×2
=60×2
=120()
答:这个大圆柱的侧面积是120cm2。
(2)120+15×2
=120+30
=150()
答:这个大圆柱的表面积是150cm2。
【点睛】本题考查圆柱的表面积和侧面积,解答本题的关键是掌握圆柱的表面积和侧面积计算公式。
18.202.53cm2
【分析】通过观察图形可知,把这个圆柱体木材截去5cm,圆柱的表面积减少了47.1cm2,表面积减少的是高5cm的圆柱的侧面积,根据圆柱的侧面积公式:,据此可以求出圆柱的底面周长,再根据圆柱的表面积公式:,把数据代入公式解答。
【详解】47.1÷5=9.42(cm)
9.42×20+3.14×(9.42÷3.14÷2)2×2
=188.4+3.14×2.25×2
=188.4+14.13
=202.53(cm2)
答:原来圆柱体的表面积是202.53cm2。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
19.1256立方厘米
【分析】把圆柱截成4段,需要截4-1=3次,每截1次表面积就增加2个圆柱的底面的面积,所以一共增加了3×2=6个圆柱的底面的面积,由此利用增加的表面积求出这个圆柱的底面积,再利用圆柱的体积公式即可求出圆木的体积。
【详解】2米=200厘米,
(4-1)×2=6(个)
37.68÷6×200
=6.28×200
=1256(立方厘米)
答:原来这根圆柱形木材的体积是1256立方厘米。
【点睛】抓住圆柱切割小圆柱的方法,得出表面积增加的面的情况,是解决此类问题的关键。
20.花布4521.6平方厘米,红布508.68平方厘米
【分析】求所需花布的面积就是求圆柱的侧面积,求红布的面积即两个底面积之和,根据圆柱的侧面积=底面周长×高,圆柱的底面积公式:S=πr ,代入数据即可解答。
【详解】花布:3.14×18×80
=56.52×80
=4521.6(平方厘米)
红布:3.14×(18÷2) ×2
=254.34×2
=508.68(平方厘米)
答:至少需要花布4521.6平方厘米,红布508.68平方厘米。
【点睛】此题考查的是圆柱的表面积的应用,熟记公式是解题关键。
21.9996平方厘米
【分析】这个图形的表面积包含了圆柱的半个侧面积,以及一个底面积,同时还要加上长方体前面、后面、左面、右面和下面5个面的面积。
【详解】50×40+50×20×2+40×20×2+3.14×(40÷2)+3.14×40×50÷2
=2000+2000+1600+3.14×400+125.6×50÷2
=4000+1600+1256+6280÷2
=6856+3140
=9996(平方厘米)
答:百宝箱的表面积是9996平方厘米。
【点睛】本题考查组合图形的表面积,找准表面积是由哪些部分组成的是解题关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱的表面积专项突破-数学六年级下册苏教版
1.修建一个圆柱形的沼气池,底面直径是4米,深3米。在池的四壁与下底抹上水泥,抹水泥的部分面积是多少?
2.一个圆柱形铁皮油桶(有盖),底面周长是25.12分米,高是底面半径的,在这个油桶的外表面刷上一层防锈漆,刷防锈漆的面积是多少平方分米?
3.将一个圆柱沿底面直径把它纵切成两个半圆柱(如图所示),如果切面是边长为8厘米的正方形,那么原来圆柱体的表面积是多少平方厘米?
4.妈妈给小宝宝买了一顶蚊帐,做这样一顶蚊帐至少需要多少平方米的薄纱?(蚊帐有3个面,得数保留整数)
5.一顶圆柱形的厨师帽,高30厘米,帽顶直径20厘米。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
6.妈妈想给小雨的水壶做一个布套(如图),准备10平方分米的布料够吗?
7.有一个零件,如下图,零件的下面是一个大圆柱体,底面直径是6厘米,高10厘米。上面是一个小圆柱体,直径是4厘米,高5厘米。如果将这个零件接触空气的部分涂上防锈漆,你知道一共要涂多少平方厘米吗?
8.用一张长方形铁皮(如图),裁剪出底面和侧面,做一个容积最大的圆柱形无盖水桶。
(1)请你在图中画出这个水桶的底面和侧面展开图。
(2)这个水桶实际用了______平方分米的铁皮。(接头处忽略不计)
9.把一根长2.4米,底面直径是0.6米的圆柱形钢材平均截成4段,表面积增加了多少平方米?
10.奶奶生日那天,乐乐买了一个美味的蜂蜜蛋糕,如下图,这个蛋糕的形状近似于圆柱。(单位:厘米)
(1)要包装这个生日蛋糕,上面3个蛋糕盒,选( )最合适。
(2)蛋糕盒的底盘是塑料板,其余部分是硬纸板做成的。请你从上面任选一个蛋糕盒,算一算它至少用了多少平方厘米硬纸板?
11.有两块铁皮,如下图所示,用它们做一个最大的无盖圆柱形铁皮水桶。
①请通过计算说明,左边这个边长4dm的正方形铁皮,能做成这个水桶的底面吗?
②如果要给这个水桶的里外都涂上防锈漆,涂漆的面积是多少平方分米?(接头处不计)
12.毕业啦!同学们用卡纸做了一顶“博士帽”(如图),帽子上面是边长为30厘米的正方形,下面是底面直径为20厘米、高为8厘米的无盖无底圆筒,做这顶帽子的上、下部分,分别用卡纸多少平方厘米?(连接处不计)
13.如图,一根6分米长的圆柱体木棒切成相等的两半后,表面积增加了24平方分米,这根圆柱体木棒的侧面积是多少平方分米?
14.如图是一个两层的六寸的生日蛋糕,已知底层直径是20厘米,高度是10厘米;上层直径是15厘米,高是6厘米,现在准备在它外表涂抹奶油(底部不涂),求该蛋糕需要涂抹奶油的面积。
15.将一个高是5分米的圆柱体的底面平均分成若干等份,切开后拼成一个近似的长方体的长是6.28厘米。这个圆柱体的表面积是多少平方厘米?体积是多少立方厘米?
16.下图是一个高为3厘米的圆柱侧面展开图,求这个圆柱的表面积。
17.有甲、乙两个圆柱,表面积都是90;底面积也相等,每个底面的面积都是15。如果把这两个圆柱接起来,成为一个大圆柱。
(1)这个大圆柱的侧面积是多少cm2?
(2)这个大圆柱的表面积是多少cm2?
18.如图,一个圆柱体木材被截去5cm后,圆柱的表面积减少了47.1cm2,求原来圆柱体的表面积是多少cm2?
19.一根圆柱形木材长2米,把它沿横截面截成相等的4段小圆柱形木材后,表面积增加了37.68平方厘米。原来这根圆柱形木材的体积是多少立方厘米?
20.王阿姨做了一个圆柱形抱枕,长80厘米,底面直径是18厘米,如果侧面用花布,两个底面用红布,至少需要花布多少平方厘米?红布呢?
21.如图所示的百宝箱,上部是一个圆柱的一半,下部是一个长50cm,宽40cm,高20cm的长方体,这个百宝箱的表面积是多少?
参考答案:
1.50.24平方米
【分析】由题意可知,抹水泥的部分面积是就是圆柱形沼气池的底面积与圆柱的侧面积的和,据此进行计算即可。
【详解】3.14×(4÷2)2+3.14×4×3
=3.14×4+3.14×12
=12.56+37.68
=50.24(平方米)
答:抹水泥的部分面积是50.24平方米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
2.351.68平方分米
【分析】根据圆的周长公式:C=2πr,把数代入求出底面圆的半径,即25.12÷3.14÷2=4(分米),由于高是底面半径的250%,单位“1”是底面半径的长度,单位“1”已知,用乘法,即4×250%=10(分米),外表面刷上一层防锈漆,则相当于求圆柱的表面积,根据圆柱的表面积公式:S=πdh+2πr2,把数代入公式即可求解。
【详解】25.12÷3.14÷2=4(分米)
4×250%=10(分米)
3.14×4×4×2+3.14×4×2×10
=100.48+251.2
=351.68(平方分米)
答:刷防锈漆的面积是351.68平方分米。
【点睛】本题主要考查圆柱的表面积公式,熟练掌握它的表面积公式并灵活运用。
3.301.44平方厘米
【分析】如图可知,圆柱纵切面底边对应的是圆柱底面圆的直径,高对应的是圆柱的高。切面为边长8厘米的正方形,说明圆柱底面圆的直径为8厘米,圆柱的高为8厘米。圆柱的表面积=底面圆面积×2+侧面积。底面圆面积=π×(8÷2)2,侧面积=π×8×8,据此求解。
【详解】底面积=π×(8÷2)2
=3.14×42
=3.14×16
=50.24(平方厘米)
侧面积=π×8×8
=3.14×64
=200.96(平方厘米)
50.24×2+200.96
=100.48+200.96
=301.44(平方厘米)
答:原来圆柱体的表面积是301.44平方厘米。
【点睛】本题主要考查圆柱体的表面积,关键要理解纵切截面与圆柱的对应关系。
4.4平方米
【分析】蚊帐有3个面组成,即圆柱侧面积的一半,底面的两个半圆可以组成一个圆;求做这样一顶蚊帐至少需要薄纱的面积,就是求侧面积的一半与一个底面积之和;根据圆柱侧面积公式S侧=πdh,圆柱的底面积公式S底=πr2,代入数据计算,计算结果要采用“进一法”保留整数。
【详解】蚊帐的侧面积:
3.14×1.2×1.5÷2
=3.14×0.9
=2.826(平方米)
蚊帐的底面积:
3.14×(1.2÷2)2
=3.14×0.36
=1.1304(平方米)
至少需要:
2.826+1.1304≈4(平方米)
答:做这样一顶蚊帐至少需要4平方米的薄纱。
【点睛】本题考查圆柱表面积公式的灵活运用,关键是从图中分析出图形是由哪些面组成,根据这些面的面积公式列式计算即可。
5.2200平方厘米
【分析】求做这样一顶帽子至少要用面料的面积,就是求圆柱形帽子的表面积。因为帽子没有下底,所以只需计算侧面积与一个底面积之和;根据圆柱侧面积公式S侧=πdh,圆柱的底面积公式S底=πr2,代入数据计算,计算结果要采用“进一法”保留整十数。
【详解】帽子的侧面积:
3.14×20×30
=62.8×30
=1884(平方厘米)
帽顶的面积:
3.14×(20÷2)2
=3.14×100
=314(平方厘米)
需要用的面积:
1884+314≈2200(平方厘米)
答:做这样一顶帽子至少要用2200平方厘米的面料。
【点睛】求圆柱的表面积时,要明确有几个底面或没有底面,灵活运用圆柱的表面积公式求解。
6.够
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式求出这个圆柱的表面积,然后与10平方分米进行比较即可。
【详解】3.14×10×20+3.14×(10÷2)2×2
=31.4×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(平方厘米)
10平方分米=1000平方厘米
785平方厘米<1000平方厘米
答:准备10平方分米的布料够。
【点睛】此题的解题关键是灵活运用圆柱的表面积公式解决实际的问题。
7.307.72平方厘米
【分析】观察图形可知,需要涂防锈漆的面积=上面圆柱的表面积+下面圆柱的表面积-两个上面圆柱的底面积,根据圆柱的表面积公式:S=2πr2+πdh,据此进行计算即可。
【详解】2×3.14×(6÷2)2+3.14×6×10
=56.52+188.4
=244.92(平方厘米)
2×3.14×(4÷2)2+3.14×4×5
=25.12+62.8
=87.92(平方厘米)
244.92+87.92-3.14×(4÷2)2×2
=332.84-25.12
=307.72(平方厘米)
答:一共要涂307.72平方厘米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
8.(1)见详解;(2)15.7
【分析】(1)要想做一个容积最大的圆柱形无盖水桶,有2种选择:①以长方形的宽为底面周长裁出一个圆,以剩下部分长方形的长为高围成一个圆柱;②以宽为底面直径和高,围成一个圆柱;根据长方形围成圆柱的原理,可知:卷成圆柱的底面周长的那条边越长,围成的圆柱的体积越大。
则可确定以长方形铁皮的宽为底面直径,即2分米,长方形铁皮的宽为圆柱的高,则底面周长是2×3.14=6.28(分米),2+6.28=8.28(分米),8.28<10,具备围成圆柱的条件;据此画出这个水桶的底面和侧面展开图。
(2)水桶的表面积是由一个圆和一个长方形组成,据此求出表面积为:3.14×(2÷2)2+6.28×2=15.7(平方分米)。
【详解】(1)底面直径是2分米,高是2分米,
底面周长是2×3.14=6.28(分米)
2+6.28=8.28(分米)
8.28<10,具备围成圆柱的条件。
如图:
(2)3.14×(2÷2)2+6.28×2
=3.14+12.56
=15.7(平方分米)
这个水桶实际用了15.7平方分米的铁皮。
【点睛】本题考查了圆柱的展开图和圆柱的表面积;其中要运用长方形围成圆柱的原理,有一定难度,需要经过仔细分析、比较。
9.1.6956平方米
【分析】根据题意,把一根圆柱形钢材平均截成4段,要截3次,每截一次增加2个面,共增加6个截面的面积;截面是圆柱的底面积,根据公式S=πr2,求出一个截面的面积,再乘6即是增加的表面积。
【详解】增加的面:
(4-1)×2
=3×2
=6(个)
增加的表面积:
3.14×(0.6÷2)2×6
=3.14×0.09×6
=0.2826×6
=1.6956(平方米)
答:表面积增加了1.6956平方米。
【点睛】本题考查圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,求出圆柱的底面积是解题的关键。
10.(1)②
(2)942平方厘米
【分析】(1)蛋糕的形状近似于圆柱,底面直径是15厘米,高是7厘米,所选蛋糕盒的尺寸应该在直径和高的长度上都大于蛋糕的尺寸,才能装下蛋糕又留有一定的空间,据此可以选择②号蛋糕盒;
(2)可以选择②号蛋糕盒来计算。因为底盘是塑料板,其余部分是硬纸板,所以,硬纸板的面积就等于一个底面积与侧面积的和;列综合算式为:3.14×(20÷2)2+3.14×20×10。
【详解】(1)要包装这个生日蛋糕,选择(②)最合适;
(2)3.14×(20÷2)2+3.14×20×10
=3.14×100+3.14×200
=314+628
=942(平方厘米)
答:②号蛋糕盒,至少用了942平方厘米的硬纸板。
【点睛】懂的结合日常生活现象选择蛋糕盒;明确蛋糕盒硬纸板的面积是由哪几部分组成的,是解题关键。
11.①能;计算见详解
②175.84平方分米
【分析】①只要水桶的底面直径不超过正方形的边长,就可做成这个水桶的底面,根据直径=周长÷π,列式计算即可。
②涂漆的面积=底面积×2+侧面积×2,据此列式解答。
【详解】①12.56÷3.14=4(分米)
答:能做成这个水桶的底面。
②4÷2=2(分米)
3.14×22×2+12.56×6×2
=3.14×4×2+150.72
=25.12+150.72
=175.84(平方分米)
答:涂漆的面积是175.84平方分米。
【点睛】关键是熟悉圆柱特征,掌握并灵活运用圆柱表面积公式。
12.上部分900平方厘米,下部分502.4平方厘米
【分析】根据正方形的面积公式:S=a2,圆柱的侧面积公式:S=πdh,把数据代入公式解答。
【详解】30×30=900(平方厘米)
3.14×20×8
=62.8×8
=502.4(平方厘米)
答:做这顶帽子的上部分用卡纸900平方厘米,下部分用卡纸502.4平方厘米。
【点睛】本题考查了正方体的面积、圆柱的侧面积,解题关键是熟记公式。
13.37.68平方分米
【分析】沿底面直径把它平均切成两半,则圆柱的表面积是增加了2个以圆柱的底面直径和高为边长的长方形的面的面积,已知增加的表面积为24平方分米,高为6分米,代入求出圆柱的底面直径,再根据圆柱的侧面积公式:S=,代入数据即可求出这根圆柱体木棒的侧面积。
【详解】24÷2÷6=2(分米)
3.14×2×6=37.68(平方分米)
答:这根圆柱体木棒的侧面积是37.68平方分米。
【点睛】抓住圆柱的切割特点,得出增加的面积是以圆的底面直径和高为边长的两个长方形的面的面积,是解决此类问题的关键。
14.1224.6平方厘米
【分析】求该蛋糕需要涂抹奶油的面积,是在求两个圆柱的表面积,但两个圆柱叠加后,减少的面积为上圆柱的两个底面积,另外下圆柱的底面不涂,所以最终相当于求下圆柱的侧面积加上一个底面积,再加上上层圆柱的侧面积,利用圆柱的侧面积公式和表面积公式即可得解。
【详解】3.14×15×6
=47.1×6
=282.6(平方厘米)
3.14×20×10+3.14×(20÷2)2
=62.8×10+3.14×102
=628+314
=942(平方厘米)
282.6+942=1224.6(平方厘米)
答:该蛋糕需要涂抹奶油的面积1224.6平方厘米。
【点睛】此题的解题关键是掌握两个圆柱叠加后总的表面积的变化情况,再利用圆柱的表面积公式求解。
15.表面积:87.92平方厘米;体积:62.8立方厘米
【分析】根据圆柱体积公式的推导过程可知:把一个圆柱体平均分成若干份,拼成一个近似长方体,拼成的长方体的长等于圆柱底面周长的一半;长方体的高等于圆柱的高;由此根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出圆柱底面的半径;再根据圆柱的表面积公式:底面积×2+侧面积,代入数据,求出圆柱的表面积;再根据圆柱的体积公式:体积=底面积×高;代入数据,即可解答。
【详解】半径:
6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米)
表面积:
3.14×22×2+3.14×2×2×5
=3.14×4×2+6.28×2×5
=12.56×2+12.56×5
=25.12+62.8
=87.92(平方厘米)
体积:
3.14×22×5
=3.14×4×5
=12.56×5
=62.8(立方厘米)
答:这个圆柱的表面积是87.92平方厘米,体积是62.8立方厘米。
【点睛】熟练掌握运用圆柱的表面积公式和体积公式解答,关键明确拼成的长方体的长是圆柱底面周长的一半是解答本题的关键。
16.25.12 cm
【分析】圆柱侧面沿高展开是一个长方形,长方形的长=圆柱底面周长,长方形的宽=圆柱的高,先求出底面半径,根据圆柱表面积=侧面积+底面积×2,列式计算即可。
【详解】6.28÷3.14÷2=1(cm)
3×6.28+2×3.14×12
=18.84+6.28
=25.12(cm )
答:这个圆柱的表面积时25.12 cm 。
【点睛】关键是熟悉圆柱特征,掌握圆柱表面积公式,圆柱侧面积=底面周长×高。
17.(1)120
(2)150
【分析】(1)用一个圆柱的表面积减去两个底面积就是一个圆柱的侧面积,乘2即可求出大圆柱的侧面积;
(2)用大圆柱的侧面积加上两个底面积就是大圆柱的表面积。
【详解】(1)(90-15×2)×2
=(90-30)×2
=60×2
=120()
答:这个大圆柱的侧面积是120cm2。
(2)120+15×2
=120+30
=150()
答:这个大圆柱的表面积是150cm2。
【点睛】本题考查圆柱的表面积和侧面积,解答本题的关键是掌握圆柱的表面积和侧面积计算公式。
18.202.53cm2
【分析】通过观察图形可知,把这个圆柱体木材截去5cm,圆柱的表面积减少了47.1cm2,表面积减少的是高5cm的圆柱的侧面积,根据圆柱的侧面积公式:,据此可以求出圆柱的底面周长,再根据圆柱的表面积公式:,把数据代入公式解答。
【详解】47.1÷5=9.42(cm)
9.42×20+3.14×(9.42÷3.14÷2)2×2
=188.4+3.14×2.25×2
=188.4+14.13
=202.53(cm2)
答:原来圆柱体的表面积是202.53cm2。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
19.1256立方厘米
【分析】把圆柱截成4段,需要截4-1=3次,每截1次表面积就增加2个圆柱的底面的面积,所以一共增加了3×2=6个圆柱的底面的面积,由此利用增加的表面积求出这个圆柱的底面积,再利用圆柱的体积公式即可求出圆木的体积。
【详解】2米=200厘米,
(4-1)×2=6(个)
37.68÷6×200
=6.28×200
=1256(立方厘米)
答:原来这根圆柱形木材的体积是1256立方厘米。
【点睛】抓住圆柱切割小圆柱的方法,得出表面积增加的面的情况,是解决此类问题的关键。
20.花布4521.6平方厘米,红布508.68平方厘米
【分析】求所需花布的面积就是求圆柱的侧面积,求红布的面积即两个底面积之和,根据圆柱的侧面积=底面周长×高,圆柱的底面积公式:S=πr ,代入数据即可解答。
【详解】花布:3.14×18×80
=56.52×80
=4521.6(平方厘米)
红布:3.14×(18÷2) ×2
=254.34×2
=508.68(平方厘米)
答:至少需要花布4521.6平方厘米,红布508.68平方厘米。
【点睛】此题考查的是圆柱的表面积的应用,熟记公式是解题关键。
21.9996平方厘米
【分析】这个图形的表面积包含了圆柱的半个侧面积,以及一个底面积,同时还要加上长方体前面、后面、左面、右面和下面5个面的面积。
【详解】50×40+50×20×2+40×20×2+3.14×(40÷2)+3.14×40×50÷2
=2000+2000+1600+3.14×400+125.6×50÷2
=4000+1600+1256+6280÷2
=6856+3140
=9996(平方厘米)
答:百宝箱的表面积是9996平方厘米。
【点睛】本题考查组合图形的表面积,找准表面积是由哪些部分组成的是解题关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
