长方体和正方体专项突破(含答案)数学五年级下册人教版
文档属性
| 名称 | 长方体和正方体专项突破(含答案)数学五年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 421.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 11:55:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
长方体和正方体专项突破-数学五年级下册人教版
1.一个表面积是96平方厘米的正方体,把它截成5个完全相同的长方体后,表面积增加了多少平方厘米?
2.一个房间长6米,宽3.5米,高3米,门窗面积8平方米,现在要把这个房间的四壁和顶面粉刷水泥,如果每平方米用涂料0.25千克,一共需要涂料多少千克?
3.一种长方体通风管,长2米,宽和高都是10厘米,做30节这样的通风管至少需要铁皮多少平方分米?
4.一个游泳池,长是40米,宽是25米,深是2.2米。
(1)这个游泳池的占地面积是多少?
(2)建造这个游泳池需挖土多少?
(3)要在它的四壁和底面铺上瓷砖,铺瓷砖的面积是多少?
5.一个无盖长方体玻璃容器的长是20厘米,宽和高都是10厘米。
(1)做这个玻璃容器至少需要玻璃多少平方分米?(玻璃厚度忽略不计)
(2)在这个长方体容器中加入一些水,来测量石头的体积,具体过程如图所示,这块石头的体积大约是多少立方厘米?
6.夏大妈家的柜式空调长0.5米,宽0.3米,高1.6米,为了防灰尘,夏大妈准备用布做一只长方体套子把空调罩起来,请你帮她算下,做这只套子至少需要用多少平方米的布?(接头处忽略不计)
7.一个长方体油箱,长8分米,宽6分米,高5分米。
(1)做这个油箱至少需要多少平方分米的铁皮?
(2)如果每升油6.5元,加满这个油箱需多少元?
8.一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(1)做这个鱼缸至少需要玻璃多少平方分米?
(2)鱼缸里有一些水,往水里放入一些鹅卵石,水面上升了0.3分米,鹅卵石的体积一共是多少立方分米?
9.一块长方形铁皮,如图,从四个角各切掉一个边长为x厘米的正方形,焊接成一个无盖盒子。
(1)当x=5时,焊接无盖盒子用了多少铁皮?
(2)当x=5时,这个盒子的占地面积是多少?
(3)当x=5时,这个盒子的容积是多少?
(4)x可取的数值很多,在这些数值中,x=5时的盒子容积是最小的吗?请回答并写出过程。
10.用一根长48分米的铁丝做一个长方体的框架,使它的高为8分米,底面是一个正方形(如图),再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸?
11.在一个长3分米,宽24厘米,高22厘米的玻璃缸中,水深18厘米,水接触玻璃的面积有多大?将一个棱长15厘米的正方体铁块放入水中后,缸中的水会溢出来吗?(通过计算来说明)
12.剧院大门前有10级台阶,每级台阶长16米,宽0.3米,高0.2米。
(1)10级这样的台阶共占地多少平方米?
(2)给这些台阶贴上地砖,至少需要多少平方米的地砖?
13.挖一个长8米、宽6米、深2米的蓄水池。
(1)这个蓄水池的占地面积是多少平方米?
(2)如果给这个蓄水池的四周和底部抹上水泥,抹水泥部分的面积是多少平方米?
(3)这个水池最多能蓄水多少吨?(1立方米的水重1吨)
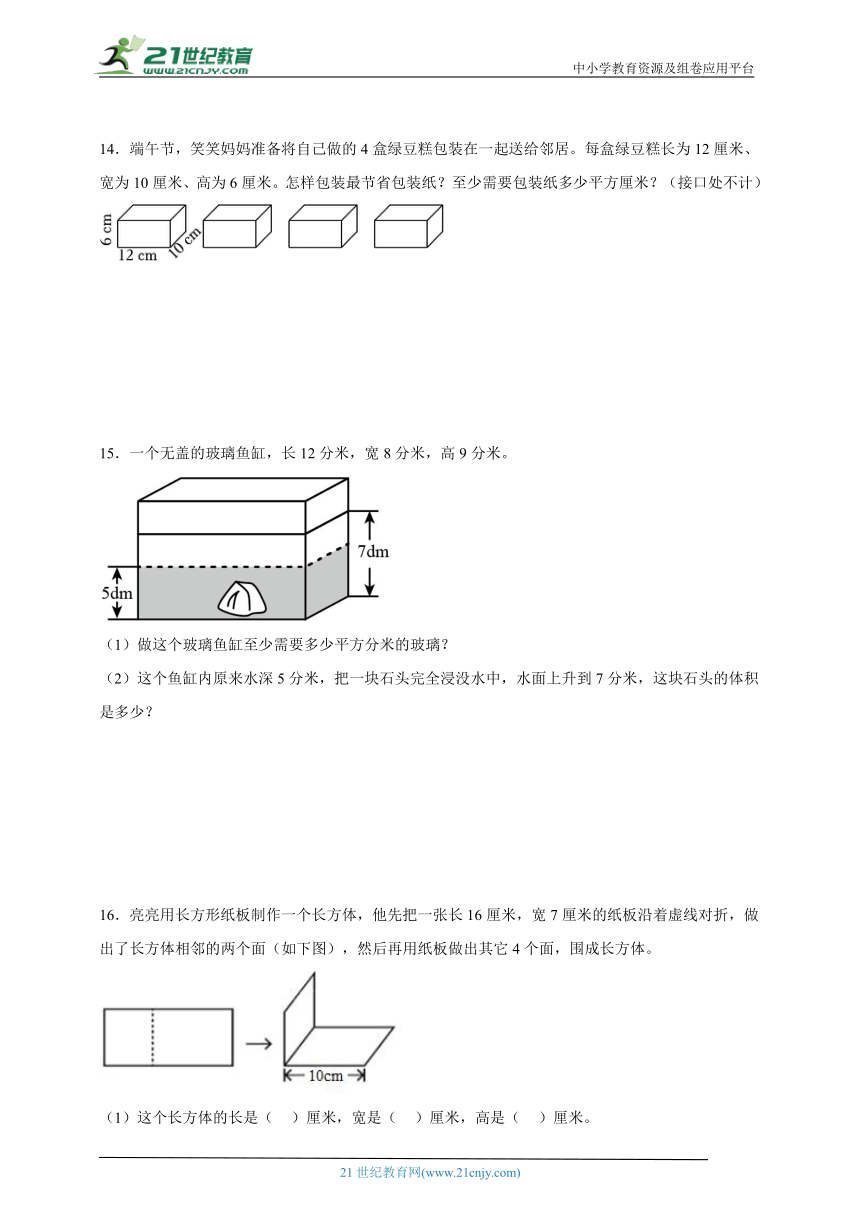
14.端午节,笑笑妈妈准备将自己做的4盒绿豆糕包装在一起送给邻居。每盒绿豆糕长为12厘米、宽为10厘米、高为6厘米。怎样包装最节省包装纸?至少需要包装纸多少平方厘米?(接口处不计)
15.一个无盖的玻璃鱼缸,长12分米,宽8分米,高9分米。
(1)做这个玻璃鱼缸至少需要多少平方分米的玻璃?
(2)这个鱼缸内原来水深5分米,把一块石头完全浸没水中,水面上升到7分米,这块石头的体积是多少?
16.亮亮用长方形纸板制作一个长方体,他先把一张长16厘米,宽7厘米的纸板沿着虚线对折,做出了长方体相邻的两个面(如下图),然后再用纸板做出其它4个面,围成长方体。
(1)这个长方体的长是( )厘米,宽是( )厘米,高是( )厘米。
(2)计算这个长方体的右面、上面、前面的面积各是多少平方厘米?
17.一个密封的长方体容器,从里面量长4dm,宽3dm,高6dm,水深4dm。
(1)这个长方体容器的容积是多少dm3?
(2)水与容器的接触面积是多少dm2?
(3)如果以这个长方体的前面为底面把长方体容器倒放在桌面上,这时水深是多少?
18.有一张长方体表面展开图(如图)。
(1)这个长方体的表面积是多少平方厘米?
(2)折成长方体后它的体积是多少立方厘米?
19.把下图的木块平均分成两块,两块木块的表面积的和比原来木块的表面积增加了多少平方厘米?
20.一个高40厘米,底面是正方形的长方体,如果高增加5厘米,表面积就增加80平方厘米,求原来长方体的表面积和体积各是多少?
21.—个底面是正方形的长方体,如果把高减少4cm,就变成了一个正方体。表面积相应减少96cm2,原来长方体的体积是多少?
参考答案:
1.128平方厘米
【分析】根据正方体的表面积=棱长×棱长×6,已知正方体的表面积可以求出一个面的面积,把这个正方体截成5个完全相同的长方体后,表面积增加了(2×4)个截面的面积,把数据代入公式解答。
【详解】96÷6×(2×4)
=16×8
=128(平方厘米)
答:表面积增加了128平方厘米。
2.17.5千克
【分析】根据长方体表面积的计算方法,首先分清求的是哪5个面的总面积,即上面、前后面、左右面;再减去门窗的面积,求出需要粉刷的面积;然后根据乘法的意义求出一共需要涂料的质量。
【详解】6×3.5+6×3×2+3.5×3×2-8
=21+36+21-8
=70(平方米)
70×0.25=17.5(千克)
答:一共需要涂料17.5千克。
3.2400平方分米
【分析】长方体通风管只有4个面,用长×宽×2+长×高×2,求出一个通风管的表面积,再乘30即可。
【详解】2米=20分米
10厘米=1分米
20×1×2+20×1×2
=40+40
=80(平方分米)
80×30=2400(平方分米)
答:做30节这样的通风管至少需要铁皮2400平方分米。
4.(1)1000平方米
(2)2200立方米
(3)1286平方米
【分析】(1)根据长方形的面积公式:S=ab,即用40乘25即可求出这个游泳池的占地面积;
(2)根据长方体的体积公式:V=abh,据此代入数值进行求出建造这个游泳池需挖土多少;
(3)要在它的四壁和底面铺上瓷砖,则瓷砖的面积等于长方体五个面的面积(除去上面),这五个面的面积=(长×高+宽×高)×2+长×宽,据此进行计算即可。
【详解】(1)40×25=1000(平方米)
答:这个游泳池的占地面积是1000平方米。
(2)40×25×2.2
=1000×2.2
=2200(立方米)
答:建造这个游泳池需挖土2200立方米。
(3)(40×2.2+25×2.2)×2+40×25
=(88+55)×2+1000
=143×2+1000
=286+1000
=1286(平方米)
答:铺瓷砖的面积是1286平方米。
【点睛】本题考查长方体的体积和表面积,熟记公式是解题的关键。
5.(1)8平方分米
(2)800立方厘米
【分析】(1)根据题意,已知无盖长方体玻璃容器的长、宽、高,求做这个玻璃容器至少需要玻璃的面积,就是求长方体的下面、前后面、左右面共5个面的面积;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,再根据进率“1平方分米=100平方厘米”换算单位即可。
(2)从图中可知,取出石头后水面下降4厘米,那么水下降部分的体积等于这块石头的体积;水下降部分是一个长20厘米、宽10厘米、高4厘米的长方体,根据长方体的体积=长×宽×高,代入数据计算,即可求出这块石头的体积。
【详解】(1)20×10+20×10×2+10×10×2
=200+400+200
=800(平方厘米)
800平方厘米=8平方分米
答:做这个玻璃容器至少需要玻璃8平方分米。
(2)20×10×4=800(立方厘米)
答:这块石头的体积大约是800立方厘米。
【点睛】(1)关键是先弄清无盖长方体缺少哪个面,需要求哪几个面的面积,然后灵活运用长方体的表面积公式解答。
(2)本题考查不规则物体体积的求法,关键是将求石头的体积转移到求水下降部分的体积,根据长方体的体积公式列式计算。
6.2.71平方米
【分析】求做一只罩空调的长方体套子至少需要布的面积,就是求长方体的上面、前后面、左右面共5个面的面积之和;根据“长×宽+长×高×2+宽×高×2”,代入数据计算即可求解。
【详解】0.5×0.3+0.5×1.6×2+0.3×1.6×2
=0.15+1.6+0.96
=2.71(平方米)
答:做这只套子至少需要用2.71平方米的布。
【点睛】关键是先弄清罩空调的套子缺少下面,只需求其他五个面的面积之和,灵活运用长方体的表面积公式解答。
7.(1)236平方分米
(2)1560元
【分析】(1)求做这个油箱需要铁皮的面积,就是求这个长方体油箱的表面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答;
(2)根据长方体容积公式:容积=长×宽×高,代入数据,求出这个长方体油箱的容积,再乘6.5,即可求出加满这个油箱需要的钱数。
【详解】(1)(8×6+8×5+6×5)×2
=(48+40+30)×2
=(88+30)×2
=118×2
=236(平方分米)
答:做这个油箱至少需要236平方分米的铁皮。
(3)8×6×5
=48×5
=240(立方分米)
240立方分米=240升
240×6.5=1560(元)
答:加满这个油箱需1560元。
【点睛】熟练掌握长方体表面积公式,长方体容积公式是解答本题的关键,注意单位名数的换算。
8.(1)74平方分米
(2)6立方分米
【分析】(1)所需的玻璃面积就是长方体五个面的面积,即一个底面和四个侧面。计算公式为:长×宽+(长×高+宽×高)×2。
(2)鹅卵石的体积相当于上升的水的体积,水的体积是长为5分米,宽为4分米,高为0.3分米的长方体体积,长方体体积=长×宽×高。
【详解】(1)5×4+(4×3+5×3)×2
=20+(12+15)×2
=20+27×2
=20+54
=74(平方分米)
答:做这个鱼缸至少需要玻璃74平方分米。
(2)5×4×0.3=6(立方分米)
答:鹅卵石的体积一共是6立方分米。
【点睛】本题主要考查长方体的表面积公式和体积公式以及不规则物体的体积求法。
9.(1)775平方厘米;(2)375平方厘米;(3)1875立方厘米;(4)不是;见详解
【分析】(1)当x=5时,焊接无盖盒子所用的铁皮面积等于一个长为35厘米,宽为25厘米的长方形面积减去4个边长为5厘米的正方形的面积,利用长方形和正方形的面积公式即可得解。
(2)当x=5时,这个盒子的占地面积是一个长为(35-2×5)厘米,宽为(25-2×5)厘米的长方形,利用长方形的面积公式即可得解。
(3)根据长方体的容积公式:V=Sh,代入数据即可求出这个盒子的容积。
(4)可假设x=1和x=2时,先分别求出长方体的长、宽、高,再利用长方体的容积公式,分别求出这两种情况下长方体的容积,再与x=5时所求的长方体盒子的容积比较大小,即可得解。
【详解】(1)当x=5时,焊接无盖盒子所用的面积为:
S=35×25-4×52
=875-4×25
=875-100
=775 (平方厘米)
答:焊接无盖盒子用了775平方厘米的铁皮。
(2)当x =5时,这个盒子占地为长方形,
该长方形的长为:
35-2x
=35-2×5
=35-10
=25(厘米)
该长方形的长为:
25-2x
=25-2×5
=25-10
=15(厘米)
25×15=375(平方厘米)
答:这个盒子的占地面积是375平方厘米。
(3)当x=5时,这个盒子的容积为占地面积乘盒高。
375×5=1875(立方厘米)
答:这个盒子的容积是1875立方厘米。
(4)x可取的数值很多,在这些数值中,x=5时的盒子容积不是最小的。
理由如下:
当x=1时,
V=(35-2)×(25-2)×1
=33×23×1
=759(立方厘米)
当x=2时,
V=(35-4)×(25-4)×2
=31×21×2
=1302(立方厘米)
759立方厘米<1875立方厘米,1302立方厘米<1875立方厘米
答:在这些数值中,x=5时的盒子容积不是最小的。
【点睛】此题主要考查长方体的特征、长方体的表面积以及长方体的容积的计算方法。
10.68平方分米
【分析】根据长方体的棱长总和=(长+宽+高)×4,因为长方体的底面是正方形,所以用棱长总和减去4条高的长度再除以8就是长方体底面边长,糊纸的面积是4个侧面和一个底面的面积,所以无盖的长方体面积=1个底面的面积+4个侧面的面积,代入数据解答即可。
【详解】(48-8×4)÷8
=(48-32)÷8
=16÷8
=2(分米)
2×2+2×8×4
=4+64
=68(平方分米)
答:至少需要68平方分米的纸。
【点睛】此题主要考查长方体的棱长总和公式、表面积公式的灵活运用,关键是熟记公式。
11.2664平方厘米;会
【分析】3分米=30厘米,水接触玻璃的面积相当于无盖的长方体表面积,无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,代入数据即可求出水接触玻璃的面积;先根据长方体的体积=长×宽×高,代入数据求出玻璃缸的体积以及水的体积,然后根据正方体的体积=棱长×棱长×棱长,代入数据求出铁块的体积,最后把水和铁块的体积相加,结果和玻璃缸的体积比较即可。
【详解】3分米=30厘米
24×30+24×18×2+30×18×2
=720+864+1080
=2664(平方厘米)
玻璃缸的体积:30×24×22=15840(立方厘米)
水的体积:30×24×18=12960(立方厘米)
铁块体积:15×15×15=3375(立方厘米)
12960+3375=16335(立方厘米)
16335>12960
答:水接触玻璃的面积是2664平方厘米;水会溢出来。
【点睛】本题主要考查了长方体表面积公式、长方体体积公式、正方体体积公式的灵活应用,要熟练掌握相关公式。
12.(1)48平方米;(2)80平方米
【分析】(1)根据占地面积=长×宽,用16×0.3求出每个台阶的占地面积,再乘10即可求出10个台阶的占地面积;
(2)通过平移可知,台阶的贴地砖的面积相当于10个台阶的前面和上面的面积和,据此列式(16×0.3+16×0.2)×10解答。
【详解】(1)16×0.3×10=48(平方米)
答:10级这样的台阶共占地48平方米。
(2)(16×0.3+16×0.2)×10
=(4.8+3.2)×10
=8×10
=80(平方米)
答:给这些台阶贴上地砖,至少需要80平方米的地砖。
【点睛】本题主要考查了长方体表面积公式的灵活应用,明确求哪些面的面积是解答本题的关键。
13.(1)48平方米;(2)104平方米;(3)96吨
【分析】(1)根据长方体的底面积=长×宽,用8×6即可求出蓄水池的占地面积;
(2)无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,用8×6+8×2×2+6×2×2即可求出抹水泥部分的面积;
(3)根据长方体的体积=长×宽×高,用8×6×2即可求出水池的容积,再用乘法求出水池最多能蓄水多少吨。
【详解】(1)8×6=48(平方米)
答:这个蓄水池的占地面积是48平方米。
(2)8×6+8×2×2+6×2×2
=48+32+24
=104(平方米)
答:抹水泥部分的面积是104平方米。
(3)8×6×2=96(立方米)
96×1=96(吨)
答:这个水池最多能蓄水96吨。
【点睛】本题主要考查了长方体的表面积公式、体积公式的灵活应用,要熟练掌握相关公式。
14.将12×10这个面重合摞在一起,拼成一个长12厘米、宽10厘米、高24厘米的长方体最节约包装纸;1296平方厘米
【分析】求最少要用包装纸多少平方厘米,把这3个长方体盒子的最大面,即12×10这个面重合摞在一起,拼成一个长12厘米、宽10厘米、高4×6厘米的长方体最节约包装纸,根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出这个长方体的表面积即可。
【详解】将12×10这个面重合摞在一起
6×4=24(厘米)
(12×10+12×24+24×10)×2
=(120+288+240)×2
=(408+240)×2
=648×2
=1296(平方厘米)
答:将12×10这个面重合摞在一起最节省包装纸,至少需要包装纸1296平方厘米。
【点睛】本题关键是要找出拼组后的长方体的长宽高各是多少,然后根据长方体表面积公式求解。
15.(1)456平方分米;(2)192立方分米
【分析】(1)玻璃鱼缸是无盖的,少一个上底面,实际上是求长方体4个侧面和1个底面的面积之和,根据长方体的表面积公式:S=a×b+a×h×2+b×h×2,代入数据即可求出做这个玻璃鱼缸至少需要多少平方分米的玻璃。
(2)石头完全浸没在水里后,石头的体积=水面上升的体积,水面上升的体积可看作长为12分米,宽为8分米,高为(7-5)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【详解】(1)
=
=456(平方分米)
(2)12×8×(7-5)
=96×2
=192(立方分米)
答:这块石头的体积是192立方分米。
【点睛】此题主要考查长方体的表面积和体积的计算方法,掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用公式,解决问题。
16.(1)10;7;6;(2)右面的面积是42平方厘米,上面的面积是70平方厘米,前面的面积是60平方厘米
【分析】(1)根据题意可知,这个长方体的长是10厘米,宽是7厘米,高是(16-10)厘米;
(2)根据长方形的面积公式,用7×(16-10)即可求出右面的面积;用10×7即可求出上面的面积;用10×(16-10)即可求出前面的面积。
【详解】(1)16-10=6(厘米)
这个长方体的长是10厘米,宽是7厘米,高是6厘米;
(2)右面:7×6=42(平方厘米)
上面:10×7=70(平方厘米)
前面:10×6=60(平方厘米)
答:右面的面积是42平方厘米,上面的面积是70平方厘米,前面的面积是60平方厘米。
【点睛】本题主要考查了长方体的认识以及长方体表面的面积求解。
17.(1)72立方分米
(2)68平方分米
(3)2分米
【分析】(1)长方体的体积=长×宽×高,将长方体容器长宽高的数据带入公式计算即可;
(2)水与容器的接触面积是高度为4分米的长方体四个侧面的面积和一个底面的面积,
侧面面积=两个前面的面积+两个左面的面积,前面的面积=水高×长,
左面的面积=水高×宽,底面的面积=长×宽,代入数据计算即可;
(3)水的体积前后没变,所以先求水的体积,用水的体积除以前面的面积就等于水面的高度。
【详解】(1)
=
=(立方分米)
答:这个长方体容器的容积是72立方分米。
(2)
=32+36
=68(平方分米)
答:水与容器的接触面积是68平方分米。
(3)
=48÷24
=2(分米)
答:如果以这个长方体的前面为底面把长方体容器倒放在桌面上,这时水深是2分米。
【点睛】主要考查了长方体的体积以及表面积的相关知识,重点是要熟记长方体体积的计算公式。
18.(1)52平方厘米;
(2)24立方厘米
【分析】(1)由图可知,长方体的长为(8-2×2)厘米,长方体的宽为3厘米,长方体的高为2厘米,利用“长方体的表面积=(长×宽+宽×高+长×高)×2”求出这个长方体的表面积;
(2)已知长方体的长、宽、高,利用“长方体的体积=长×宽×高”求出这个长方体的体积,据此解答。
【详解】(1)8-2×2
=8-4
=4(厘米)
(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(平方厘米)
答:这个长方体的表面积是52平方厘米。
(2)4×3×2=24(立方厘米)
答:折成长方体后它的体积是24立方厘米。
【点睛】根据长方体的展开图确定长方体的长、宽、高,并掌握长方体的表面积和体积的计算公式是解答题目的关键。
19.96平方厘米
【分析】根据题意可知,木块平均分成两块,表面积增加了2个长方形面,长方形的长为8厘米,宽为6厘米,根据长方形的面积公式,用6×8×2即可求出增加的表面积。
【详解】6×8×2=96(平方厘米)
答:两块木块的表面积的和比原来木块的表面积增加了96平方厘米。
【点睛】本题主要考查了立体图形的切拼,注意表面积增加了哪些面。
20.672平方厘米;640立方厘米
【分析】如图所示,原来长方体的高增加5厘米后,表面积增加上面小长方体4个侧面的面积,长方体的底面是正方形时,其它4个侧面是形状完全相同的长方形,根据增加的表面积表示出上面小长方体一个侧面的面积,再求出底面正方形的边长,最后利用“长方体的表面积=(长×宽+宽×高+长×高)×2”“长方体的体积=长×宽×高”求出原来长方体的表面积和体积,据此解答。
【详解】
80÷4÷5
=20÷5
=4(厘米)
表面积:(4×4+4×40+4×40)×2
=(16+160+160)×2
=336×2
=672(平方厘米)
体积:4×4×40
=16×40
=640(立方厘米)
答:原来长方体的表面积是672平方厘米,体积是640立方厘米。
【点睛】根据增加的表面积求出原来长方体的长和宽,并掌握长方体的表面积和体积的计算公式是解答题目的关键。
21.360立方厘米
【分析】将高减少4厘米,表面积减少的部分是一个高度为4的长方体的侧面积,用96÷4求出底面周长,因为底面是正方形,底面周长÷4即可求出正方形的边长,原来长方体的高就是边长加上4,长方体的体积=长×宽×高,代入数据计算即可。
【详解】96÷4=24(厘米)
24÷4=6(厘米)
6+4=10(厘米)
6×6×10
=36×10
=360(立方厘米)
答:原来长方体的体积是360立方厘米。
【点睛】此题考查长方体的体积的求法,明确减少部分的面积是长方体的侧面积是解题的关键,注意长方体的侧面积=底面周长×高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
长方体和正方体专项突破-数学五年级下册人教版
1.一个表面积是96平方厘米的正方体,把它截成5个完全相同的长方体后,表面积增加了多少平方厘米?
2.一个房间长6米,宽3.5米,高3米,门窗面积8平方米,现在要把这个房间的四壁和顶面粉刷水泥,如果每平方米用涂料0.25千克,一共需要涂料多少千克?
3.一种长方体通风管,长2米,宽和高都是10厘米,做30节这样的通风管至少需要铁皮多少平方分米?
4.一个游泳池,长是40米,宽是25米,深是2.2米。
(1)这个游泳池的占地面积是多少?
(2)建造这个游泳池需挖土多少?
(3)要在它的四壁和底面铺上瓷砖,铺瓷砖的面积是多少?
5.一个无盖长方体玻璃容器的长是20厘米,宽和高都是10厘米。
(1)做这个玻璃容器至少需要玻璃多少平方分米?(玻璃厚度忽略不计)
(2)在这个长方体容器中加入一些水,来测量石头的体积,具体过程如图所示,这块石头的体积大约是多少立方厘米?
6.夏大妈家的柜式空调长0.5米,宽0.3米,高1.6米,为了防灰尘,夏大妈准备用布做一只长方体套子把空调罩起来,请你帮她算下,做这只套子至少需要用多少平方米的布?(接头处忽略不计)
7.一个长方体油箱,长8分米,宽6分米,高5分米。
(1)做这个油箱至少需要多少平方分米的铁皮?
(2)如果每升油6.5元,加满这个油箱需多少元?
8.一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(1)做这个鱼缸至少需要玻璃多少平方分米?
(2)鱼缸里有一些水,往水里放入一些鹅卵石,水面上升了0.3分米,鹅卵石的体积一共是多少立方分米?
9.一块长方形铁皮,如图,从四个角各切掉一个边长为x厘米的正方形,焊接成一个无盖盒子。
(1)当x=5时,焊接无盖盒子用了多少铁皮?
(2)当x=5时,这个盒子的占地面积是多少?
(3)当x=5时,这个盒子的容积是多少?
(4)x可取的数值很多,在这些数值中,x=5时的盒子容积是最小的吗?请回答并写出过程。
10.用一根长48分米的铁丝做一个长方体的框架,使它的高为8分米,底面是一个正方形(如图),再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸?
11.在一个长3分米,宽24厘米,高22厘米的玻璃缸中,水深18厘米,水接触玻璃的面积有多大?将一个棱长15厘米的正方体铁块放入水中后,缸中的水会溢出来吗?(通过计算来说明)
12.剧院大门前有10级台阶,每级台阶长16米,宽0.3米,高0.2米。
(1)10级这样的台阶共占地多少平方米?
(2)给这些台阶贴上地砖,至少需要多少平方米的地砖?
13.挖一个长8米、宽6米、深2米的蓄水池。
(1)这个蓄水池的占地面积是多少平方米?
(2)如果给这个蓄水池的四周和底部抹上水泥,抹水泥部分的面积是多少平方米?
(3)这个水池最多能蓄水多少吨?(1立方米的水重1吨)
14.端午节,笑笑妈妈准备将自己做的4盒绿豆糕包装在一起送给邻居。每盒绿豆糕长为12厘米、宽为10厘米、高为6厘米。怎样包装最节省包装纸?至少需要包装纸多少平方厘米?(接口处不计)
15.一个无盖的玻璃鱼缸,长12分米,宽8分米,高9分米。
(1)做这个玻璃鱼缸至少需要多少平方分米的玻璃?
(2)这个鱼缸内原来水深5分米,把一块石头完全浸没水中,水面上升到7分米,这块石头的体积是多少?
16.亮亮用长方形纸板制作一个长方体,他先把一张长16厘米,宽7厘米的纸板沿着虚线对折,做出了长方体相邻的两个面(如下图),然后再用纸板做出其它4个面,围成长方体。
(1)这个长方体的长是( )厘米,宽是( )厘米,高是( )厘米。
(2)计算这个长方体的右面、上面、前面的面积各是多少平方厘米?
17.一个密封的长方体容器,从里面量长4dm,宽3dm,高6dm,水深4dm。
(1)这个长方体容器的容积是多少dm3?
(2)水与容器的接触面积是多少dm2?
(3)如果以这个长方体的前面为底面把长方体容器倒放在桌面上,这时水深是多少?
18.有一张长方体表面展开图(如图)。
(1)这个长方体的表面积是多少平方厘米?
(2)折成长方体后它的体积是多少立方厘米?
19.把下图的木块平均分成两块,两块木块的表面积的和比原来木块的表面积增加了多少平方厘米?
20.一个高40厘米,底面是正方形的长方体,如果高增加5厘米,表面积就增加80平方厘米,求原来长方体的表面积和体积各是多少?
21.—个底面是正方形的长方体,如果把高减少4cm,就变成了一个正方体。表面积相应减少96cm2,原来长方体的体积是多少?
参考答案:
1.128平方厘米
【分析】根据正方体的表面积=棱长×棱长×6,已知正方体的表面积可以求出一个面的面积,把这个正方体截成5个完全相同的长方体后,表面积增加了(2×4)个截面的面积,把数据代入公式解答。
【详解】96÷6×(2×4)
=16×8
=128(平方厘米)
答:表面积增加了128平方厘米。
2.17.5千克
【分析】根据长方体表面积的计算方法,首先分清求的是哪5个面的总面积,即上面、前后面、左右面;再减去门窗的面积,求出需要粉刷的面积;然后根据乘法的意义求出一共需要涂料的质量。
【详解】6×3.5+6×3×2+3.5×3×2-8
=21+36+21-8
=70(平方米)
70×0.25=17.5(千克)
答:一共需要涂料17.5千克。
3.2400平方分米
【分析】长方体通风管只有4个面,用长×宽×2+长×高×2,求出一个通风管的表面积,再乘30即可。
【详解】2米=20分米
10厘米=1分米
20×1×2+20×1×2
=40+40
=80(平方分米)
80×30=2400(平方分米)
答:做30节这样的通风管至少需要铁皮2400平方分米。
4.(1)1000平方米
(2)2200立方米
(3)1286平方米
【分析】(1)根据长方形的面积公式:S=ab,即用40乘25即可求出这个游泳池的占地面积;
(2)根据长方体的体积公式:V=abh,据此代入数值进行求出建造这个游泳池需挖土多少;
(3)要在它的四壁和底面铺上瓷砖,则瓷砖的面积等于长方体五个面的面积(除去上面),这五个面的面积=(长×高+宽×高)×2+长×宽,据此进行计算即可。
【详解】(1)40×25=1000(平方米)
答:这个游泳池的占地面积是1000平方米。
(2)40×25×2.2
=1000×2.2
=2200(立方米)
答:建造这个游泳池需挖土2200立方米。
(3)(40×2.2+25×2.2)×2+40×25
=(88+55)×2+1000
=143×2+1000
=286+1000
=1286(平方米)
答:铺瓷砖的面积是1286平方米。
【点睛】本题考查长方体的体积和表面积,熟记公式是解题的关键。
5.(1)8平方分米
(2)800立方厘米
【分析】(1)根据题意,已知无盖长方体玻璃容器的长、宽、高,求做这个玻璃容器至少需要玻璃的面积,就是求长方体的下面、前后面、左右面共5个面的面积;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,再根据进率“1平方分米=100平方厘米”换算单位即可。
(2)从图中可知,取出石头后水面下降4厘米,那么水下降部分的体积等于这块石头的体积;水下降部分是一个长20厘米、宽10厘米、高4厘米的长方体,根据长方体的体积=长×宽×高,代入数据计算,即可求出这块石头的体积。
【详解】(1)20×10+20×10×2+10×10×2
=200+400+200
=800(平方厘米)
800平方厘米=8平方分米
答:做这个玻璃容器至少需要玻璃8平方分米。
(2)20×10×4=800(立方厘米)
答:这块石头的体积大约是800立方厘米。
【点睛】(1)关键是先弄清无盖长方体缺少哪个面,需要求哪几个面的面积,然后灵活运用长方体的表面积公式解答。
(2)本题考查不规则物体体积的求法,关键是将求石头的体积转移到求水下降部分的体积,根据长方体的体积公式列式计算。
6.2.71平方米
【分析】求做一只罩空调的长方体套子至少需要布的面积,就是求长方体的上面、前后面、左右面共5个面的面积之和;根据“长×宽+长×高×2+宽×高×2”,代入数据计算即可求解。
【详解】0.5×0.3+0.5×1.6×2+0.3×1.6×2
=0.15+1.6+0.96
=2.71(平方米)
答:做这只套子至少需要用2.71平方米的布。
【点睛】关键是先弄清罩空调的套子缺少下面,只需求其他五个面的面积之和,灵活运用长方体的表面积公式解答。
7.(1)236平方分米
(2)1560元
【分析】(1)求做这个油箱需要铁皮的面积,就是求这个长方体油箱的表面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答;
(2)根据长方体容积公式:容积=长×宽×高,代入数据,求出这个长方体油箱的容积,再乘6.5,即可求出加满这个油箱需要的钱数。
【详解】(1)(8×6+8×5+6×5)×2
=(48+40+30)×2
=(88+30)×2
=118×2
=236(平方分米)
答:做这个油箱至少需要236平方分米的铁皮。
(3)8×6×5
=48×5
=240(立方分米)
240立方分米=240升
240×6.5=1560(元)
答:加满这个油箱需1560元。
【点睛】熟练掌握长方体表面积公式,长方体容积公式是解答本题的关键,注意单位名数的换算。
8.(1)74平方分米
(2)6立方分米
【分析】(1)所需的玻璃面积就是长方体五个面的面积,即一个底面和四个侧面。计算公式为:长×宽+(长×高+宽×高)×2。
(2)鹅卵石的体积相当于上升的水的体积,水的体积是长为5分米,宽为4分米,高为0.3分米的长方体体积,长方体体积=长×宽×高。
【详解】(1)5×4+(4×3+5×3)×2
=20+(12+15)×2
=20+27×2
=20+54
=74(平方分米)
答:做这个鱼缸至少需要玻璃74平方分米。
(2)5×4×0.3=6(立方分米)
答:鹅卵石的体积一共是6立方分米。
【点睛】本题主要考查长方体的表面积公式和体积公式以及不规则物体的体积求法。
9.(1)775平方厘米;(2)375平方厘米;(3)1875立方厘米;(4)不是;见详解
【分析】(1)当x=5时,焊接无盖盒子所用的铁皮面积等于一个长为35厘米,宽为25厘米的长方形面积减去4个边长为5厘米的正方形的面积,利用长方形和正方形的面积公式即可得解。
(2)当x=5时,这个盒子的占地面积是一个长为(35-2×5)厘米,宽为(25-2×5)厘米的长方形,利用长方形的面积公式即可得解。
(3)根据长方体的容积公式:V=Sh,代入数据即可求出这个盒子的容积。
(4)可假设x=1和x=2时,先分别求出长方体的长、宽、高,再利用长方体的容积公式,分别求出这两种情况下长方体的容积,再与x=5时所求的长方体盒子的容积比较大小,即可得解。
【详解】(1)当x=5时,焊接无盖盒子所用的面积为:
S=35×25-4×52
=875-4×25
=875-100
=775 (平方厘米)
答:焊接无盖盒子用了775平方厘米的铁皮。
(2)当x =5时,这个盒子占地为长方形,
该长方形的长为:
35-2x
=35-2×5
=35-10
=25(厘米)
该长方形的长为:
25-2x
=25-2×5
=25-10
=15(厘米)
25×15=375(平方厘米)
答:这个盒子的占地面积是375平方厘米。
(3)当x=5时,这个盒子的容积为占地面积乘盒高。
375×5=1875(立方厘米)
答:这个盒子的容积是1875立方厘米。
(4)x可取的数值很多,在这些数值中,x=5时的盒子容积不是最小的。
理由如下:
当x=1时,
V=(35-2)×(25-2)×1
=33×23×1
=759(立方厘米)
当x=2时,
V=(35-4)×(25-4)×2
=31×21×2
=1302(立方厘米)
759立方厘米<1875立方厘米,1302立方厘米<1875立方厘米
答:在这些数值中,x=5时的盒子容积不是最小的。
【点睛】此题主要考查长方体的特征、长方体的表面积以及长方体的容积的计算方法。
10.68平方分米
【分析】根据长方体的棱长总和=(长+宽+高)×4,因为长方体的底面是正方形,所以用棱长总和减去4条高的长度再除以8就是长方体底面边长,糊纸的面积是4个侧面和一个底面的面积,所以无盖的长方体面积=1个底面的面积+4个侧面的面积,代入数据解答即可。
【详解】(48-8×4)÷8
=(48-32)÷8
=16÷8
=2(分米)
2×2+2×8×4
=4+64
=68(平方分米)
答:至少需要68平方分米的纸。
【点睛】此题主要考查长方体的棱长总和公式、表面积公式的灵活运用,关键是熟记公式。
11.2664平方厘米;会
【分析】3分米=30厘米,水接触玻璃的面积相当于无盖的长方体表面积,无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,代入数据即可求出水接触玻璃的面积;先根据长方体的体积=长×宽×高,代入数据求出玻璃缸的体积以及水的体积,然后根据正方体的体积=棱长×棱长×棱长,代入数据求出铁块的体积,最后把水和铁块的体积相加,结果和玻璃缸的体积比较即可。
【详解】3分米=30厘米
24×30+24×18×2+30×18×2
=720+864+1080
=2664(平方厘米)
玻璃缸的体积:30×24×22=15840(立方厘米)
水的体积:30×24×18=12960(立方厘米)
铁块体积:15×15×15=3375(立方厘米)
12960+3375=16335(立方厘米)
16335>12960
答:水接触玻璃的面积是2664平方厘米;水会溢出来。
【点睛】本题主要考查了长方体表面积公式、长方体体积公式、正方体体积公式的灵活应用,要熟练掌握相关公式。
12.(1)48平方米;(2)80平方米
【分析】(1)根据占地面积=长×宽,用16×0.3求出每个台阶的占地面积,再乘10即可求出10个台阶的占地面积;
(2)通过平移可知,台阶的贴地砖的面积相当于10个台阶的前面和上面的面积和,据此列式(16×0.3+16×0.2)×10解答。
【详解】(1)16×0.3×10=48(平方米)
答:10级这样的台阶共占地48平方米。
(2)(16×0.3+16×0.2)×10
=(4.8+3.2)×10
=8×10
=80(平方米)
答:给这些台阶贴上地砖,至少需要80平方米的地砖。
【点睛】本题主要考查了长方体表面积公式的灵活应用,明确求哪些面的面积是解答本题的关键。
13.(1)48平方米;(2)104平方米;(3)96吨
【分析】(1)根据长方体的底面积=长×宽,用8×6即可求出蓄水池的占地面积;
(2)无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,用8×6+8×2×2+6×2×2即可求出抹水泥部分的面积;
(3)根据长方体的体积=长×宽×高,用8×6×2即可求出水池的容积,再用乘法求出水池最多能蓄水多少吨。
【详解】(1)8×6=48(平方米)
答:这个蓄水池的占地面积是48平方米。
(2)8×6+8×2×2+6×2×2
=48+32+24
=104(平方米)
答:抹水泥部分的面积是104平方米。
(3)8×6×2=96(立方米)
96×1=96(吨)
答:这个水池最多能蓄水96吨。
【点睛】本题主要考查了长方体的表面积公式、体积公式的灵活应用,要熟练掌握相关公式。
14.将12×10这个面重合摞在一起,拼成一个长12厘米、宽10厘米、高24厘米的长方体最节约包装纸;1296平方厘米
【分析】求最少要用包装纸多少平方厘米,把这3个长方体盒子的最大面,即12×10这个面重合摞在一起,拼成一个长12厘米、宽10厘米、高4×6厘米的长方体最节约包装纸,根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出这个长方体的表面积即可。
【详解】将12×10这个面重合摞在一起
6×4=24(厘米)
(12×10+12×24+24×10)×2
=(120+288+240)×2
=(408+240)×2
=648×2
=1296(平方厘米)
答:将12×10这个面重合摞在一起最节省包装纸,至少需要包装纸1296平方厘米。
【点睛】本题关键是要找出拼组后的长方体的长宽高各是多少,然后根据长方体表面积公式求解。
15.(1)456平方分米;(2)192立方分米
【分析】(1)玻璃鱼缸是无盖的,少一个上底面,实际上是求长方体4个侧面和1个底面的面积之和,根据长方体的表面积公式:S=a×b+a×h×2+b×h×2,代入数据即可求出做这个玻璃鱼缸至少需要多少平方分米的玻璃。
(2)石头完全浸没在水里后,石头的体积=水面上升的体积,水面上升的体积可看作长为12分米,宽为8分米,高为(7-5)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【详解】(1)
=
=456(平方分米)
(2)12×8×(7-5)
=96×2
=192(立方分米)
答:这块石头的体积是192立方分米。
【点睛】此题主要考查长方体的表面积和体积的计算方法,掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用公式,解决问题。
16.(1)10;7;6;(2)右面的面积是42平方厘米,上面的面积是70平方厘米,前面的面积是60平方厘米
【分析】(1)根据题意可知,这个长方体的长是10厘米,宽是7厘米,高是(16-10)厘米;
(2)根据长方形的面积公式,用7×(16-10)即可求出右面的面积;用10×7即可求出上面的面积;用10×(16-10)即可求出前面的面积。
【详解】(1)16-10=6(厘米)
这个长方体的长是10厘米,宽是7厘米,高是6厘米;
(2)右面:7×6=42(平方厘米)
上面:10×7=70(平方厘米)
前面:10×6=60(平方厘米)
答:右面的面积是42平方厘米,上面的面积是70平方厘米,前面的面积是60平方厘米。
【点睛】本题主要考查了长方体的认识以及长方体表面的面积求解。
17.(1)72立方分米
(2)68平方分米
(3)2分米
【分析】(1)长方体的体积=长×宽×高,将长方体容器长宽高的数据带入公式计算即可;
(2)水与容器的接触面积是高度为4分米的长方体四个侧面的面积和一个底面的面积,
侧面面积=两个前面的面积+两个左面的面积,前面的面积=水高×长,
左面的面积=水高×宽,底面的面积=长×宽,代入数据计算即可;
(3)水的体积前后没变,所以先求水的体积,用水的体积除以前面的面积就等于水面的高度。
【详解】(1)
=
=(立方分米)
答:这个长方体容器的容积是72立方分米。
(2)
=32+36
=68(平方分米)
答:水与容器的接触面积是68平方分米。
(3)
=48÷24
=2(分米)
答:如果以这个长方体的前面为底面把长方体容器倒放在桌面上,这时水深是2分米。
【点睛】主要考查了长方体的体积以及表面积的相关知识,重点是要熟记长方体体积的计算公式。
18.(1)52平方厘米;
(2)24立方厘米
【分析】(1)由图可知,长方体的长为(8-2×2)厘米,长方体的宽为3厘米,长方体的高为2厘米,利用“长方体的表面积=(长×宽+宽×高+长×高)×2”求出这个长方体的表面积;
(2)已知长方体的长、宽、高,利用“长方体的体积=长×宽×高”求出这个长方体的体积,据此解答。
【详解】(1)8-2×2
=8-4
=4(厘米)
(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(平方厘米)
答:这个长方体的表面积是52平方厘米。
(2)4×3×2=24(立方厘米)
答:折成长方体后它的体积是24立方厘米。
【点睛】根据长方体的展开图确定长方体的长、宽、高,并掌握长方体的表面积和体积的计算公式是解答题目的关键。
19.96平方厘米
【分析】根据题意可知,木块平均分成两块,表面积增加了2个长方形面,长方形的长为8厘米,宽为6厘米,根据长方形的面积公式,用6×8×2即可求出增加的表面积。
【详解】6×8×2=96(平方厘米)
答:两块木块的表面积的和比原来木块的表面积增加了96平方厘米。
【点睛】本题主要考查了立体图形的切拼,注意表面积增加了哪些面。
20.672平方厘米;640立方厘米
【分析】如图所示,原来长方体的高增加5厘米后,表面积增加上面小长方体4个侧面的面积,长方体的底面是正方形时,其它4个侧面是形状完全相同的长方形,根据增加的表面积表示出上面小长方体一个侧面的面积,再求出底面正方形的边长,最后利用“长方体的表面积=(长×宽+宽×高+长×高)×2”“长方体的体积=长×宽×高”求出原来长方体的表面积和体积,据此解答。
【详解】
80÷4÷5
=20÷5
=4(厘米)
表面积:(4×4+4×40+4×40)×2
=(16+160+160)×2
=336×2
=672(平方厘米)
体积:4×4×40
=16×40
=640(立方厘米)
答:原来长方体的表面积是672平方厘米,体积是640立方厘米。
【点睛】根据增加的表面积求出原来长方体的长和宽,并掌握长方体的表面积和体积的计算公式是解答题目的关键。
21.360立方厘米
【分析】将高减少4厘米,表面积减少的部分是一个高度为4的长方体的侧面积,用96÷4求出底面周长,因为底面是正方形,底面周长÷4即可求出正方形的边长,原来长方体的高就是边长加上4,长方体的体积=长×宽×高,代入数据计算即可。
【详解】96÷4=24(厘米)
24÷4=6(厘米)
6+4=10(厘米)
6×6×10
=36×10
=360(立方厘米)
答:原来长方体的体积是360立方厘米。
【点睛】此题考查长方体的体积的求法,明确减少部分的面积是长方体的侧面积是解题的关键,注意长方体的侧面积=底面周长×高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
