浙江省富阳市场口中学2014-2015学年高二5月检测数学(文)试题
文档属性
| 名称 | 浙江省富阳市场口中学2014-2015学年高二5月检测数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 114.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-26 00:00:00 | ||
图片预览


文档简介
场口中学5月检测
高二文科数学试题
命题人:孙金千 复核人:施海英
一、选择题:本大题共8小题,每小题3分,共24分。在每小题给出的四个选项中,只有一项符合题目要求。
1.下列函数中既是奇函数又是增函数的是( )
A. B. C. D.
2、设a∈R,则“a=-”是“直线l1: ax+2y-1=0与直线l2: x+(a+1)y+4=0垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.若实数满足不等式组,则的最小值等于( )
A. B. C. D.
4、设l是直线,α,β是两个不同的平面( )
A.若l∥α,l∥β,则α∥β B.若l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β D.若α⊥β,l∥α,则l⊥β
5.若角α的终边上有一点P(-1,m),且sinα=,则m的值为
A、 B、 C、或 D、
6.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于
A.10 cm3 B.20 cm3 C.30 cm3 D.40 cm3
7.已知双曲线的渐近线与圆相交,
则该双曲线的离心率的取值范围是( )
A. B. C. D.
8.已知,则方程f[f(x)]=1的根的个数是( )
A.3个 B.4个 C.5个 D.6个
二、填空题:本大题共7小题,9-12题:每小题6分,13-15题:每小题4分,共36分.
9.集合,若,则 ; ; .
10. 已知命题p:,x-1>lnx.命题q:,,
则p: ,(填命题),命题p∧(q)是 命题(填真或假)。
11.设等差数列的前项和为,若,则数列的公差 ; .
12、若函数,则 ,使的a的取值范围是 .
13.在直角三角形中,,,,若,
则 .
14.若实数满足,则的最小值是 .
15.已知椭圆的左右顶点为,点是椭圆上异于的点,若直线的斜率之积为,则椭圆的离心率是 .
三、解答题:本大题共4小题,共40分,解答应写出文字说明、证明过程或演算步骤。
16.(本题满分8分)已知的周长为,且
(1)求边长的值 (2)若,求的值
17.(本题满分8分)已知数列是首项为的等差数列,其前项和
满足.
(Ⅰ)求数列的通项公式;
(Ⅱ)设数列的前项和为,求的取值范围.
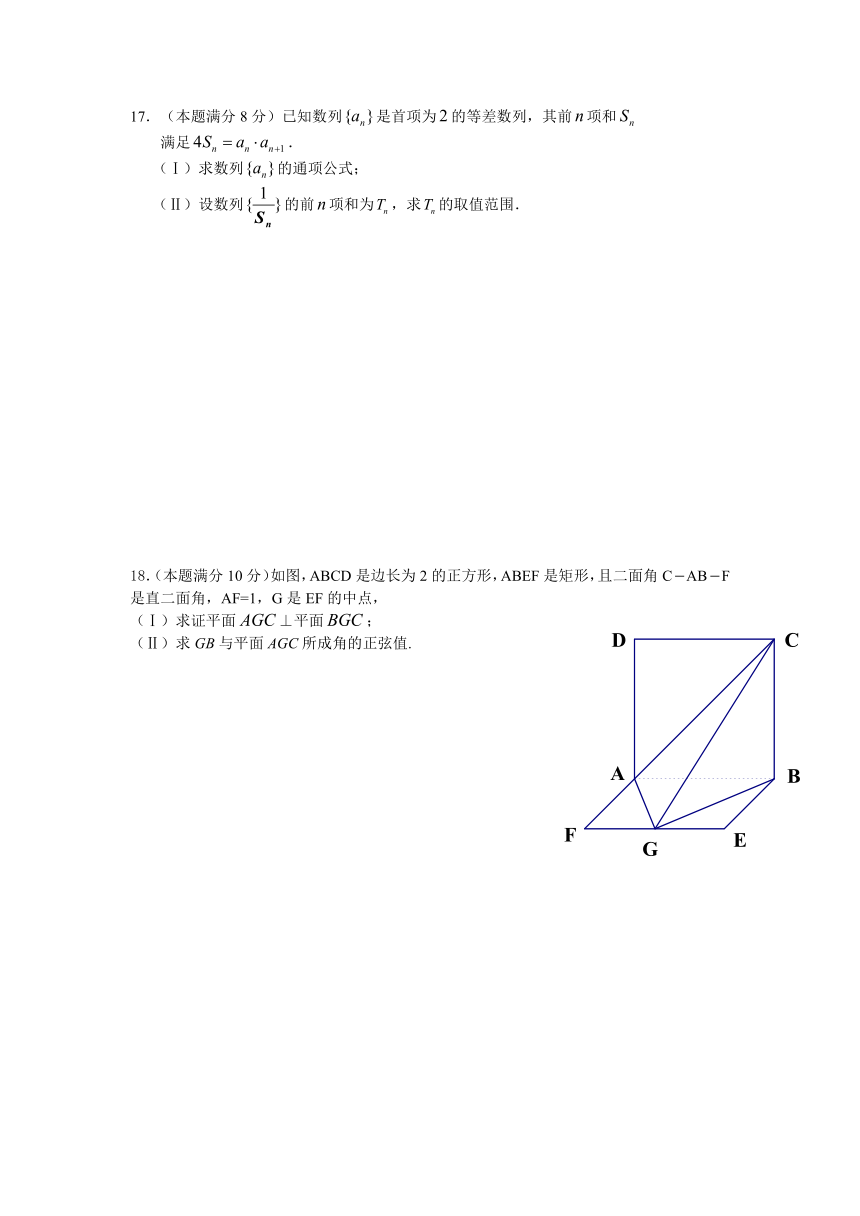
18.(本题满分10分)如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角CABF
是直二面角,AF=1,G是EF的中点,
(Ⅰ)求证平面⊥平面;
(Ⅱ)求GB与平面AGC所成角的正弦值.
19、(本题满分14分)已知函数f(x)=x2+(x-1)|x-a|.
(Ⅰ)若a=-1,解方程f(x)=1;
(Ⅱ)若函数f(x)在R上单调递增,求实数a的取值范围;
(Ⅲ)若函数f(x)在[2,3]上的最小值为6,求实数a的值.
高二文科数学试题答案
一、选择题:本大题共8小题,每小题3分,共24分。
BCDB ABAD
二、填空题:本大题共7小题,9-12题:每小题6分,13-15题:每小题4分,共36分.
9. {0,1},{1,0,-1},{-1} 10. (x(R,x-1≤lnx,真命题 11.
12、3 13. 14. -2 15.
三、解答题:本大题共4小题,共40分,解答应写出文字说明、证明过程或演算步骤。
16.(本题8分)已知的周长为,且
(1)求边长的值 (2)若,求的值
(1)sinB+sinC=sinA及正弦定理得b+c=a …………2分
又a+b+c=得a=4 …………4分
(2)S(ABC==3sinA
所以bc=6,b+c=4 …………6分
…………8分
17.已知数列是首项为的等差数列,其前项和满足.
(Ⅰ)求数列,的通项公式;
(Ⅱ)设数列的前项和为,求的取值范围.
17.解:(Ⅰ)设等差数列的公差为,由题意得,?,解得,
∴ …………………………………………………………………3分
(Ⅱ)由(Ⅰ)知……………5分
∴ 7分
8分
18.( 10分)如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角CABF
是直二面角,AF=1,G是EF的中点,
(Ⅰ)求证平面⊥平面;
(Ⅱ)求GB与平面AGC所成角的正弦值.
18、解法一:(几何法)(Ⅰ)证明:正方形ABCD 1分
∵二面角CABF是直二面角,CB⊥AB,∴CB⊥面ABEF 2分
∵AG,GB面ABEF,∴CB⊥AG, 又AD=2,AF= 1,ABEF是矩形,
G是EF的中点,∴AG=BG=,AB=2, AB2=AG2+BG2,
∴AG⊥BG 3分
∵CG∩BG=B ∴AG⊥平面CBG 4分
而AG面AGC, 故平面AGC⊥平面BGC 5分
(Ⅱ)解:如图,由(Ⅰ)知面AGC⊥面BGC,且交于GC,
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,7分
∴∠BGH是GB与平面AGC所成的角 8分
∴在Rt△CBG中
9分
又BG=,∴ 10分
解法二:(向量法)如图,以A为原点建立直角坐标系,则
A(0,0,0),B(0,2,0),C(0,2,2 ),G(1,1,0),
F(1,0,0).2分
(I)证明:,,,
∴,
∴AG⊥BG,AG⊥BC,而BG与BC是平面BCG内两相交直线,
∴AG⊥平面BCG,5分
又AG平面ACG,故平面ACG⊥平面BCG 6分
(II)由题意可得,,,7分
设平面AGC的法向量为,
由 9分
10分
20、(14分)已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1; (4分)
(2)若函数f(x)在R上单调递增,求实数a的取值范围;(4分)
(3)若函数f(x)在[2,3]上的最小值为6,求实数a的值.(6分)
20、(12分)解:(当a=-1时,f(x)=x2+(x-1)|x+1|,
故有,f(x)=, 1分
当x≥-1时,由f(x)=1,有2x2-1=1,解得x=1,或x=-1. 2分
当x<-1时,f(x)=1恒成立, 3分 ∴方程的解集为{x|x≤-1或x=1}. 4分
(2)f(x)=x2+(x﹣1)?|x﹣a|=, 5分
则若使函数f(x)在R上单调递增,
则, 7分
则; 8分
(3)若a≥3,则f(x)=(a+1)x﹣a在[2,3]上单调递增],
则函数f(x)在[2,3]上的最小值为6,可化为
fmin(x)=f(2)=2(a+1)﹣a=6,则a=4; 9分
若1≤a<3,则f(x)在[2,3]上单调递增,
则fmin(x)=f(2)=2(a+1)﹣a=6,则a=4无解, 11分
若a<1,<1,
则f(x)=x2+(x﹣1)?|x﹣a|在[2,3]上单调递增,
则fmin(x)=f(2)=2?22﹣(1+a)2+a=6,解得,a=0. 13分
综上所述,a=0或a=4. 14分
高二文科数学试题
命题人:孙金千 复核人:施海英
一、选择题:本大题共8小题,每小题3分,共24分。在每小题给出的四个选项中,只有一项符合题目要求。
1.下列函数中既是奇函数又是增函数的是( )
A. B. C. D.
2、设a∈R,则“a=-”是“直线l1: ax+2y-1=0与直线l2: x+(a+1)y+4=0垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.若实数满足不等式组,则的最小值等于( )
A. B. C. D.
4、设l是直线,α,β是两个不同的平面( )
A.若l∥α,l∥β,则α∥β B.若l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β D.若α⊥β,l∥α,则l⊥β
5.若角α的终边上有一点P(-1,m),且sinα=,则m的值为
A、 B、 C、或 D、
6.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于
A.10 cm3 B.20 cm3 C.30 cm3 D.40 cm3
7.已知双曲线的渐近线与圆相交,
则该双曲线的离心率的取值范围是( )
A. B. C. D.
8.已知,则方程f[f(x)]=1的根的个数是( )
A.3个 B.4个 C.5个 D.6个
二、填空题:本大题共7小题,9-12题:每小题6分,13-15题:每小题4分,共36分.
9.集合,若,则 ; ; .
10. 已知命题p:,x-1>lnx.命题q:,,
则p: ,(填命题),命题p∧(q)是 命题(填真或假)。
11.设等差数列的前项和为,若,则数列的公差 ; .
12、若函数,则 ,使的a的取值范围是 .
13.在直角三角形中,,,,若,
则 .
14.若实数满足,则的最小值是 .
15.已知椭圆的左右顶点为,点是椭圆上异于的点,若直线的斜率之积为,则椭圆的离心率是 .
三、解答题:本大题共4小题,共40分,解答应写出文字说明、证明过程或演算步骤。
16.(本题满分8分)已知的周长为,且
(1)求边长的值 (2)若,求的值
17.(本题满分8分)已知数列是首项为的等差数列,其前项和
满足.
(Ⅰ)求数列的通项公式;
(Ⅱ)设数列的前项和为,求的取值范围.
18.(本题满分10分)如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角CABF
是直二面角,AF=1,G是EF的中点,
(Ⅰ)求证平面⊥平面;
(Ⅱ)求GB与平面AGC所成角的正弦值.
19、(本题满分14分)已知函数f(x)=x2+(x-1)|x-a|.
(Ⅰ)若a=-1,解方程f(x)=1;
(Ⅱ)若函数f(x)在R上单调递增,求实数a的取值范围;
(Ⅲ)若函数f(x)在[2,3]上的最小值为6,求实数a的值.
高二文科数学试题答案
一、选择题:本大题共8小题,每小题3分,共24分。
BCDB ABAD
二、填空题:本大题共7小题,9-12题:每小题6分,13-15题:每小题4分,共36分.
9. {0,1},{1,0,-1},{-1} 10. (x(R,x-1≤lnx,真命题 11.
12、3 13. 14. -2 15.
三、解答题:本大题共4小题,共40分,解答应写出文字说明、证明过程或演算步骤。
16.(本题8分)已知的周长为,且
(1)求边长的值 (2)若,求的值
(1)sinB+sinC=sinA及正弦定理得b+c=a …………2分
又a+b+c=得a=4 …………4分
(2)S(ABC==3sinA
所以bc=6,b+c=4 …………6分
…………8分
17.已知数列是首项为的等差数列,其前项和满足.
(Ⅰ)求数列,的通项公式;
(Ⅱ)设数列的前项和为,求的取值范围.
17.解:(Ⅰ)设等差数列的公差为,由题意得,?,解得,
∴ …………………………………………………………………3分
(Ⅱ)由(Ⅰ)知……………5分
∴ 7分
8分
18.( 10分)如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角CABF
是直二面角,AF=1,G是EF的中点,
(Ⅰ)求证平面⊥平面;
(Ⅱ)求GB与平面AGC所成角的正弦值.
18、解法一:(几何法)(Ⅰ)证明:正方形ABCD 1分
∵二面角CABF是直二面角,CB⊥AB,∴CB⊥面ABEF 2分
∵AG,GB面ABEF,∴CB⊥AG, 又AD=2,AF= 1,ABEF是矩形,
G是EF的中点,∴AG=BG=,AB=2, AB2=AG2+BG2,
∴AG⊥BG 3分
∵CG∩BG=B ∴AG⊥平面CBG 4分
而AG面AGC, 故平面AGC⊥平面BGC 5分
(Ⅱ)解:如图,由(Ⅰ)知面AGC⊥面BGC,且交于GC,
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,7分
∴∠BGH是GB与平面AGC所成的角 8分
∴在Rt△CBG中
9分
又BG=,∴ 10分
解法二:(向量法)如图,以A为原点建立直角坐标系,则
A(0,0,0),B(0,2,0),C(0,2,2 ),G(1,1,0),
F(1,0,0).2分
(I)证明:,,,
∴,
∴AG⊥BG,AG⊥BC,而BG与BC是平面BCG内两相交直线,
∴AG⊥平面BCG,5分
又AG平面ACG,故平面ACG⊥平面BCG 6分
(II)由题意可得,,,7分
设平面AGC的法向量为,
由 9分
10分
20、(14分)已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1; (4分)
(2)若函数f(x)在R上单调递增,求实数a的取值范围;(4分)
(3)若函数f(x)在[2,3]上的最小值为6,求实数a的值.(6分)
20、(12分)解:(当a=-1时,f(x)=x2+(x-1)|x+1|,
故有,f(x)=, 1分
当x≥-1时,由f(x)=1,有2x2-1=1,解得x=1,或x=-1. 2分
当x<-1时,f(x)=1恒成立, 3分 ∴方程的解集为{x|x≤-1或x=1}. 4分
(2)f(x)=x2+(x﹣1)?|x﹣a|=, 5分
则若使函数f(x)在R上单调递增,
则, 7分
则; 8分
(3)若a≥3,则f(x)=(a+1)x﹣a在[2,3]上单调递增],
则函数f(x)在[2,3]上的最小值为6,可化为
fmin(x)=f(2)=2(a+1)﹣a=6,则a=4; 9分
若1≤a<3,则f(x)在[2,3]上单调递增,
则fmin(x)=f(2)=2(a+1)﹣a=6,则a=4无解, 11分
若a<1,<1,
则f(x)=x2+(x﹣1)?|x﹣a|在[2,3]上单调递增,
则fmin(x)=f(2)=2?22﹣(1+a)2+a=6,解得,a=0. 13分
综上所述,a=0或a=4. 14分
同课章节目录
