4.4 光的干涉 课件(共43张PPT)
文档属性
| 名称 | 4.4 光的干涉 课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-19 16:18:58 | ||
图片预览








文档简介
(共43张PPT)
第四章 光及其应用
粤教版 选择性必修一
第四节 光的干涉
新课导入
这些彩色条纹或图样是怎样形成的?
肥皂泡看起来常常是彩色的
雨后公路积水,上面漂浮的油膜也经常显现出彩色条纹或图样
牛顿 微粒说
光的本性学说的发展史
惠更斯 波动说
干涉现象是波动独有的特征,如果光真的是一种波,就必然会观察到光的干涉现象
知识回顾
机械波的干涉
2、产生干涉的条件
1、解释干涉现象
3、重叠区内一质点振动是加强还是减弱,取决于什么?
水波的干涉
知识回顾
机械波的干涉
水波的干涉
两列频率相同,振动方向相同,相位差恒定的两列波叠加,使某些区域的振动始终加强(波峰与波峰、波谷与波谷叠加),某些区域的振动始终减弱(波峰与波谷叠加),并且振动加强和振动减弱的区域相互间隔这种现象叫做波的干涉,形成的图样叫做干涉图样。
干涉现象是波动独有的特征,如果光真的是一种波,就必然会观察到光的干涉现象
思考1:光要发生干涉现象需要满足什么条件?
思考2:有没有什么方法可以获得相干光—频率相同的光呢?
相干光源(频率和振动情况一致)
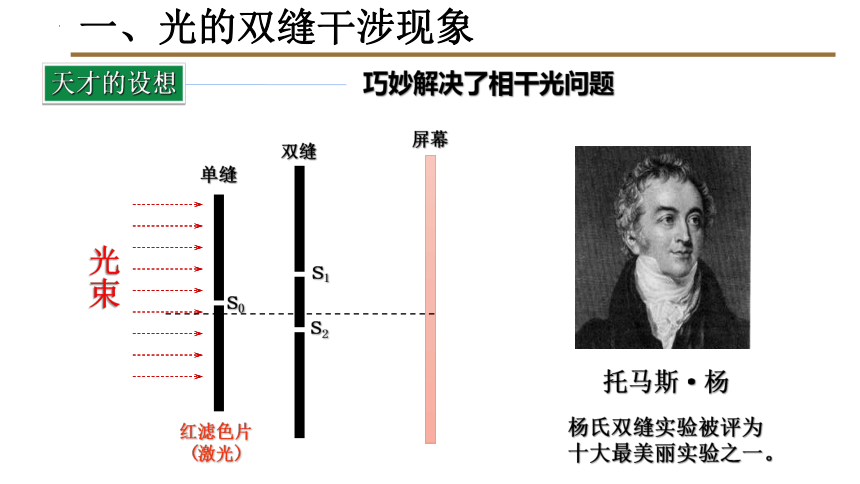
一、光的双缝干涉现象
一、光的双缝干涉现象
天才的设想
光束
单缝
双缝
红滤色片
(激光)
屏幕
s0
s1
s2
托马斯·杨
杨氏双缝实验被评为十大最美丽实验之一。
巧妙解决了相干光问题
一、光的双缝干涉现象
1、装置特点:
1)双缝到单缝的距离相等
2)双缝很近 d=0.1mm
2、单缝作用:
获得线光源,使光源有唯一的频率和振动情况.
3、双缝作用:
获得两个频率相同、振动情况完全相同的光源,叫相干光源
一、光的双缝干涉现象
单缝
双缝
S1
S
S2
屏
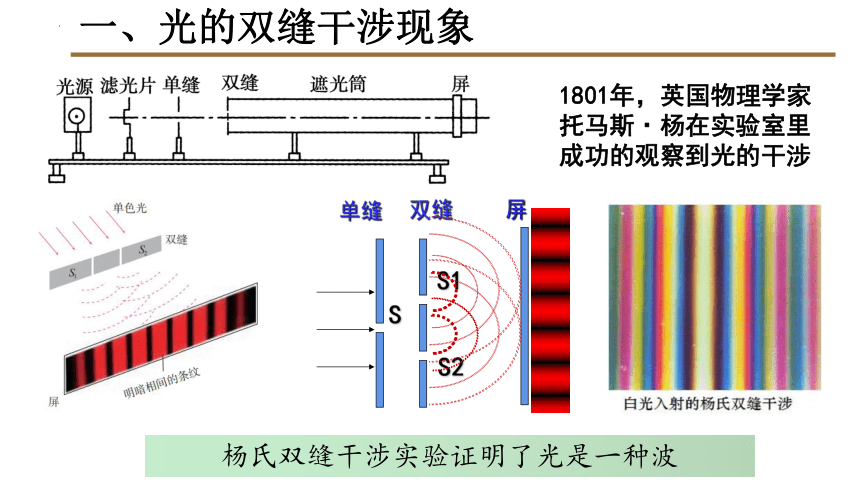
杨氏双缝干涉实验证明了光是一种波
1801年,英国物理学家托马斯·杨在实验室里成功的观察到光的干涉
一、光的双缝干涉现象
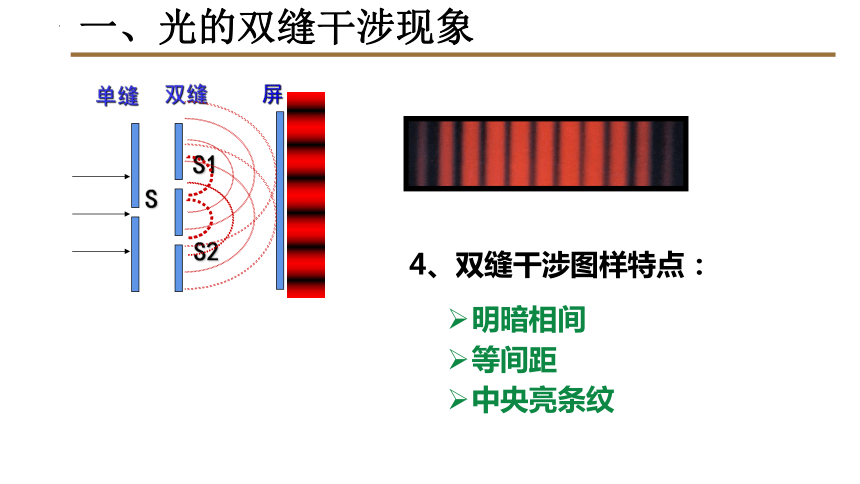
等间距
4、双缝干涉图样特点:
中央亮条纹
明暗相间
单缝
双缝
S1
S
S2
屏
二、对光的双缝干涉现象的解释
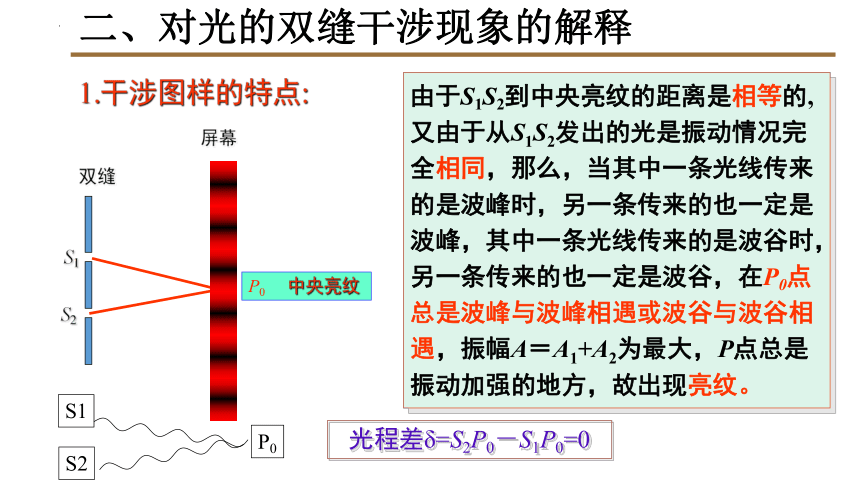
1.干涉图样的特点:
S1
S2
双缝
屏幕
P0 中央亮纹
由于S1S2到中央亮纹的距离是相等的, 又由于从S1S2发出的光是振动情况完全相同,那么,当其中一条光线传来的是波峰时,另一条传来的也一定是波峰,其中一条光线传来的是波谷时,另一条传来的也一定是波谷,在P0点总是波峰与波峰相遇或波谷与波谷相遇,振幅A=A1+A2为最大,P点总是振动加强的地方,故出现亮纹。
光程差δ=S2P0-S1P0=0
S1
S2
P0
二、对光的双缝干涉现象的解释
第一条亮纹的形成原因分析
光程差δ=S2P1-S1P1=λ
P1
第一亮纹
双缝
S1
S2
屏幕
S1
S2
P1
λ
λ
δ=λ
取P0点上方的点P1,若从S1S2发出的光到P1点的光程差,正好等于一个波长
δ = S2P1-S1P1=λ,则当其中一条光线传来的是波峰时,另一条传来的也一定是波峰,其中一条光传来的是波谷时,另一条传来的也一定是波谷,在P1点总是波峰与波峰相遇或波谷与波谷相遇,振幅A=A1+A2为最大,P1点总是振动加强的地方,故出现亮纹。
二、对光的双缝干涉现象的解释
P2
第二亮纹
2λ
第二条亮纹的形成原因分析
光程差δ=S2P2-S1P2=2λ
双缝
S1
S2
屏幕
二、对光的双缝干涉现象的解释
双缝
S1
S2
屏幕
P1 第一亮纹 δ=λ
P0 中央亮纹 δ=0
P2 第二亮纹 δ=2λ
P3 第三亮纹 δ=3λ
当光程差δ= k λ 时出现亮纹
以此类推
光程差 δ=S2Pk-S1Pk=kλ
P3 / 第三亮纹 δ= - 3λ
P2/ 第二亮纹 δ= - 2λ
P1/ 第一亮纹 δ= - λ
二、对光的双缝干涉现象的解释
当其中一条光传来的是波峰,另一条传来的就是波谷,其中一条光传来的是波谷,另一条传来的一定是波峰,Q1点总是波峰与波谷相遇,振幅最小,Q1点总是振动减弱的地方,故出现暗纹。
2.暗条纹形成的原因
取P0点上方的点Q1,与两个狭缝S1、S2光程差δ= S1Q1-S2Q1=λ/2
Q1
第一暗纹
双缝
S1
S2
屏幕
光程差 δ=S2Q1-S1Q1= /
二、对光的双缝干涉现象的解释
取P0点上方的点Q2,与两个狭缝S1、S2光程差δ= S1-S2=3λ/2
当其中一条光传来的是波峰,另一条传来的就是波谷,其中一条光线传来的是波谷,另一条传来的一定是波峰,Q2点总是波峰与波谷相遇,振幅最小,Q2点总是振动减弱的地方,故出现暗纹。
Q1
第一暗纹
双缝
S1
S2
屏幕
Q2
第二暗纹
光程差 δ=S2Q1-S1Q1=3 /
二、对光的双缝干涉现象的解释
双缝
S1
S2
屏幕
Q1 第一暗纹 δ=λ/2
Q2 第二暗纹 δ=3λ/2
Q3 / 第三暗纹 δ= - 5λ/2
Q3 第三暗纹 δ=5λ/2
Q2/ 第二暗纹 δ= - 3λ/2
Q1/ 第一暗纹 δ= - λ/2
当光程差δ=(2k+1)λ /2 ,即半波长奇数倍时,出现暗纹。
以此类推
光程差 δ=S2Qk-S1Qk=(2k+1)λ /2
二、对光的双缝干涉现象的解释
中央亮条纹
明暗相间
二、对光的双缝干涉现象的解释
(1)空间的某点距离光源S1和S2的光程差为0、λ、2λ、3λ等波长的整数倍(半波长的偶数倍)时,该点为振动加强点。
(2)空间的某点距离光源S1和S2的光程差为λ /2、3 λ/2、5λ/2等半波长的奇数倍时,该点为振动减弱点。
3.总结规律
光程差 δ= kλ
( k=0,±1,± 2,……)
光程差 δ =(2k+1)λ/2 ( k=0,±1, ± 2,……)
暗纹
产生明、暗条纹的条件
亮纹:光程差 δ = kλ( k= 0,±1, ± 2, ……)
暗纹:光程差 δ =(2k+1)λ/2 (k=0, ± 1, ± 2,……)
亮纹
空气真空
三、干涉条纹与光的波长之间的关系
双缝
S1
S2
屏幕
x
x
条纹间距的含义:
相邻两条亮条纹(或暗条纹)中心之间的距离叫作条纹间距.
影响因素:双缝到屏的距离、双缝间的距离、入射光的波长
光的双缝干涉实验中,条纹间距的含义是什么?它可能与哪些因素有关?
三、干涉条纹与光的波长之间的关系
θ
公式推导
d:双缝间距
l:挡板到屏的距离
单色光
波长:λ
挡板
屏
d:双缝间距
l:挡板到屏的距离
在线段P1S2上作P1M=P1 S1
由几何知识得
r2-r1=d sin θ ①
x=l tan θ≈l sin θ ②
消去 sin θ
r2-r1=d
d l
条纹间距的公式推导
亮条纹:d = k λ (k = 0,±1,±2 …)
亮条纹中心的位置为:x = kλ
相邻两个亮条纹或暗条纹的中心间距是:
x = λ
三、干涉条纹与光的波长之间的关系
1.由数学知识可得条纹间距公式为 ,其中l为双缝到屏的距离,d为双缝间的距离,λ为入射光的波长.
2.单色光的干涉图样:干涉条纹是等间距的明暗相间的条纹.
红光干涉条纹
蓝光干涉条纹
单色光
波长:λ
挡板
屏
d:双缝间距
l:挡板到屏的距离
三、干涉条纹与光的波长之间的关系
(1)对于同一干涉装置和同一单色光,条纹之间的距离相等.
(2)对于不同颜色的光,波长不同,由 x = λ知条纹之间的距离与光
波的波长成正比.对于同一装置,所用光源的波长越长,条纹之间的距离越大,即用红光时条纹之间的距离 ,用紫光时条纹之间的距离 .
红光干涉条纹
紫光干涉条纹
蓝光干涉条纹
最大
最小
对 x = λ 公式的理解
λ 增大
三、干涉条纹与光的波长之间的关系
如果用白光做双缝干涉实验,会得到怎样的干涉条纹?为什么?
(1)明暗相间的彩色条纹;
(2)中央为白色亮条纹;
(3)干涉条纹是以中央亮纹为对称点排列的;
(4)在每条彩色亮纹中红光总是在外侧,紫光在内侧。
条纹间距与光波的波长成正比
红光条纹间距最大,紫光条纹间距最小
课堂练习
1.如图所示,用频率为f的单色光(激光)垂直照射双缝,在光屏的P点出现第2条暗条纹,已知光速为c,则P到双缝S1、S2的距离之差|r1-r2|应为( )
B
课堂练习
2.如图是杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,P1为第一级亮纹的中心,若将双缝间的距离变小,其他条件不变,则( )
A.屏上干涉条纹的间距将变小
B.屏上O点仍然为中央亮条纹的中心
C.屏上P1位置仍然可能为亮条纹的中心
D.屏上P1位置可能为暗条纹的中心
BD
四、薄膜干涉
观察到灯焰的像出现了明暗相间的干涉条纹。该条纹是由液膜前后两个面反射的光相互叠加发生干涉形成的。
在酒精灯的灯芯上撒一些食盐,灯焰就能发出明亮的黄光。把铁丝圈在肥皂水中蘸一下,让它挂上一层薄薄的液膜。把这层液膜当作一个平面镜,用它观察灯焰的像。这个像与直接看到的灯焰有什么不同?请解析看到的现象。
四、薄膜干涉
四、薄膜干涉
2.现象解释
由于重力的作用,肥皂薄膜将形成上薄下厚的楔形。
光从薄膜的前后两个表面反射出来两列光波,这两列光波的频率相同,产生干涉。
前表面
后表面
四、薄膜干涉
光程差为波长的整数倍,形成亮条纹。
光程差为半波长的奇数倍,形成暗条纹。
白光照射时是彩色条纹
四、薄膜干涉
薄膜干涉的应用(一)——检查表面的平整程度
利用薄膜干涉检查平面的平整度:如图甲所示,在利用薄膜干涉检查平面的平整度时,在被检查平面与透明样板间垫一个薄片,使其间形成一个楔形的空气薄层。
样板下表面
工件上表面
空气薄膜
注:薄片厚度一般仅为零点零几毫米左右,只相当于一张纸片的厚度
四、薄膜干涉
薄膜干涉的应用(一)——检查表面的平整程度
当用单色光从上面照射时,入射光从空气层的上、下表面反射出两列光波,于是从反射光中看到干涉条纹。如果被测表面是平整的,得到的干涉图样必是一组 的直线;
如果观察到的干涉条纹不平行,则表示被检测表面微有凸起或凹下,这些凸起或凹下的地方的干涉条纹就弯曲。
平行
被测表面有凹下,亮条纹提前出现
被测表面有凸起,亮条纹延后出现
练习与应用
劈尖干涉是一种薄膜干涉,如图所示。将一块平板玻璃放置在另一平板玻璃之上,在一端夹入两张纸片,从而在两玻璃表面之间形成一个劈形空气薄膜,当光从上方入射后,从上往下看到的干涉条纹有如下特点:
(1)任意一条明条纹或暗条纹所在位置下面的薄膜厚度相等;
(2)任意相邻明条纹或暗条纹所对应的薄膜厚度差恒定。
现若在如图所示装置中抽去一张纸片,则当光入射到劈形空气薄膜后,从上往下可以观察到干涉条纹发生了怎样的变化?
3 面
4 面
1 面
2 面
d1
d2
l
θ
θ
两处光程差为 1=2d1, 2=2d2
2- 1= ,所以d2-d1= /2
由几何关系可得
即
结论:
当抽去一张纸片时,θ减小, l增大,即条纹变稀疏。
亮纹1
亮纹2
3 面
4 面
1 面
2 面
四、薄膜干涉
薄膜干涉的应用(二)——镜头镀膜
增透膜
(1)为了减少光学装置中的反射光的能量损失,可在元件表面涂一层透明薄膜,一般是氟化镁.
(2)如图所示,在增透膜的前后表面反射的两列光波形成相干波,相互叠加,当光程差为半波长的奇数倍时,在两个表面反射的光产生相消干涉,反射光的能量几乎等于零.
增透膜的最小厚度:增透膜厚度d=
(k=0,1,2,3,…),最小厚度为(λ为光在介质中传播时的波长).
四、薄膜干涉
薄膜干涉的应用(二)——镜头镀膜
镜头镀膜:在透镜表面涂上一层薄膜,薄膜的前后表面反射的两列光波形成相干光源,相互叠加,
(增透膜):当光程差为半波长的奇数倍时,在两个表
面反射的光相互抵消,反射光的能量几乎为零,透射光增强;
(增反膜):当光程差为半波长的偶数倍时,在
两个表面反射的光相互增强,反射光的能量增强,透射光减弱。
增透膜的厚度
四、薄膜干涉
薄膜干涉的应用(二)——镜头镀膜
思考 ①若增透膜的厚度为d,光在该种介质中的波长为λ,那么d 和λ应满足什么关系?
②若增反膜的厚度为d,光在该种介质中的波长为λ,那么d和λ应满足什么关系?
四、薄膜干涉
薄膜干涉的应用(三)—— 牛顿环
用一个曲率半径很大的凸透镜的凸面和一平面玻璃接触,在日光下或用白光照射时,可以看到接触点为一暗点,其周围为一些明暗相间的彩色圆环;而用单色光照射时,则表现为一些明暗相间的单色圆圈。
中央疏、边沿密的同心圆环
四、薄膜干涉
光从薄膜的前后两个表面反射出来两列光波,这两列光波的频率相同,产生干涉。
目标二:
干涉条纹和光的波长之间的关系
目标一:光的双缝干涉
光的干涉
目标三:
薄膜干涉
x = λ
干涉原理
应用
增透膜和增反膜
检查平面的平整度
步调相同
实验现象
干涉条件
相干光源
亮暗条纹条件
路程差为半波长偶数倍
——亮条纹
路程差为半波长奇数倍
——暗条纹
频率相同、振动方向相同、相位差恒定
课堂小结
第四章 光及其应用
粤教版 选择性必修一
第四节 光的干涉
新课导入
这些彩色条纹或图样是怎样形成的?
肥皂泡看起来常常是彩色的
雨后公路积水,上面漂浮的油膜也经常显现出彩色条纹或图样
牛顿 微粒说
光的本性学说的发展史
惠更斯 波动说
干涉现象是波动独有的特征,如果光真的是一种波,就必然会观察到光的干涉现象
知识回顾
机械波的干涉
2、产生干涉的条件
1、解释干涉现象
3、重叠区内一质点振动是加强还是减弱,取决于什么?
水波的干涉
知识回顾
机械波的干涉
水波的干涉
两列频率相同,振动方向相同,相位差恒定的两列波叠加,使某些区域的振动始终加强(波峰与波峰、波谷与波谷叠加),某些区域的振动始终减弱(波峰与波谷叠加),并且振动加强和振动减弱的区域相互间隔这种现象叫做波的干涉,形成的图样叫做干涉图样。
干涉现象是波动独有的特征,如果光真的是一种波,就必然会观察到光的干涉现象
思考1:光要发生干涉现象需要满足什么条件?
思考2:有没有什么方法可以获得相干光—频率相同的光呢?
相干光源(频率和振动情况一致)
一、光的双缝干涉现象
一、光的双缝干涉现象
天才的设想
光束
单缝
双缝
红滤色片
(激光)
屏幕
s0
s1
s2
托马斯·杨
杨氏双缝实验被评为十大最美丽实验之一。
巧妙解决了相干光问题
一、光的双缝干涉现象
1、装置特点:
1)双缝到单缝的距离相等
2)双缝很近 d=0.1mm
2、单缝作用:
获得线光源,使光源有唯一的频率和振动情况.
3、双缝作用:
获得两个频率相同、振动情况完全相同的光源,叫相干光源
一、光的双缝干涉现象
单缝
双缝
S1
S
S2
屏
杨氏双缝干涉实验证明了光是一种波
1801年,英国物理学家托马斯·杨在实验室里成功的观察到光的干涉
一、光的双缝干涉现象
等间距
4、双缝干涉图样特点:
中央亮条纹
明暗相间
单缝
双缝
S1
S
S2
屏
二、对光的双缝干涉现象的解释
1.干涉图样的特点:
S1
S2
双缝
屏幕
P0 中央亮纹
由于S1S2到中央亮纹的距离是相等的, 又由于从S1S2发出的光是振动情况完全相同,那么,当其中一条光线传来的是波峰时,另一条传来的也一定是波峰,其中一条光线传来的是波谷时,另一条传来的也一定是波谷,在P0点总是波峰与波峰相遇或波谷与波谷相遇,振幅A=A1+A2为最大,P点总是振动加强的地方,故出现亮纹。
光程差δ=S2P0-S1P0=0
S1
S2
P0
二、对光的双缝干涉现象的解释
第一条亮纹的形成原因分析
光程差δ=S2P1-S1P1=λ
P1
第一亮纹
双缝
S1
S2
屏幕
S1
S2
P1
λ
λ
δ=λ
取P0点上方的点P1,若从S1S2发出的光到P1点的光程差,正好等于一个波长
δ = S2P1-S1P1=λ,则当其中一条光线传来的是波峰时,另一条传来的也一定是波峰,其中一条光传来的是波谷时,另一条传来的也一定是波谷,在P1点总是波峰与波峰相遇或波谷与波谷相遇,振幅A=A1+A2为最大,P1点总是振动加强的地方,故出现亮纹。
二、对光的双缝干涉现象的解释
P2
第二亮纹
2λ
第二条亮纹的形成原因分析
光程差δ=S2P2-S1P2=2λ
双缝
S1
S2
屏幕
二、对光的双缝干涉现象的解释
双缝
S1
S2
屏幕
P1 第一亮纹 δ=λ
P0 中央亮纹 δ=0
P2 第二亮纹 δ=2λ
P3 第三亮纹 δ=3λ
当光程差δ= k λ 时出现亮纹
以此类推
光程差 δ=S2Pk-S1Pk=kλ
P3 / 第三亮纹 δ= - 3λ
P2/ 第二亮纹 δ= - 2λ
P1/ 第一亮纹 δ= - λ
二、对光的双缝干涉现象的解释
当其中一条光传来的是波峰,另一条传来的就是波谷,其中一条光传来的是波谷,另一条传来的一定是波峰,Q1点总是波峰与波谷相遇,振幅最小,Q1点总是振动减弱的地方,故出现暗纹。
2.暗条纹形成的原因
取P0点上方的点Q1,与两个狭缝S1、S2光程差δ= S1Q1-S2Q1=λ/2
Q1
第一暗纹
双缝
S1
S2
屏幕
光程差 δ=S2Q1-S1Q1= /
二、对光的双缝干涉现象的解释
取P0点上方的点Q2,与两个狭缝S1、S2光程差δ= S1-S2=3λ/2
当其中一条光传来的是波峰,另一条传来的就是波谷,其中一条光线传来的是波谷,另一条传来的一定是波峰,Q2点总是波峰与波谷相遇,振幅最小,Q2点总是振动减弱的地方,故出现暗纹。
Q1
第一暗纹
双缝
S1
S2
屏幕
Q2
第二暗纹
光程差 δ=S2Q1-S1Q1=3 /
二、对光的双缝干涉现象的解释
双缝
S1
S2
屏幕
Q1 第一暗纹 δ=λ/2
Q2 第二暗纹 δ=3λ/2
Q3 / 第三暗纹 δ= - 5λ/2
Q3 第三暗纹 δ=5λ/2
Q2/ 第二暗纹 δ= - 3λ/2
Q1/ 第一暗纹 δ= - λ/2
当光程差δ=(2k+1)λ /2 ,即半波长奇数倍时,出现暗纹。
以此类推
光程差 δ=S2Qk-S1Qk=(2k+1)λ /2
二、对光的双缝干涉现象的解释
中央亮条纹
明暗相间
二、对光的双缝干涉现象的解释
(1)空间的某点距离光源S1和S2的光程差为0、λ、2λ、3λ等波长的整数倍(半波长的偶数倍)时,该点为振动加强点。
(2)空间的某点距离光源S1和S2的光程差为λ /2、3 λ/2、5λ/2等半波长的奇数倍时,该点为振动减弱点。
3.总结规律
光程差 δ= kλ
( k=0,±1,± 2,……)
光程差 δ =(2k+1)λ/2 ( k=0,±1, ± 2,……)
暗纹
产生明、暗条纹的条件
亮纹:光程差 δ = kλ( k= 0,±1, ± 2, ……)
暗纹:光程差 δ =(2k+1)λ/2 (k=0, ± 1, ± 2,……)
亮纹
空气真空
三、干涉条纹与光的波长之间的关系
双缝
S1
S2
屏幕
x
x
条纹间距的含义:
相邻两条亮条纹(或暗条纹)中心之间的距离叫作条纹间距.
影响因素:双缝到屏的距离、双缝间的距离、入射光的波长
光的双缝干涉实验中,条纹间距的含义是什么?它可能与哪些因素有关?
三、干涉条纹与光的波长之间的关系
θ
公式推导
d:双缝间距
l:挡板到屏的距离
单色光
波长:λ
挡板
屏
d:双缝间距
l:挡板到屏的距离
在线段P1S2上作P1M=P1 S1
由几何知识得
r2-r1=d sin θ ①
x=l tan θ≈l sin θ ②
消去 sin θ
r2-r1=d
d l
条纹间距的公式推导
亮条纹:d = k λ (k = 0,±1,±2 …)
亮条纹中心的位置为:x = kλ
相邻两个亮条纹或暗条纹的中心间距是:
x = λ
三、干涉条纹与光的波长之间的关系
1.由数学知识可得条纹间距公式为 ,其中l为双缝到屏的距离,d为双缝间的距离,λ为入射光的波长.
2.单色光的干涉图样:干涉条纹是等间距的明暗相间的条纹.
红光干涉条纹
蓝光干涉条纹
单色光
波长:λ
挡板
屏
d:双缝间距
l:挡板到屏的距离
三、干涉条纹与光的波长之间的关系
(1)对于同一干涉装置和同一单色光,条纹之间的距离相等.
(2)对于不同颜色的光,波长不同,由 x = λ知条纹之间的距离与光
波的波长成正比.对于同一装置,所用光源的波长越长,条纹之间的距离越大,即用红光时条纹之间的距离 ,用紫光时条纹之间的距离 .
红光干涉条纹
紫光干涉条纹
蓝光干涉条纹
最大
最小
对 x = λ 公式的理解
λ 增大
三、干涉条纹与光的波长之间的关系
如果用白光做双缝干涉实验,会得到怎样的干涉条纹?为什么?
(1)明暗相间的彩色条纹;
(2)中央为白色亮条纹;
(3)干涉条纹是以中央亮纹为对称点排列的;
(4)在每条彩色亮纹中红光总是在外侧,紫光在内侧。
条纹间距与光波的波长成正比
红光条纹间距最大,紫光条纹间距最小
课堂练习
1.如图所示,用频率为f的单色光(激光)垂直照射双缝,在光屏的P点出现第2条暗条纹,已知光速为c,则P到双缝S1、S2的距离之差|r1-r2|应为( )
B
课堂练习
2.如图是杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,P1为第一级亮纹的中心,若将双缝间的距离变小,其他条件不变,则( )
A.屏上干涉条纹的间距将变小
B.屏上O点仍然为中央亮条纹的中心
C.屏上P1位置仍然可能为亮条纹的中心
D.屏上P1位置可能为暗条纹的中心
BD
四、薄膜干涉
观察到灯焰的像出现了明暗相间的干涉条纹。该条纹是由液膜前后两个面反射的光相互叠加发生干涉形成的。
在酒精灯的灯芯上撒一些食盐,灯焰就能发出明亮的黄光。把铁丝圈在肥皂水中蘸一下,让它挂上一层薄薄的液膜。把这层液膜当作一个平面镜,用它观察灯焰的像。这个像与直接看到的灯焰有什么不同?请解析看到的现象。
四、薄膜干涉
四、薄膜干涉
2.现象解释
由于重力的作用,肥皂薄膜将形成上薄下厚的楔形。
光从薄膜的前后两个表面反射出来两列光波,这两列光波的频率相同,产生干涉。
前表面
后表面
四、薄膜干涉
光程差为波长的整数倍,形成亮条纹。
光程差为半波长的奇数倍,形成暗条纹。
白光照射时是彩色条纹
四、薄膜干涉
薄膜干涉的应用(一)——检查表面的平整程度
利用薄膜干涉检查平面的平整度:如图甲所示,在利用薄膜干涉检查平面的平整度时,在被检查平面与透明样板间垫一个薄片,使其间形成一个楔形的空气薄层。
样板下表面
工件上表面
空气薄膜
注:薄片厚度一般仅为零点零几毫米左右,只相当于一张纸片的厚度
四、薄膜干涉
薄膜干涉的应用(一)——检查表面的平整程度
当用单色光从上面照射时,入射光从空气层的上、下表面反射出两列光波,于是从反射光中看到干涉条纹。如果被测表面是平整的,得到的干涉图样必是一组 的直线;
如果观察到的干涉条纹不平行,则表示被检测表面微有凸起或凹下,这些凸起或凹下的地方的干涉条纹就弯曲。
平行
被测表面有凹下,亮条纹提前出现
被测表面有凸起,亮条纹延后出现
练习与应用
劈尖干涉是一种薄膜干涉,如图所示。将一块平板玻璃放置在另一平板玻璃之上,在一端夹入两张纸片,从而在两玻璃表面之间形成一个劈形空气薄膜,当光从上方入射后,从上往下看到的干涉条纹有如下特点:
(1)任意一条明条纹或暗条纹所在位置下面的薄膜厚度相等;
(2)任意相邻明条纹或暗条纹所对应的薄膜厚度差恒定。
现若在如图所示装置中抽去一张纸片,则当光入射到劈形空气薄膜后,从上往下可以观察到干涉条纹发生了怎样的变化?
3 面
4 面
1 面
2 面
d1
d2
l
θ
θ
两处光程差为 1=2d1, 2=2d2
2- 1= ,所以d2-d1= /2
由几何关系可得
即
结论:
当抽去一张纸片时,θ减小, l增大,即条纹变稀疏。
亮纹1
亮纹2
3 面
4 面
1 面
2 面
四、薄膜干涉
薄膜干涉的应用(二)——镜头镀膜
增透膜
(1)为了减少光学装置中的反射光的能量损失,可在元件表面涂一层透明薄膜,一般是氟化镁.
(2)如图所示,在增透膜的前后表面反射的两列光波形成相干波,相互叠加,当光程差为半波长的奇数倍时,在两个表面反射的光产生相消干涉,反射光的能量几乎等于零.
增透膜的最小厚度:增透膜厚度d=
(k=0,1,2,3,…),最小厚度为(λ为光在介质中传播时的波长).
四、薄膜干涉
薄膜干涉的应用(二)——镜头镀膜
镜头镀膜:在透镜表面涂上一层薄膜,薄膜的前后表面反射的两列光波形成相干光源,相互叠加,
(增透膜):当光程差为半波长的奇数倍时,在两个表
面反射的光相互抵消,反射光的能量几乎为零,透射光增强;
(增反膜):当光程差为半波长的偶数倍时,在
两个表面反射的光相互增强,反射光的能量增强,透射光减弱。
增透膜的厚度
四、薄膜干涉
薄膜干涉的应用(二)——镜头镀膜
思考 ①若增透膜的厚度为d,光在该种介质中的波长为λ,那么d 和λ应满足什么关系?
②若增反膜的厚度为d,光在该种介质中的波长为λ,那么d和λ应满足什么关系?
四、薄膜干涉
薄膜干涉的应用(三)—— 牛顿环
用一个曲率半径很大的凸透镜的凸面和一平面玻璃接触,在日光下或用白光照射时,可以看到接触点为一暗点,其周围为一些明暗相间的彩色圆环;而用单色光照射时,则表现为一些明暗相间的单色圆圈。
中央疏、边沿密的同心圆环
四、薄膜干涉
光从薄膜的前后两个表面反射出来两列光波,这两列光波的频率相同,产生干涉。
目标二:
干涉条纹和光的波长之间的关系
目标一:光的双缝干涉
光的干涉
目标三:
薄膜干涉
x = λ
干涉原理
应用
增透膜和增反膜
检查平面的平整度
步调相同
实验现象
干涉条件
相干光源
亮暗条纹条件
路程差为半波长偶数倍
——亮条纹
路程差为半波长奇数倍
——暗条纹
频率相同、振动方向相同、相位差恒定
课堂小结
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
