1.3 洛伦兹力 课件(40张PPT)
文档属性
| 名称 | 1.3 洛伦兹力 课件(40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-19 10:25:35 | ||
图片预览









文档简介
(共40张PPT)
第一章 磁场
粤教版 选择性必修一
第三节 洛伦兹力
知识回顾
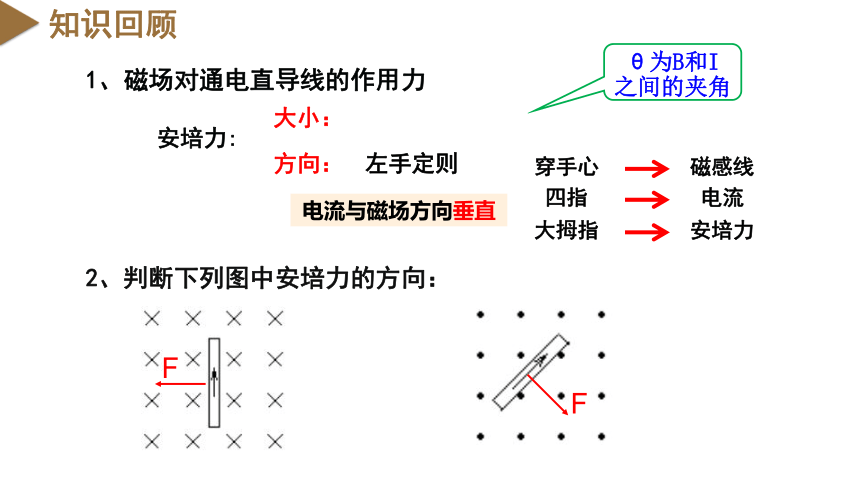
2、判断下列图中安培力的方向:
F
F
方向:
安培力:
1、磁场对通电直导线的作用力
θ为B和I
之间的夹角
大小:
左手定则
四指
穿手心
大拇指
电流
磁感线
安培力
电流与磁场方向垂直
知识回顾
磁场对通电导线(电流)有力的作用,而电流是电荷的定向运动形成的,由此你会想到了什么?
磁场可能对运动电荷有力的作用
导体中的电流是由电荷的定向移动产生的:I=nqSv
3、电流是如何形成的?
【演示实验】
观察阴极射线在磁场中的偏转
如图所示的玻璃管已经抽成真空。当左右两个电极按图示的极性连接到高压电源时,阴极会发射电子。电子在电场的加速下飞向阳极。挡板上有一个扁平的狭缝,电子飞过挡板后形成一个扁平的电子束。长条形的荧光板在阳极端稍稍倾向轴线,电子束掠射到荧光板上,显示出电子束的径迹。
阴极
阳极
狭缝
荧光板
电子束
阴极射线管的原理:
从阴极发射出来的电子,在阴阳两极间的高压作用下,使其加速,形成电子束,轰击到长条形的荧光屏上激发出荧光,可以显示电子束的运动轨迹。
实验观察:磁场对运动电荷的作用力
实验观察:磁场对运动电荷的作用力
当没有外磁场时,阴极射线管中的电子束沿直线前进;
当磁场方向与电子束前进方向垂直时,电子束运动径迹发生了弯曲,表明磁场对电子束产生了作用力。
当磁场的方向发生变化时,电子流的弯曲方向也发生了改变
实验现象:
实验结论:
1、磁场对运动电荷有力的作用
2、磁场对运动电荷力的方向与磁场的方向及电荷的运动方向有关
运动电荷在磁场中所受的力——洛伦兹力
1895年,荷兰物理学家洛伦兹公布了磁场对运动电荷的作用力的公式。为了纪念他,人们将磁场对运动电荷的作用力称为洛伦兹力。
一、认识洛伦兹力
安培力
洛伦兹力
磁场对电流的作用
磁场对运动电荷的作用
因
果
微观原因
宏观表现
安培力是洛伦兹力的宏观表现
洛伦兹力是安培力的微观本质
1、定义
2、洛伦兹力与安培力的关系
二、洛伦兹力的方向
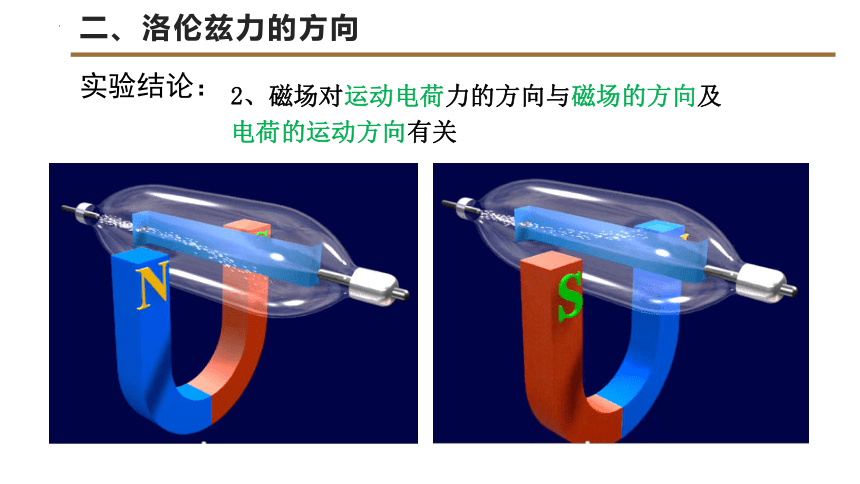
实验结论:
2、磁场对运动电荷力的方向与磁场的方向及电荷的运动方向有关
二、洛伦兹力的方向
向上偏转
向下偏转
二、洛伦兹力的方向
当运动电荷的速度方向与磁场平行时,运动电荷不受洛伦兹力;当运动电荷的速度方向与磁场垂直时,运动电荷受到的洛伦兹力,其方向即与磁场方向垂直,又与速度方向垂直。
进一步实验表明,电子偏转方向与磁场方向、电子运动方向有关。
类比安培力方向的判断方向,洛伦兹力方向也可以运用左手定则进行判断。
二、洛伦兹力的方向
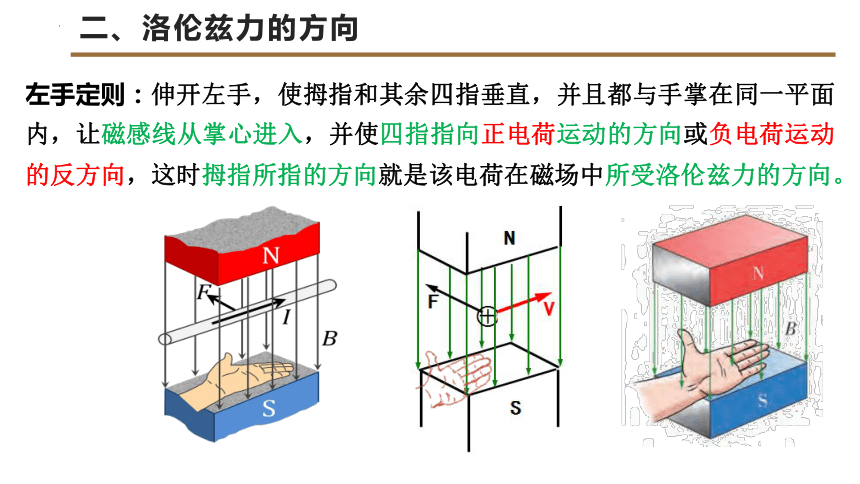
左手定则:伸开左手,使拇指和其余四指垂直,并且都与手掌在同一平面内,让磁感线从掌心进入,并使四指指向正电荷运动的方向或负电荷运动的反方向,这时拇指所指的方向就是该电荷在磁场中所受洛伦兹力的方向。
伸开左手:
磁感线——垂直穿入手心
四指——
大拇指——所受洛伦兹力的方向
①指向正电荷的运动方向
②指向负电荷运动的反向
v
F
v
F
二、洛伦兹力的方向
左手定则:
V
v1
v2
V
B
B
F
+
F
洛伦兹力F 与v、B三者之间的方向关系
+
F既与B垂直又与v垂直,即垂直于B和v所确定的平面,但B与v不一定垂直
洛伦兹力对电荷不做功,只改变粒子速度的方向,不改变粒子速度的大小。
× × ×
× × ×
× × ×
+
× × ×
× × ×
× × ×
v
v
+
v
v
v
+
v
FL
+
v
垂直纸面向外
垂直纸面向里
+
v
FL
FL
FL
FL=0
FL=0
例:试判断下图中的带电粒子刚进入磁场时所受的洛伦兹力的方向
例1:试判断下图中各带电粒子所受洛伦兹力的方向或带电粒子的运动方向。
f
v
v
v
f 垂直纸面向外
例2.将含有大量正、负带电粒子及不带电粒子的气体以一定速度垂直于磁场喷入匀强磁场中,它们在磁场中的运动径迹分成了如图所示的三束,其中②是直线。则( )
A ①是带正电的粒子
B ②是带正电的粒子
C ③是带正电的粒子
D ③是不带电的粒子
【解析】根据左手定则可知,①是带正电的粒子,A正确;②是不带电的粒子,B错误;根据左手定则可知,③是带负电的粒子,C、D错误。故选A。
A
三、洛伦兹力的大小
安培力是洛伦兹力的宏观表现
通电导线处于磁感应强度为B的匀强磁场中,导线中电流方向与磁场方向垂直。若只考虑其中一段长度为L的导线,设该段导线内定向移动的电荷数为N,导线所受安培力为F,每个电荷所受洛伦兹力为 f
如何利用安培力表达式推导洛伦兹力表达式呢?
洛伦兹力表达式的推导
其中Q为时间t内经过导线横截面积S的电量
根据安培力表达式,有
根据电流公式,有
设自由电荷定向移动的速度为v,每个电荷所带电量为q,则
导线中每个定向移动的电荷所受洛伦兹力的大小为
设该段导线内定向移动的电荷数为N,导线所受安培力为F,每个电荷所受洛伦兹力为 f
三、洛伦兹力的大小
大量实验证实,这一结果同样适用于带电粒子在磁场中运动的情况。
当电荷在垂直磁场的方向上运动(v⊥B)时,电荷所受的洛伦兹力为
导线中每个定向移动的电荷所受洛伦兹力的大小为
问题:若带电粒子不垂直射入磁场,电子受到的洛伦兹力又如何呢?
问题:若带电粒子不垂直射入磁场,电子受到的洛伦兹力又如何呢?
为B和v之间的夹角
v
B//
B
┴
v
v
v//
┴
B
三、洛伦兹力的大小
当电荷在垂直磁场的方向上运动(v⊥B)时,电荷所受的洛伦兹力为
当电荷运动的方向与磁场的方向夹角为θ 时,电荷所受的洛伦兹力为
当电荷在平行磁场的方向上运动(v//B)时,电荷所受的洛伦兹力为
当电荷静止于磁场中时( v =0): (即静止电荷不受洛伦兹力)
如图所示,各图中匀强磁场的磁感应强度均为B,带电粒子的速率均为 v,所带电量均为 q,试求出各图中带电粒子所受洛伦兹力的大小,并标出洛伦兹力的方向。
大小为qvB
方向垂直于v指向左上方
大小为1/2qvB
方向为垂直纸面向里
大小为qvB
方向垂直纸面向里
大小为qvB
垂直于v指向左上方
课堂练习
洛伦兹力和电场力的比较:
比较项目 洛伦兹力F 电场力F
性 质
产生条件
大 小
磁场对在其中运动电荷的作用力
电场对放入其中电荷的作用力
v≠ 0且v不与B平行
电场中的电荷一定受到电场力作用
F =qvB(v⊥B)
F =qE
力方向与场 方向的关系
做功情况
力F为零时 场的情况
作用效果
一定是F⊥B,F⊥v
正电荷与电场方向相同,
负电荷与电场方向相反
任何情况下都不做功
可能做正功、负功或不做功
F为零,B不一定为零
F为零,E一定为零
只改变电荷运动的速度方向,不改变速度大小
既可以改变电荷运动的速度大小,也可以改变电荷运动的方向
如图所示,有一磁感应强度为B、方向竖直向上的匀强磁场,一束电子束以初速度v从水平方向射入磁场,为了使电子束经过磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,这个电场的场强大小和方向是( )
A.,竖直向上 B.,水平向左
C.Bv,垂直于纸面向里 D.Bv,垂直于纸面向外
C
-
v
B
课堂练习
(1)如图所示,带电粒子所受重力可忽略不计,粒子在两板间同时受到电场力和洛伦兹力,只有当二力平衡时,粒子才不发生偏转,沿直线从两板间穿过。
四、速度选择器
速度选择器
(1)如图所示,带电粒子所受重力可忽略不计,粒子在两板间同时受到电场力和洛伦兹力,只有当二力平衡时,粒子才不发生偏转,沿直线从两板间穿过。
(3)粒子匀速通过速度选择器的条件:
速度选择器两极板间距离极小,粒子稍有偏转,即打到极板上。
只有电场力和洛伦兹力平衡时,即qE=qvB,v=时,粒子才能沿直线匀速通过。
(2)粒子受力特点:
①不计重力。
②同时受方向相反的电场力和磁场力作用。
为了诊断病人的心脏功能和动脉中血液粘滞情况,可使用电磁流量计测量血管中血液的流速和流量。如图所示是电磁流量计测量血管中血液流速的示意图,使血管处于磁感应强度为B的匀强磁场中,测得血管两侧电压为U。已知血管的直径为d,假定血管中各处液体的流速v相同,忽略重力影响。
(1)管壁上点a和点b,哪一点的电势高?
(2)试求血管中血液的流速v。
(1)根据左手定则,在洛伦兹力作用下,正离子向管道a的一侧集中,则点a电势高于点b
(2)当正负离子受到电场力与洛伦兹力平衡时,离子不再偏移,此时ab间有稳定的电势差,形成一个匀强磁场,对血液中的带电粒子,有 qvB=qU/d
解得 v=U/Bd
课堂练习
宇宙射线
从太阳或其他星体上,时刻都有大量的高能粒子流放出,称为宇宙射线。这些高能粒子流若都到达地球,将对地球上的生物带来危害。
但由于地球周围存在磁场,在洛伦兹力的作用下,改变了宇宙射线中带电粒子的运动方向,从而对宇宙射线起了一定的阻挡作用。
如图所示,来自太阳和其他星体的宇宙射线含有大量高能带电粒子,幸好由于地球磁场的存在而改变了这些带电粒子的运动方向,使很多带电粒子不能到达地面,避免了其对地面上生命的危害。
已知北京上空某处由南指北的磁感应强度为1.2×10-4T,如果有一速率为v=5.0×105m/s、电量q=1.6×10-19C的质子竖直向下运动穿过此处的地磁场。
(1)此时该质子受到的洛伦兹力是多大?向哪个方向偏转?
(2)在地球两极处地磁场方向可近似认为垂直于地面,
在赤道处地磁场方向可近似认为由地理南极指向地理
北极。那么,地球两极处和赤道处相比,哪个区域地
磁场对高能带电粒子的阻挡效果更好?为什么?
(1) f=qvB=9.6×10-18N
;质子向东偏转
(2)在赤道附近对宇宙射线的阻挡效果更强
课堂练习
极光
人类首次拍到南北极光“同放光彩”奇景
+
+
以正电荷为例
在太阳创造的诸如光和热等形式的能量中,有一种能量被称为“太阳风”。这是一束可以覆盖地球的强大的带电亚原子颗粒流,该太阳风在地球上空环绕地球流动,以大约每秒400公里的速度撞击地球磁场,磁场使该颗粒流偏向地磁极下落,它们与氧和氮的原子碰撞,击走电子,使之成为激发态的离子,这些离子发射不同波长的辐射,产生出红、绿或蓝等色的极光特征色彩,形成极光。
1、质量为0.1 g的小物块,带有5×10-4C的电量,放在倾角为30°的绝缘光滑斜面上,整个斜面置于0.5 T的匀强磁场中,磁场方向如图所示,物块由静止开始下滑,滑到某一位置时,物块开始离开斜面(设斜面足够长,g取10 m/s2,结果保留三位有效数字)。问:
(1)物块带电性质如何?
负电
(2)物块离开斜面时的速度为多少?
(3)物块在斜面上滑行的最大距离是多少?
课堂练习
2、如图所示,a为带正电的小物块,b是一不带电的绝缘物块(设a、b间无电荷转移),a、b叠放于粗糙的水平地面上,地面上方有垂直于纸面向里的匀强磁场。现用水平恒力F拉b物块,使a、b一起无相对滑动地向左做加速运动,则在加速运动阶段( )
A.a对b的压力不变
B.a对b的压力变大
C.a、b物块间的摩擦力变大
D.a、b物块间的摩擦力不变
B
课堂练习
3、如图所示,一带正电的物体固定在小车的底板上,其中底板绝缘,整个装置静止在水平地面上,在空间施加一垂直纸面向里的匀强磁场,如果保持小车不动,将匀强磁场沿水平方向向左匀速运动.
则下列说法正确的是( )
A.带电物体所受的洛伦兹力为零
B.带电物体受洛伦兹力且方向竖直向上
C.小车对地面的压力变大
D.地面对小车的摩擦力方向向左
B
课堂练习
4、如图所示,在磁感应强度为B的水平匀强磁场中,有一足够长的绝缘细棒OO′在竖直面内垂直磁场方向放置,细棒与水平面间的夹角为α,一质量为m、带电荷量为+q的圆环A套在OO′棒上,圆环与棒间的动摩擦因数为μ,且μ(1)圆环A的最大加速度为多大?获得最大加速度时的速度为多大?
(2)圆环A能够达到的最大速度为多大?
课堂练习
(1)由于μ环A沿棒运动的速度为v1时,
受到重力mg、洛伦兹力qv1B、棒的弹力FN1和摩擦力f1,f1=μFN1,
根据牛顿第二定律: mgsin α-f1=ma
垂直棒的方向有 FN1+qv1B=mgcos α
所以当FN1=0,即f1=0时,a有最大值am,
且am=gsin α,此时qv1B=mgcos α
解得v1=mgcosα/qB.
(2)设当环A的速度达到最大值vm时,
环受棒的弹力大小为FN2,方向垂直于棒向下,
摩擦力大小为f2=μFN2,
此时应有a=0,
即mgsin α=f2,FN2+mgcos α=qvmB
解得vm=mg(sin α+μcos α)/μqB.
5、如图所示,质量为m=1 kg、电荷量为q=5×10-2 C的带正电荷的小滑块,从半径为R=0.4 m的光滑固定绝缘1/4圆弧轨道上由静止自A端滑下.整个装置处在方向互相垂直的匀强电场与匀强磁场中.已知E=100 V/m,方向水平向右,B=1 T,方向垂直纸面向里,g=10 m/s2.
求:
(1)滑块到达C点时的速度;
(2)在C点时滑块所受洛伦兹力;
(3)在C点时滑块对轨道的压力.
课堂练习
解:(1)滑块从A点到C点的过程中洛伦兹力和支持力不做功,由动能定理得mgR-qER=1/2mvC2
vC=2m/s,方向水平向左
(2)滑块在C点时,根据洛伦兹力公式得:
f=qvCB=5×10-2×2×1 N=0.1 N,
方向竖直向下.
(3)在C点时,由牛顿第二定律得
FN-mg-qvCB=mvC2/R
则FN=mg+qvCB+mvC2/R=20.1 N
由牛顿第三定律可知,在C点时滑块对轨道的压力大小为20.1 N,方向竖直向下.
洛伦兹力与安培力的关系
①安培力是导体中所有定向移动的自由电荷受到的洛伦兹力的宏观表现,而洛伦兹力是安培力的微观本质.
②洛伦兹力对电荷不做功,但安培力却可以对导体做功.
③大小关系:F安=NF洛(N 是导体中运动的电荷数)
④方向关系:F安与F洛方向相同
⑤F安与F洛本质都是磁场对运动电荷的作用力
重点解析
第一章 磁场
粤教版 选择性必修一
第三节 洛伦兹力
知识回顾
2、判断下列图中安培力的方向:
F
F
方向:
安培力:
1、磁场对通电直导线的作用力
θ为B和I
之间的夹角
大小:
左手定则
四指
穿手心
大拇指
电流
磁感线
安培力
电流与磁场方向垂直
知识回顾
磁场对通电导线(电流)有力的作用,而电流是电荷的定向运动形成的,由此你会想到了什么?
磁场可能对运动电荷有力的作用
导体中的电流是由电荷的定向移动产生的:I=nqSv
3、电流是如何形成的?
【演示实验】
观察阴极射线在磁场中的偏转
如图所示的玻璃管已经抽成真空。当左右两个电极按图示的极性连接到高压电源时,阴极会发射电子。电子在电场的加速下飞向阳极。挡板上有一个扁平的狭缝,电子飞过挡板后形成一个扁平的电子束。长条形的荧光板在阳极端稍稍倾向轴线,电子束掠射到荧光板上,显示出电子束的径迹。
阴极
阳极
狭缝
荧光板
电子束
阴极射线管的原理:
从阴极发射出来的电子,在阴阳两极间的高压作用下,使其加速,形成电子束,轰击到长条形的荧光屏上激发出荧光,可以显示电子束的运动轨迹。
实验观察:磁场对运动电荷的作用力
实验观察:磁场对运动电荷的作用力
当没有外磁场时,阴极射线管中的电子束沿直线前进;
当磁场方向与电子束前进方向垂直时,电子束运动径迹发生了弯曲,表明磁场对电子束产生了作用力。
当磁场的方向发生变化时,电子流的弯曲方向也发生了改变
实验现象:
实验结论:
1、磁场对运动电荷有力的作用
2、磁场对运动电荷力的方向与磁场的方向及电荷的运动方向有关
运动电荷在磁场中所受的力——洛伦兹力
1895年,荷兰物理学家洛伦兹公布了磁场对运动电荷的作用力的公式。为了纪念他,人们将磁场对运动电荷的作用力称为洛伦兹力。
一、认识洛伦兹力
安培力
洛伦兹力
磁场对电流的作用
磁场对运动电荷的作用
因
果
微观原因
宏观表现
安培力是洛伦兹力的宏观表现
洛伦兹力是安培力的微观本质
1、定义
2、洛伦兹力与安培力的关系
二、洛伦兹力的方向
实验结论:
2、磁场对运动电荷力的方向与磁场的方向及电荷的运动方向有关
二、洛伦兹力的方向
向上偏转
向下偏转
二、洛伦兹力的方向
当运动电荷的速度方向与磁场平行时,运动电荷不受洛伦兹力;当运动电荷的速度方向与磁场垂直时,运动电荷受到的洛伦兹力,其方向即与磁场方向垂直,又与速度方向垂直。
进一步实验表明,电子偏转方向与磁场方向、电子运动方向有关。
类比安培力方向的判断方向,洛伦兹力方向也可以运用左手定则进行判断。
二、洛伦兹力的方向
左手定则:伸开左手,使拇指和其余四指垂直,并且都与手掌在同一平面内,让磁感线从掌心进入,并使四指指向正电荷运动的方向或负电荷运动的反方向,这时拇指所指的方向就是该电荷在磁场中所受洛伦兹力的方向。
伸开左手:
磁感线——垂直穿入手心
四指——
大拇指——所受洛伦兹力的方向
①指向正电荷的运动方向
②指向负电荷运动的反向
v
F
v
F
二、洛伦兹力的方向
左手定则:
V
v1
v2
V
B
B
F
+
F
洛伦兹力F 与v、B三者之间的方向关系
+
F既与B垂直又与v垂直,即垂直于B和v所确定的平面,但B与v不一定垂直
洛伦兹力对电荷不做功,只改变粒子速度的方向,不改变粒子速度的大小。
× × ×
× × ×
× × ×
+
× × ×
× × ×
× × ×
v
v
+
v
v
v
+
v
FL
+
v
垂直纸面向外
垂直纸面向里
+
v
FL
FL
FL
FL=0
FL=0
例:试判断下图中的带电粒子刚进入磁场时所受的洛伦兹力的方向
例1:试判断下图中各带电粒子所受洛伦兹力的方向或带电粒子的运动方向。
f
v
v
v
f 垂直纸面向外
例2.将含有大量正、负带电粒子及不带电粒子的气体以一定速度垂直于磁场喷入匀强磁场中,它们在磁场中的运动径迹分成了如图所示的三束,其中②是直线。则( )
A ①是带正电的粒子
B ②是带正电的粒子
C ③是带正电的粒子
D ③是不带电的粒子
【解析】根据左手定则可知,①是带正电的粒子,A正确;②是不带电的粒子,B错误;根据左手定则可知,③是带负电的粒子,C、D错误。故选A。
A
三、洛伦兹力的大小
安培力是洛伦兹力的宏观表现
通电导线处于磁感应强度为B的匀强磁场中,导线中电流方向与磁场方向垂直。若只考虑其中一段长度为L的导线,设该段导线内定向移动的电荷数为N,导线所受安培力为F,每个电荷所受洛伦兹力为 f
如何利用安培力表达式推导洛伦兹力表达式呢?
洛伦兹力表达式的推导
其中Q为时间t内经过导线横截面积S的电量
根据安培力表达式,有
根据电流公式,有
设自由电荷定向移动的速度为v,每个电荷所带电量为q,则
导线中每个定向移动的电荷所受洛伦兹力的大小为
设该段导线内定向移动的电荷数为N,导线所受安培力为F,每个电荷所受洛伦兹力为 f
三、洛伦兹力的大小
大量实验证实,这一结果同样适用于带电粒子在磁场中运动的情况。
当电荷在垂直磁场的方向上运动(v⊥B)时,电荷所受的洛伦兹力为
导线中每个定向移动的电荷所受洛伦兹力的大小为
问题:若带电粒子不垂直射入磁场,电子受到的洛伦兹力又如何呢?
问题:若带电粒子不垂直射入磁场,电子受到的洛伦兹力又如何呢?
为B和v之间的夹角
v
B//
B
┴
v
v
v//
┴
B
三、洛伦兹力的大小
当电荷在垂直磁场的方向上运动(v⊥B)时,电荷所受的洛伦兹力为
当电荷运动的方向与磁场的方向夹角为θ 时,电荷所受的洛伦兹力为
当电荷在平行磁场的方向上运动(v//B)时,电荷所受的洛伦兹力为
当电荷静止于磁场中时( v =0): (即静止电荷不受洛伦兹力)
如图所示,各图中匀强磁场的磁感应强度均为B,带电粒子的速率均为 v,所带电量均为 q,试求出各图中带电粒子所受洛伦兹力的大小,并标出洛伦兹力的方向。
大小为qvB
方向垂直于v指向左上方
大小为1/2qvB
方向为垂直纸面向里
大小为qvB
方向垂直纸面向里
大小为qvB
垂直于v指向左上方
课堂练习
洛伦兹力和电场力的比较:
比较项目 洛伦兹力F 电场力F
性 质
产生条件
大 小
磁场对在其中运动电荷的作用力
电场对放入其中电荷的作用力
v≠ 0且v不与B平行
电场中的电荷一定受到电场力作用
F =qvB(v⊥B)
F =qE
力方向与场 方向的关系
做功情况
力F为零时 场的情况
作用效果
一定是F⊥B,F⊥v
正电荷与电场方向相同,
负电荷与电场方向相反
任何情况下都不做功
可能做正功、负功或不做功
F为零,B不一定为零
F为零,E一定为零
只改变电荷运动的速度方向,不改变速度大小
既可以改变电荷运动的速度大小,也可以改变电荷运动的方向
如图所示,有一磁感应强度为B、方向竖直向上的匀强磁场,一束电子束以初速度v从水平方向射入磁场,为了使电子束经过磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,这个电场的场强大小和方向是( )
A.,竖直向上 B.,水平向左
C.Bv,垂直于纸面向里 D.Bv,垂直于纸面向外
C
-
v
B
课堂练习
(1)如图所示,带电粒子所受重力可忽略不计,粒子在两板间同时受到电场力和洛伦兹力,只有当二力平衡时,粒子才不发生偏转,沿直线从两板间穿过。
四、速度选择器
速度选择器
(1)如图所示,带电粒子所受重力可忽略不计,粒子在两板间同时受到电场力和洛伦兹力,只有当二力平衡时,粒子才不发生偏转,沿直线从两板间穿过。
(3)粒子匀速通过速度选择器的条件:
速度选择器两极板间距离极小,粒子稍有偏转,即打到极板上。
只有电场力和洛伦兹力平衡时,即qE=qvB,v=时,粒子才能沿直线匀速通过。
(2)粒子受力特点:
①不计重力。
②同时受方向相反的电场力和磁场力作用。
为了诊断病人的心脏功能和动脉中血液粘滞情况,可使用电磁流量计测量血管中血液的流速和流量。如图所示是电磁流量计测量血管中血液流速的示意图,使血管处于磁感应强度为B的匀强磁场中,测得血管两侧电压为U。已知血管的直径为d,假定血管中各处液体的流速v相同,忽略重力影响。
(1)管壁上点a和点b,哪一点的电势高?
(2)试求血管中血液的流速v。
(1)根据左手定则,在洛伦兹力作用下,正离子向管道a的一侧集中,则点a电势高于点b
(2)当正负离子受到电场力与洛伦兹力平衡时,离子不再偏移,此时ab间有稳定的电势差,形成一个匀强磁场,对血液中的带电粒子,有 qvB=qU/d
解得 v=U/Bd
课堂练习
宇宙射线
从太阳或其他星体上,时刻都有大量的高能粒子流放出,称为宇宙射线。这些高能粒子流若都到达地球,将对地球上的生物带来危害。
但由于地球周围存在磁场,在洛伦兹力的作用下,改变了宇宙射线中带电粒子的运动方向,从而对宇宙射线起了一定的阻挡作用。
如图所示,来自太阳和其他星体的宇宙射线含有大量高能带电粒子,幸好由于地球磁场的存在而改变了这些带电粒子的运动方向,使很多带电粒子不能到达地面,避免了其对地面上生命的危害。
已知北京上空某处由南指北的磁感应强度为1.2×10-4T,如果有一速率为v=5.0×105m/s、电量q=1.6×10-19C的质子竖直向下运动穿过此处的地磁场。
(1)此时该质子受到的洛伦兹力是多大?向哪个方向偏转?
(2)在地球两极处地磁场方向可近似认为垂直于地面,
在赤道处地磁场方向可近似认为由地理南极指向地理
北极。那么,地球两极处和赤道处相比,哪个区域地
磁场对高能带电粒子的阻挡效果更好?为什么?
(1) f=qvB=9.6×10-18N
;质子向东偏转
(2)在赤道附近对宇宙射线的阻挡效果更强
课堂练习
极光
人类首次拍到南北极光“同放光彩”奇景
+
+
以正电荷为例
在太阳创造的诸如光和热等形式的能量中,有一种能量被称为“太阳风”。这是一束可以覆盖地球的强大的带电亚原子颗粒流,该太阳风在地球上空环绕地球流动,以大约每秒400公里的速度撞击地球磁场,磁场使该颗粒流偏向地磁极下落,它们与氧和氮的原子碰撞,击走电子,使之成为激发态的离子,这些离子发射不同波长的辐射,产生出红、绿或蓝等色的极光特征色彩,形成极光。
1、质量为0.1 g的小物块,带有5×10-4C的电量,放在倾角为30°的绝缘光滑斜面上,整个斜面置于0.5 T的匀强磁场中,磁场方向如图所示,物块由静止开始下滑,滑到某一位置时,物块开始离开斜面(设斜面足够长,g取10 m/s2,结果保留三位有效数字)。问:
(1)物块带电性质如何?
负电
(2)物块离开斜面时的速度为多少?
(3)物块在斜面上滑行的最大距离是多少?
课堂练习
2、如图所示,a为带正电的小物块,b是一不带电的绝缘物块(设a、b间无电荷转移),a、b叠放于粗糙的水平地面上,地面上方有垂直于纸面向里的匀强磁场。现用水平恒力F拉b物块,使a、b一起无相对滑动地向左做加速运动,则在加速运动阶段( )
A.a对b的压力不变
B.a对b的压力变大
C.a、b物块间的摩擦力变大
D.a、b物块间的摩擦力不变
B
课堂练习
3、如图所示,一带正电的物体固定在小车的底板上,其中底板绝缘,整个装置静止在水平地面上,在空间施加一垂直纸面向里的匀强磁场,如果保持小车不动,将匀强磁场沿水平方向向左匀速运动.
则下列说法正确的是( )
A.带电物体所受的洛伦兹力为零
B.带电物体受洛伦兹力且方向竖直向上
C.小车对地面的压力变大
D.地面对小车的摩擦力方向向左
B
课堂练习
4、如图所示,在磁感应强度为B的水平匀强磁场中,有一足够长的绝缘细棒OO′在竖直面内垂直磁场方向放置,细棒与水平面间的夹角为α,一质量为m、带电荷量为+q的圆环A套在OO′棒上,圆环与棒间的动摩擦因数为μ,且μ
(2)圆环A能够达到的最大速度为多大?
课堂练习
(1)由于μ
受到重力mg、洛伦兹力qv1B、棒的弹力FN1和摩擦力f1,f1=μFN1,
根据牛顿第二定律: mgsin α-f1=ma
垂直棒的方向有 FN1+qv1B=mgcos α
所以当FN1=0,即f1=0时,a有最大值am,
且am=gsin α,此时qv1B=mgcos α
解得v1=mgcosα/qB.
(2)设当环A的速度达到最大值vm时,
环受棒的弹力大小为FN2,方向垂直于棒向下,
摩擦力大小为f2=μFN2,
此时应有a=0,
即mgsin α=f2,FN2+mgcos α=qvmB
解得vm=mg(sin α+μcos α)/μqB.
5、如图所示,质量为m=1 kg、电荷量为q=5×10-2 C的带正电荷的小滑块,从半径为R=0.4 m的光滑固定绝缘1/4圆弧轨道上由静止自A端滑下.整个装置处在方向互相垂直的匀强电场与匀强磁场中.已知E=100 V/m,方向水平向右,B=1 T,方向垂直纸面向里,g=10 m/s2.
求:
(1)滑块到达C点时的速度;
(2)在C点时滑块所受洛伦兹力;
(3)在C点时滑块对轨道的压力.
课堂练习
解:(1)滑块从A点到C点的过程中洛伦兹力和支持力不做功,由动能定理得mgR-qER=1/2mvC2
vC=2m/s,方向水平向左
(2)滑块在C点时,根据洛伦兹力公式得:
f=qvCB=5×10-2×2×1 N=0.1 N,
方向竖直向下.
(3)在C点时,由牛顿第二定律得
FN-mg-qvCB=mvC2/R
则FN=mg+qvCB+mvC2/R=20.1 N
由牛顿第三定律可知,在C点时滑块对轨道的压力大小为20.1 N,方向竖直向下.
洛伦兹力与安培力的关系
①安培力是导体中所有定向移动的自由电荷受到的洛伦兹力的宏观表现,而洛伦兹力是安培力的微观本质.
②洛伦兹力对电荷不做功,但安培力却可以对导体做功.
③大小关系:F安=NF洛(N 是导体中运动的电荷数)
④方向关系:F安与F洛方向相同
⑤F安与F洛本质都是磁场对运动电荷的作用力
重点解析
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
