2023--2024学年人教版九年级数学下册 综合练习(含答案)
文档属性
| 名称 | 2023--2024学年人教版九年级数学下册 综合练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 22:11:29 | ||
图片预览



文档简介
2023--2024学年人教版九年级数学下册综合练习
一.选择题(共12小题)
1.如图,点P是双曲线上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )
A.逐渐增大 B.逐渐减小
C.先增大后减小 D.保持不变
2.下列关系式中y是x的反比例函数的是( )
A.y=2x B.xy=1 C. D.
3.点A(﹣1,y1)与点B(﹣2,y2)均在双曲线y=﹣上,则y1、y2大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法比较
4.若两个相似三角形对应中线的比为,则这两个相似三角形的面积比为( )
A. B. C.9:2 D.2:9
5.如图,能使△ABC∽△ADE成立的条件是( )
A.∠A=∠A B.∠ADE=∠AED C. D.
6.如图,△ABC是等边三角形,点P是边BC上的一点;且CP>BP,以PC为边作等边△PCE.若△PAB的面积与△PCE的面积相等,则的值为( )
A. B. C. D.
7.如图,某滑雪场有一坡角为α的滑雪道,滑雪道AC的长为300m,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A.300cosαm B.300sinαm C. D.
8.△ABC中,∠A、∠B、∠C的对边分别为a、b、c.已知a=3,b=4,c=5,CD⊥AB,则cos∠BCD的值为( )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,AB=5,AC=4,下列四个选项,正确的是( )
A. B. C. D.
10.在下面四个几何体中,其左视图不是中心对称图形的是( )
A. B. C. D.
11.已知∠A+∠B=90°,且,则tanB的值为( )
A. B. C. D.
12.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G.则下列结论中错误的是( )
A.= B.= C.= D.=
二.填空题(共5小题)
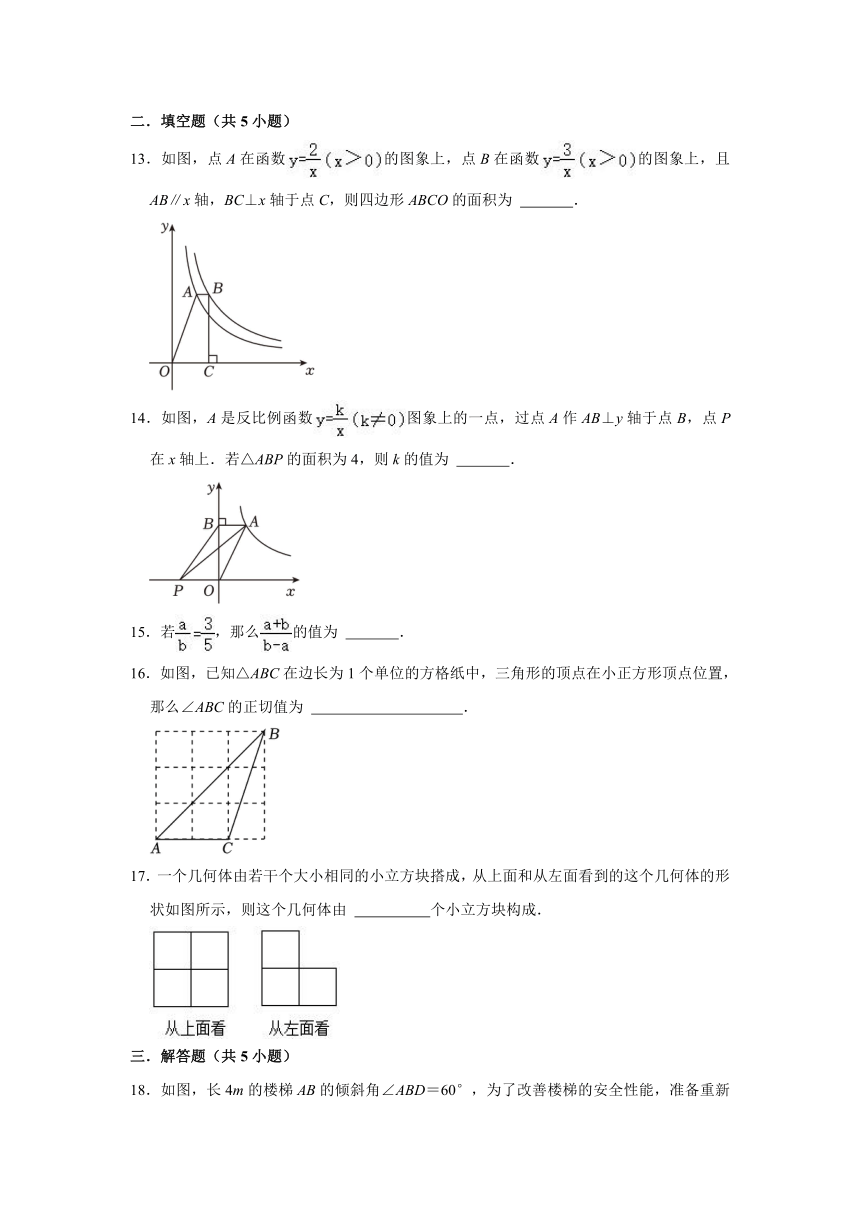
13.如图,点A在函数的图象上,点B在函数的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为 .
14.如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上.若△ABP的面积为4,则k的值为 .
15.若,那么的值为 .
16.如图,已知△ABC在边长为1个单位的方格纸中,三角形的顶点在小正方形顶点位置,那么∠ABC的正切值为 .
17.一个几何体由若干个大小相同的小立方块搭成,从上面和从左面看到的这个几何体的形状如图所示,则这个几何体由 个小立方块构成.
三.解答题(共5小题)
18.如图,长4m的楼梯AB的倾斜角∠ABD=60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD=37°,求调整后的楼梯AC的长(精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,).
19.如图,在Rt△ABC中,∠ACB为直角,CD⊥AB于D.在Rt△ADC中,E是AC的中点.ED的延长线与CB的延长线交于点F.
(1)求证:△FDC∽△FBD;
(2)若FD=6,FB=10,求BC的长.
20.如图,一次函数y=k1x+b(k1≠0)的图象与反比例函数y=(k2≠0)的图象交于点A(﹣1,n),与x轴交于点B(3,0),与y轴交于点C(0,3).
(1)求一次函数和反比例函数的表达式;
(2)已知P为反比例函数y=的图象上一点,满足S△POB=3S△AOC,求点P的坐标.
(3)在第四象限反比例函数y=的图象上是否存在点M,使点M绕点C顺时针旋转90°得到的对应点N恰好落在第二象限反比例函数y=的图象上?若存在,求点M的坐标;若不存在,说明理由.
21.如图,点D,E,F分别在△ABC三边上,且DE∥BC,EF∥AB,BD=3AD,BC=8.
(1)求CF的长;
(2)若△ADE的面积为4,求四边形BDEF的面积.
汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.5m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,求汽车盲区EB的长度.
参考答案
一.选择题(共12小题)
1--10DBADC BBCCC 11--12CD
二.填空题(共5小题)
13.2
14.8
15.4
16.
17.5或6
三.解答题(共5小题)
18.解:在Rt△ABD中,AB=4m,∠ABD=60°,
∵sin∠ABD=,
∴AD=AB sin∠ABD=4×=2(m),
在Rt△ACD中,∠ACD=37°,
则AC==≈≈5.8(m),
答:调整后的楼梯AC的长约为5.8m.
19.(1)证明:∵∠ACB为直角,CD⊥AB于点D,
∴∠ADC=∠ACB=90°,
∴∠FCD=∠A=90°﹣∠ACD,
∵E是AC的中点,
∴DE=AE=CE=AC,
∴∠FDB=∠EDA=∠A,
∴∠FCD=∠FDB,
∵∠F=∠F,
∴△FDC∽△FBD.
(2)解:∵△FDC∽△FBD
∴=,
∵FD=6,FB=10,
∴FC===18,
∴BC=FC﹣FB=18﹣10=8,
∴BC的长为8
20.解:(1)∵点B(3,0)C(0,3)在一次函数y=k1x+b图象上,
∴,
解得,
∴一次函数解析式为:y=﹣x+3,
∵A(﹣1,n)在一次函数图象上,
∴n=4,
∵A(﹣1,4)在反比例函数解析式上,
∴k2=﹣4,
∴反比例函数解析式为:y=﹣;
(2)设点P的坐标为(m,﹣),
∵A(﹣1,4),C(0,3),
∴S△AOC=×3×1=,
∴S△POB=3×=,
∵B(3,0),
∴OB=3,
∴S△POB=丨﹣丨=,
解得m=或﹣,
∴点P的坐标为(,﹣3)或(﹣,3).
(3)如图,作MF⊥y轴,垂足为F,作NE⊥y轴,垂足为F,
设点M坐标为(a,﹣),C(0,3),
在△NEC和△CFM中,
,
∴△NEC≌△CFM(AAS),
∴CE=FM=a,CF=NE=3+,
∴N(﹣3﹣,3﹣a),
若点N在反比例函数图象上,则有:
(3﹣a)(﹣3﹣)=﹣4,
整理得:3a2﹣a﹣12=0,
解得a=或a=(舍去),
∴点M的横坐标为,点M的纵坐标为:,
答:存在这样的点M,点M的坐标为(,).
21.解:(1)∵DE∥BC,
∴,
∴,
∵EF∥AB,
∴,
∵BC=8,
∴,
∴CF=BC﹣BF=6;
(2)∵DE∥BC,
∴∠AED=∠C,
∵EF∥AB,∠A=∠FEC,
∴△ADE∽△EFC.
∴,
∴S△EFC=9S△ADE=4×9=36,
∵DE∥BC,
∴∠ADB=∠B,且∠A=∠A,
∴△ADE∽△ABC,
∴,
∴S△ABC=16S△ADE=64,
∴S四边形BDEF=S△ABC﹣S△ADE﹣S△EFC=24.
22.解:如图,过点P作PN⊥EB于点N,交AF于点M.
∵3DF=2AF,AF=1.8m,
∴DF=1.2(m),
∵四边形ACDF是矩形,
∴∠FDC=90°,AF∥CD,
∴DF⊥DC,
∵MN⊥DC,
∴DF=MN=1.2(m),
∵PM=1.5m,
∴PM=PN﹣MN=1.5﹣1.2=0.3(m),
∵AF∥EB,
∴△PAF∽△PBE,
∴=,
∴=,
∴EB=9(m)
一.选择题(共12小题)
1.如图,点P是双曲线上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )
A.逐渐增大 B.逐渐减小
C.先增大后减小 D.保持不变
2.下列关系式中y是x的反比例函数的是( )
A.y=2x B.xy=1 C. D.
3.点A(﹣1,y1)与点B(﹣2,y2)均在双曲线y=﹣上,则y1、y2大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法比较
4.若两个相似三角形对应中线的比为,则这两个相似三角形的面积比为( )
A. B. C.9:2 D.2:9
5.如图,能使△ABC∽△ADE成立的条件是( )
A.∠A=∠A B.∠ADE=∠AED C. D.
6.如图,△ABC是等边三角形,点P是边BC上的一点;且CP>BP,以PC为边作等边△PCE.若△PAB的面积与△PCE的面积相等,则的值为( )
A. B. C. D.
7.如图,某滑雪场有一坡角为α的滑雪道,滑雪道AC的长为300m,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A.300cosαm B.300sinαm C. D.
8.△ABC中,∠A、∠B、∠C的对边分别为a、b、c.已知a=3,b=4,c=5,CD⊥AB,则cos∠BCD的值为( )
A. B. C. D.
9.在Rt△ABC中,∠C=90°,AB=5,AC=4,下列四个选项,正确的是( )
A. B. C. D.
10.在下面四个几何体中,其左视图不是中心对称图形的是( )
A. B. C. D.
11.已知∠A+∠B=90°,且,则tanB的值为( )
A. B. C. D.
12.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G.则下列结论中错误的是( )
A.= B.= C.= D.=
二.填空题(共5小题)
13.如图,点A在函数的图象上,点B在函数的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为 .
14.如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上.若△ABP的面积为4,则k的值为 .
15.若,那么的值为 .
16.如图,已知△ABC在边长为1个单位的方格纸中,三角形的顶点在小正方形顶点位置,那么∠ABC的正切值为 .
17.一个几何体由若干个大小相同的小立方块搭成,从上面和从左面看到的这个几何体的形状如图所示,则这个几何体由 个小立方块构成.
三.解答题(共5小题)
18.如图,长4m的楼梯AB的倾斜角∠ABD=60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD=37°,求调整后的楼梯AC的长(精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,).
19.如图,在Rt△ABC中,∠ACB为直角,CD⊥AB于D.在Rt△ADC中,E是AC的中点.ED的延长线与CB的延长线交于点F.
(1)求证:△FDC∽△FBD;
(2)若FD=6,FB=10,求BC的长.
20.如图,一次函数y=k1x+b(k1≠0)的图象与反比例函数y=(k2≠0)的图象交于点A(﹣1,n),与x轴交于点B(3,0),与y轴交于点C(0,3).
(1)求一次函数和反比例函数的表达式;
(2)已知P为反比例函数y=的图象上一点,满足S△POB=3S△AOC,求点P的坐标.
(3)在第四象限反比例函数y=的图象上是否存在点M,使点M绕点C顺时针旋转90°得到的对应点N恰好落在第二象限反比例函数y=的图象上?若存在,求点M的坐标;若不存在,说明理由.
21.如图,点D,E,F分别在△ABC三边上,且DE∥BC,EF∥AB,BD=3AD,BC=8.
(1)求CF的长;
(2)若△ADE的面积为4,求四边形BDEF的面积.
汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.5m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,求汽车盲区EB的长度.
参考答案
一.选择题(共12小题)
1--10DBADC BBCCC 11--12CD
二.填空题(共5小题)
13.2
14.8
15.4
16.
17.5或6
三.解答题(共5小题)
18.解:在Rt△ABD中,AB=4m,∠ABD=60°,
∵sin∠ABD=,
∴AD=AB sin∠ABD=4×=2(m),
在Rt△ACD中,∠ACD=37°,
则AC==≈≈5.8(m),
答:调整后的楼梯AC的长约为5.8m.
19.(1)证明:∵∠ACB为直角,CD⊥AB于点D,
∴∠ADC=∠ACB=90°,
∴∠FCD=∠A=90°﹣∠ACD,
∵E是AC的中点,
∴DE=AE=CE=AC,
∴∠FDB=∠EDA=∠A,
∴∠FCD=∠FDB,
∵∠F=∠F,
∴△FDC∽△FBD.
(2)解:∵△FDC∽△FBD
∴=,
∵FD=6,FB=10,
∴FC===18,
∴BC=FC﹣FB=18﹣10=8,
∴BC的长为8
20.解:(1)∵点B(3,0)C(0,3)在一次函数y=k1x+b图象上,
∴,
解得,
∴一次函数解析式为:y=﹣x+3,
∵A(﹣1,n)在一次函数图象上,
∴n=4,
∵A(﹣1,4)在反比例函数解析式上,
∴k2=﹣4,
∴反比例函数解析式为:y=﹣;
(2)设点P的坐标为(m,﹣),
∵A(﹣1,4),C(0,3),
∴S△AOC=×3×1=,
∴S△POB=3×=,
∵B(3,0),
∴OB=3,
∴S△POB=丨﹣丨=,
解得m=或﹣,
∴点P的坐标为(,﹣3)或(﹣,3).
(3)如图,作MF⊥y轴,垂足为F,作NE⊥y轴,垂足为F,
设点M坐标为(a,﹣),C(0,3),
在△NEC和△CFM中,
,
∴△NEC≌△CFM(AAS),
∴CE=FM=a,CF=NE=3+,
∴N(﹣3﹣,3﹣a),
若点N在反比例函数图象上,则有:
(3﹣a)(﹣3﹣)=﹣4,
整理得:3a2﹣a﹣12=0,
解得a=或a=(舍去),
∴点M的横坐标为,点M的纵坐标为:,
答:存在这样的点M,点M的坐标为(,).
21.解:(1)∵DE∥BC,
∴,
∴,
∵EF∥AB,
∴,
∵BC=8,
∴,
∴CF=BC﹣BF=6;
(2)∵DE∥BC,
∴∠AED=∠C,
∵EF∥AB,∠A=∠FEC,
∴△ADE∽△EFC.
∴,
∴S△EFC=9S△ADE=4×9=36,
∵DE∥BC,
∴∠ADB=∠B,且∠A=∠A,
∴△ADE∽△ABC,
∴,
∴S△ABC=16S△ADE=64,
∴S四边形BDEF=S△ABC﹣S△ADE﹣S△EFC=24.
22.解:如图,过点P作PN⊥EB于点N,交AF于点M.
∵3DF=2AF,AF=1.8m,
∴DF=1.2(m),
∵四边形ACDF是矩形,
∴∠FDC=90°,AF∥CD,
∴DF⊥DC,
∵MN⊥DC,
∴DF=MN=1.2(m),
∵PM=1.5m,
∴PM=PN﹣MN=1.5﹣1.2=0.3(m),
∵AF∥EB,
∴△PAF∽△PBE,
∴=,
∴=,
∴EB=9(m)
