4.5 垂线(第2课时) 课件(共29张PPT)
文档属性
| 名称 | 4.5 垂线(第2课时) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 14:28:15 | ||
图片预览






文档简介
(共29张PPT)
4.5 垂 线
第2课时 垂线段与点到直线的距离
1.掌握点到直线的距离的有关概念.
2.会作出直线外一点到一条直线的垂线.
3.理解垂线段最短的性质.
4.经过观察、分析、抽象、概括、画图等数学活动过程,进一步发展思维能力.
5.体会数学的应用价值.
【教学重点】
点到直线的距离的概念及垂线段最短的性质.
【教学难点】
垂线段最短的性质及从直线外一点作直线的垂线的画法.
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1. 垂线的定义
2. 垂线的性质
在同一平面内,垂直于同一条直线的两直线平行.
在同一平面内,如果一直线垂直于两条平行线中的一条,那么这条直线必垂直于另一条直线.
在灌溉时,要把河中的水引到农田 P 处,如何挖掘能使渠道最短?
河
课本P98“做一做”:(黑板上示范)
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点P画l的垂线,这样的垂线能画几条
(3)过直线l外的一点P画l的垂线,这样的垂线能画几条
.
l
.
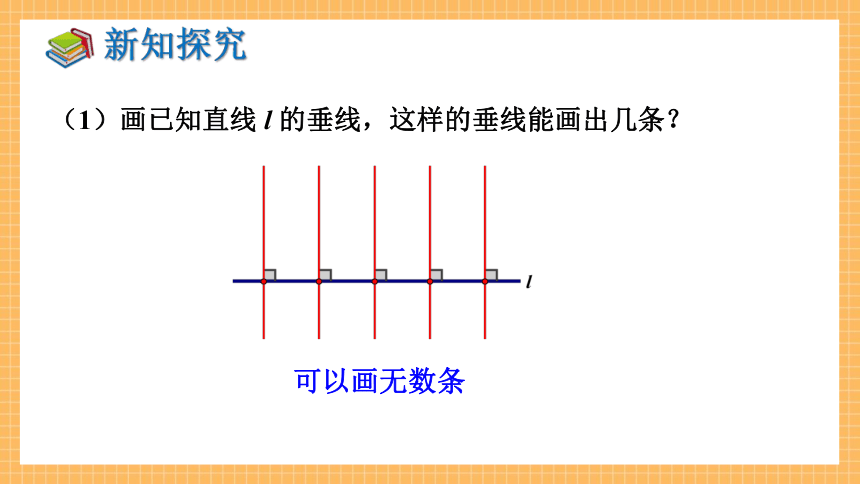
(1)画已知直线 l 的垂线,这样的垂线能画出几条?
可以画无数条
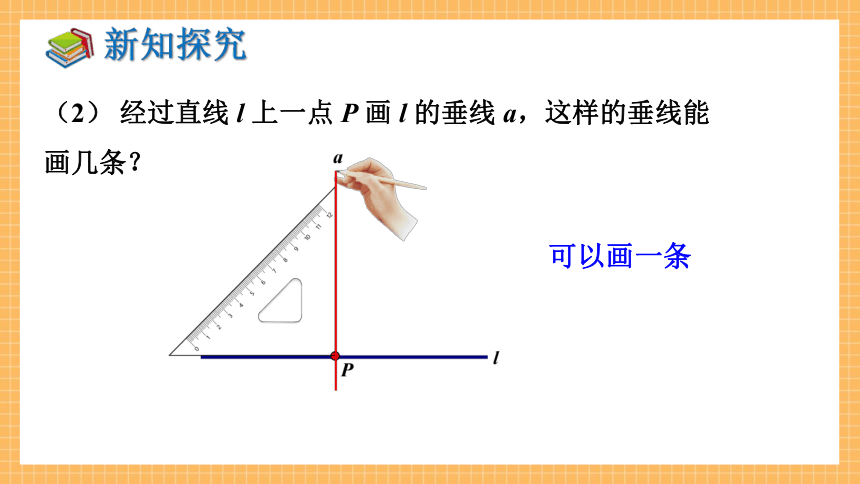
(2) 经过直线 l 上一点 P 画 l 的垂线 a,这样的垂线能画几条?
可以画一条
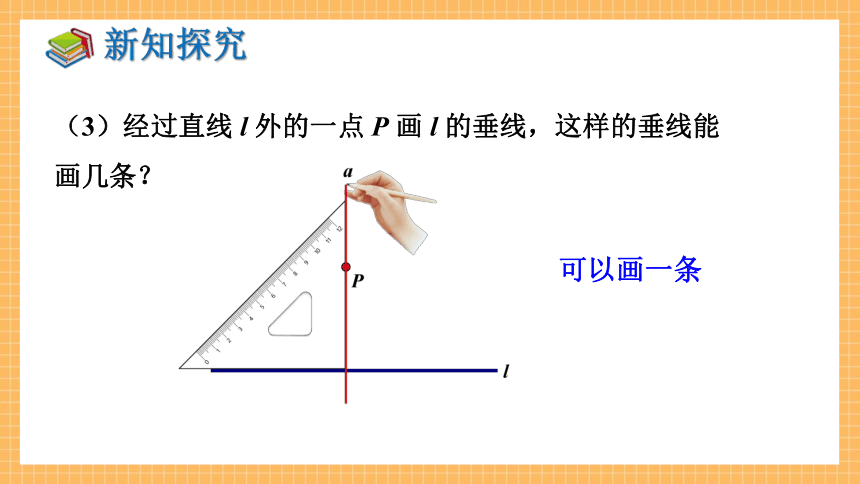
(3)经过直线 l 外的一点 P 画 l 的垂线,这样的垂线能画几条?
可以画一条
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
3.过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
1、如图,设PO垂直于直线l,O为垂足,线段PO叫作P点到直线l 的垂线段.
P
B
l
O
A
C
2、通过P点的其他直线交 l 于A、B、
C…,线段PA,PB,PC都不是垂线段,称为斜线段.
垂线与垂线段有何区别和联系?
区别:垂线是直线,垂线段是线段.
联系:垂线和垂线段都有垂直关系.
1. 线段 AB,AC,AD ,AE 谁最短?
2.你能用一句话表示这个结论吗?
说一说:
如图,从 A 点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
C
D
E
B
l
A
直线外一点与直线上各点连接的所有线段中,垂线段最短. 简单说成:垂线段最短.
线段 AD 的长度叫做点 A 到直线 l 的距离.
特别规定:
D
l
A
在灌溉时,要把河中的水引到农田 P 处,如何挖掘能使渠道最短?请画出图来,并说明理由.
河
垂线段最短
【例3】如图,在三角形 ABC 中,∠ABC = 90°,BD⊥AC, 垂足为 D,AB = 5,BC = 12,AC = 13.
求:(1)点 A 到直线 BC 的距离;(2)点 B 到直线 AC 的距离.
解(1) 因为∠ABC = 90°,
所以 AB⊥BC, B为垂足.
所以线段 AB 即为点 A 到直线 BC 的垂线段.
因为AB = 5,
所以点 A 到直线 BC 的距离为 5.
(2)因为BD⊥AC
所以线段BD的长度点B到直线AC的距离.
所以点B到直线AC的距离为 .
如图,三角形 ABC 中,∠C=90°.
(1)分别指出点 A 到直线 BC,
点 B 到直线 AC 的距离是哪些
线段的长;
(2)三条边 AB、AC、BC 中
哪条边最长?为什么?
AC
BC
理由:连接直线外一点与直线上各点的所有线段中,垂线段最短.
AB.
1.如图,
①过点 Q 作 QD⊥AB,垂足为 D,
②过点 P 作 PE⊥AB,垂足为 E,
③过点 Q 作 QF⊥AC,垂足为 F,
④连 P、Q 两点,
⑤ P、Q 两点间的距离是线段______的长度,
⑥点 Q 到直线 AB 的距离是线段_______的长度,
⑦点 Q 到直线 AC 的距离是线段_______的长度,
⑧点 P 到直线 AB 的距离是线段________的长度.
解:①②③④ 作图如图所示
PQ
QD
QF
PE
2. 过点 P 向线段 AB 所在直线引垂线,正确的是( )
A B C D
C
3.如图,已知AC⊥BC于点C,CD⊥AB于点D,亮亮总结出了如下结论:
①线段AC的长,表示点A到直线BC的距离;
②线段CD的长,表示点C到直线AB的距离;
③线段AD的长,表示点A到直线CD的距离;
④∠ACD是∠BCD的余角.
亮亮总结的结论正确的有( )个.
A.1 B.2 C.3 D.4
C
4. 如图,AC⊥BC,∠CDB = 90°,线段 AC、BC、CD 中最短的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
5. P 是直线 AB 外一点,过点 P 作 PO⊥AB,垂足为 O,若 C 为直线 AB 上任意一点,则线段 PC 与线段 PO 的大小关系是( )
A. PC > PO B. PC < PO
C. PC ≥ PO D. PC ≥ PO
C
6. 如图,∠C = 90°,AB = 5,AC = 4,BC = 3,则点 A 到直线 BC 的距离为_____,点 B 到直线 AC 的距离为______,A、B 间的距离为______.
4
3
5
7. 下列说法正确的是( )
A. 线段 AB 叫做点 B 到直线 AC 的距离
B. 线段 AB 的长度叫做点 A 到直线 AC 的距离
C. 线段 BD 的长度叫做点 D 到直线 BC 的距离
D. 线段 BD 的长度叫做点 B 到直线 AC 的距离
A
B
C
D
D
8. 如图,在直角三角形 ABC 中,∠A = 90 °,AB = 3 cm,AC = 4 cm,BC = 5 cm,求点 A 到 BC 的距离,点 C 到 AB 的距离.
解: 点 A 到 BC 的距离是 cm.
点 C 到 AB 的距离是 4 cm.
9. 一辆汽车在直线形的公路 AB 上由 A 向 B 行驶,C、D 是分别位于公路 AB 两侧的加油站.
(1)设汽车行驶到公路 AB 上点 M 的位置时,距离加油站 C 最近;行驶到点 N 的位置时,距离加油站 D 最近,请在图中分别画出点 M、N 的位置;
A
B
C
D
M
N
(2)当汽车从 A 出发向 B 行驶时,在公路 AB 的哪一段路上距离 C、D 两加油站都越来越近?在哪一段路上距离加油站 D 越来越近,而离加油站 C 却越来越远?
解:在公路 AB 的 AM 段距离 C、D 两加油站都越来越近,在 MN 段距离加油站 D 越来越近,而加油站 C 却越来越远.
A
B
C
D
M
N
10. 如图所示,火车站、码头分别位于A,B 两点,直线 a和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
解:如图所示:
(1)沿AB 走,两点之间线段最短;
(2)沿 BD 走,垂线段最短;
(3)沿 AC 走,垂线段最短.
火车站
码头
河流
铁路
1. 垂线的画法
2. 垂线的性质
(1) 在同一平面内,过一点有且只有一条直线与已知直线垂直;
(2) 垂线段最短.
3. 点到直线的距离
1. 习题4.5中第6、7、8题.
2.完成同步练习册中本课时的练习.
4.5 垂 线
第2课时 垂线段与点到直线的距离
1.掌握点到直线的距离的有关概念.
2.会作出直线外一点到一条直线的垂线.
3.理解垂线段最短的性质.
4.经过观察、分析、抽象、概括、画图等数学活动过程,进一步发展思维能力.
5.体会数学的应用价值.
【教学重点】
点到直线的距离的概念及垂线段最短的性质.
【教学难点】
垂线段最短的性质及从直线外一点作直线的垂线的画法.
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1. 垂线的定义
2. 垂线的性质
在同一平面内,垂直于同一条直线的两直线平行.
在同一平面内,如果一直线垂直于两条平行线中的一条,那么这条直线必垂直于另一条直线.
在灌溉时,要把河中的水引到农田 P 处,如何挖掘能使渠道最短?
河
课本P98“做一做”:(黑板上示范)
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点P画l的垂线,这样的垂线能画几条
(3)过直线l外的一点P画l的垂线,这样的垂线能画几条
.
l
.
(1)画已知直线 l 的垂线,这样的垂线能画出几条?
可以画无数条
(2) 经过直线 l 上一点 P 画 l 的垂线 a,这样的垂线能画几条?
可以画一条
(3)经过直线 l 外的一点 P 画 l 的垂线,这样的垂线能画几条?
可以画一条
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
3.过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
1、如图,设PO垂直于直线l,O为垂足,线段PO叫作P点到直线l 的垂线段.
P
B
l
O
A
C
2、通过P点的其他直线交 l 于A、B、
C…,线段PA,PB,PC都不是垂线段,称为斜线段.
垂线与垂线段有何区别和联系?
区别:垂线是直线,垂线段是线段.
联系:垂线和垂线段都有垂直关系.
1. 线段 AB,AC,AD ,AE 谁最短?
2.你能用一句话表示这个结论吗?
说一说:
如图,从 A 点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
C
D
E
B
l
A
直线外一点与直线上各点连接的所有线段中,垂线段最短. 简单说成:垂线段最短.
线段 AD 的长度叫做点 A 到直线 l 的距离.
特别规定:
D
l
A
在灌溉时,要把河中的水引到农田 P 处,如何挖掘能使渠道最短?请画出图来,并说明理由.
河
垂线段最短
【例3】如图,在三角形 ABC 中,∠ABC = 90°,BD⊥AC, 垂足为 D,AB = 5,BC = 12,AC = 13.
求:(1)点 A 到直线 BC 的距离;(2)点 B 到直线 AC 的距离.
解(1) 因为∠ABC = 90°,
所以 AB⊥BC, B为垂足.
所以线段 AB 即为点 A 到直线 BC 的垂线段.
因为AB = 5,
所以点 A 到直线 BC 的距离为 5.
(2)因为BD⊥AC
所以线段BD的长度点B到直线AC的距离.
所以点B到直线AC的距离为 .
如图,三角形 ABC 中,∠C=90°.
(1)分别指出点 A 到直线 BC,
点 B 到直线 AC 的距离是哪些
线段的长;
(2)三条边 AB、AC、BC 中
哪条边最长?为什么?
AC
BC
理由:连接直线外一点与直线上各点的所有线段中,垂线段最短.
AB.
1.如图,
①过点 Q 作 QD⊥AB,垂足为 D,
②过点 P 作 PE⊥AB,垂足为 E,
③过点 Q 作 QF⊥AC,垂足为 F,
④连 P、Q 两点,
⑤ P、Q 两点间的距离是线段______的长度,
⑥点 Q 到直线 AB 的距离是线段_______的长度,
⑦点 Q 到直线 AC 的距离是线段_______的长度,
⑧点 P 到直线 AB 的距离是线段________的长度.
解:①②③④ 作图如图所示
PQ
QD
QF
PE
2. 过点 P 向线段 AB 所在直线引垂线,正确的是( )
A B C D
C
3.如图,已知AC⊥BC于点C,CD⊥AB于点D,亮亮总结出了如下结论:
①线段AC的长,表示点A到直线BC的距离;
②线段CD的长,表示点C到直线AB的距离;
③线段AD的长,表示点A到直线CD的距离;
④∠ACD是∠BCD的余角.
亮亮总结的结论正确的有( )个.
A.1 B.2 C.3 D.4
C
4. 如图,AC⊥BC,∠CDB = 90°,线段 AC、BC、CD 中最短的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
5. P 是直线 AB 外一点,过点 P 作 PO⊥AB,垂足为 O,若 C 为直线 AB 上任意一点,则线段 PC 与线段 PO 的大小关系是( )
A. PC > PO B. PC < PO
C. PC ≥ PO D. PC ≥ PO
C
6. 如图,∠C = 90°,AB = 5,AC = 4,BC = 3,则点 A 到直线 BC 的距离为_____,点 B 到直线 AC 的距离为______,A、B 间的距离为______.
4
3
5
7. 下列说法正确的是( )
A. 线段 AB 叫做点 B 到直线 AC 的距离
B. 线段 AB 的长度叫做点 A 到直线 AC 的距离
C. 线段 BD 的长度叫做点 D 到直线 BC 的距离
D. 线段 BD 的长度叫做点 B 到直线 AC 的距离
A
B
C
D
D
8. 如图,在直角三角形 ABC 中,∠A = 90 °,AB = 3 cm,AC = 4 cm,BC = 5 cm,求点 A 到 BC 的距离,点 C 到 AB 的距离.
解: 点 A 到 BC 的距离是 cm.
点 C 到 AB 的距离是 4 cm.
9. 一辆汽车在直线形的公路 AB 上由 A 向 B 行驶,C、D 是分别位于公路 AB 两侧的加油站.
(1)设汽车行驶到公路 AB 上点 M 的位置时,距离加油站 C 最近;行驶到点 N 的位置时,距离加油站 D 最近,请在图中分别画出点 M、N 的位置;
A
B
C
D
M
N
(2)当汽车从 A 出发向 B 行驶时,在公路 AB 的哪一段路上距离 C、D 两加油站都越来越近?在哪一段路上距离加油站 D 越来越近,而离加油站 C 却越来越远?
解:在公路 AB 的 AM 段距离 C、D 两加油站都越来越近,在 MN 段距离加油站 D 越来越近,而加油站 C 却越来越远.
A
B
C
D
M
N
10. 如图所示,火车站、码头分别位于A,B 两点,直线 a和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
解:如图所示:
(1)沿AB 走,两点之间线段最短;
(2)沿 BD 走,垂线段最短;
(3)沿 AC 走,垂线段最短.
火车站
码头
河流
铁路
1. 垂线的画法
2. 垂线的性质
(1) 在同一平面内,过一点有且只有一条直线与已知直线垂直;
(2) 垂线段最短.
3. 点到直线的距离
1. 习题4.5中第6、7、8题.
2.完成同步练习册中本课时的练习.
