2023-2024学年人教版六年级下册数学第三单元圆柱与圆锥单元测试(无答案)
文档属性
| 名称 | 2023-2024学年人教版六年级下册数学第三单元圆柱与圆锥单元测试(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 18:29:22 | ||
图片预览

文档简介
人教版六年级下册数学第三单元练习10
(考试范围:第三单元)
一、我会填。(每空1分,共21分)
1.沿着圆柱的高剪开,侧面展开后得到一个( ),它的一条边长就等于圆柱的( ),另一条边长就等于圆柱的( )。
2.6000 毫升=( )升 3060立方厘米=( )立方分米
2.8立方米=( )立方分米 5平方米 40平方分米=( )平方米
3.用一张长6分米,宽5 分米的长方形铁皮制成一个圆柱,这个圆柱的侧面积最多是( )平方分米。 (接口处不计)
4.一个圆柱形储物盒的侧面积是 12.56 平方厘米,底面半径是 2 厘米,它的高是( )。
5.填一填,比一比。
(1)一个圆柱的体积是 1.8 立方分米,与它等底等高的圆锥的体积是( )立方分米。
(2)一个圆锥的体积是 1.8立方分米,与它等底等高的圆柱的体积是( )立方分米。
6.一个圆柱和一个圆锥等底等高,如果圆锥的体积比圆柱的体积少0.8立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米。
7.把一个棱长为 6 厘米的正方体木块削成一个最大的圆柱,削去部分的体积是( )立方厘米。
8.一个圆柱的表面积是 226.08 平方厘米,底面半径是 4 厘米,它们的侧面积是( )。
9.把一根长3 米的圆柱形木头截成三段,表面积增加 48 平方分米,这根圆柱形木头原来的体积是( )立方分米。
10.一个圆柱形罐头盒,高 1 分米,底面周长是 6.28 分米,罐头盒的侧面商标纸的面积最大是( )平方分米,这个罐头盒至少要用( )平方分米的铁皮。
11.把一根长 4 米,横截面半径为 2 分米的圆柱形木料截成同样长的5 段,表面积比原来增加( )平方分米。
12.一个圆柱的侧面积是56.52平方厘米,底面半径是 1.5 厘米,它的高是( )厘米,体积是( )。
二、判断。(对的画“√”,错的画“×”)(每题2分,共10分)
1.两个圆柱的底面积相等,那么它们的侧面积也一定相等。
2.表面积相等的两个圆柱,它们的体积也一定相等。
3.圆锥的侧面展开图是三角形。
4.长方体、正方体、圆锥的体积都可以用底面积乘高来计算。
5.一个底面内直径是 14 cm、高是 20cm的圆柱形杯子,能装下 3000 mL 的牛奶。
三、相信自己的选择。(每题2分,共10分)
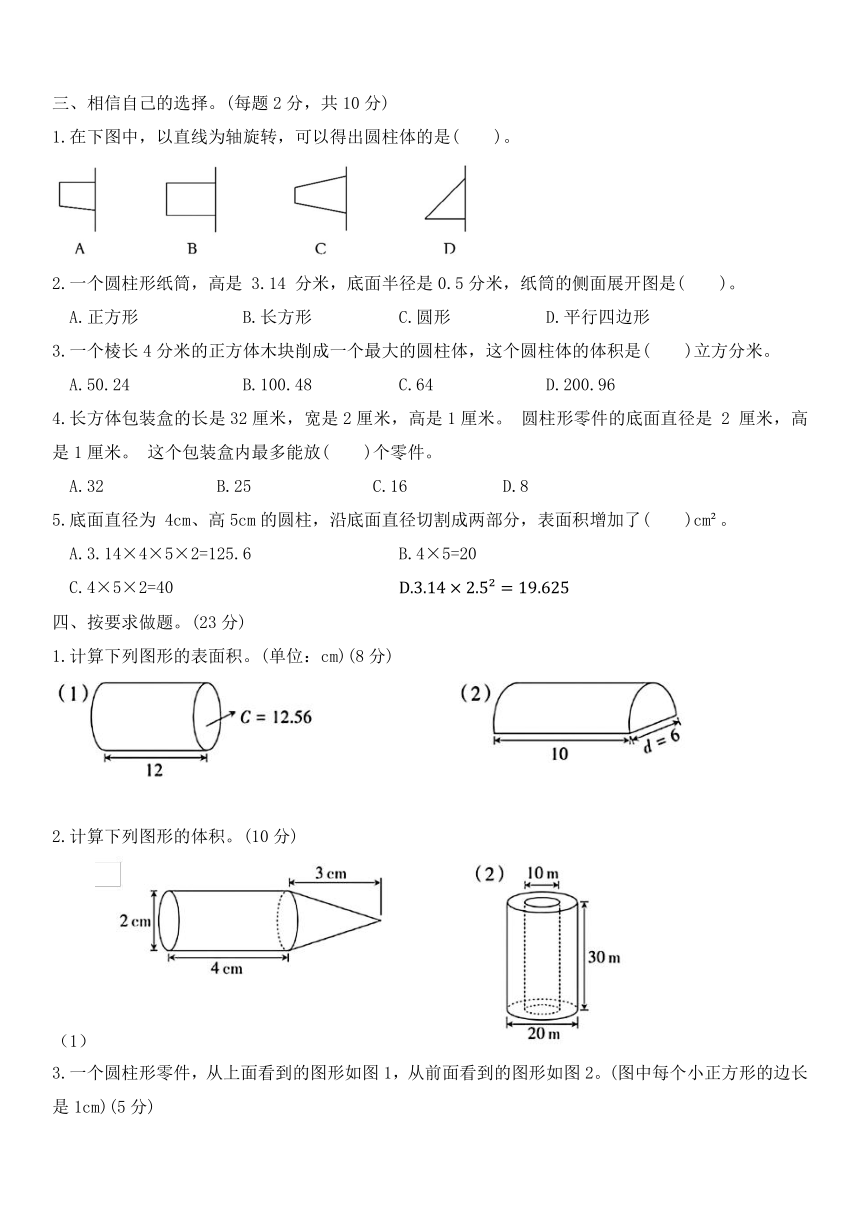
1.在下图中,以直线为轴旋转,可以得出圆柱体的是( )。
2.一个圆柱形纸筒,高是 3.14 分米,底面半径是0.5分米,纸筒的侧面展开图是( )。
A.正方形 B.长方形 C.圆形 D.平行四边形
3.一个棱长4分米的正方体木块削成一个最大的圆柱体,这个圆柱体的体积是( )立方分米。
A.50.24 B.100.48 C.64 D.200.96
4.长方体包装盒的长是32厘米,宽是2厘米,高是1厘米。 圆柱形零件的底面直径是 2 厘米,高是1厘米。 这个包装盒内最多能放( )个零件。
A.32 B.25 C.16 D.8
5.底面直径为 4cm、高5cm的圆柱,沿底面直径切割成两部分,表面积增加了( )cm 。
A.3.14×4×5×2=125.6 B.4×5=20
C.4×5×2=40
四、按要求做题。(23分)
1.计算下列图形的表面积。(单位:cm)(8分)
2.计算下列图形的体积。(10分)
(1)
3.一个圆柱形零件,从上面看到的图形如图1,从前面看到的图形如图2。(图中每个小正方形的边长是1cm)(5分)
(1)这个圆柱形零件的底面直径是( )厘米,高是( )厘米。(2分)
(2)这个零件的体积是多少立方厘米 (3分)
五、解决问题。(36分)
1.鼓的侧面是由铝皮围成的,上、下底面是羊皮。做这样一面鼓,至少需要多少平方米的铝皮 (结果保留整数)(5分)
2.一台压路机的滚筒宽5m,直径为1.8 m。如果它滚动20 周,压路的面积是多少平方米 (6分)
3.一个圆柱形钢管长3米,外直径是6分米,管壁的厚度是1分米,每立方分米的钢重7.8千克,20 根这样的钢管共重多少千克 (6分)
4.有一个油桶,底面直径是6分米,高是12分米,如果在油桶的表面刷上油漆,每平方米需要油漆500克,刷这个油桶需要多少克油漆 这个油桶大约能装多少升的油 (油桶的厚度忽略不计)(6分)
5.如右图所示,玻璃容器的底面直径为12cm,它的里面装有一部分水,水中浸没着一个高9 cm的圆锥形铅锤,当铅锤从水中取出后,水面下降了0.5cm,这个铅锤的底面积是多少 (6分)
6.一块圆柱形木料按图甲中的方式切成形状、大小相同的四块,表面积增加了;按图乙中的方式切成形状、大小相同的三块,表面积增加了若把它削成一个最大的圆锥,体积减小多少立方厘米 (7分)
(考试范围:第三单元)
一、我会填。(每空1分,共21分)
1.沿着圆柱的高剪开,侧面展开后得到一个( ),它的一条边长就等于圆柱的( ),另一条边长就等于圆柱的( )。
2.6000 毫升=( )升 3060立方厘米=( )立方分米
2.8立方米=( )立方分米 5平方米 40平方分米=( )平方米
3.用一张长6分米,宽5 分米的长方形铁皮制成一个圆柱,这个圆柱的侧面积最多是( )平方分米。 (接口处不计)
4.一个圆柱形储物盒的侧面积是 12.56 平方厘米,底面半径是 2 厘米,它的高是( )。
5.填一填,比一比。
(1)一个圆柱的体积是 1.8 立方分米,与它等底等高的圆锥的体积是( )立方分米。
(2)一个圆锥的体积是 1.8立方分米,与它等底等高的圆柱的体积是( )立方分米。
6.一个圆柱和一个圆锥等底等高,如果圆锥的体积比圆柱的体积少0.8立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米。
7.把一个棱长为 6 厘米的正方体木块削成一个最大的圆柱,削去部分的体积是( )立方厘米。
8.一个圆柱的表面积是 226.08 平方厘米,底面半径是 4 厘米,它们的侧面积是( )。
9.把一根长3 米的圆柱形木头截成三段,表面积增加 48 平方分米,这根圆柱形木头原来的体积是( )立方分米。
10.一个圆柱形罐头盒,高 1 分米,底面周长是 6.28 分米,罐头盒的侧面商标纸的面积最大是( )平方分米,这个罐头盒至少要用( )平方分米的铁皮。
11.把一根长 4 米,横截面半径为 2 分米的圆柱形木料截成同样长的5 段,表面积比原来增加( )平方分米。
12.一个圆柱的侧面积是56.52平方厘米,底面半径是 1.5 厘米,它的高是( )厘米,体积是( )。
二、判断。(对的画“√”,错的画“×”)(每题2分,共10分)
1.两个圆柱的底面积相等,那么它们的侧面积也一定相等。
2.表面积相等的两个圆柱,它们的体积也一定相等。
3.圆锥的侧面展开图是三角形。
4.长方体、正方体、圆锥的体积都可以用底面积乘高来计算。
5.一个底面内直径是 14 cm、高是 20cm的圆柱形杯子,能装下 3000 mL 的牛奶。
三、相信自己的选择。(每题2分,共10分)
1.在下图中,以直线为轴旋转,可以得出圆柱体的是( )。
2.一个圆柱形纸筒,高是 3.14 分米,底面半径是0.5分米,纸筒的侧面展开图是( )。
A.正方形 B.长方形 C.圆形 D.平行四边形
3.一个棱长4分米的正方体木块削成一个最大的圆柱体,这个圆柱体的体积是( )立方分米。
A.50.24 B.100.48 C.64 D.200.96
4.长方体包装盒的长是32厘米,宽是2厘米,高是1厘米。 圆柱形零件的底面直径是 2 厘米,高是1厘米。 这个包装盒内最多能放( )个零件。
A.32 B.25 C.16 D.8
5.底面直径为 4cm、高5cm的圆柱,沿底面直径切割成两部分,表面积增加了( )cm 。
A.3.14×4×5×2=125.6 B.4×5=20
C.4×5×2=40
四、按要求做题。(23分)
1.计算下列图形的表面积。(单位:cm)(8分)
2.计算下列图形的体积。(10分)
(1)
3.一个圆柱形零件,从上面看到的图形如图1,从前面看到的图形如图2。(图中每个小正方形的边长是1cm)(5分)
(1)这个圆柱形零件的底面直径是( )厘米,高是( )厘米。(2分)
(2)这个零件的体积是多少立方厘米 (3分)
五、解决问题。(36分)
1.鼓的侧面是由铝皮围成的,上、下底面是羊皮。做这样一面鼓,至少需要多少平方米的铝皮 (结果保留整数)(5分)
2.一台压路机的滚筒宽5m,直径为1.8 m。如果它滚动20 周,压路的面积是多少平方米 (6分)
3.一个圆柱形钢管长3米,外直径是6分米,管壁的厚度是1分米,每立方分米的钢重7.8千克,20 根这样的钢管共重多少千克 (6分)
4.有一个油桶,底面直径是6分米,高是12分米,如果在油桶的表面刷上油漆,每平方米需要油漆500克,刷这个油桶需要多少克油漆 这个油桶大约能装多少升的油 (油桶的厚度忽略不计)(6分)
5.如右图所示,玻璃容器的底面直径为12cm,它的里面装有一部分水,水中浸没着一个高9 cm的圆锥形铅锤,当铅锤从水中取出后,水面下降了0.5cm,这个铅锤的底面积是多少 (6分)
6.一块圆柱形木料按图甲中的方式切成形状、大小相同的四块,表面积增加了;按图乙中的方式切成形状、大小相同的三块,表面积增加了若把它削成一个最大的圆锥,体积减小多少立方厘米 (7分)
