2024年河南省中考数学复习模拟试卷(八)(含答案)
文档属性
| 名称 | 2024年河南省中考数学复习模拟试卷(八)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 841.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 22:40:09 | ||
图片预览




文档简介
2024年河南省中考数学复习模拟试卷(八)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.下列各组数中,不相等的是( )
A.(﹣3)2与32 B.(﹣2)3与﹣23
C.|﹣2|3与|﹣23| D.(﹣3)2与﹣32
2.下面四个立体图形中,俯视图是三角形的是( )
A. B.
C. D.
3.根据国家统计局最新数据,2019年1至2月份全国房地产开发投资12000亿元,同比增长11.6%.数12000用科学记数法表示为( )
A.1.2×103 B.12×103 C.1.2×104 D.0.12×105
4.如图,把一张长方形的纸片沿着EF折叠,点C、D分别落在M、N的位置,且∠MFB= ∠MFE.则∠EFM的度数为( )
A.30° B.36° C.45° D.72°
5.计算 的结果为( )
A. B.1 C. D.2
6.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.360° C.540° D.720°
7.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A. B. C. D.
8.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中摸出一个小球,再从余下的球中摸出一个小球,第二次摸到小球的编号大于第一次编号的概率是( )
A. B. C. D.
9.在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
A. B. C. D.
10.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( ).
A.4 B.6 C.8 D.10
二、填空题(每小题3分,共15分)
11.有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是 .
12.要使 有意义,则x的取值范围是 .
13.我国是世界上验证缺水的国家之一,全国总用水量逐年上升,全国总用水量可分为农业用水量、工业用水量和生活用水量三部分.为了合理利用水资源,我国连续多年对水资源的利用情况进行跟踪调查,将所得数据进行处理,绘制了2014年全国总用水量分布情况扇形统计图和2010~2014年全国生活用水量折线统计图的一部分如下:
(1)2013年全国生活用水量比2010年增加了16%,则2010年全国生活用水量为 亿m3,2014年全国生活用水量比2010年增加了20%,则2014年全国生活用水量为 亿m3;
(2)根据以上信息,2014年全国总用水量为 亿m3.
14.如图..在等腰△ABC中,AB=AC=5, BC=6, AD⊥BC, CE⊥AB,则EC= .
15.将一张宽度相等的长方形纸条按如图所示的方式折叠一下,如果∠1=140°,那么∠2的度数是 .
三、解答题(本大题共8个小题,共75分)
16.
(1)计算: ;
(2)计算: .
17.为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 频数
1.2≤x<1.6 a
1.6≤x<2.0 12
2.0≤x<2.4 b
2.4≤x<2.8 10
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有850名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
18.如图,在△ABC中,,∠B=60°,∠C=45°.
(1)用尺规作图的方法作出∠B的角平分线;(保留作图痕迹,不写作法)
(2)若(1)中的角平分线交AC于点D,求△BDC的面积.
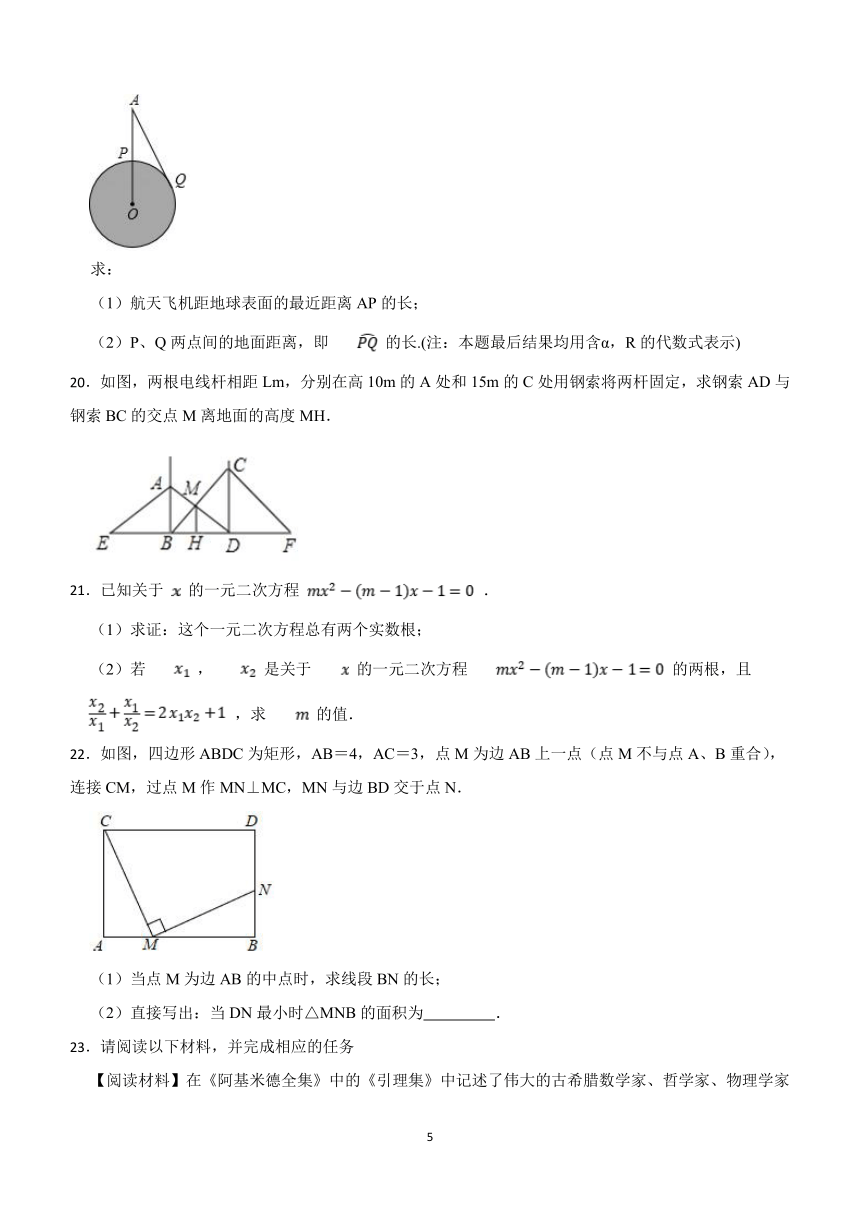
19.如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,即AQ是⊙O的切线,若∠QAP=α,地球半径为R,
求:
(1)航天飞机距地球表面的最近距离AP的长;
(2)P、Q两点间的地面距离,即 的长.(注:本题最后结果均用含α,R的代数式表示)
20.如图,两根电线杆相距Lm,分别在高10m的A处和15m的C处用钢索将两杆固定,求钢索AD与钢索BC的交点M离地面的高度MH.
21.已知关于 的一元二次方程 .
(1)求证:这个一元二次方程总有两个实数根;
(2)若 , 是关于 的一元二次方程 的两根,且 ,求 的值.
22.如图,四边形ABDC为矩形,AB=4,AC=3,点M为边AB上一点(点M不与点A、B重合),连接CM,过点M作MN⊥MC,MN与边BD交于点N.
(1)当点M为边AB的中点时,求线段BN的长;
(2)直接写出:当DN最小时△MNB的面积为 .
23.请阅读以下材料,并完成相应的任务
【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:
如图1,点P是弧的任意一点,于点C,点D在弦上且,在弧上取一点Q,使弧=弧,连接,则有.
(1)如图2,小明同学尝试说明“”,于是他连接了,,,,请根据小明的思路完成后续证明过程;
(2)如图3,以为直径的半圆上有一点P,,直线l与相切于点P,过点于点E,交于点Q,求出的长.
答案解析
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】A
10.【答案】C
11.【答案】25°或40°或10°
12.【答案】
13.【答案】625;750;5000
14.【答案】4.8
15.【答案】110°
16.【答案】(1)解:原式=
= ;
(2)解:原式=
=
= .
17.【答案】(1)8;20;2.0≤x<2.4
(2)解:由(1)知,b=20,
补全的频数分布直方图如图所示;
(3)170(人)
解:850× =170(人).
答:该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有170人。
18.【答案】(1)解:如图,射线即为所作.
(2)解:如图,过点D作于点F,
,
是等腰直角三角形,且,
设,
平分,且,
,
,,
,
,
解得,
即,
则的面积为.
19.【答案】(1)解:由题意,从A处观测到地球上的最远点Q,
∴AQ是⊙O的切线,切点为Q,
连接OQ,则OQ垂直于AQ,如图,
则在直角△OAQ中有 =sinα,
即AP= ﹣R;
(2)解:在直角△OAQ中,
则∠O=90°﹣α,
由弧长公式得 的长= .
20.【答案】解:∵AB∥CD,
∴△ABM∽△DCM,
∴
设BH=2x,则DH=3x,
∵MH∥AB,
∴△MDH∽△ADB,
∴
∴MH=AB=6.
答:钢索AD与钢索BC的交点M离地面的高度MH为6m.
21.【答案】(1)解:由题意得, 即 故这个一元二次方程总有连个实数根
(2)解:
整理得, 解得 或
22.【答案】(1)解:∵AB=4,
∴当点M为边AB的中点时,AM=BM=2,
∵四边形ABDC为矩形,
∴∠A=∠B=90°,
∵MN⊥MC,
∴∠CMN=90°,
∵∠ACM+∠AMC=90°,∠BMN+∠AMC=180°﹣∠CMN=90°,
∴∠ACM=∠BMN,
又∵∠A=∠B,
∴△ACM∽△BMN,
∴ ,
∵AC=3,AM=BM=2,
∴ ,
∴BN=
(2)
23.【答案】(1)证明:∵于点C, ,
∴是的垂直平分线,
∴,
∴,
∵,
∴,
又∵,
∴,
∴;
(2)解:如图,连接,
∵为直径,
∴,
∵,
∴,
∵,
∴,
∵直线l与相切于点P,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴.
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.下列各组数中,不相等的是( )
A.(﹣3)2与32 B.(﹣2)3与﹣23
C.|﹣2|3与|﹣23| D.(﹣3)2与﹣32
2.下面四个立体图形中,俯视图是三角形的是( )
A. B.
C. D.
3.根据国家统计局最新数据,2019年1至2月份全国房地产开发投资12000亿元,同比增长11.6%.数12000用科学记数法表示为( )
A.1.2×103 B.12×103 C.1.2×104 D.0.12×105
4.如图,把一张长方形的纸片沿着EF折叠,点C、D分别落在M、N的位置,且∠MFB= ∠MFE.则∠EFM的度数为( )
A.30° B.36° C.45° D.72°
5.计算 的结果为( )
A. B.1 C. D.2
6.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.360° C.540° D.720°
7.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A. B. C. D.
8.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中摸出一个小球,再从余下的球中摸出一个小球,第二次摸到小球的编号大于第一次编号的概率是( )
A. B. C. D.
9.在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
A. B. C. D.
10.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( ).
A.4 B.6 C.8 D.10
二、填空题(每小题3分,共15分)
11.有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是 .
12.要使 有意义,则x的取值范围是 .
13.我国是世界上验证缺水的国家之一,全国总用水量逐年上升,全国总用水量可分为农业用水量、工业用水量和生活用水量三部分.为了合理利用水资源,我国连续多年对水资源的利用情况进行跟踪调查,将所得数据进行处理,绘制了2014年全国总用水量分布情况扇形统计图和2010~2014年全国生活用水量折线统计图的一部分如下:
(1)2013年全国生活用水量比2010年增加了16%,则2010年全国生活用水量为 亿m3,2014年全国生活用水量比2010年增加了20%,则2014年全国生活用水量为 亿m3;
(2)根据以上信息,2014年全国总用水量为 亿m3.
14.如图..在等腰△ABC中,AB=AC=5, BC=6, AD⊥BC, CE⊥AB,则EC= .
15.将一张宽度相等的长方形纸条按如图所示的方式折叠一下,如果∠1=140°,那么∠2的度数是 .
三、解答题(本大题共8个小题,共75分)
16.
(1)计算: ;
(2)计算: .
17.为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 频数
1.2≤x<1.6 a
1.6≤x<2.0 12
2.0≤x<2.4 b
2.4≤x<2.8 10
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有850名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
18.如图,在△ABC中,,∠B=60°,∠C=45°.
(1)用尺规作图的方法作出∠B的角平分线;(保留作图痕迹,不写作法)
(2)若(1)中的角平分线交AC于点D,求△BDC的面积.
19.如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,即AQ是⊙O的切线,若∠QAP=α,地球半径为R,
求:
(1)航天飞机距地球表面的最近距离AP的长;
(2)P、Q两点间的地面距离,即 的长.(注:本题最后结果均用含α,R的代数式表示)
20.如图,两根电线杆相距Lm,分别在高10m的A处和15m的C处用钢索将两杆固定,求钢索AD与钢索BC的交点M离地面的高度MH.
21.已知关于 的一元二次方程 .
(1)求证:这个一元二次方程总有两个实数根;
(2)若 , 是关于 的一元二次方程 的两根,且 ,求 的值.
22.如图,四边形ABDC为矩形,AB=4,AC=3,点M为边AB上一点(点M不与点A、B重合),连接CM,过点M作MN⊥MC,MN与边BD交于点N.
(1)当点M为边AB的中点时,求线段BN的长;
(2)直接写出:当DN最小时△MNB的面积为 .
23.请阅读以下材料,并完成相应的任务
【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:
如图1,点P是弧的任意一点,于点C,点D在弦上且,在弧上取一点Q,使弧=弧,连接,则有.
(1)如图2,小明同学尝试说明“”,于是他连接了,,,,请根据小明的思路完成后续证明过程;
(2)如图3,以为直径的半圆上有一点P,,直线l与相切于点P,过点于点E,交于点Q,求出的长.
答案解析
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】A
10.【答案】C
11.【答案】25°或40°或10°
12.【答案】
13.【答案】625;750;5000
14.【答案】4.8
15.【答案】110°
16.【答案】(1)解:原式=
= ;
(2)解:原式=
=
= .
17.【答案】(1)8;20;2.0≤x<2.4
(2)解:由(1)知,b=20,
补全的频数分布直方图如图所示;
(3)170(人)
解:850× =170(人).
答:该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有170人。
18.【答案】(1)解:如图,射线即为所作.
(2)解:如图,过点D作于点F,
,
是等腰直角三角形,且,
设,
平分,且,
,
,,
,
,
解得,
即,
则的面积为.
19.【答案】(1)解:由题意,从A处观测到地球上的最远点Q,
∴AQ是⊙O的切线,切点为Q,
连接OQ,则OQ垂直于AQ,如图,
则在直角△OAQ中有 =sinα,
即AP= ﹣R;
(2)解:在直角△OAQ中,
则∠O=90°﹣α,
由弧长公式得 的长= .
20.【答案】解:∵AB∥CD,
∴△ABM∽△DCM,
∴
设BH=2x,则DH=3x,
∵MH∥AB,
∴△MDH∽△ADB,
∴
∴MH=AB=6.
答:钢索AD与钢索BC的交点M离地面的高度MH为6m.
21.【答案】(1)解:由题意得, 即 故这个一元二次方程总有连个实数根
(2)解:
整理得, 解得 或
22.【答案】(1)解:∵AB=4,
∴当点M为边AB的中点时,AM=BM=2,
∵四边形ABDC为矩形,
∴∠A=∠B=90°,
∵MN⊥MC,
∴∠CMN=90°,
∵∠ACM+∠AMC=90°,∠BMN+∠AMC=180°﹣∠CMN=90°,
∴∠ACM=∠BMN,
又∵∠A=∠B,
∴△ACM∽△BMN,
∴ ,
∵AC=3,AM=BM=2,
∴ ,
∴BN=
(2)
23.【答案】(1)证明:∵于点C, ,
∴是的垂直平分线,
∴,
∴,
∵,
∴,
又∵,
∴,
∴;
(2)解:如图,连接,
∵为直径,
∴,
∵,
∴,
∵,
∴,
∵直线l与相切于点P,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴.
同课章节目录
