2024年河南省中考数学复习模拟试卷(五)(含答案)
文档属性
| 名称 | 2024年河南省中考数学复习模拟试卷(五)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 922.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 22:46:54 | ||
图片预览

文档简介
2024年河南省中考数学复习模拟试卷(五)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.a,b是有理数,它们在数轴上的对应点的位置如图所示,对于以下结论,正确的是( )
A. B. C. D.
2.在下面的四个几何体中,左视图与主视图不相同的几何体是( )
A.正方体 B.圆柱
C.直三棱柱 D.圆锥
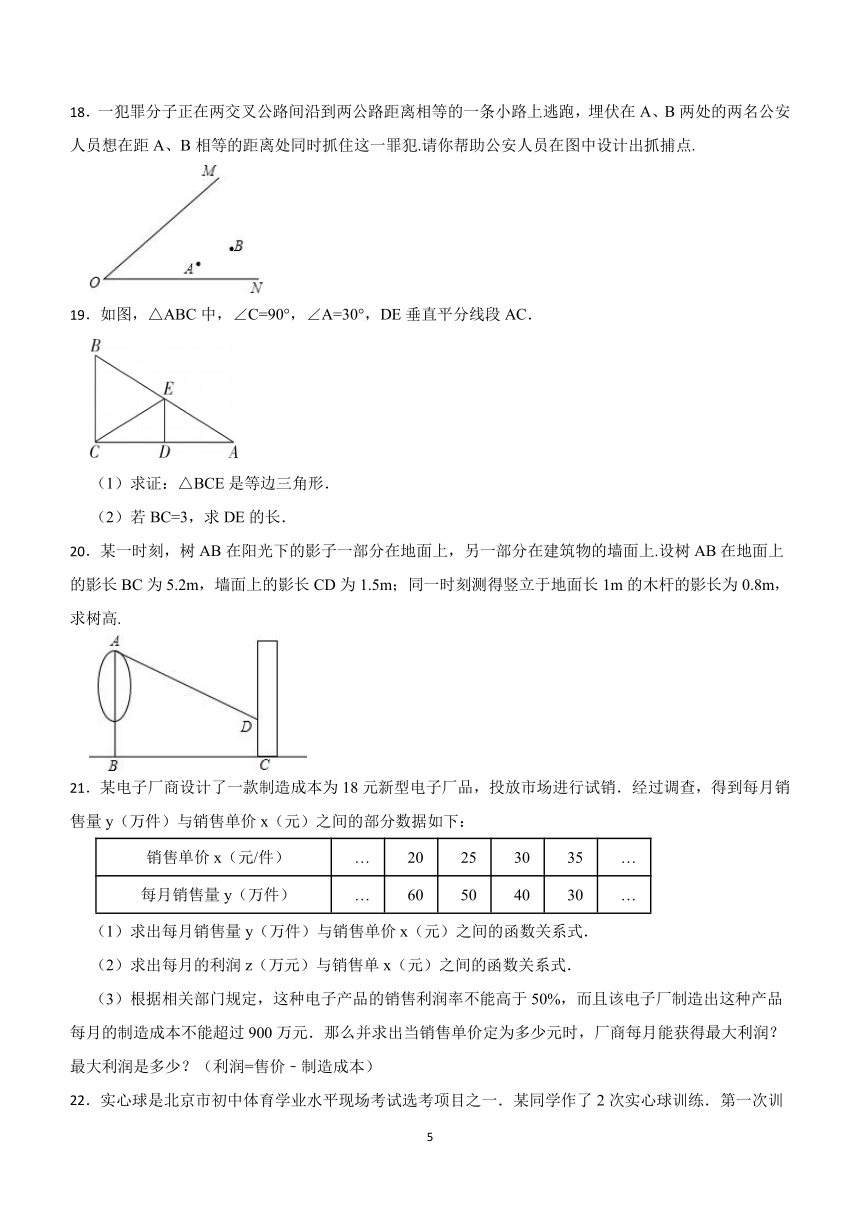
3.江苏省的面积约为102 600 km2,102600这个数据用科学记数法可表示为( )
A. B. C. D.
4.用矩形纸片折出直角的平分线,下列折法正确的是( )
A. B.
C. D.
5.下列运算正确的是( )
A. B.
C. D.
6.如图,在△ABC中, AB=AC,AB的垂直平分线DE交AC于E.若∠A=40°,则∠EBC的度数是( )
A.30° B.35° C.40° D.45°
7.如图是一纸条的示意图,第1次对折,使A,B两点重合后再打开,折痕为l1;第2次对折,使A,C两点重合后再打开,折痕为l2;第3次对折,使B,D两点重合后再打开,折痕为l3.已知CE=2cm,则纸条原长为( )cm
A.18 B.16 C.14 D.12
8.在a2□4a□4的空格中,任意填上“+”或“-”,在所得到的代数式中,可以构成完全平方式的概率是( )
A. B. C. D.1
9.已知二次函数 的图象如下,则一次函数 与反比例函数 在同一平面直角坐标系中的图象大致是( )
A. B.
C. D.
10.如图,边长为2的菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,CF的值为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.如图,四边形ABCD中,AC=BC=BD,且AC⊥BD,若AB=a,则△ABD的面积为 .(用含a的式子表示)
12.已知关于x、y的二元一次方程组的解满足x+y=0,则m的值为
13.某中学共40位同学参加了演讲比赛,分段统计参赛同学的成绩,结果如下(分数为整数,满分为100分)
分数段(分〕 61~70 71~80 81~90 91~100
人数 5 10 16
则m= ;若制作成扇形统计图,那么81~90分数段所对应扇形的圆心角为 °.
14.如图,在长方形纸片 中, , ,拆叠纸片 ,使顶点C落在边 上的点G处,折痕分别交边 、 于点E、F ,则 的面积最大值是 .
15.如图、在菱形ABCD中,∠ADC=128°,P是对角线AC,BD的交点,点E在CB的延长线上,且PE=PA.则∠APE= 度。
三、解答题(本大题共8个小题,共75分)
16.计算:
(1) ;
(2) .
17.某初中要调查学校学生(总数 1000 人)双休日课外阅读情况,随机调查了一部分学生,调查得 到的数据分别制成频数直方图(如图 1)和扇形统计图(如图 2).
(1)请补全上述统计图(直接填在图中);
(2)试确定这个样本的中位数和众数;
(3)请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.
18.一犯罪分子正在两交叉公路间沿到两公路距离相等的一条小路上逃跑,埋伏在A、B两处的两名公安人员想在距A、B相等的距离处同时抓住这一罪犯.请你帮助公安人员在图中设计出抓捕点.
19.如图,△ABC中,∠C=90°,∠A=30°,DE垂直平分线段AC.
(1)求证:△BCE是等边三角形.
(2)若BC=3,求DE的长.
20.某一时刻,树AB在阳光下的影子一部分在地面上,另一部分在建筑物的墙面上.设树AB在地面上的影长BC为5.2m,墙面上的影长CD为1.5m;同一时刻测得竖立于地面长1m的木杆的影长为0.8m,求树高.
21.某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) … 20 25 30 35 …
每月销售量y(万件) … 60 50 40 30 …
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
22.实心球是北京市初中体育学业水平现场考试选考项目之一.某同学作了2次实心球训练.第一次训练中实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图所示,掷出时起点处高度为,当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数表达式;
(2)该同学第二次训练实心球的竖直高度y与水平距离x近似满足函数关系:,记第一次实心球从起点到落地点的水平距离为,第二次实心球从起点到落地点的水平距离为,则 .(填“>”“=”或“<”).
23.如图1, 中, 边上的中线 ,延长 交 的外接圆于点 ,过点 作DE BC交圆于点 ,延长 交 的延长线于点 ,连结 .
(1)【特殊尝试】若 , ,求 和 的长;
(2)【规律探索】
①求证: ;
②设 , ,求 关于 的函数表达式:
(3)【拓展应用】
如图2,作 交线段 于 ,连结 ,当 的面积是 面积的6倍时,求 的值.
答案解析
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】 a2
12.【答案】1
13.【答案】9;144
14.【答案】7.5
15.【答案】52
16.【答案】(1)
(2)
17.【答案】(1)解:总人数:6 12%= 50 (人),
阅读3小时以上人数:50-4-6-8-14-6= 12 (人),
阅读3小时以上人数的百分比为12 50= 24% ,
阅读0小时以上人数的百分比为4 50= 8% .
图如下:
(2)中位数是3小时,众数是4小时
(3)解:1000 (28% + 12%)
= 1000 40%
= 400(人)
答:该学校1000名学生双休日课外阅读时间不少于4小时的人数为400人.
18.【答案】解:角平分线上的点到角两边的距离相等(即犯罪分子在∠MON的角平分线上,点P也在其上)
线段垂直平分线上的点到线段两端点的距离相等(所以点P在线段AB的垂直平分线上).
∴两线的交点,即点P符合要求.
19.【答案】(1)证明:在△ABC中,
∵
∵DE垂直平分AC,
∴EC=EA,
∴
∴∠BEC=∠A+∠ECA=60° ,
∴△BCE是等边三角形;
(2)解:∵△BCE是等边三角形,
∴EC=BC=3,
Rt△ECD中,∵
∴.
20.【答案】解:过点D作DE⊥AB于点E,
∵AB⊥BC,DC⊥BC,
∴四边形BCDE是矩形,
∴BC=DE=5.2m,BE=CD=1.5m,
∵在同一时刻物高与影长成正比,
∴ = ,即 = ,解得
∴AE=6.5m,
∴AB=AE+EB=6.5+1.5=8m,
∴树的高度为8m.
答:树的高度为8m.
21.【答案】(1)解:设销售量y(万件)与销售单价x(元)之间的函数关系式为:y=kx+b,
把(20,60),(30,40)代入y=kx+b得 ,
解得: ,
∴每月销售量y(万件)与销售单价x(元)之间的函数关系式为:y=﹣2x+100
(2)解:由题意得,z=y(x﹣18)
=(﹣2x+100)(x﹣18)
=﹣2x2+136x﹣1800
(3)解:∵厂商每月的制造成本不超过900万元,每件制造成本为18元,
∴每月的生产量为:小于等于 =50万件,
y=﹣2x+100≤50,
解得:x≥25,
又由销售利润率不能高于50%,得25≤x≤27,
∵z=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴图象开口向下,对称轴左侧z随x的增大而增大,
∴x=27时,z最大为:404万元.
当销售单价为27元时,厂商每月获得的利润最大,最大利润为404万元
22.【答案】(1)解:根据题意设关于的函数表达式为,
把代入解析式得,,
解得,,
∴关于的函数表达式为
(2)<
23.【答案】(1)解:如图,连接 ,
, ,
.
又 ,
, 都是等边三角形.
,
,
.
,
.
(2)解:①如图,连接 , ,
,
,
,
.
由(1)得:
,
,
,
即BC=2CE.
②由上可得 ,
.
由(1)得 ,
如图,过点A作 于点H,
设 ,
,
.
,
则 ,
(3)解:如图,连接ME,
由上得 ,
,
, ,
,
.
,
.
.
.
面积是 面积的6倍,
面积是 面积的3倍.
.
设 交 于点K,
则 , ,
.
.
,
.
,
解得 .
即 .
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1.a,b是有理数,它们在数轴上的对应点的位置如图所示,对于以下结论,正确的是( )
A. B. C. D.
2.在下面的四个几何体中,左视图与主视图不相同的几何体是( )
A.正方体 B.圆柱
C.直三棱柱 D.圆锥
3.江苏省的面积约为102 600 km2,102600这个数据用科学记数法可表示为( )
A. B. C. D.
4.用矩形纸片折出直角的平分线,下列折法正确的是( )
A. B.
C. D.
5.下列运算正确的是( )
A. B.
C. D.
6.如图,在△ABC中, AB=AC,AB的垂直平分线DE交AC于E.若∠A=40°,则∠EBC的度数是( )
A.30° B.35° C.40° D.45°
7.如图是一纸条的示意图,第1次对折,使A,B两点重合后再打开,折痕为l1;第2次对折,使A,C两点重合后再打开,折痕为l2;第3次对折,使B,D两点重合后再打开,折痕为l3.已知CE=2cm,则纸条原长为( )cm
A.18 B.16 C.14 D.12
8.在a2□4a□4的空格中,任意填上“+”或“-”,在所得到的代数式中,可以构成完全平方式的概率是( )
A. B. C. D.1
9.已知二次函数 的图象如下,则一次函数 与反比例函数 在同一平面直角坐标系中的图象大致是( )
A. B.
C. D.
10.如图,边长为2的菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,CF的值为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.如图,四边形ABCD中,AC=BC=BD,且AC⊥BD,若AB=a,则△ABD的面积为 .(用含a的式子表示)
12.已知关于x、y的二元一次方程组的解满足x+y=0,则m的值为
13.某中学共40位同学参加了演讲比赛,分段统计参赛同学的成绩,结果如下(分数为整数,满分为100分)
分数段(分〕 61~70 71~80 81~90 91~100
人数 5 10 16
则m= ;若制作成扇形统计图,那么81~90分数段所对应扇形的圆心角为 °.
14.如图,在长方形纸片 中, , ,拆叠纸片 ,使顶点C落在边 上的点G处,折痕分别交边 、 于点E、F ,则 的面积最大值是 .
15.如图、在菱形ABCD中,∠ADC=128°,P是对角线AC,BD的交点,点E在CB的延长线上,且PE=PA.则∠APE= 度。
三、解答题(本大题共8个小题,共75分)
16.计算:
(1) ;
(2) .
17.某初中要调查学校学生(总数 1000 人)双休日课外阅读情况,随机调查了一部分学生,调查得 到的数据分别制成频数直方图(如图 1)和扇形统计图(如图 2).
(1)请补全上述统计图(直接填在图中);
(2)试确定这个样本的中位数和众数;
(3)请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.
18.一犯罪分子正在两交叉公路间沿到两公路距离相等的一条小路上逃跑,埋伏在A、B两处的两名公安人员想在距A、B相等的距离处同时抓住这一罪犯.请你帮助公安人员在图中设计出抓捕点.
19.如图,△ABC中,∠C=90°,∠A=30°,DE垂直平分线段AC.
(1)求证:△BCE是等边三角形.
(2)若BC=3,求DE的长.
20.某一时刻,树AB在阳光下的影子一部分在地面上,另一部分在建筑物的墙面上.设树AB在地面上的影长BC为5.2m,墙面上的影长CD为1.5m;同一时刻测得竖立于地面长1m的木杆的影长为0.8m,求树高.
21.某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) … 20 25 30 35 …
每月销售量y(万件) … 60 50 40 30 …
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
22.实心球是北京市初中体育学业水平现场考试选考项目之一.某同学作了2次实心球训练.第一次训练中实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图所示,掷出时起点处高度为,当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数表达式;
(2)该同学第二次训练实心球的竖直高度y与水平距离x近似满足函数关系:,记第一次实心球从起点到落地点的水平距离为,第二次实心球从起点到落地点的水平距离为,则 .(填“>”“=”或“<”).
23.如图1, 中, 边上的中线 ,延长 交 的外接圆于点 ,过点 作DE BC交圆于点 ,延长 交 的延长线于点 ,连结 .
(1)【特殊尝试】若 , ,求 和 的长;
(2)【规律探索】
①求证: ;
②设 , ,求 关于 的函数表达式:
(3)【拓展应用】
如图2,作 交线段 于 ,连结 ,当 的面积是 面积的6倍时,求 的值.
答案解析
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】 a2
12.【答案】1
13.【答案】9;144
14.【答案】7.5
15.【答案】52
16.【答案】(1)
(2)
17.【答案】(1)解:总人数:6 12%= 50 (人),
阅读3小时以上人数:50-4-6-8-14-6= 12 (人),
阅读3小时以上人数的百分比为12 50= 24% ,
阅读0小时以上人数的百分比为4 50= 8% .
图如下:
(2)中位数是3小时,众数是4小时
(3)解:1000 (28% + 12%)
= 1000 40%
= 400(人)
答:该学校1000名学生双休日课外阅读时间不少于4小时的人数为400人.
18.【答案】解:角平分线上的点到角两边的距离相等(即犯罪分子在∠MON的角平分线上,点P也在其上)
线段垂直平分线上的点到线段两端点的距离相等(所以点P在线段AB的垂直平分线上).
∴两线的交点,即点P符合要求.
19.【答案】(1)证明:在△ABC中,
∵
∵DE垂直平分AC,
∴EC=EA,
∴
∴∠BEC=∠A+∠ECA=60° ,
∴△BCE是等边三角形;
(2)解:∵△BCE是等边三角形,
∴EC=BC=3,
Rt△ECD中,∵
∴.
20.【答案】解:过点D作DE⊥AB于点E,
∵AB⊥BC,DC⊥BC,
∴四边形BCDE是矩形,
∴BC=DE=5.2m,BE=CD=1.5m,
∵在同一时刻物高与影长成正比,
∴ = ,即 = ,解得
∴AE=6.5m,
∴AB=AE+EB=6.5+1.5=8m,
∴树的高度为8m.
答:树的高度为8m.
21.【答案】(1)解:设销售量y(万件)与销售单价x(元)之间的函数关系式为:y=kx+b,
把(20,60),(30,40)代入y=kx+b得 ,
解得: ,
∴每月销售量y(万件)与销售单价x(元)之间的函数关系式为:y=﹣2x+100
(2)解:由题意得,z=y(x﹣18)
=(﹣2x+100)(x﹣18)
=﹣2x2+136x﹣1800
(3)解:∵厂商每月的制造成本不超过900万元,每件制造成本为18元,
∴每月的生产量为:小于等于 =50万件,
y=﹣2x+100≤50,
解得:x≥25,
又由销售利润率不能高于50%,得25≤x≤27,
∵z=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴图象开口向下,对称轴左侧z随x的增大而增大,
∴x=27时,z最大为:404万元.
当销售单价为27元时,厂商每月获得的利润最大,最大利润为404万元
22.【答案】(1)解:根据题意设关于的函数表达式为,
把代入解析式得,,
解得,,
∴关于的函数表达式为
(2)<
23.【答案】(1)解:如图,连接 ,
, ,
.
又 ,
, 都是等边三角形.
,
,
.
,
.
(2)解:①如图,连接 , ,
,
,
,
.
由(1)得:
,
,
,
即BC=2CE.
②由上可得 ,
.
由(1)得 ,
如图,过点A作 于点H,
设 ,
,
.
,
则 ,
(3)解:如图,连接ME,
由上得 ,
,
, ,
,
.
,
.
.
.
面积是 面积的6倍,
面积是 面积的3倍.
.
设 交 于点K,
则 , ,
.
.
,
.
,
解得 .
即 .
同课章节目录
