四年级下册数学北师大版5.4 方程(课件)(共30张PPT)
文档属性
| 名称 | 四年级下册数学北师大版5.4 方程(课件)(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 19:03:11 | ||
图片预览





文档简介
(共30张PPT)
北师版四年级数学下册
认识方程
第3节 方程
汇报人:XXX 时间:XXXXX
1.结合具体情境了解方程的意义,会用方程表示简单情境中的等量关系。
2.经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。
3.在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
4.理解方程的意义,会用方程表示简单情景中的等量关系。
5.找准实际问题中的等量关系。
学习目标
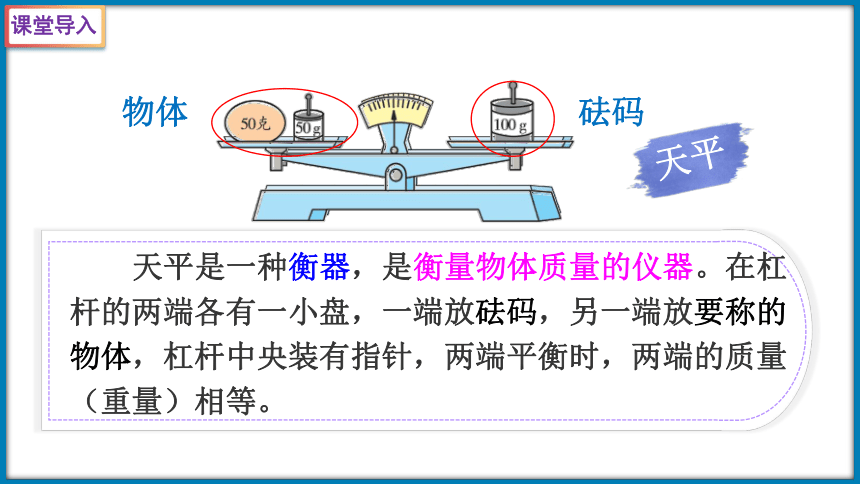
天平
天平是一种衡器,是衡量物体质量的仪器。在杠杆的两端各有一小盘,一端放砝码,另一端放要称的物体,杠杆中央装有指针,两端平衡时,两端的质量(重量)相等。
物体
砝码
课堂导入
观察天平上的指针,发现指针指向正中间,说明天平平衡。
物品
砝码
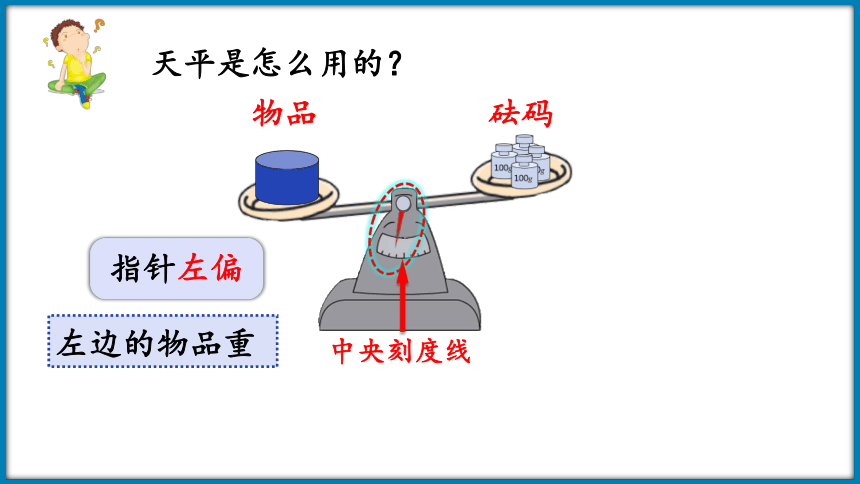
中央刻度线
天平是怎么用的?
天平平衡,说明左右两边物体的质量相等。
物品
砝码
中央刻度线
左边的物品重
指针左偏
天平是怎么用的?
物品
砝码
左边的物品重
指针左偏
右边的砝码重
指针右偏
中央刻度线
天平是怎么用的?
10g
2g
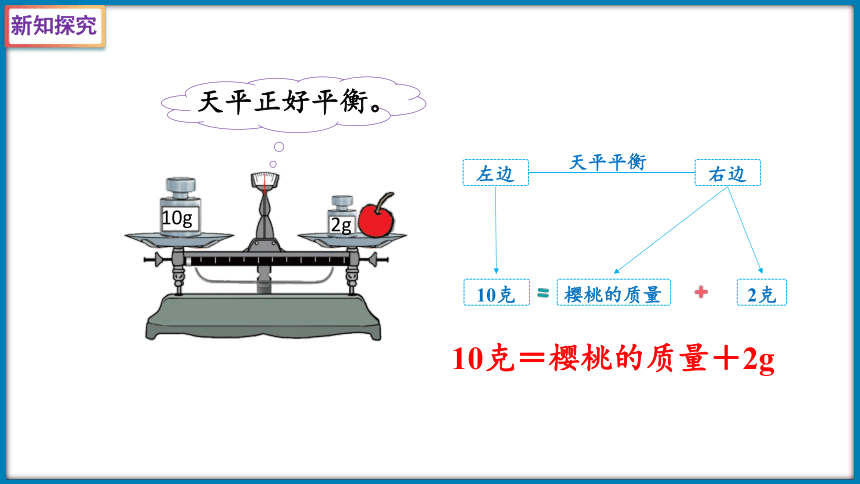
天平正好平衡。
左边
右边
天平平衡
10克
樱桃的质量
2克
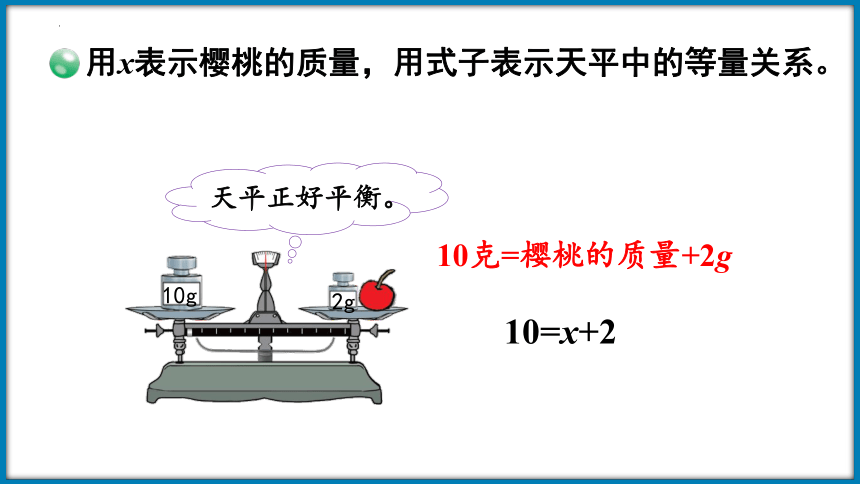
10克=樱桃的质量+2g
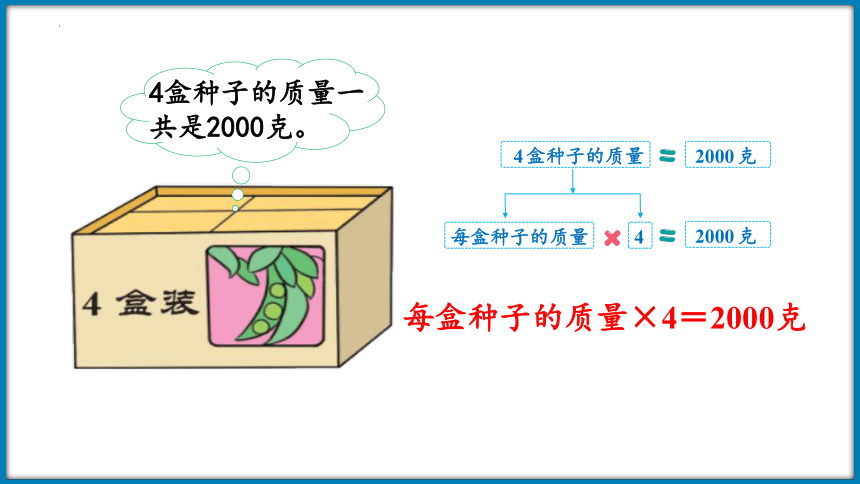
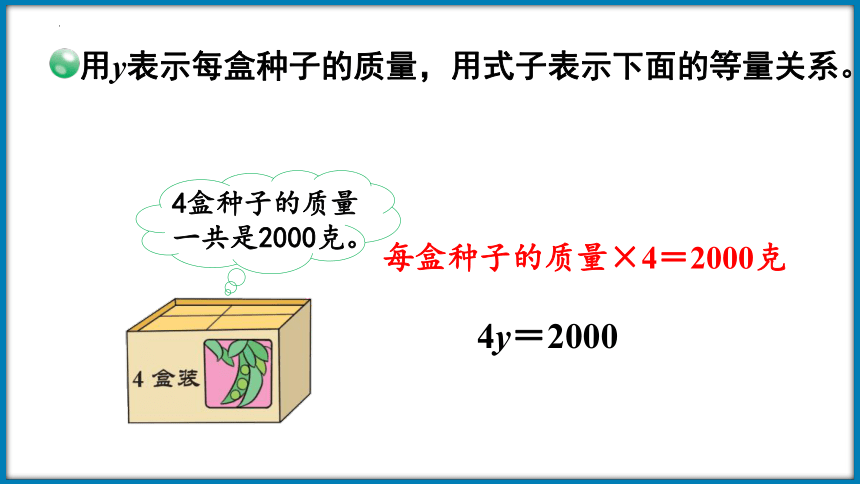
4盒种子的质量一共是2000克。
4盒种子的质量
2000克
每盒种子的质量
4
2000克
每盒种子的质量×4=2000克
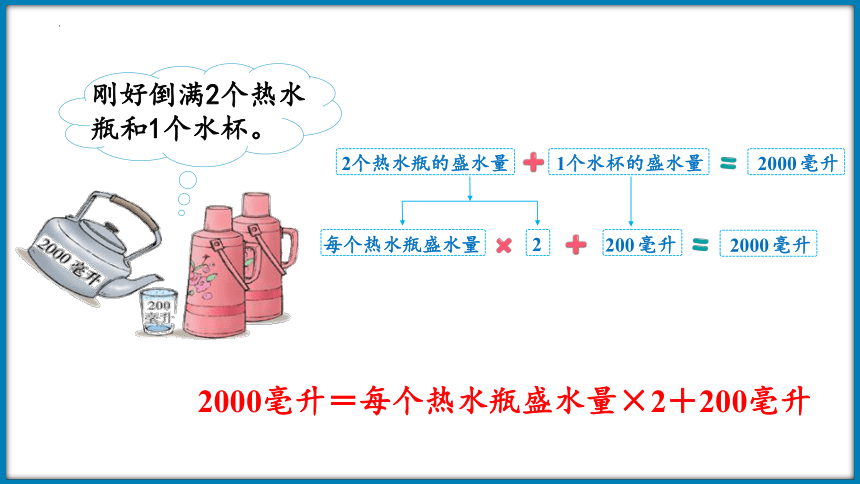
刚好倒满2个热水瓶和1个水杯。
2个热水瓶的盛水量
2000毫升
每个热水瓶盛水量
2
1个水杯的盛水量
200毫升
2000毫升
2000毫升=每个热水瓶盛水量×2+200毫升
10g
2g
10克=樱桃的质量+2g
用x表示樱桃的质量,用式子表示天平中的等量关系。
10=x+2
天平正好平衡。
每盒种子的质量×4=2000克
用y表示每盒种子的质量,用式子表示下面的等量关系。
4y=2000
4盒种子的质量一共是2000克。
2000毫升=每个热水瓶盛水量×2+200毫升
用z表示每个热水瓶的盛水量,用式子表示下面的等量关系。
2000=2z+200
刚好倒满2个热水瓶和1个水杯。
这些等式有什么特点?与同伴进行交流。
2000=2z+200
4y=2000
10=x+2
用等号将相等的量连接起来,表示相等关系的
式子就是等式。
等式
像200+2z=2000,4y=2000 10=x+2 这样,根据等量关系列出的含有未知数的等式就是方程。
等式
未知数
不等式
x+ 20 <100
x + 20 > 50
10 < 100
等式
不含未知数
100+100=200
x + 20 = 70
方程
2 x = 150
3 x + 10 = 100
x + 10 = 15
分类整理
含有未知数
等式不一定是方程。
方程一定是等式。
等式和方程的关系:
等式
方程
以上式子都是方程。
x+5
15+5=20
x ÷5<20
易错提醒
×
未能正确掌握方程的意义。
含有未知数的等式,叫作方程。
正确解答
以上式子都不是方程。第一个不是等式,第二个不含未知数,第三个不是等式。
x+5
15+5=20
x ÷5<20
错因分析
你能自己写出一些方程吗?
x+5=18 x+x+x+x=35 8-x=3
5x=30 x÷4=6 3x+6=12
6(x-2)=24 (x+4)÷2=3 x+y=5
公元250年前后,古希腊数学家丢番图写了一本数学巨著《算术》,引入了未知数的概念,并使用符号表示未知数,这是数学史上的一个重要事件,开启了符号代数的大门。因此,人们常常称丢图番为“代数之父”。
1.选一选。
下列式子中,等式有( C )个,方程有( B )个。
①2x+8 ②a+1.5=7 ③48+16=64
④6x+7=25
C
B
⑤2y-1.8>4.2 ⑥6a2=24
A.2 B.3 C.4
解析:含有等号的式子就是等式,②③④⑥是等式;含有未知数的等式才是方程,②④⑥是方程。
课堂练习
2.下面的式子,是方程的在括号里画“√”,不是的画“ ”。
(1)(9+x)×2 ( )
(2)2-x=0 ( √ )
(3)14÷a=7 ( √ )
(4)7x+3<9 ( )
(5)x=8 ( √ )
(6)16+7=23 ( )
√
√
√
3.看图列方程。
(1)
70+x=100
(2)
3x+100=220
3a+156=208
解析:由图可知,3个a米加上156米等于208米,据此列出方程。
(3)
4.根据描述列方程。
(1)x的1.7倍减去1.5,差是5.3。
1.7x-1.5=5.3
解析:x的1.7倍即1.7x,减去1.5,差是5.3,所以1.7x-1.5=5.3。
(2)x的8倍加上13,和是37。
8x+13=37
解析:x的8倍即8x,加上13,和是37,所以8x+13=37。
5.根据题意先写出等量关系,再列出方程。
(1)商店有15箱鸡蛋,每箱15千克,后来又运来x千克鸡蛋,
现在有480千克鸡蛋,那么
。
方程:15×15+x=480
(2)一套家具有1张桌子和4把椅子,共1200元。桌子的单价
是800元,椅子的单价是x元,那么
。
方程:800+4x=1200
原有鸡蛋的质量+运来鸡蛋的
质量=现有鸡蛋的质量
15×15+x=480
1张桌子的价格+4把
椅子的价格=1200元
800+4x=1200
6. 用方程表示下面的数量关系。
x ÷ 32 = 2
32 – x + 5 = 28
(2)书柜里原有32本故事书,借走x本,今天又新买5本,现在书柜里共有28本。
(1)王老师买了x 个气球,平均分给 32 个学生,每人分得 2个,正好分完。
气球总数
学生人数
每人分得的气球数
÷
=
原有本数
借出本数
现有本数
-
=
新买本数
+
7.根据题意列方程。
四(1) 班有50人,四(2) 班有x人,如果从四(2) 班调3人到四(1) 班,则两个班的人数相等。
x-3=50+3
解析:“从四(2)班调3人到四(1)班”即四(2)班减少3人,四(1)班增加3人,此时两个班的人数相等,所以列出等量关系:四(2)班的人数-3人=四(1)班的人数+3人,据此列出方程。
认真观察下图阴影方框中正中间的数与其他四个数的关系。
⑴中间数是 y,左边的是 ,
右边的数是 ,上面的数是
,下面的数是 。
⑵方框中5个数之和与中间的
数有什么关系?
(3)当5个数的和是115时,中间的数是多少?
5y
23
y-1
y +1
y -7
y +7
1.日历表的规律。
思维拓展
2.如图,大正方形的边长为a,小正方形的边长为b。若拼
成的大长方形的周长为24,列出一个只含有
字母b的关于周长的方程。
11b=24
解析:据图可知,两个大正方形的边长等于三个小正方形的边长,即2a=3b,拼成的大长方形的长是3b,宽是a+b,其周长是(3b+a+b)×2,化简得8b+2a,将2a换成3b,即8b+2a=8b+3b=11b,根据大长方形的周长是24,列出方程:11b=24。
含有未知数的等式,叫作方程。
方程要具备两个条件:
(1)含有未知数,(2)是等式。
方程一定是等式。等式不一定是方程。
这节课你们都学会了哪些知识?
等式
方程
北师版四年级数学下册
认识方程
第3节 方程
汇报人:XXX 时间:XXXXX
1.结合具体情境了解方程的意义,会用方程表示简单情境中的等量关系。
2.经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。
3.在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
4.理解方程的意义,会用方程表示简单情景中的等量关系。
5.找准实际问题中的等量关系。
学习目标
天平
天平是一种衡器,是衡量物体质量的仪器。在杠杆的两端各有一小盘,一端放砝码,另一端放要称的物体,杠杆中央装有指针,两端平衡时,两端的质量(重量)相等。
物体
砝码
课堂导入
观察天平上的指针,发现指针指向正中间,说明天平平衡。
物品
砝码
中央刻度线
天平是怎么用的?
天平平衡,说明左右两边物体的质量相等。
物品
砝码
中央刻度线
左边的物品重
指针左偏
天平是怎么用的?
物品
砝码
左边的物品重
指针左偏
右边的砝码重
指针右偏
中央刻度线
天平是怎么用的?
10g
2g
天平正好平衡。
左边
右边
天平平衡
10克
樱桃的质量
2克
10克=樱桃的质量+2g
4盒种子的质量一共是2000克。
4盒种子的质量
2000克
每盒种子的质量
4
2000克
每盒种子的质量×4=2000克
刚好倒满2个热水瓶和1个水杯。
2个热水瓶的盛水量
2000毫升
每个热水瓶盛水量
2
1个水杯的盛水量
200毫升
2000毫升
2000毫升=每个热水瓶盛水量×2+200毫升
10g
2g
10克=樱桃的质量+2g
用x表示樱桃的质量,用式子表示天平中的等量关系。
10=x+2
天平正好平衡。
每盒种子的质量×4=2000克
用y表示每盒种子的质量,用式子表示下面的等量关系。
4y=2000
4盒种子的质量一共是2000克。
2000毫升=每个热水瓶盛水量×2+200毫升
用z表示每个热水瓶的盛水量,用式子表示下面的等量关系。
2000=2z+200
刚好倒满2个热水瓶和1个水杯。
这些等式有什么特点?与同伴进行交流。
2000=2z+200
4y=2000
10=x+2
用等号将相等的量连接起来,表示相等关系的
式子就是等式。
等式
像200+2z=2000,4y=2000 10=x+2 这样,根据等量关系列出的含有未知数的等式就是方程。
等式
未知数
不等式
x+ 20 <100
x + 20 > 50
10 < 100
等式
不含未知数
100+100=200
x + 20 = 70
方程
2 x = 150
3 x + 10 = 100
x + 10 = 15
分类整理
含有未知数
等式不一定是方程。
方程一定是等式。
等式和方程的关系:
等式
方程
以上式子都是方程。
x+5
15+5=20
x ÷5<20
易错提醒
×
未能正确掌握方程的意义。
含有未知数的等式,叫作方程。
正确解答
以上式子都不是方程。第一个不是等式,第二个不含未知数,第三个不是等式。
x+5
15+5=20
x ÷5<20
错因分析
你能自己写出一些方程吗?
x+5=18 x+x+x+x=35 8-x=3
5x=30 x÷4=6 3x+6=12
6(x-2)=24 (x+4)÷2=3 x+y=5
公元250年前后,古希腊数学家丢番图写了一本数学巨著《算术》,引入了未知数的概念,并使用符号表示未知数,这是数学史上的一个重要事件,开启了符号代数的大门。因此,人们常常称丢图番为“代数之父”。
1.选一选。
下列式子中,等式有( C )个,方程有( B )个。
①2x+8 ②a+1.5=7 ③48+16=64
④6x+7=25
C
B
⑤2y-1.8>4.2 ⑥6a2=24
A.2 B.3 C.4
解析:含有等号的式子就是等式,②③④⑥是等式;含有未知数的等式才是方程,②④⑥是方程。
课堂练习
2.下面的式子,是方程的在括号里画“√”,不是的画“ ”。
(1)(9+x)×2 ( )
(2)2-x=0 ( √ )
(3)14÷a=7 ( √ )
(4)7x+3<9 ( )
(5)x=8 ( √ )
(6)16+7=23 ( )
√
√
√
3.看图列方程。
(1)
70+x=100
(2)
3x+100=220
3a+156=208
解析:由图可知,3个a米加上156米等于208米,据此列出方程。
(3)
4.根据描述列方程。
(1)x的1.7倍减去1.5,差是5.3。
1.7x-1.5=5.3
解析:x的1.7倍即1.7x,减去1.5,差是5.3,所以1.7x-1.5=5.3。
(2)x的8倍加上13,和是37。
8x+13=37
解析:x的8倍即8x,加上13,和是37,所以8x+13=37。
5.根据题意先写出等量关系,再列出方程。
(1)商店有15箱鸡蛋,每箱15千克,后来又运来x千克鸡蛋,
现在有480千克鸡蛋,那么
。
方程:15×15+x=480
(2)一套家具有1张桌子和4把椅子,共1200元。桌子的单价
是800元,椅子的单价是x元,那么
。
方程:800+4x=1200
原有鸡蛋的质量+运来鸡蛋的
质量=现有鸡蛋的质量
15×15+x=480
1张桌子的价格+4把
椅子的价格=1200元
800+4x=1200
6. 用方程表示下面的数量关系。
x ÷ 32 = 2
32 – x + 5 = 28
(2)书柜里原有32本故事书,借走x本,今天又新买5本,现在书柜里共有28本。
(1)王老师买了x 个气球,平均分给 32 个学生,每人分得 2个,正好分完。
气球总数
学生人数
每人分得的气球数
÷
=
原有本数
借出本数
现有本数
-
=
新买本数
+
7.根据题意列方程。
四(1) 班有50人,四(2) 班有x人,如果从四(2) 班调3人到四(1) 班,则两个班的人数相等。
x-3=50+3
解析:“从四(2)班调3人到四(1)班”即四(2)班减少3人,四(1)班增加3人,此时两个班的人数相等,所以列出等量关系:四(2)班的人数-3人=四(1)班的人数+3人,据此列出方程。
认真观察下图阴影方框中正中间的数与其他四个数的关系。
⑴中间数是 y,左边的是 ,
右边的数是 ,上面的数是
,下面的数是 。
⑵方框中5个数之和与中间的
数有什么关系?
(3)当5个数的和是115时,中间的数是多少?
5y
23
y-1
y +1
y -7
y +7
1.日历表的规律。
思维拓展
2.如图,大正方形的边长为a,小正方形的边长为b。若拼
成的大长方形的周长为24,列出一个只含有
字母b的关于周长的方程。
11b=24
解析:据图可知,两个大正方形的边长等于三个小正方形的边长,即2a=3b,拼成的大长方形的长是3b,宽是a+b,其周长是(3b+a+b)×2,化简得8b+2a,将2a换成3b,即8b+2a=8b+3b=11b,根据大长方形的周长是24,列出方程:11b=24。
含有未知数的等式,叫作方程。
方程要具备两个条件:
(1)含有未知数,(2)是等式。
方程一定是等式。等式不一定是方程。
这节课你们都学会了哪些知识?
等式
方程
