四年级下册数学北师大版第五单元5.2 字母表示数(用字母表示公式和运算律)课件(共26张PPT)
文档属性
| 名称 | 四年级下册数学北师大版第五单元5.2 字母表示数(用字母表示公式和运算律)课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 19:04:06 | ||
图片预览



文档简介
(共26张PPT)
北师版四年级数学下册
认识方程
第1节 字母表示数 第2课时
汇报人:XXX 时间:XXXXX
1.结合具体情境,会用字母表示数和数量关系,能用字母表示运算律和有关图形的计算公式。
2.经历探索用字母表示数的过程,体会用字母表示数的必要性,发展抽象概括能力,渗透函数思想。
3.能用字母表述数、数量关系、运算律和有关图形的计算公式。
4.理解用字母表示数的意义。
学习目标
25+36=36+( )
13×(8+9)=13×( )+13×( )
25
知识回顾
加法交换律
(28+37)+22=37+( )
28+22
加法结合律
23×42=42×( )
23
乘法交换律
(25×13)×40=13×( )
25×40
乘法结合律
8
9
乘法分配律
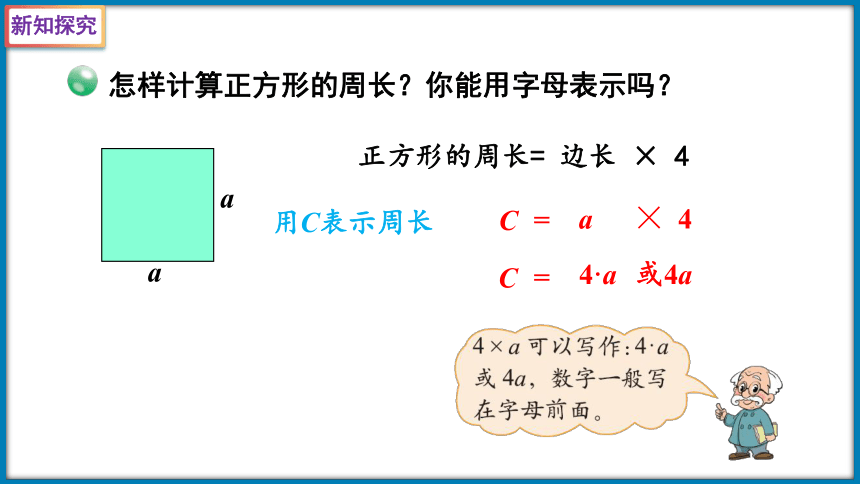
怎样计算正方形的周长?你能用字母表示吗?
正方形的周长= 边长 × 4
a
a
用C表示周长
C
=
a
×
4
C
=
4·a
或4a
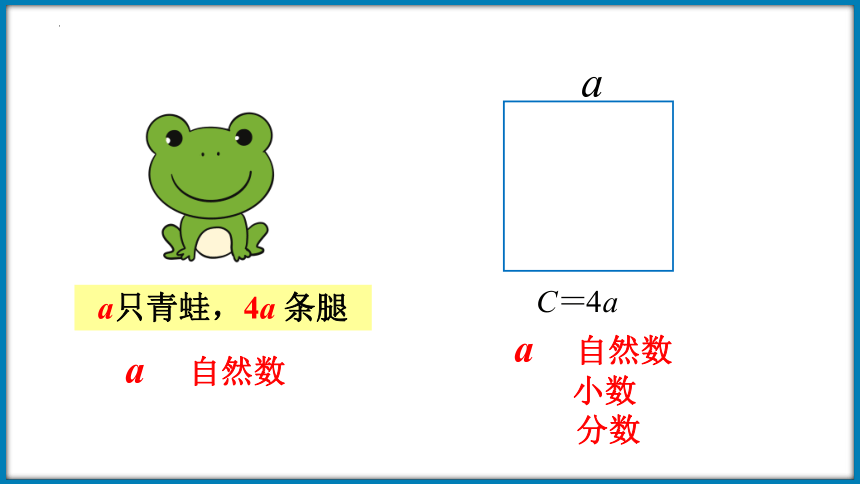
a只青蛙,4a 条腿
a 自然数
a 自然数
小数
分数
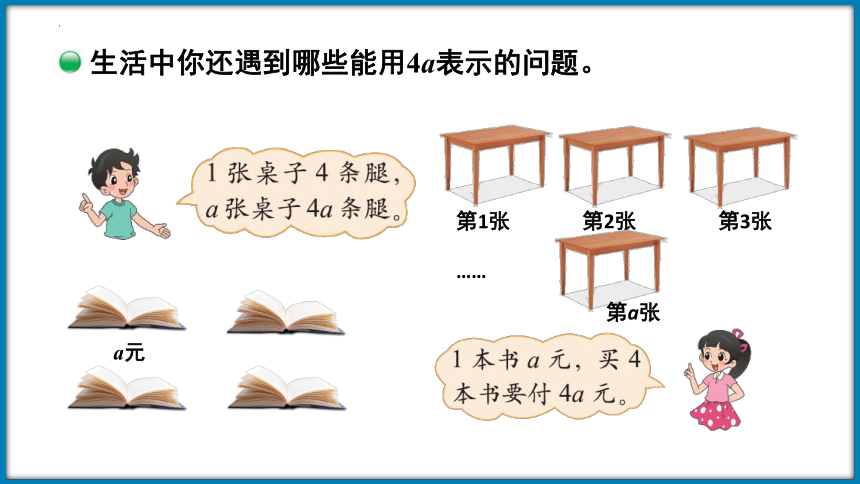
生活中你还遇到哪些能用4a表示的问题。
第1张
第2张
第3张
第a张
……
a元
a
a
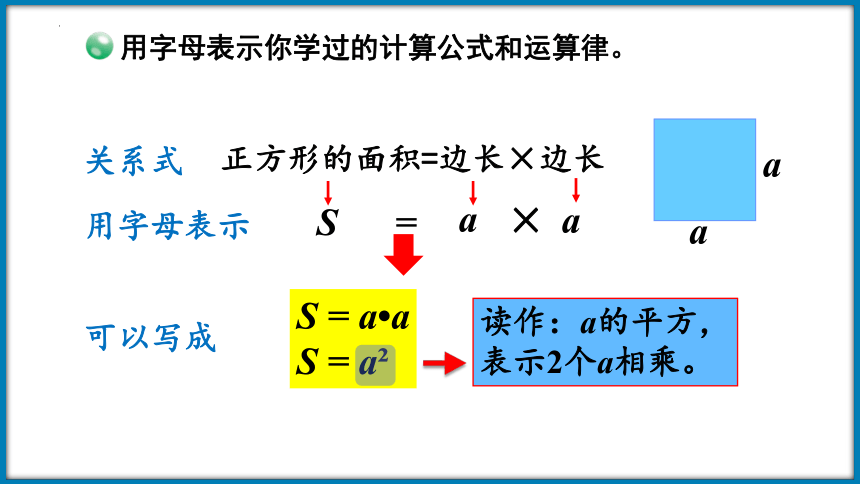
关系式
正方形的面积=边长×边长
用字母表示
a
a
S
=
×
可以写成
S = a a
S = a
读作:a的平方,
表示2个a相乘。
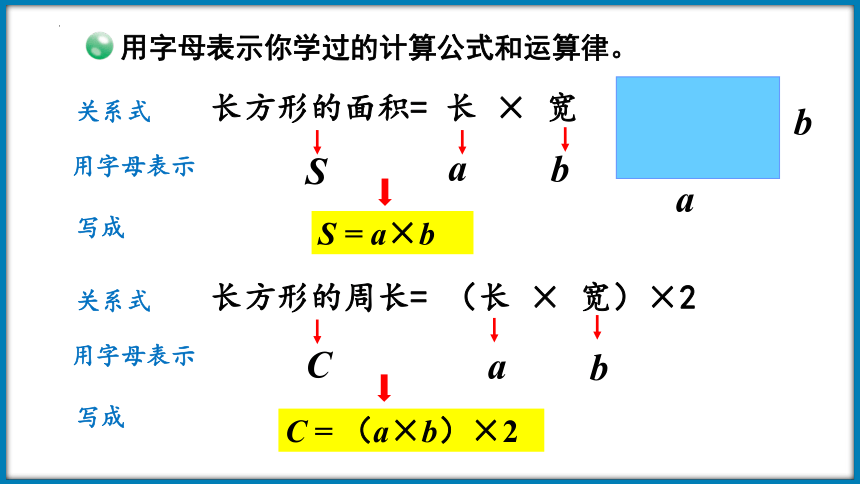
用字母表示你学过的计算公式和运算律。
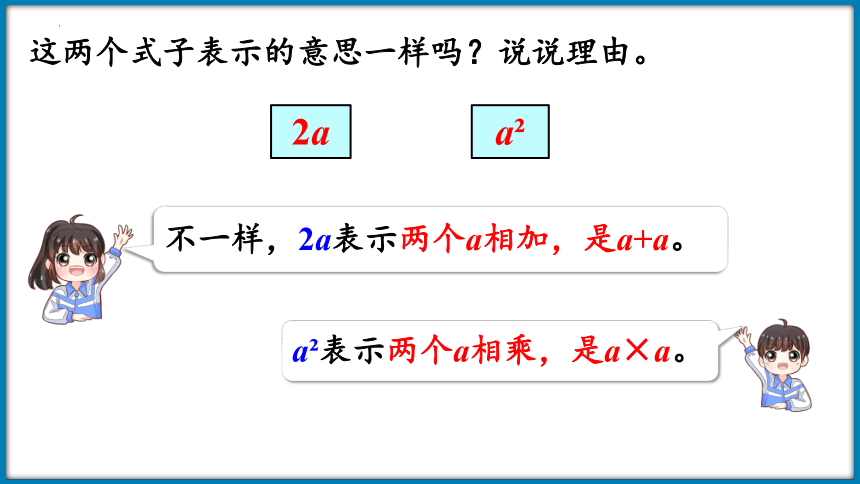
2a
这两个式子表示的意思一样吗?说说理由。
a
不一样,2a表示两个a相加,是a+a。
a 表示两个a相乘,是a×a。
b
a
关系式
长方形的面积= 长 × 宽
用字母表示
a
b
S
写成
用字母表示你学过的计算公式和运算律。
S = a×b
关系式
长方形的周长= (长 × 宽)×2
用字母表示
a
b
C
写成
C = (a×b)×2
我们已经学过一些运算律,你会用字母表示吗?
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α×b=b×α
(α×b)×c=α×(b×c)
(α+b)×c=α×c+b×c
α+b=b+α
我们学过的运算律有哪些呢?
在含有字母的式子里,字母中间的乘号可以记作“ · ”,也可以省略不写。
注意:这种省略仅限于乘号,加、减、除号不能省略。
a×b=b×a
可以写成 a b=b a
×
×
或 ab=ba
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α×b=b×α
(α×b)×c=α×(b×c)
(α+b)×c=α×c+b×c
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
用字母表示运算定律,简明易记、便于应用。
运算律 用语言描述
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
两个数相加,交换加数的位置,和不变。
三个数相加,先把前两个数相加,或者先
把后两个数相加,结果不变。
两个数相乘,交换因数的位置,积不变。
三个数相乘,先把前两个数相乘,或者先
把后两个数相乘,结果不变。
两个数的和同一个数相乘,可以先把这两个加数
分别同这个数相乘,再把两个积相加,结果不变。
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
02
03
用字母表示计算公式和运算定律比文字叙述更简明易记、便于应用。
01
在含有字母的式子里,数字和字母中间的乘号可以记作“·” ,也可以省略不写,但数字必须写在字母的前边。
a 读作a的平方,表示两个a 相乘,2a表示两个a相加。
课堂小结
同学们,这节课你们学会了哪些知识?
1.省略乘号,写出下面的式子。
3×b=3b x×6=6x x×2y=2xy
c×a=ca x×y=xy 5.6×b=5.6b
1×x=x m×n=mn x×b×h=xbh
解析:数字与字母相乘时,乘号可以省略,数字一般写在字母的前面。
3b
6x
2xy
ca
xy
5.6b
x
mn
xbh
课堂练习
2.想一想,填一填。
(1)粮食仓储区的周长是( 2(a+b)或2a+2b ),面
积是( ab )。调料品仓储区的周长是( 4a ),面积是
( a2 )。这个图形的总面积是( ab+ac或a(b+c) )。
2(a+b)或2a+2b
ab
4a
a2
解析:分清每个长方形的长和宽,再根据“长方形的面积=长×宽”填写。
ab+a2或a(b+a)
(2)每本练习本x元,买了6本,付了10元,应找回( 10- )元。
(3)货车每时行n千米,客车每时行m千米,客车行了3时,货
车行了5时,一共行了( 3m+5n )千米。
10-6x
3m+5n
(4)如图(单位:厘米),阴影部分的面积是( a2-b2 )平方厘米。
解析:正方形的面积=边长×边长,分别求出大正方形和小正方形的面积,则阴影部分的面积等于大正方形的面积减去小正方形的面积。
a2-b2
(5) 当a=0.2时,2a=( 0.4 ),a2=( 0.04 )。
解析:当a=0.2时,2a=2×0.2=0.4,a2=0.2×0.2=0.04。
(6)一个等腰三角形的顶角是n°,则它的底角是
( (180°-n°)÷2 )。
解析:三角形的内角和是180°,等腰三角形的底角相等,所以一个底角的度数等于(180°-顶角的度数)÷2。
0.4
0.04
(180°-n°)÷2
3.根据运算律填空。
(1)m×2.5×0.4= m ×( 2.5 × 0.4 )
解析:依据乘法结合律;
(2)(a-b)×c= a × c - b × c
解析:依据乘法分配律;
(3)7.2x+2.8x=( 7.2 + 2.8 )× x
解析:依据乘法分配律;
(4)a÷ b ÷ 5 =a÷(b×5)
解析:依据除法的性质。
m
2.5
0.4
a
c
b
c
7.2
2.8
x
b
5
4.填表。
时间(时) 速度(千米/时) 路程(千米)
自行车 3 s÷3 s
小汽车 t 60 60t
火车 880÷v v 880
s÷3
60t
880÷v
5、将长方形的四个角分别剪去一个边长为m的小正方形。求剩余图形的周长和面积。
周长:2a+2b
面积:ab-4m
6.如图中,空白部分是一个正方形。用含有字母的式子表
示空白部分和阴影部分的面积。当a=8 cm,b=12 cm
时,求空白部分和阴影部分的面积。
阴影部分面积:ab-a2
当a=8 cm时,a2=8×8=64(cm2),即空白部分的面积是64 cm2。当a=8 cm,b=12 cm时,
ab-a2=8×12-8×8=32(cm2),即阴影部分的面积是32 cm2。
空白部分面积:a2
解析:根据题意可知,空白部分是一个正方形,且边长是a,所以大长方形的宽是a,则空白部分的面积是a2,大长方形的面积是ab,阴影部分的面积等于大长方形的面积减去正方形的面积。最后把数值代入式子进行计算。
1.乐乐用圆和正方形摆图形。
序号 第1个 第2个 第3个 … 第n个
所需正方 形个数 1 2 3 … n
所需圆 个数 4 8 12 … 4n
1
2
3
n
4
8
12
4n
思维拓展
2.用小棒按照如下方式摆图形。
摆1个八边形需要8根小棒,摆2个八边形需要( 15 )根
小棒,摆3个八边形需要( 22 )根小棒,摆n个八边形
需要( 7n+1 )根小棒。
15
22
7n+1
解析:观察发现,每多摆1个八边形需增加7根小棒,则摆2个八边形需要8+7=15(根)小棒,摆3个八边形需要8+7×2=22(根)小棒,摆n个八边形需要8+7×(n-1)=(7n+1)(根)小棒。
A=X+Y+Z
A表成功,
X代表艰苦的劳动,
Y代表正确的方法,
Z代表少说空话。
成功的公式
课堂小结
北师版四年级数学下册
认识方程
第1节 字母表示数 第2课时
汇报人:XXX 时间:XXXXX
1.结合具体情境,会用字母表示数和数量关系,能用字母表示运算律和有关图形的计算公式。
2.经历探索用字母表示数的过程,体会用字母表示数的必要性,发展抽象概括能力,渗透函数思想。
3.能用字母表述数、数量关系、运算律和有关图形的计算公式。
4.理解用字母表示数的意义。
学习目标
25+36=36+( )
13×(8+9)=13×( )+13×( )
25
知识回顾
加法交换律
(28+37)+22=37+( )
28+22
加法结合律
23×42=42×( )
23
乘法交换律
(25×13)×40=13×( )
25×40
乘法结合律
8
9
乘法分配律
怎样计算正方形的周长?你能用字母表示吗?
正方形的周长= 边长 × 4
a
a
用C表示周长
C
=
a
×
4
C
=
4·a
或4a
a只青蛙,4a 条腿
a 自然数
a 自然数
小数
分数
生活中你还遇到哪些能用4a表示的问题。
第1张
第2张
第3张
第a张
……
a元
a
a
关系式
正方形的面积=边长×边长
用字母表示
a
a
S
=
×
可以写成
S = a a
S = a
读作:a的平方,
表示2个a相乘。
用字母表示你学过的计算公式和运算律。
2a
这两个式子表示的意思一样吗?说说理由。
a
不一样,2a表示两个a相加,是a+a。
a 表示两个a相乘,是a×a。
b
a
关系式
长方形的面积= 长 × 宽
用字母表示
a
b
S
写成
用字母表示你学过的计算公式和运算律。
S = a×b
关系式
长方形的周长= (长 × 宽)×2
用字母表示
a
b
C
写成
C = (a×b)×2
我们已经学过一些运算律,你会用字母表示吗?
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α×b=b×α
(α×b)×c=α×(b×c)
(α+b)×c=α×c+b×c
α+b=b+α
我们学过的运算律有哪些呢?
在含有字母的式子里,字母中间的乘号可以记作“ · ”,也可以省略不写。
注意:这种省略仅限于乘号,加、减、除号不能省略。
a×b=b×a
可以写成 a b=b a
×
×
或 ab=ba
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α×b=b×α
(α×b)×c=α×(b×c)
(α+b)×c=α×c+b×c
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
用字母表示运算定律,简明易记、便于应用。
运算律 用语言描述
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
两个数相加,交换加数的位置,和不变。
三个数相加,先把前两个数相加,或者先
把后两个数相加,结果不变。
两个数相乘,交换因数的位置,积不变。
三个数相乘,先把前两个数相乘,或者先
把后两个数相乘,结果不变。
两个数的和同一个数相乘,可以先把这两个加数
分别同这个数相乘,再把两个积相加,结果不变。
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
02
03
用字母表示计算公式和运算定律比文字叙述更简明易记、便于应用。
01
在含有字母的式子里,数字和字母中间的乘号可以记作“·” ,也可以省略不写,但数字必须写在字母的前边。
a 读作a的平方,表示两个a 相乘,2a表示两个a相加。
课堂小结
同学们,这节课你们学会了哪些知识?
1.省略乘号,写出下面的式子。
3×b=3b x×6=6x x×2y=2xy
c×a=ca x×y=xy 5.6×b=5.6b
1×x=x m×n=mn x×b×h=xbh
解析:数字与字母相乘时,乘号可以省略,数字一般写在字母的前面。
3b
6x
2xy
ca
xy
5.6b
x
mn
xbh
课堂练习
2.想一想,填一填。
(1)粮食仓储区的周长是( 2(a+b)或2a+2b ),面
积是( ab )。调料品仓储区的周长是( 4a ),面积是
( a2 )。这个图形的总面积是( ab+ac或a(b+c) )。
2(a+b)或2a+2b
ab
4a
a2
解析:分清每个长方形的长和宽,再根据“长方形的面积=长×宽”填写。
ab+a2或a(b+a)
(2)每本练习本x元,买了6本,付了10元,应找回( 10- )元。
(3)货车每时行n千米,客车每时行m千米,客车行了3时,货
车行了5时,一共行了( 3m+5n )千米。
10-6x
3m+5n
(4)如图(单位:厘米),阴影部分的面积是( a2-b2 )平方厘米。
解析:正方形的面积=边长×边长,分别求出大正方形和小正方形的面积,则阴影部分的面积等于大正方形的面积减去小正方形的面积。
a2-b2
(5) 当a=0.2时,2a=( 0.4 ),a2=( 0.04 )。
解析:当a=0.2时,2a=2×0.2=0.4,a2=0.2×0.2=0.04。
(6)一个等腰三角形的顶角是n°,则它的底角是
( (180°-n°)÷2 )。
解析:三角形的内角和是180°,等腰三角形的底角相等,所以一个底角的度数等于(180°-顶角的度数)÷2。
0.4
0.04
(180°-n°)÷2
3.根据运算律填空。
(1)m×2.5×0.4= m ×( 2.5 × 0.4 )
解析:依据乘法结合律;
(2)(a-b)×c= a × c - b × c
解析:依据乘法分配律;
(3)7.2x+2.8x=( 7.2 + 2.8 )× x
解析:依据乘法分配律;
(4)a÷ b ÷ 5 =a÷(b×5)
解析:依据除法的性质。
m
2.5
0.4
a
c
b
c
7.2
2.8
x
b
5
4.填表。
时间(时) 速度(千米/时) 路程(千米)
自行车 3 s÷3 s
小汽车 t 60 60t
火车 880÷v v 880
s÷3
60t
880÷v
5、将长方形的四个角分别剪去一个边长为m的小正方形。求剩余图形的周长和面积。
周长:2a+2b
面积:ab-4m
6.如图中,空白部分是一个正方形。用含有字母的式子表
示空白部分和阴影部分的面积。当a=8 cm,b=12 cm
时,求空白部分和阴影部分的面积。
阴影部分面积:ab-a2
当a=8 cm时,a2=8×8=64(cm2),即空白部分的面积是64 cm2。当a=8 cm,b=12 cm时,
ab-a2=8×12-8×8=32(cm2),即阴影部分的面积是32 cm2。
空白部分面积:a2
解析:根据题意可知,空白部分是一个正方形,且边长是a,所以大长方形的宽是a,则空白部分的面积是a2,大长方形的面积是ab,阴影部分的面积等于大长方形的面积减去正方形的面积。最后把数值代入式子进行计算。
1.乐乐用圆和正方形摆图形。
序号 第1个 第2个 第3个 … 第n个
所需正方 形个数 1 2 3 … n
所需圆 个数 4 8 12 … 4n
1
2
3
n
4
8
12
4n
思维拓展
2.用小棒按照如下方式摆图形。
摆1个八边形需要8根小棒,摆2个八边形需要( 15 )根
小棒,摆3个八边形需要( 22 )根小棒,摆n个八边形
需要( 7n+1 )根小棒。
15
22
7n+1
解析:观察发现,每多摆1个八边形需增加7根小棒,则摆2个八边形需要8+7=15(根)小棒,摆3个八边形需要8+7×2=22(根)小棒,摆n个八边形需要8+7×(n-1)=(7n+1)(根)小棒。
A=X+Y+Z
A表成功,
X代表艰苦的劳动,
Y代表正确的方法,
Z代表少说空话。
成功的公式
课堂小结
