第九章 统计 章末复习课 学案(含答案)
文档属性
| 名称 | 第九章 统计 章末复习课 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 296.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 17:54:46 | ||
图片预览


文档简介
第九章 统计 章末复习课
一、抽样方法的选取及应用
1.三种抽样方法的适用范围:当总体容量较小,样本容量也较小时,可采用抽签法;当总体容量较大,样本容量较小时,可采用随机数法;当总体中个体差异较显著时,可采用分层随机抽样,但是要明确是否按比例分配.
2.掌握不同抽样方法,提升数据分析素养.
例1 某学校在校学生有3 000人,为了增强学生的体质,学校举行了跑步和登山比赛,每人都参加且只参加其中一项比赛,高一、高二、高三年级参加跑步的人数分别为a,b,c,且a∶b∶c=2∶3∶4,全校参加登山的人数占总人数的.为了了解学生对本次比赛的满意程度,按比例分配的分层随机抽样的方法从中抽取一个容量为300的样本进行调查,则应从高二年级参加跑步的学生中抽取( )
A.15人 B.30人 C.45人 D.60人
反思感悟 分层随机抽样仅分层抽取,但如何抽取,情况不确定,如果强调了按比例分配,即按“=”进行抽样.
跟踪训练1 (1)以下抽样方法是简单随机抽样的是( )
A.在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2 709的是三等奖
B.某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽一包产品,称其重量是否合格
C.某学校分别从行政人员、教师、后勤人员中抽取2人、14人、4人了解对学校机构改革的意见
D.用抽签法从10件产品中选取3件进行质量检验
(2)某校为了营造浓厚的校园体育氛围,采用按比例分配的分层随机抽样的方法从高一1 200人、高二1 450人、高三n人中,抽取80人观看排球决赛,已知高一被抽取的人数为24,那么高三年级人数n为( )
A.1 250 B.1 300 C.1 350 D.1 400
二、用样本的取值规律估计总体的取值规律
1.根据样本容量的大小,我们可以选择利用样本的频率分布表、频率分布直方图对总体情况作出估计.
2.掌握频率分布直方图的绘制及应用,提升数据分析和数学运算素养.
例2 为了解高一年级学生的智力水平,某校按1∶10的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如表1、表2.
表1:男生“智力评分”频数分布表
智力评分(分) [160,165) [165,170) [170,175)
频数 2 5 14
智力评分(分) [175,180) [180,185) [185,190]
频数 13 4 2
表2:女生“智力评分”频数分布表
智力评分(分) [150,155) [155,160) [160,165)
频数 1 7 12
智力评分(分) [165,170) [170,175) [175,180]
频数 6 3 1
(1)求高一年级的男生人数,并完成下面男生“智力评分”的频率分布直方图;
(2)估计该校高一年级学生“智力评分”在[165,175)内的人数.
反思感悟 (1)绘制频率分布直方图时需注意的两点
①制作好频率分布表后,可以利用各组的频率之和是否为1来检验该表是否正确;
②频率分布直方图的纵坐标是,而不是频率.
(2)与频率分布直方图计算有关的两个关系式
①×组距=频率;
②=频率,此关系式的变形为=样本容量,样本容量×频率=频数.
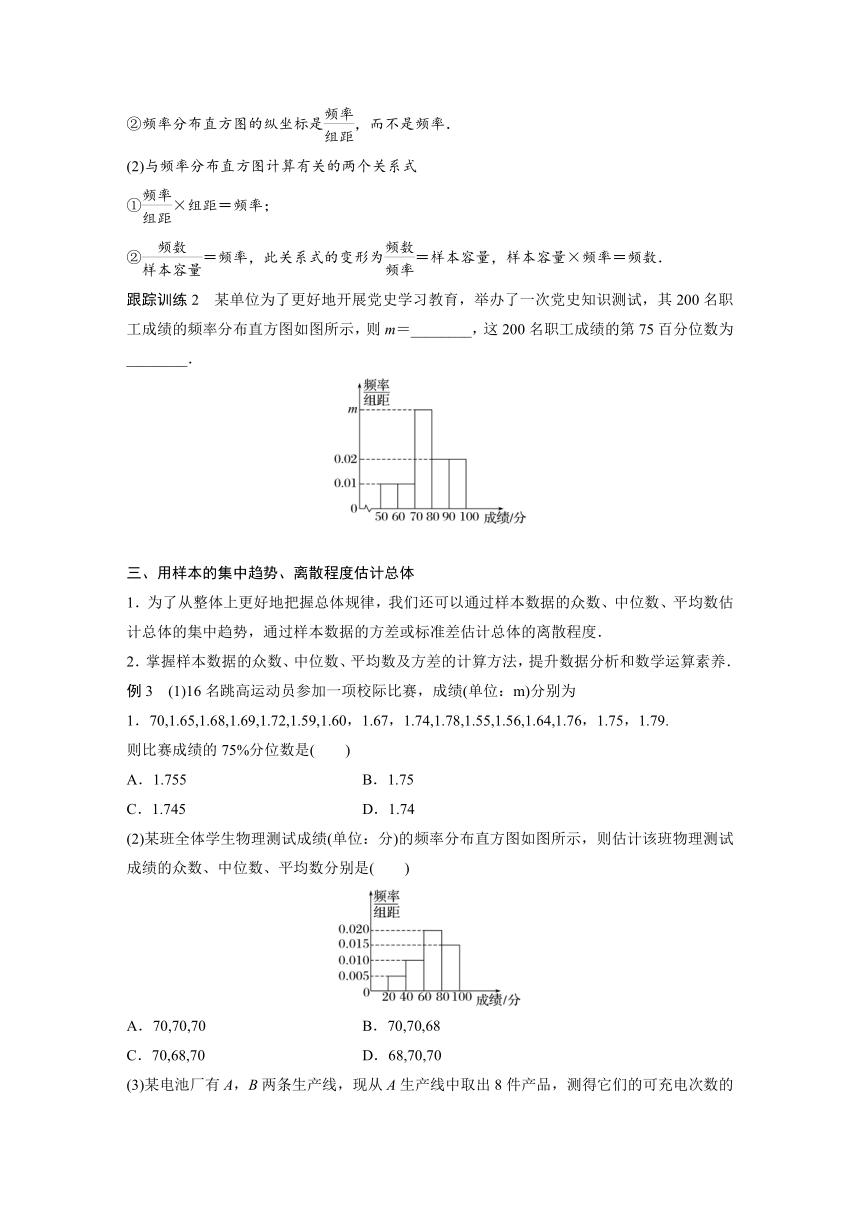
跟踪训练2 某单位为了更好地开展党史学习教育,举办了一次党史知识测试,其200名职工成绩的频率分布直方图如图所示,则m=________,这200名职工成绩的第75百分位数为________.
三、用样本的集中趋势、离散程度估计总体
1.为了从整体上更好地把握总体规律,我们还可以通过样本数据的众数、中位数、平均数估计总体的集中趋势,通过样本数据的方差或标准差估计总体的离散程度.
2.掌握样本数据的众数、中位数、平均数及方差的计算方法,提升数据分析和数学运算素养.
例3 (1)16名跳高运动员参加一项校际比赛,成绩(单位:m)分别为
1.70,1.65,1.68,1.69,1.72,1.59,1.60,1.67,1.74,1.78,1.55,1.56,1.64,1.76,1.75,1.79.
则比赛成绩的75%分位数是( )
A.1.755 B.1.75
C.1.745 D.1.74
(2)某班全体学生物理测试成绩(单位:分)的频率分布直方图如图所示,则估计该班物理测试成绩的众数、中位数、平均数分别是( )
A.70,70,70 B.70,70,68
C.70,68,70 D.68,70,70
(3)某电池厂有A,B两条生产线,现从A生产线中取出8件产品,测得它们的可充电次数的平均数为210,方差为4;从B生产线中取出12件产品,测得它们的可充电次数的平均数为200,方差为4.则这20件产品组成的总样本的方差为________.
反思感悟 通常我们用样本的平均数和方差(标准差)来近似代替总体的平均数和方差(标准差),呈现样本数据的集中趋势及波动大小,从而实现对总体的估计.
(1)一般情况下,需要将平均数和标准差结合,得到更多样本数据的信息,从而对总体作出较好的估计.因为平均数容易掩盖一些极端情况,使我们对总体作出片面的判断,而标准差较好地避免了极端情况.
(2)若两组数据的平均数差别很大,也可以只比较平均数,估计总体的平均水平,从而作出判断.
跟踪训练3 (1)(多选)某班级体温检测员对一周内甲、乙两名同学的体温进行了统计,其结果如图所示,则( )
A.甲同学体温的极差为0.4 ℃
B.乙同学体温的众数为36.4 ℃,中位数与平均数相等
C.乙同学的体温比甲同学的体温稳定
D.甲同学体温的第60百分位数为36.4 ℃
(2)某汽车租赁公司为了调查A型汽车与B型汽车的出租情况,现随机抽取这两种车各50辆,分别统计每辆车在某个星期内的出租天数,统计数据如下表:
A型汽车
出租天数 3 4 5 6 7
车辆数 3 30 5 7 5
B型汽车
出租天数 3 4 5 6 7
车辆数 10 10 15 10 5
①试根据上面的统计数据,判断这两种车在某个星期内的出租天数的方差的大小关系(只需写出结果);
②如果A型汽车与B型汽车每辆车每天出租获得的利润相同,该公司需要购买一辆汽车,请你根据所学的统计知识,给出建议应该购买哪一种车,并说明你的理由.
章末复习课
例1 D 跟踪训练1 (1)D (2)C
例2 解 (1)样本中男生人数是40,由抽样比例是1∶10可得高一年级男生人数是400,
男生“智力评分”的频率分布直方图如图所示.
(2)样本中“智力评分”在[165,175)内的频数为28,所以估计该校高一年级学生“智力评分”在[165,175)内的学生人数为28×10=280.
跟踪训练2 0.04 87.5
例3 (1)C
(2)B [由题意知众数为
=70;
因为(0.005+0.010)×20
=0.3<0.5,
(0.005+0.010+0.020)×20
=0.7>0.5,
所以中位数位于[60,80)中,
设中位数为x,则(0.005+0.010)×20+(x-60)×0.020=0.5,
解得x=70;
平均数为30×0.1+50×0.2+70×0.4+90×0.3=68.]
(3)28
解析 方法一 总样本的平均数
=×210+×200=204,
方差s2=[4+(210-204)2]+[4+(200-204)2]=28.
跟踪训练3 (1)ABC [对于A,甲同学体温的极差为
36.6-36.2=0.4(℃),故A正确;
对于B,乙同学体温为
36.4,36.3,36.5,36.4,36.4,36.3,36.5,其众数为36.4 ℃,中位数、平均数均为36.4 ℃,故B正确;
对于C,根据图中数据,甲同学体温的平均数为36.4 ℃,与乙同学体温的平均数相同,但甲同学的体温极差为0.4 ℃,大于乙同学的体温极差0.2 ℃,而且从图中容易看出乙同学的数据更集中,故乙同学的体温比甲同学的体温稳定,故C正确;
对于D,甲同学的体温从小到大排序为36.2,36.2,36.4,36.4,36.5,36.5,36.6,7×60%=4.2,故甲同学体温的第60百分位数为36.5 ℃,故D错误.]
(2)解 ①由数据的离散程度,可以看出B型汽车在某个星期内出租天数的方差较大.
②50辆A型汽车出租天数的平均数为A=
=4.62,
50辆B型汽车出租天数的平均数为
B=
=4.8,
方案一:A型汽车在某个星期内出租天数的平均数为4.62,B型汽车在某个星期内出租天数的平均数为4.8,选择B型汽车的出租车的利润较大,应该购买B型汽车.
方案二:A型汽车在某个星期内出租天数的平均数为4.62,B型汽车在某个星期内出租天数的平均数为4.8,而B型汽车出租天数的方差较大,所以应该购买A型汽车.
一、抽样方法的选取及应用
1.三种抽样方法的适用范围:当总体容量较小,样本容量也较小时,可采用抽签法;当总体容量较大,样本容量较小时,可采用随机数法;当总体中个体差异较显著时,可采用分层随机抽样,但是要明确是否按比例分配.
2.掌握不同抽样方法,提升数据分析素养.
例1 某学校在校学生有3 000人,为了增强学生的体质,学校举行了跑步和登山比赛,每人都参加且只参加其中一项比赛,高一、高二、高三年级参加跑步的人数分别为a,b,c,且a∶b∶c=2∶3∶4,全校参加登山的人数占总人数的.为了了解学生对本次比赛的满意程度,按比例分配的分层随机抽样的方法从中抽取一个容量为300的样本进行调查,则应从高二年级参加跑步的学生中抽取( )
A.15人 B.30人 C.45人 D.60人
反思感悟 分层随机抽样仅分层抽取,但如何抽取,情况不确定,如果强调了按比例分配,即按“=”进行抽样.
跟踪训练1 (1)以下抽样方法是简单随机抽样的是( )
A.在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2 709的是三等奖
B.某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽一包产品,称其重量是否合格
C.某学校分别从行政人员、教师、后勤人员中抽取2人、14人、4人了解对学校机构改革的意见
D.用抽签法从10件产品中选取3件进行质量检验
(2)某校为了营造浓厚的校园体育氛围,采用按比例分配的分层随机抽样的方法从高一1 200人、高二1 450人、高三n人中,抽取80人观看排球决赛,已知高一被抽取的人数为24,那么高三年级人数n为( )
A.1 250 B.1 300 C.1 350 D.1 400
二、用样本的取值规律估计总体的取值规律
1.根据样本容量的大小,我们可以选择利用样本的频率分布表、频率分布直方图对总体情况作出估计.
2.掌握频率分布直方图的绘制及应用,提升数据分析和数学运算素养.
例2 为了解高一年级学生的智力水平,某校按1∶10的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如表1、表2.
表1:男生“智力评分”频数分布表
智力评分(分) [160,165) [165,170) [170,175)
频数 2 5 14
智力评分(分) [175,180) [180,185) [185,190]
频数 13 4 2
表2:女生“智力评分”频数分布表
智力评分(分) [150,155) [155,160) [160,165)
频数 1 7 12
智力评分(分) [165,170) [170,175) [175,180]
频数 6 3 1
(1)求高一年级的男生人数,并完成下面男生“智力评分”的频率分布直方图;
(2)估计该校高一年级学生“智力评分”在[165,175)内的人数.
反思感悟 (1)绘制频率分布直方图时需注意的两点
①制作好频率分布表后,可以利用各组的频率之和是否为1来检验该表是否正确;
②频率分布直方图的纵坐标是,而不是频率.
(2)与频率分布直方图计算有关的两个关系式
①×组距=频率;
②=频率,此关系式的变形为=样本容量,样本容量×频率=频数.
跟踪训练2 某单位为了更好地开展党史学习教育,举办了一次党史知识测试,其200名职工成绩的频率分布直方图如图所示,则m=________,这200名职工成绩的第75百分位数为________.
三、用样本的集中趋势、离散程度估计总体
1.为了从整体上更好地把握总体规律,我们还可以通过样本数据的众数、中位数、平均数估计总体的集中趋势,通过样本数据的方差或标准差估计总体的离散程度.
2.掌握样本数据的众数、中位数、平均数及方差的计算方法,提升数据分析和数学运算素养.
例3 (1)16名跳高运动员参加一项校际比赛,成绩(单位:m)分别为
1.70,1.65,1.68,1.69,1.72,1.59,1.60,1.67,1.74,1.78,1.55,1.56,1.64,1.76,1.75,1.79.
则比赛成绩的75%分位数是( )
A.1.755 B.1.75
C.1.745 D.1.74
(2)某班全体学生物理测试成绩(单位:分)的频率分布直方图如图所示,则估计该班物理测试成绩的众数、中位数、平均数分别是( )
A.70,70,70 B.70,70,68
C.70,68,70 D.68,70,70
(3)某电池厂有A,B两条生产线,现从A生产线中取出8件产品,测得它们的可充电次数的平均数为210,方差为4;从B生产线中取出12件产品,测得它们的可充电次数的平均数为200,方差为4.则这20件产品组成的总样本的方差为________.
反思感悟 通常我们用样本的平均数和方差(标准差)来近似代替总体的平均数和方差(标准差),呈现样本数据的集中趋势及波动大小,从而实现对总体的估计.
(1)一般情况下,需要将平均数和标准差结合,得到更多样本数据的信息,从而对总体作出较好的估计.因为平均数容易掩盖一些极端情况,使我们对总体作出片面的判断,而标准差较好地避免了极端情况.
(2)若两组数据的平均数差别很大,也可以只比较平均数,估计总体的平均水平,从而作出判断.
跟踪训练3 (1)(多选)某班级体温检测员对一周内甲、乙两名同学的体温进行了统计,其结果如图所示,则( )
A.甲同学体温的极差为0.4 ℃
B.乙同学体温的众数为36.4 ℃,中位数与平均数相等
C.乙同学的体温比甲同学的体温稳定
D.甲同学体温的第60百分位数为36.4 ℃
(2)某汽车租赁公司为了调查A型汽车与B型汽车的出租情况,现随机抽取这两种车各50辆,分别统计每辆车在某个星期内的出租天数,统计数据如下表:
A型汽车
出租天数 3 4 5 6 7
车辆数 3 30 5 7 5
B型汽车
出租天数 3 4 5 6 7
车辆数 10 10 15 10 5
①试根据上面的统计数据,判断这两种车在某个星期内的出租天数的方差的大小关系(只需写出结果);
②如果A型汽车与B型汽车每辆车每天出租获得的利润相同,该公司需要购买一辆汽车,请你根据所学的统计知识,给出建议应该购买哪一种车,并说明你的理由.
章末复习课
例1 D 跟踪训练1 (1)D (2)C
例2 解 (1)样本中男生人数是40,由抽样比例是1∶10可得高一年级男生人数是400,
男生“智力评分”的频率分布直方图如图所示.
(2)样本中“智力评分”在[165,175)内的频数为28,所以估计该校高一年级学生“智力评分”在[165,175)内的学生人数为28×10=280.
跟踪训练2 0.04 87.5
例3 (1)C
(2)B [由题意知众数为
=70;
因为(0.005+0.010)×20
=0.3<0.5,
(0.005+0.010+0.020)×20
=0.7>0.5,
所以中位数位于[60,80)中,
设中位数为x,则(0.005+0.010)×20+(x-60)×0.020=0.5,
解得x=70;
平均数为30×0.1+50×0.2+70×0.4+90×0.3=68.]
(3)28
解析 方法一 总样本的平均数
=×210+×200=204,
方差s2=[4+(210-204)2]+[4+(200-204)2]=28.
跟踪训练3 (1)ABC [对于A,甲同学体温的极差为
36.6-36.2=0.4(℃),故A正确;
对于B,乙同学体温为
36.4,36.3,36.5,36.4,36.4,36.3,36.5,其众数为36.4 ℃,中位数、平均数均为36.4 ℃,故B正确;
对于C,根据图中数据,甲同学体温的平均数为36.4 ℃,与乙同学体温的平均数相同,但甲同学的体温极差为0.4 ℃,大于乙同学的体温极差0.2 ℃,而且从图中容易看出乙同学的数据更集中,故乙同学的体温比甲同学的体温稳定,故C正确;
对于D,甲同学的体温从小到大排序为36.2,36.2,36.4,36.4,36.5,36.5,36.6,7×60%=4.2,故甲同学体温的第60百分位数为36.5 ℃,故D错误.]
(2)解 ①由数据的离散程度,可以看出B型汽车在某个星期内出租天数的方差较大.
②50辆A型汽车出租天数的平均数为A=
=4.62,
50辆B型汽车出租天数的平均数为
B=
=4.8,
方案一:A型汽车在某个星期内出租天数的平均数为4.62,B型汽车在某个星期内出租天数的平均数为4.8,选择B型汽车的出租车的利润较大,应该购买B型汽车.
方案二:A型汽车在某个星期内出租天数的平均数为4.62,B型汽车在某个星期内出租天数的平均数为4.8,而B型汽车出租天数的方差较大,所以应该购买A型汽车.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
