19.3课题学习选择方案练习题(含答案)2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 19.3课题学习选择方案练习题(含答案)2023-2024学年人教版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 00:00:00 | ||
图片预览


文档简介
19.3课题学习选择方案 练习题
一.选择题(共12小题)
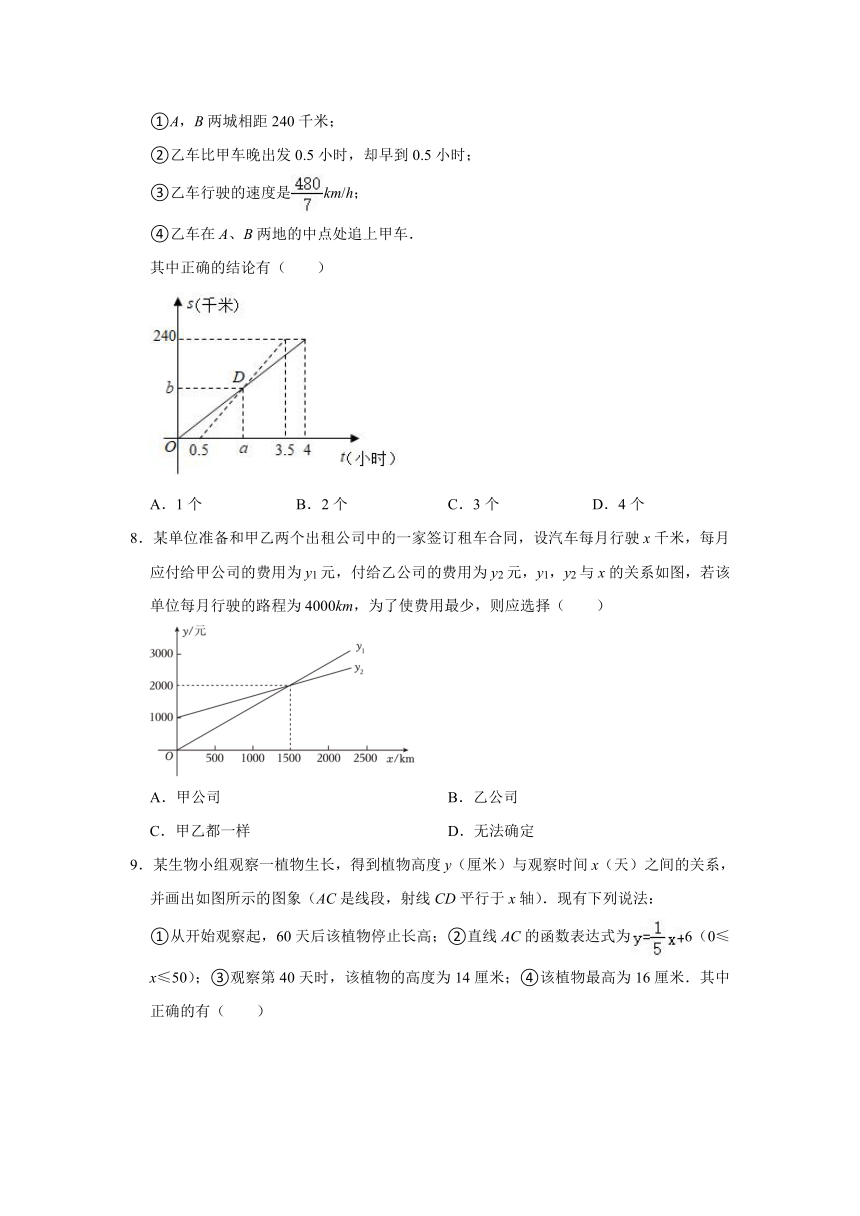
1.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20kg B.25kg C.28kg D.30kg
2.若等腰三角形的周长是20cm,则能反映这个等腰三角形的腰长y cm与底边长x cm的函数关系的图象是( )
A.B. C.D.
3.百货大楼进了一批花布,出售时要在进价(进货价格) 的基础上加一定的利润,其长度x与售价y如下表,下列用长度x表示售价y的关系式中,正确的是( )
长度x/m 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
4.在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,如图,折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
A.乙先出发的时间为0.5小时 B.甲的速度比乙的速度快
C.甲出发0.4小时后两车相遇 D.甲到B地比乙到A地迟5分钟
5.甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图,下列结论正确的有( )个
①A、B两城相距300千米;
②甲车比乙车早出发1小时,却晚到1小时;
③相遇时乙车行驶了2.5小时;
④当甲乙两车相距50千米时,t的值为或或或.
A.1 B.2 C.3 D.4
6.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5kg后,超过的部分价格优惠是打五折
D.若顾客采摘15kg草莓,那么到甲园比到乙园采摘更实惠
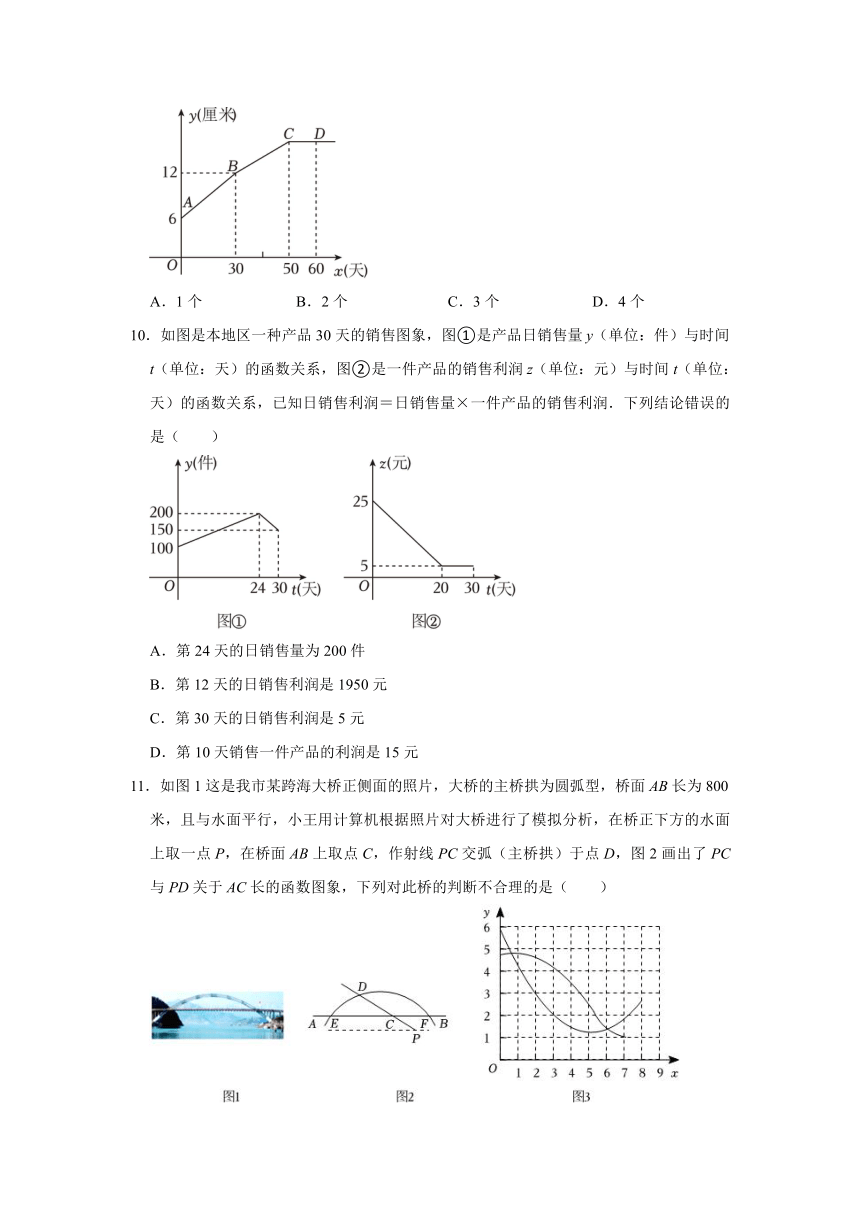
7.甲、乙两车将一批抗疫物资从A地运往B地,两车各自的速度都保持匀速行驶,甲、乙两车离A地的距离s(km)与甲车行驶时间t(h)之间的函数关系如图所示,则下列结论:
①A,B两城相距240千米;
②乙车比甲车晚出发0.5小时,却早到0.5小时;
③乙车行驶的速度是km/h;
④乙车在A、B两地的中点处追上甲车.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.某单位准备和甲乙两个出租公司中的一家签订租车合同,设汽车每月行驶x千米,每月应付给甲公司的费用为y1元,付给乙公司的费用为y2元,y1,y2与x的关系如图,若该单位每月行驶的路程为4000km,为了使费用最少,则应选择( )
A.甲公司 B.乙公司
C.甲乙都一样 D.无法确定
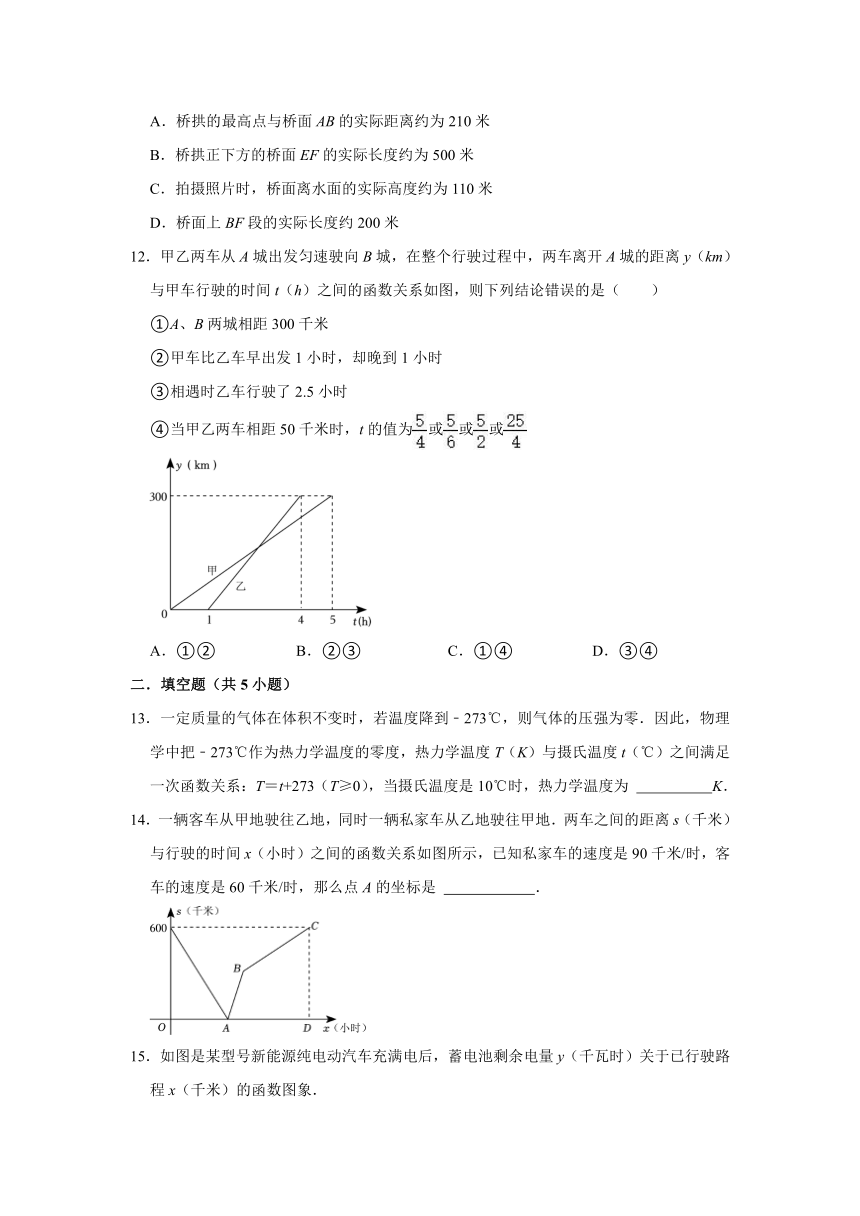
9.某生物小组观察一植物生长,得到植物高度y(厘米)与观察时间x(天)之间的关系,并画出如图所示的图象(AC是线段,射线CD平行于x轴).现有下列说法:
①从开始观察起,60天后该植物停止长高;②直线AC的函数表达式为6(0≤x≤50);③观察第40天时,该植物的高度为14厘米;④该植物最高为16厘米.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
A.第24天的日销售量为200件
B.第12天的日销售利润是1950元
C.第30天的日销售利润是5元
D.第10天销售一件产品的利润是15元
11.如图1这是我市某跨海大桥正侧面的照片,大桥的主桥拱为圆弧型,桥面AB长为800米,且与水面平行,小王用计算机根据照片对大桥进行了模拟分析,在桥正下方的水面上取一点P,在桥面AB上取点C,作射线PC交弧(主桥拱)于点D,图2画出了PC与PD关于AC长的函数图象,下列对此桥的判断不合理的是( )
A.桥拱的最高点与桥面AB的实际距离约为210米
B.桥拱正下方的桥面EF的实际长度约为500米
C.拍摄照片时,桥面离水面的实际高度约为110米
D.桥面上BF段的实际长度约200米
12.甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图,则下列结论错误的是( )
①A、B两城相距300千米
②甲车比乙车早出发1小时,却晚到1小时
③相遇时乙车行驶了2.5小时
④当甲乙两车相距50千米时,t的值为或或或
A.①② B.②③ C.①④ D.③④
二.填空题(共5小题)
13.一定质量的气体在体积不变时,若温度降到﹣273℃,则气体的压强为零.因此,物理学中把﹣273℃作为热力学温度的零度,热力学温度T(K)与摄氏温度t(℃)之间满足一次函数关系:T=t+273(T≥0),当摄氏温度是10℃时,热力学温度为 K.
14.一辆客车从甲地驶往乙地,同时一辆私家车从乙地驶往甲地.两车之间的距离s(千米)与行驶的时间x(小时)之间的函数关系如图所示,已知私家车的速度是90千米/时,客车的速度是60千米/时,那么点A的坐标是 .
15.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
①该汽车的蓄电池充满电时,电量是60千瓦时;
②蓄电池剩余电量为35千瓦时时汽车已行驶了150千米;
③当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时;
④25千瓦时的电量,汽车能行驶150km.
说法错误的是
16.货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为x(单位:h),货车、轿车与甲地的距离为y1(单位:km),y2(单位:km),图中的线段OA、折线BCDE分别表示y1,y2与x之间的函数关系.
(1)货车行驶的速度为 km/h;
(2)两车出发 h时,两车相距150km.
17.一直以来,人们力图探寻地球内部的奥秘,科学家做了大量的模拟实验后发现:地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可近似地表示为y=35x+20.当岩层的温度y(℃)达到720℃时,根据上述关系式,求该岩层所处的深度为 km.
三.解答题(共5小题)
18.蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.某景区为响应《关于推动露营旅游休闲健康有序发展的指导意见》精神,需要购买A,B两种型号的帐篷.已知购买A种帐篷2顶和B种帐篷4顶,共需5200元;购买A种帐篷3顶和B种帐篷1顶,共需2800元.
(1)求A种帐篷和B种帐篷的单价各是多少元?
(2)若该景区需要购买A,B两种型号的帐篷共20顶(两种型号的帐篷均需购买),其中B种帐篷数量不少于16顶,为使购买帐篷的总费用最低,应购买A种帐篷和B种帐篷各多少顶?购买帐篷的总费用最低为多少元?
19.书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某校准备在某超市为书法课购买一批毛笔和宣纸,已知毛笔每支的价格为5元,宣纸每张的价格为0.36元.该校准备购买毛笔50支,宣纸x张(x>200),该超市给出以下两种优惠方案,顾客只能选择其中一种方案.
方案A:购买一支毛笔,赠送一张宣纸;
方案B:购买的宣纸超出200张的部分打七五折,毛笔不打折.
设方案A所需的总费用为y1元,方案B所需的总费用为y2元.
(1)请分别求出y1,y2与x之间的函数关系式;
(2)该校选择哪种方案更划算?请说明理由.
20.某单位准备购买一种水果,现有甲、乙两家超市进行促销活动,该水果在两家超市的标价均为13元/千克.甲超市购买该水果的费用y(元)与该水果的质量x(千克)之间的关系如图所示;乙超市该水果在标价的基础上每千克直降3元.
(1)求y与x之间的函数表达式;
(2)现计划用290元购买该水果,选甲、乙哪家超市能购买该水果更多一些?
21.综合与探究
如图1,在平面直角坐标系中,直线l1:y=2x+6与x轴、y轴分别交于点A,B,直线l2经过点B,与x轴正半轴交于点C,且OC=OB.
(1)求A,B两点的坐标,并直接写出直线l2的函数表达式;
(2)如图2,点D是线段OB上的一个动点(不与点B和点O重合),设点D的纵坐标为n.
过点D作x轴的平行线,分别交直线l1,l2于点E,F.
①当n=2时,求线段EF的长;
②若点P是x轴上的一个动点,当△PEF是等腰直角三角形时,直接写出点P的坐标.
22.如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a,b满足+(a﹣4)2=0.
(1)a= ,b= ;
(2)如图1,若点C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(3)如图2,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过点D作DN⊥DM交x轴于点N,当点M在y轴正半轴上运动的过程中,式子S△BDM﹣S△ADN的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求出该式子的值.
参考答案
一.选择题(共12小题)
1--10ABBCB DCBCC 11--12AD
二.填空题(共5小题)
13.283
14.(4,0)
15.④.
16.(1)75;
(2)2.25或4.75
17.20
三.解答题(共5小题)
18.解:(1)设每顶A种型号帐篷m元,每顶B种型号帐篷n元,
根据题意得:,
解得:,
∴每顶A种型号帐篷600元,每顶B种型号帐篷1000元;
(2)设购买A种型号帐篷x顶,总费用为w元,则购买B种型号帐篷(20﹣x)顶,
∵B种帐篷数量不少于16顶
∴20﹣x≥16,
解得x≤4,
根据题意得:w=600x+1000(20﹣x)=﹣400x+20000,
∵﹣400<0,
∴w随x的增大而减小,
∴当x=4时,w取最小值,最小值为﹣400×4+20000=18400(元),
∴20﹣x=20﹣4=16,
答:购买A种型号帐篷4顶,购买B种型号帐篷16顶,总费用最低,最低总费用为18400元.
19.解:(1)由题意可得,
y1=5×50+0.36(x﹣50)=0.36x+232;
y2=5×50+0.36×200+0.36×(x﹣200)×0.75=0.27x+268;
(2)当0.36x+232=0.27x+268时,
解得x=400,
即当x=400时,选择两种方案一样划算;
当0.36x+232<0.27x+268时,
解得x<400,
即当200<x<400时,选择方案A划算;
当0.36x+232>0.27x+268时,
解得x>400,
即当x>400时,选择方案B划算;
答:当200<x<400时,选择方案A划算;当x=400时,选择两种方案一样划算;当x>400时,选择方案B划算.
20.解:(1)当0≤x≤5时,设y1与x之间的函数解析式为y1=kx(k≠0),
把(5,65)代入解析式得:5k=65,
解得k=13,
∴y1=13x;
当x>5时,设y1与x之间的函数解析式为y1=mx+n(m≠0),
把(5,65)和(10,110)代入解析式得,
解得,
∴y1=9x+20,
综上所述,y1与x之间的函数解析式为y1=;
(2)在甲商店购买:9x+20=290,
解得x=30,
∴在甲商店290元可以购买30千克水果;
在乙商店购买:10x=290,
解得x=29,
∴在乙商店290元可以购买29千克,
∵30>29,
∴在甲商店购买更多一些.
21.解:(1)∵直线l1:y=2x+6与x轴、y轴分别交于点A,B,
令x=0,则y=6,
∴B(0,6),
令y=0,则x=﹣3,
∴A(﹣3,0),
∵OC=OB,
∴点C的坐标为(6,0),
设直线l2的函数表达式为y=kx+b,
,
解得,
∴直线l2的函数表达式为y=﹣x+6;
(2)①设点D的纵坐标为n.
∵过点D作x轴的平行线,分别交直线l1,l2于点E,F.
∴点E的坐标为(﹣3,n),点F的坐标为(6﹣n,n),
当n=2时,点E的坐标为(﹣2,2),点F的坐标为(4,2),
∴线段EF的长为4+2=6;
②由①知点E的坐标为(﹣3,n),点F的坐标为(6﹣n,n),
当∠PEF=90°,EF=EP时,
∴6﹣n﹣+3=n,解得n=,
∴点E的坐标为(﹣,),
∴点P的坐标为(﹣,0);
当∠PFE=90°,EF=PF时,
∴6﹣n﹣+3=n,解得n=,
∴点F的坐标为(,),
∴点P的坐标为(,0);
当∠EPF=90°,PE=PF时,过点P作PH⊥EF于H,
∵△PEF是等腰直角三角形,
∴EH=FH,
∴PH=EH=FH=EF=(6﹣n﹣+3)=n,
∴n=,
∴点F的坐标为(,),
∴点P的坐标为(,0);
综上,点P的坐标为(﹣,0)或(,0)或(,0).
22.解:(1)∵+(a﹣4)2=0,且≥0,(a﹣4)2≥0,
∴a+b=0,a﹣4=0,
∴a=4,b=﹣4.
故答案为:4,﹣4;
(2)∵a=4,b=﹣4,则OA=OB=4.
∵AH⊥BC于H,
∴∠OAP+∠OPA=∠BPH+∠OBC=90°,
∴∠OAP=∠OBC,
在△OAP与△OBC中,
,
∴△OAP≌△OBC(ASA),
∴OP=OC=1,
则P(0,﹣1);
(3)S△BDM﹣S△ADN的值不发生改变.S△BDM﹣S△ADN=4.
连接OD,则OD⊥AB,∠BOD=∠AOD=45°,∠OAD=45°
∴OD=AD,
∴∠MDO=∠NDA=90°﹣∠MDA,
在△ODM与△ADN中,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△ADN,
∴S△BDM﹣S△ADN=S△BDM﹣S△ODM=S△BOD=S△AOB=×AO BO=××4×4=4.
一.选择题(共12小题)
1.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20kg B.25kg C.28kg D.30kg
2.若等腰三角形的周长是20cm,则能反映这个等腰三角形的腰长y cm与底边长x cm的函数关系的图象是( )
A.B. C.D.
3.百货大楼进了一批花布,出售时要在进价(进货价格) 的基础上加一定的利润,其长度x与售价y如下表,下列用长度x表示售价y的关系式中,正确的是( )
长度x/m 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
4.在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,如图,折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
A.乙先出发的时间为0.5小时 B.甲的速度比乙的速度快
C.甲出发0.4小时后两车相遇 D.甲到B地比乙到A地迟5分钟
5.甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图,下列结论正确的有( )个
①A、B两城相距300千米;
②甲车比乙车早出发1小时,却晚到1小时;
③相遇时乙车行驶了2.5小时;
④当甲乙两车相距50千米时,t的值为或或或.
A.1 B.2 C.3 D.4
6.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5kg后,超过的部分价格优惠是打五折
D.若顾客采摘15kg草莓,那么到甲园比到乙园采摘更实惠
7.甲、乙两车将一批抗疫物资从A地运往B地,两车各自的速度都保持匀速行驶,甲、乙两车离A地的距离s(km)与甲车行驶时间t(h)之间的函数关系如图所示,则下列结论:
①A,B两城相距240千米;
②乙车比甲车晚出发0.5小时,却早到0.5小时;
③乙车行驶的速度是km/h;
④乙车在A、B两地的中点处追上甲车.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.某单位准备和甲乙两个出租公司中的一家签订租车合同,设汽车每月行驶x千米,每月应付给甲公司的费用为y1元,付给乙公司的费用为y2元,y1,y2与x的关系如图,若该单位每月行驶的路程为4000km,为了使费用最少,则应选择( )
A.甲公司 B.乙公司
C.甲乙都一样 D.无法确定
9.某生物小组观察一植物生长,得到植物高度y(厘米)与观察时间x(天)之间的关系,并画出如图所示的图象(AC是线段,射线CD平行于x轴).现有下列说法:
①从开始观察起,60天后该植物停止长高;②直线AC的函数表达式为6(0≤x≤50);③观察第40天时,该植物的高度为14厘米;④该植物最高为16厘米.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
A.第24天的日销售量为200件
B.第12天的日销售利润是1950元
C.第30天的日销售利润是5元
D.第10天销售一件产品的利润是15元
11.如图1这是我市某跨海大桥正侧面的照片,大桥的主桥拱为圆弧型,桥面AB长为800米,且与水面平行,小王用计算机根据照片对大桥进行了模拟分析,在桥正下方的水面上取一点P,在桥面AB上取点C,作射线PC交弧(主桥拱)于点D,图2画出了PC与PD关于AC长的函数图象,下列对此桥的判断不合理的是( )
A.桥拱的最高点与桥面AB的实际距离约为210米
B.桥拱正下方的桥面EF的实际长度约为500米
C.拍摄照片时,桥面离水面的实际高度约为110米
D.桥面上BF段的实际长度约200米
12.甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图,则下列结论错误的是( )
①A、B两城相距300千米
②甲车比乙车早出发1小时,却晚到1小时
③相遇时乙车行驶了2.5小时
④当甲乙两车相距50千米时,t的值为或或或
A.①② B.②③ C.①④ D.③④
二.填空题(共5小题)
13.一定质量的气体在体积不变时,若温度降到﹣273℃,则气体的压强为零.因此,物理学中把﹣273℃作为热力学温度的零度,热力学温度T(K)与摄氏温度t(℃)之间满足一次函数关系:T=t+273(T≥0),当摄氏温度是10℃时,热力学温度为 K.
14.一辆客车从甲地驶往乙地,同时一辆私家车从乙地驶往甲地.两车之间的距离s(千米)与行驶的时间x(小时)之间的函数关系如图所示,已知私家车的速度是90千米/时,客车的速度是60千米/时,那么点A的坐标是 .
15.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
①该汽车的蓄电池充满电时,电量是60千瓦时;
②蓄电池剩余电量为35千瓦时时汽车已行驶了150千米;
③当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时;
④25千瓦时的电量,汽车能行驶150km.
说法错误的是
16.货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为x(单位:h),货车、轿车与甲地的距离为y1(单位:km),y2(单位:km),图中的线段OA、折线BCDE分别表示y1,y2与x之间的函数关系.
(1)货车行驶的速度为 km/h;
(2)两车出发 h时,两车相距150km.
17.一直以来,人们力图探寻地球内部的奥秘,科学家做了大量的模拟实验后发现:地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可近似地表示为y=35x+20.当岩层的温度y(℃)达到720℃时,根据上述关系式,求该岩层所处的深度为 km.
三.解答题(共5小题)
18.蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.某景区为响应《关于推动露营旅游休闲健康有序发展的指导意见》精神,需要购买A,B两种型号的帐篷.已知购买A种帐篷2顶和B种帐篷4顶,共需5200元;购买A种帐篷3顶和B种帐篷1顶,共需2800元.
(1)求A种帐篷和B种帐篷的单价各是多少元?
(2)若该景区需要购买A,B两种型号的帐篷共20顶(两种型号的帐篷均需购买),其中B种帐篷数量不少于16顶,为使购买帐篷的总费用最低,应购买A种帐篷和B种帐篷各多少顶?购买帐篷的总费用最低为多少元?
19.书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某校准备在某超市为书法课购买一批毛笔和宣纸,已知毛笔每支的价格为5元,宣纸每张的价格为0.36元.该校准备购买毛笔50支,宣纸x张(x>200),该超市给出以下两种优惠方案,顾客只能选择其中一种方案.
方案A:购买一支毛笔,赠送一张宣纸;
方案B:购买的宣纸超出200张的部分打七五折,毛笔不打折.
设方案A所需的总费用为y1元,方案B所需的总费用为y2元.
(1)请分别求出y1,y2与x之间的函数关系式;
(2)该校选择哪种方案更划算?请说明理由.
20.某单位准备购买一种水果,现有甲、乙两家超市进行促销活动,该水果在两家超市的标价均为13元/千克.甲超市购买该水果的费用y(元)与该水果的质量x(千克)之间的关系如图所示;乙超市该水果在标价的基础上每千克直降3元.
(1)求y与x之间的函数表达式;
(2)现计划用290元购买该水果,选甲、乙哪家超市能购买该水果更多一些?
21.综合与探究
如图1,在平面直角坐标系中,直线l1:y=2x+6与x轴、y轴分别交于点A,B,直线l2经过点B,与x轴正半轴交于点C,且OC=OB.
(1)求A,B两点的坐标,并直接写出直线l2的函数表达式;
(2)如图2,点D是线段OB上的一个动点(不与点B和点O重合),设点D的纵坐标为n.
过点D作x轴的平行线,分别交直线l1,l2于点E,F.
①当n=2时,求线段EF的长;
②若点P是x轴上的一个动点,当△PEF是等腰直角三角形时,直接写出点P的坐标.
22.如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a,b满足+(a﹣4)2=0.
(1)a= ,b= ;
(2)如图1,若点C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(3)如图2,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过点D作DN⊥DM交x轴于点N,当点M在y轴正半轴上运动的过程中,式子S△BDM﹣S△ADN的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求出该式子的值.
参考答案
一.选择题(共12小题)
1--10ABBCB DCBCC 11--12AD
二.填空题(共5小题)
13.283
14.(4,0)
15.④.
16.(1)75;
(2)2.25或4.75
17.20
三.解答题(共5小题)
18.解:(1)设每顶A种型号帐篷m元,每顶B种型号帐篷n元,
根据题意得:,
解得:,
∴每顶A种型号帐篷600元,每顶B种型号帐篷1000元;
(2)设购买A种型号帐篷x顶,总费用为w元,则购买B种型号帐篷(20﹣x)顶,
∵B种帐篷数量不少于16顶
∴20﹣x≥16,
解得x≤4,
根据题意得:w=600x+1000(20﹣x)=﹣400x+20000,
∵﹣400<0,
∴w随x的增大而减小,
∴当x=4时,w取最小值,最小值为﹣400×4+20000=18400(元),
∴20﹣x=20﹣4=16,
答:购买A种型号帐篷4顶,购买B种型号帐篷16顶,总费用最低,最低总费用为18400元.
19.解:(1)由题意可得,
y1=5×50+0.36(x﹣50)=0.36x+232;
y2=5×50+0.36×200+0.36×(x﹣200)×0.75=0.27x+268;
(2)当0.36x+232=0.27x+268时,
解得x=400,
即当x=400时,选择两种方案一样划算;
当0.36x+232<0.27x+268时,
解得x<400,
即当200<x<400时,选择方案A划算;
当0.36x+232>0.27x+268时,
解得x>400,
即当x>400时,选择方案B划算;
答:当200<x<400时,选择方案A划算;当x=400时,选择两种方案一样划算;当x>400时,选择方案B划算.
20.解:(1)当0≤x≤5时,设y1与x之间的函数解析式为y1=kx(k≠0),
把(5,65)代入解析式得:5k=65,
解得k=13,
∴y1=13x;
当x>5时,设y1与x之间的函数解析式为y1=mx+n(m≠0),
把(5,65)和(10,110)代入解析式得,
解得,
∴y1=9x+20,
综上所述,y1与x之间的函数解析式为y1=;
(2)在甲商店购买:9x+20=290,
解得x=30,
∴在甲商店290元可以购买30千克水果;
在乙商店购买:10x=290,
解得x=29,
∴在乙商店290元可以购买29千克,
∵30>29,
∴在甲商店购买更多一些.
21.解:(1)∵直线l1:y=2x+6与x轴、y轴分别交于点A,B,
令x=0,则y=6,
∴B(0,6),
令y=0,则x=﹣3,
∴A(﹣3,0),
∵OC=OB,
∴点C的坐标为(6,0),
设直线l2的函数表达式为y=kx+b,
,
解得,
∴直线l2的函数表达式为y=﹣x+6;
(2)①设点D的纵坐标为n.
∵过点D作x轴的平行线,分别交直线l1,l2于点E,F.
∴点E的坐标为(﹣3,n),点F的坐标为(6﹣n,n),
当n=2时,点E的坐标为(﹣2,2),点F的坐标为(4,2),
∴线段EF的长为4+2=6;
②由①知点E的坐标为(﹣3,n),点F的坐标为(6﹣n,n),
当∠PEF=90°,EF=EP时,
∴6﹣n﹣+3=n,解得n=,
∴点E的坐标为(﹣,),
∴点P的坐标为(﹣,0);
当∠PFE=90°,EF=PF时,
∴6﹣n﹣+3=n,解得n=,
∴点F的坐标为(,),
∴点P的坐标为(,0);
当∠EPF=90°,PE=PF时,过点P作PH⊥EF于H,
∵△PEF是等腰直角三角形,
∴EH=FH,
∴PH=EH=FH=EF=(6﹣n﹣+3)=n,
∴n=,
∴点F的坐标为(,),
∴点P的坐标为(,0);
综上,点P的坐标为(﹣,0)或(,0)或(,0).
22.解:(1)∵+(a﹣4)2=0,且≥0,(a﹣4)2≥0,
∴a+b=0,a﹣4=0,
∴a=4,b=﹣4.
故答案为:4,﹣4;
(2)∵a=4,b=﹣4,则OA=OB=4.
∵AH⊥BC于H,
∴∠OAP+∠OPA=∠BPH+∠OBC=90°,
∴∠OAP=∠OBC,
在△OAP与△OBC中,
,
∴△OAP≌△OBC(ASA),
∴OP=OC=1,
则P(0,﹣1);
(3)S△BDM﹣S△ADN的值不发生改变.S△BDM﹣S△ADN=4.
连接OD,则OD⊥AB,∠BOD=∠AOD=45°,∠OAD=45°
∴OD=AD,
∴∠MDO=∠NDA=90°﹣∠MDA,
在△ODM与△ADN中,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△ADN,
∴S△BDM﹣S△ADN=S△BDM﹣S△ODM=S△BOD=S△AOB=×AO BO=××4×4=4.
