河北省保定市高阳中学2014-2015学年高一下学期第十次周练数学试题
文档属性
| 名称 | 河北省保定市高阳中学2014-2015学年高一下学期第十次周练数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 130.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-27 00:00:00 | ||
图片预览


文档简介
高一数学周练六十九
1.若直线m不平行于平面α,且m α,则下列结论成立的是( )
A.α内所有直线与m异面
B.α内存在唯一的直线与m平行
C.α内的直线与m相交
D.α内不存在与m平行的直线
2.设AB,BC,CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是( )
A.平行 B.相交
C.平行或相交 D.AC在此平面内
3.如果两直线a∥b,且a∥平面α,那么b与α的位置关系( )
A.相交 B.b∥α
C.b α D.b∥α或b α
4.已知直线a⊥b,a∥平面α,则直线b与平面α的位置关系是( )
A.b∥α B.b α
C. b与α相交 D.以上都有可能
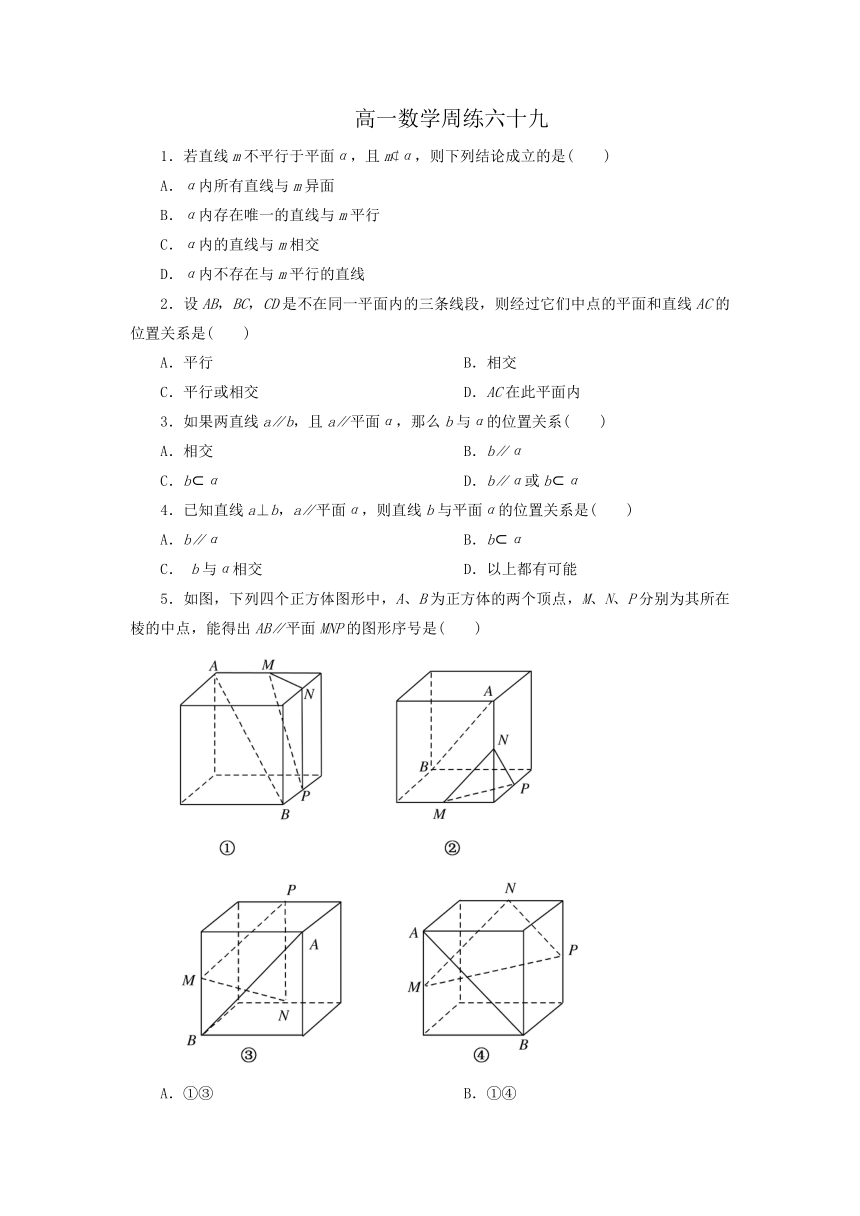
5.如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是( )
A.①③ B.①④
C.②③ D.②④
6.如图,在长方体ABCD-A1B1C1D1的面中:
(1)与直线AB平行的平面有________.
(2)与直线AA1平行的平面有________.
(3)若E为A1B1的中点,则直线AE与平面BB1C1C的关系是________.
7.已知不重合的直线a,b和平面β.
①若a∥β,b β,则a∥b;②若a∥β ( http: / / www.21cnjy.com ),b∥β,则a∥b;③若a∥b,b β,则a∥β;④若a∥b,a∥β,则b∥β或b β,其中正确命题的序号是________.
8.已知E,F,G,M分别是四面体的棱AD,CD,BD,BC的中点.
求证:AM∥平面EFG.
9.如图,在底面为平行四边形的四棱锥P-ABCD中,点E是PD的中点,求证:PB∥平面AEC.
10.如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
(1)求证:PQ∥平面DCC1D1;
(2)求PQ的长;
(3)求证:EF∥平面BB1D1D.
答案:
1. D
2. A
3. D
4. D
5. B
6. (1)平面A1B1C1D1,平面CC1D1D
(2)平面BB1C1C,平面CC1D1D
(3)相交
7.④
8.
如图所示,连接MD交GF于N,连接EN.
∵GF为△BCD的中位线,
∴N为MD的中点.
∴EN为△AMD的中位线.
∴EN∥AM.
∵AM 平面EFG,EN 平面EFG,
∴AM∥平面EFG.
9.连接BD与AC相交于O,连接EO,AE,
∵ABCD为平行四边形,
∴O是BD的中点.
又E为PD的中点,
∴EO∥PB.
∵PB 平面AEC,EO 平面AEC,
∴PB∥平面AEC.
10. (1)证明:连接D1C,
∵P,Q分别为AD1,AC的中点,
∴PQ綊D1C.
∵PQ 面DCC1D1,
D1C 面DCC1D1,
∴PQ∥面DCC1D1.
(2)∵D1C=a,
∴PQ=D1C=a.
(3)证明:取B1D1的中点Q1,连接Q1F,Q1B.
∵F为D1C1的中点,Q1F綊B1C1綊BE,
∴四边形Q1FEB为平行四边形,EF∥Q1B.
∴EF 面BB1D1D,Q1B 面BB1D1D.
∴EF∥面BB1D1D.
1.若直线m不平行于平面α,且m α,则下列结论成立的是( )
A.α内所有直线与m异面
B.α内存在唯一的直线与m平行
C.α内的直线与m相交
D.α内不存在与m平行的直线
2.设AB,BC,CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是( )
A.平行 B.相交
C.平行或相交 D.AC在此平面内
3.如果两直线a∥b,且a∥平面α,那么b与α的位置关系( )
A.相交 B.b∥α
C.b α D.b∥α或b α
4.已知直线a⊥b,a∥平面α,则直线b与平面α的位置关系是( )
A.b∥α B.b α
C. b与α相交 D.以上都有可能
5.如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是( )
A.①③ B.①④
C.②③ D.②④
6.如图,在长方体ABCD-A1B1C1D1的面中:
(1)与直线AB平行的平面有________.
(2)与直线AA1平行的平面有________.
(3)若E为A1B1的中点,则直线AE与平面BB1C1C的关系是________.
7.已知不重合的直线a,b和平面β.
①若a∥β,b β,则a∥b;②若a∥β ( http: / / www.21cnjy.com ),b∥β,则a∥b;③若a∥b,b β,则a∥β;④若a∥b,a∥β,则b∥β或b β,其中正确命题的序号是________.
8.已知E,F,G,M分别是四面体的棱AD,CD,BD,BC的中点.
求证:AM∥平面EFG.
9.如图,在底面为平行四边形的四棱锥P-ABCD中,点E是PD的中点,求证:PB∥平面AEC.
10.如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
(1)求证:PQ∥平面DCC1D1;
(2)求PQ的长;
(3)求证:EF∥平面BB1D1D.
答案:
1. D
2. A
3. D
4. D
5. B
6. (1)平面A1B1C1D1,平面CC1D1D
(2)平面BB1C1C,平面CC1D1D
(3)相交
7.④
8.
如图所示,连接MD交GF于N,连接EN.
∵GF为△BCD的中位线,
∴N为MD的中点.
∴EN为△AMD的中位线.
∴EN∥AM.
∵AM 平面EFG,EN 平面EFG,
∴AM∥平面EFG.
9.连接BD与AC相交于O,连接EO,AE,
∵ABCD为平行四边形,
∴O是BD的中点.
又E为PD的中点,
∴EO∥PB.
∵PB 平面AEC,EO 平面AEC,
∴PB∥平面AEC.
10. (1)证明:连接D1C,
∵P,Q分别为AD1,AC的中点,
∴PQ綊D1C.
∵PQ 面DCC1D1,
D1C 面DCC1D1,
∴PQ∥面DCC1D1.
(2)∵D1C=a,
∴PQ=D1C=a.
(3)证明:取B1D1的中点Q1,连接Q1F,Q1B.
∵F为D1C1的中点,Q1F綊B1C1綊BE,
∴四边形Q1FEB为平行四边形,EF∥Q1B.
∴EF 面BB1D1D,Q1B 面BB1D1D.
∴EF∥面BB1D1D.
同课章节目录
