解直角三角形的应用复习(广东省中山市)
文档属性
| 名称 | 解直角三角形的应用复习(广东省中山市) |  | |
| 格式 | rar | ||
| 文件大小 | 184.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-11 18:46:00 | ||
图片预览


文档简介
课件11张PPT。解直角三角形的应用复习(1) 如图:为测得一河两岸相对两电线杆A、B间的距离,在距离A点15米的C处(AC⊥AB)测得∠ACB=50o,则A、B间的距离应为( )
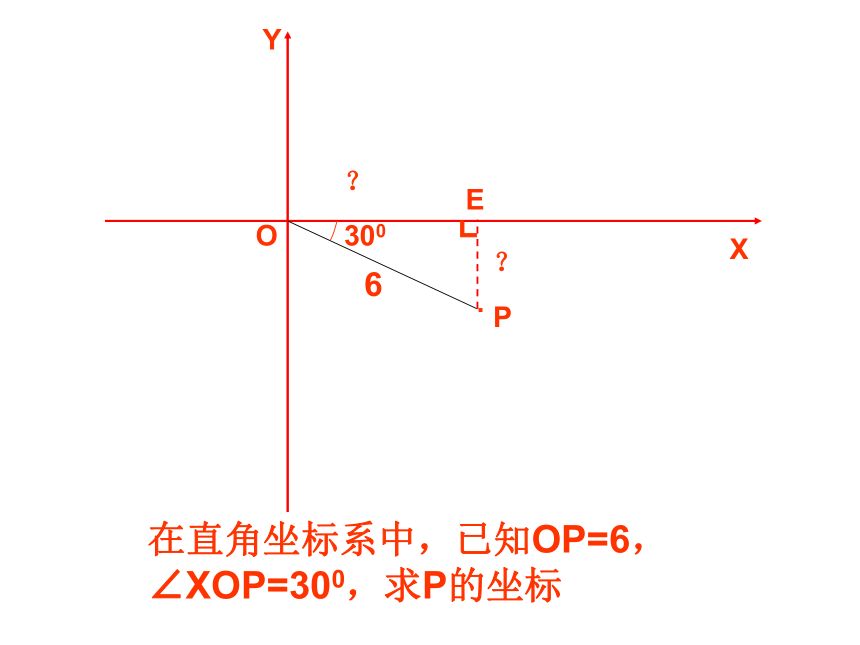
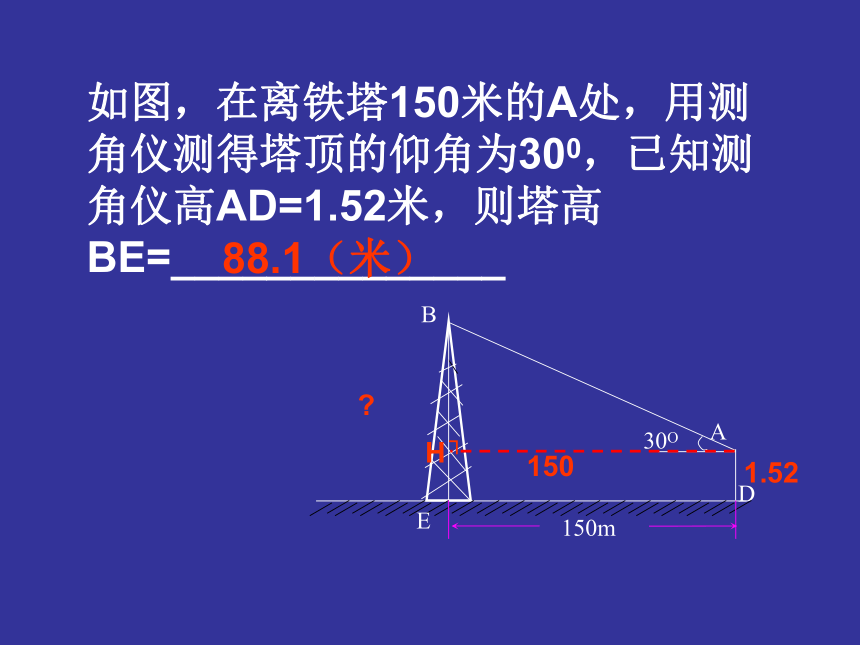
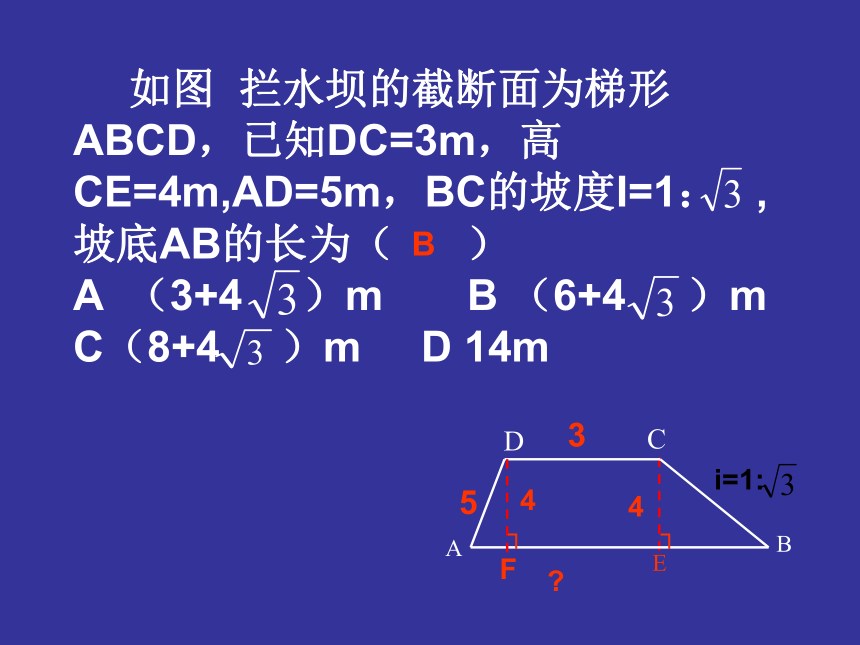
A 15sin50o米 B 15cos50o米 C 15tan50o米 D 15cot50o米C基础训练 ?┛50015XYOP.在直角坐标系中,已知OP=6,∠XOP=300,求P的坐标6300E┗??如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为300,已知测角仪高AD=1.52米,则塔高BE=______________ D30O150mABE88.1(米)┐H1.52?150BABCDE┐┐F345 i=1:4?
如图,灯塔A周围1000米水域内有礁石,一舰艇由西向东航行,在O处测得灯塔A在北偏东74 度方向线上。这时,O、A相距4200米,如果不改变航向,此舰艇是否有触礁的危险?北C7404200┏? 某学校把一块形状近似远直角的废地开辟为生物园,如图5所示,∠ACB=90o,BC=60米,∠A=36 o。
⑴ 若入口E在边AB上,且与A、B等距离,请你在图中画出入口E到C点的最短路线,并求出最短路线CE的长(保留整数);
⑵ 若线段CD是一条水渠,并且D点在边AB上,已知水渠造价为50元/米,水渠路线应如何设计才能使造价最低,请你画出水渠路线,并求出最低造价。┐BE技能与方法探究问题:
(1)你能说出最短路线是CE的理由吗?
经观察CE是Rt△ABC 斜边上的________,只要在Rt△ABC 中选用合适的关系式,求出边_________就可以。
(2)为什么说垂线段CD的长度是造价最低吗?┐ACBE D中线AB(1)最短路线如图所示,据题意,CE是Rt△ABC斜边上的中线,在Rt△ABC中,∠ACB=90o
∵sin36o= ∴AB= ≈102(米)∴CE= AB=51(米)解:(2)若要水渠造价最低,则水渠应与AB垂直,如图CD⊥AB
在Rt△ABC中, ∠ B=90o-36o=54o
∵Sin54o= ∴ CD=60× sin54o ≈ 48.54(米)
∴ 造价=50CD=50×48.54=2427(元)拓展与提高 如图:为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60 o,∠ACB=45 o,量得BC长为30米。求河的宽度(精确到1米) Goodbye本课到此结束
A 15sin50o米 B 15cos50o米 C 15tan50o米 D 15cot50o米C基础训练 ?┛50015XYOP.在直角坐标系中,已知OP=6,∠XOP=300,求P的坐标6300E┗??如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为300,已知测角仪高AD=1.52米,则塔高BE=______________ D30O150mABE88.1(米)┐H1.52?150BABCDE┐┐F345 i=1:4?
如图,灯塔A周围1000米水域内有礁石,一舰艇由西向东航行,在O处测得灯塔A在北偏东74 度方向线上。这时,O、A相距4200米,如果不改变航向,此舰艇是否有触礁的危险?北C7404200┏? 某学校把一块形状近似远直角的废地开辟为生物园,如图5所示,∠ACB=90o,BC=60米,∠A=36 o。
⑴ 若入口E在边AB上,且与A、B等距离,请你在图中画出入口E到C点的最短路线,并求出最短路线CE的长(保留整数);
⑵ 若线段CD是一条水渠,并且D点在边AB上,已知水渠造价为50元/米,水渠路线应如何设计才能使造价最低,请你画出水渠路线,并求出最低造价。┐BE技能与方法探究问题:
(1)你能说出最短路线是CE的理由吗?
经观察CE是Rt△ABC 斜边上的________,只要在Rt△ABC 中选用合适的关系式,求出边_________就可以。
(2)为什么说垂线段CD的长度是造价最低吗?┐ACBE D中线AB(1)最短路线如图所示,据题意,CE是Rt△ABC斜边上的中线,在Rt△ABC中,∠ACB=90o
∵sin36o= ∴AB= ≈102(米)∴CE= AB=51(米)解:(2)若要水渠造价最低,则水渠应与AB垂直,如图CD⊥AB
在Rt△ABC中, ∠ B=90o-36o=54o
∵Sin54o= ∴ CD=60× sin54o ≈ 48.54(米)
∴ 造价=50CD=50×48.54=2427(元)拓展与提高 如图:为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60 o,∠ACB=45 o,量得BC长为30米。求河的宽度(精确到1米) Goodbye本课到此结束
