相似三角形复习2(广东省中山市)
图片预览




文档简介
课件12张PPT。相似三角形复习2相似三角形的判定:(1)定义法:三角对应相等,三边对应成比例的两个三角形相似.
(4)三边对应成比例的两个三角形相似.
(3)两边对应成比例且夹角相等的两个三角形相似.
(2)两角对应相等的两个三角形相似.
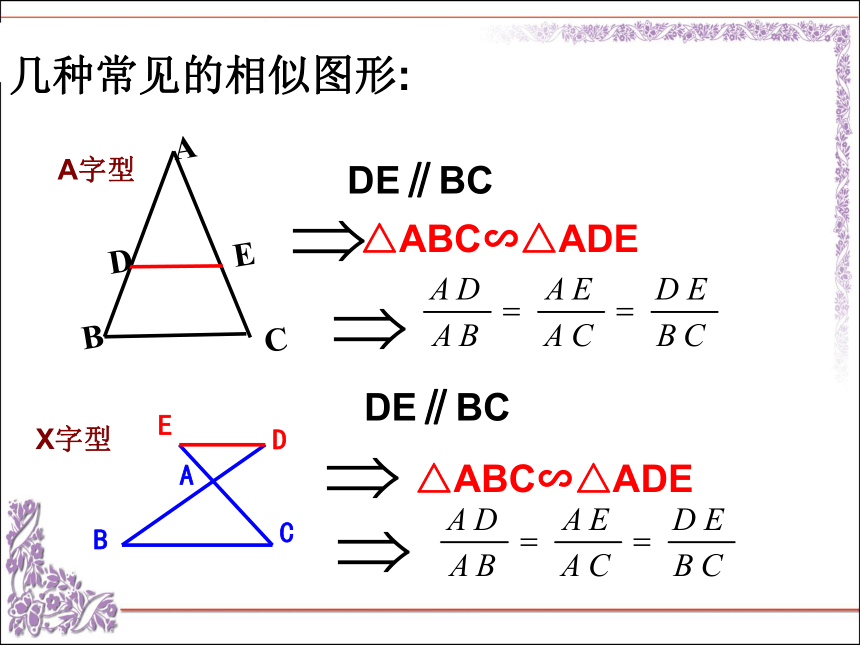
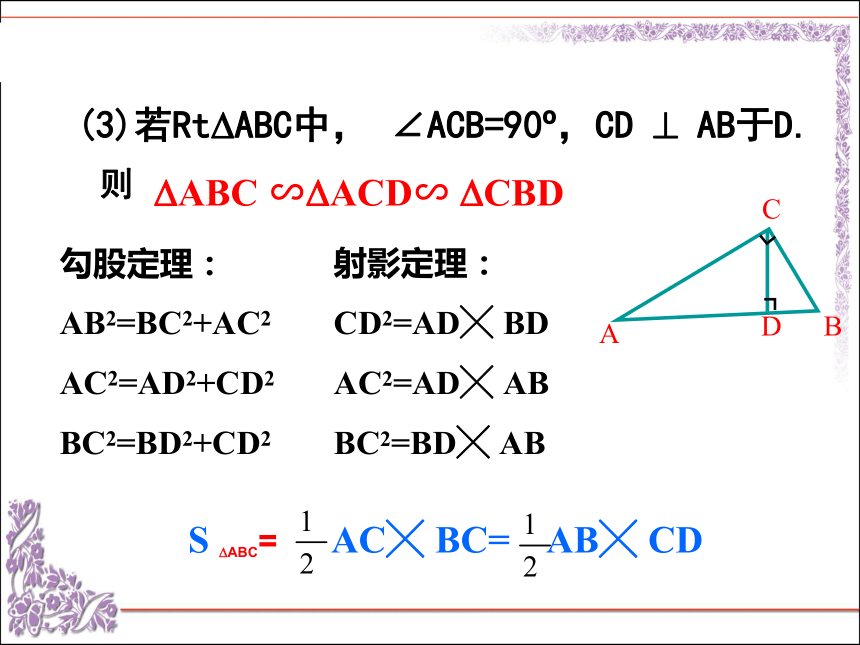
(3)周长的比等于相似比;(4)面积的比等于相似比的平方。(1)对应角相等,对应边成比例;相似三角形的性质:(2)对应线段(高、中线、角平分线)的比等于相似比;几种常见的相似图形:DE∥BC△ABC∽△ADEDE∥BC△ABC∽△ADEA字型X字型(3)若Rt?ABC中, ∠ACB=90o,CD ? AB于D.射影定理:
CD2=AD╳ BD
AC2=AD╳ AB
BC2=BD╳ AB勾股定理:
AB2=BC2+AC2
AC2=AD2+CD2
BC2=BD2+CD2
S ?ABC= AC╳ BC= AB╳ CD则?ABC ∽?ACD∽ ?CBD1、已知3:X=4:12,则X= 做一做2、已知:△ABC∽△DEF,相似比为2,那么他们的周长比为 ,面积比为 。3、如图(3),DE∥AB,则△ ∽△ ,有 ,若DE=3cm,BE=2cm,CE=4cm 则AB= 924ABCDECBC4.5做一做4、如图(4),DE∥BC,则△ ABC ∽△ ,若AE=6,AB=2,AC=1,则CD= 5、如图(5),P是△ ABC 中AB边上的一点,要使△ACP ∽△ABC需添加一个条件为 。 AED4∠ACP= ∠B或∠APC= ∠ACB或AB/AC=AC/APRt △ABC的斜边AB上有一动点P(不与点A、B重合 ),过P点作直线截△ABC,使截得的三角形与△ABC相似 ,则满足这样条件的直线共有多少条,请你画出来。 牛刀小试DEF渐入佳境 例1.在直角坐标系中,AB=2,OA=7,OC=3, AB⊥X轴于点A,C在y轴上,如果点P在线段OA上运动(点P不与O、A点重合) ,使得以P、A、B为顶点的三角形与以P、O、C为顶点的三角形相似,则点P的坐标是多少? 例2:直角三角形铁片ABC的两条直角边AB、BC的长分别是3和4,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案,甲设计方案如图1,乙设计方案如图2。你认为哪位同学设计的方案较好?
试说明理由。(加工损耗忽略不计 )图1图2图 1图 2例2变式: (1)若改为加工成一个面积最大的矩形桌面,其他条件不变,结果又怎么样? (2)矩形的面积可以变化,我们想到用什么表示?
(3)若在图1中面积设为y,其中一边设为x,怎么建立函数求出面积最大的矩形?
(4)三边对应成比例的两个三角形相似.
(3)两边对应成比例且夹角相等的两个三角形相似.
(2)两角对应相等的两个三角形相似.
(3)周长的比等于相似比;(4)面积的比等于相似比的平方。(1)对应角相等,对应边成比例;相似三角形的性质:(2)对应线段(高、中线、角平分线)的比等于相似比;几种常见的相似图形:DE∥BC△ABC∽△ADEDE∥BC△ABC∽△ADEA字型X字型(3)若Rt?ABC中, ∠ACB=90o,CD ? AB于D.射影定理:
CD2=AD╳ BD
AC2=AD╳ AB
BC2=BD╳ AB勾股定理:
AB2=BC2+AC2
AC2=AD2+CD2
BC2=BD2+CD2
S ?ABC= AC╳ BC= AB╳ CD则?ABC ∽?ACD∽ ?CBD1、已知3:X=4:12,则X= 做一做2、已知:△ABC∽△DEF,相似比为2,那么他们的周长比为 ,面积比为 。3、如图(3),DE∥AB,则△ ∽△ ,有 ,若DE=3cm,BE=2cm,CE=4cm 则AB= 924ABCDECBC4.5做一做4、如图(4),DE∥BC,则△ ABC ∽△ ,若AE=6,AB=2,AC=1,则CD= 5、如图(5),P是△ ABC 中AB边上的一点,要使△ACP ∽△ABC需添加一个条件为 。 AED4∠ACP= ∠B或∠APC= ∠ACB或AB/AC=AC/APRt △ABC的斜边AB上有一动点P(不与点A、B重合 ),过P点作直线截△ABC,使截得的三角形与△ABC相似 ,则满足这样条件的直线共有多少条,请你画出来。 牛刀小试DEF渐入佳境 例1.在直角坐标系中,AB=2,OA=7,OC=3, AB⊥X轴于点A,C在y轴上,如果点P在线段OA上运动(点P不与O、A点重合) ,使得以P、A、B为顶点的三角形与以P、O、C为顶点的三角形相似,则点P的坐标是多少? 例2:直角三角形铁片ABC的两条直角边AB、BC的长分别是3和4,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案,甲设计方案如图1,乙设计方案如图2。你认为哪位同学设计的方案较好?
试说明理由。(加工损耗忽略不计 )图1图2图 1图 2例2变式: (1)若改为加工成一个面积最大的矩形桌面,其他条件不变,结果又怎么样? (2)矩形的面积可以变化,我们想到用什么表示?
(3)若在图1中面积设为y,其中一边设为x,怎么建立函数求出面积最大的矩形?
