数学人教A版(2019)选择性必修第一册2.2.1直线的点斜式方程(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.1直线的点斜式方程(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 23:34:23 | ||
图片预览





文档简介
(共19张PPT)
直线的点斜式方程
1、理解直线方程的点斜式、斜截式的形式特点和适用范围;
(重点)
2、能正确利用直线的点斜式、斜截式公式求直线方程;
(难点)
3、体会直线的斜截式方程与一次函数的关系;
4、会利用直线方程判断直线平行或垂直。
学习目标
答:(1)已知两点可以确定一条直线。
问:在平面直角坐标系内如何确定一条直线呢?
(2)已知直线上的一点和这条直线的一个方 向(斜率或倾斜角)可以确定一条直线。
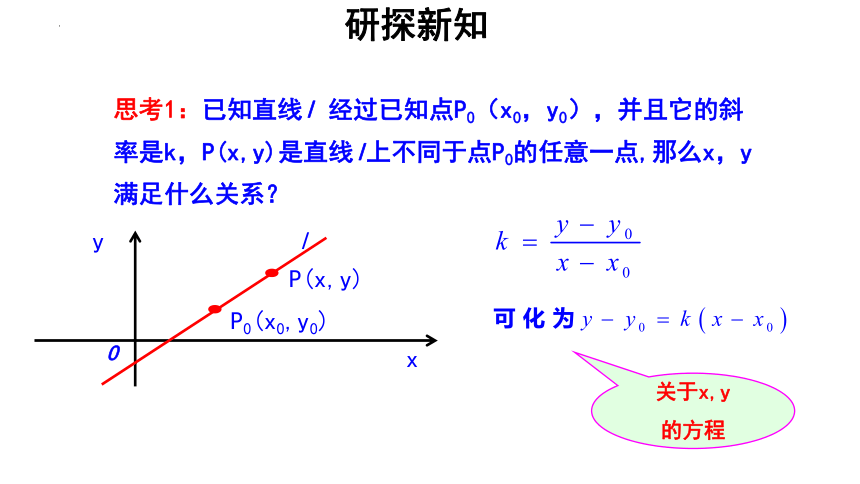
斜率公式:
(x1≠x2)
研探新知
思考1:已知直线l 经过已知点P0(x0,y0),并且它的斜率是k,P(x,y)是直线l上不同于点P0的任意一点,那么x,y满足什么关系?
x
y
O
P(x,y)
l
P0(x0,y0)
关于x,y
的方程
研探新知
思考2: 那么直线l上每一点的坐标都满足
这个方程吗
由推导过程知满足
P0(x0,y0)
满足方程
研探新知
思考3:满足方程y-y0=k(x-x0)的所有点P(x,y)是否都在直线l上 为什么?
研探新知
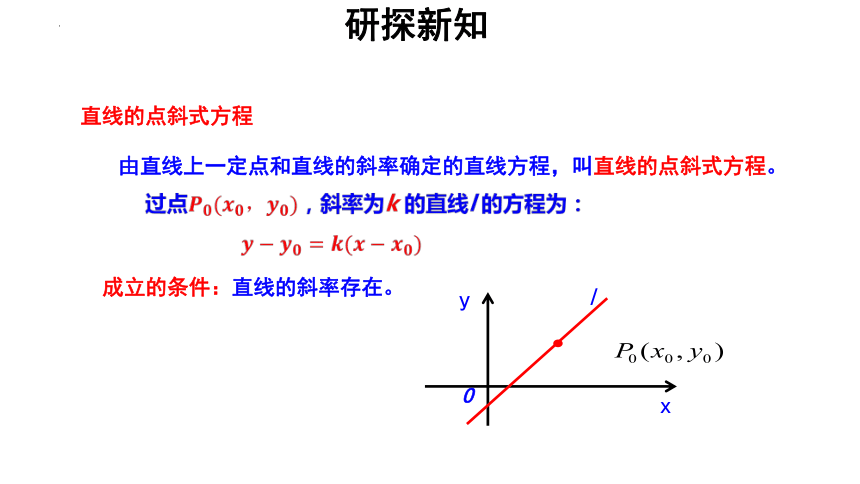
由直线上一定点和直线的斜率确定的直线方程,叫直线的点斜式方程。
直线的点斜式方程
成立的条件:直线的斜率存在。
x
y
O
l
研探新知
思考4:当直线l 的倾斜角是0°时,直线l 的方程是什么?
x
O
y
思考5:已知直线l 经过已知点P0(x0,y0),且它的斜率不存在,直线l的方程是什么?
x
y
O
研探新知
思考6:x轴、y轴所在直线的方程分别是什么?
y=0
x=0
x
O
y
研探新知
例1 直线l 经过点P0(-2,3),且倾斜角α=45°,求直线l 的点斜式方程,并画出直线l。
解:这条直线经过点P0(-2,3),
斜率k=tan45°=1
代入点斜式方程得
y-3=x+2
O
x
y
P0
5
-5
l
例题详解
思考7:已知直线l 的斜率是k,与y轴的交点是P(0,b),求直线方程。
代入点斜式方程得,
即y= kx+b
O
x
y
直线l 的方程:y-b=k(x-0),
P(0,b)
点斜式的特例
研探新知
上述方程是由直线的斜率k与它在y轴上的截距b确定,所以方程叫做直线的斜截式方程,简称斜截式。
y=kx+b
斜截式方程:
成立的条件:直线的斜率和在y轴上的截距存在。
O
x
y
b
斜率
在y轴上的截距
我们把直线l 与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距,
研探新知
思考8:方程y=kx+b与我们学过的一次函数表达式类似,我们知道一次函数的图像是一条直线,你如何从直线方程的角度认识一次函数y=kx+b?一次函数k和b的几何意义是什么?你能说出一次函数y=2x-1,y=3x,y=-x+3的图象的特点吗?
y=2x-1的斜率为2,在y轴上的截距为-1;
y=3x的斜率为3,在y轴上的截距为0;
y=-x+3的斜率为-1,在y轴上的截距为3。
研探新知
思考9:若直线l 的斜率为k,在x轴上的截距为a,则直线l 的方程是什么?
y=k(x-a)
思考10:如何求直线y-y0=k(x-x0)在x轴、y轴上的截距?
令y=0, 可求出直线在x轴上的截距;
令x=0,可求出直线在y轴上的截距.
研探新知
x
y
O
解:
例2
例题详解
课堂训练
2.填空题:
(1)已知直线的点斜式式方程是y-2=x-1,那么此直线的斜率是 ,倾斜角是 ;
(2)已知直线的点斜式方程是y+2= (x+1),那么此直线的斜率是 ,倾斜角是 。
3.写出下列直线的斜截式方程:
课堂训练
2.斜截式方程 是点斜式的一种特
殊情况
1.直线的点斜式方程
在直线斜率存在时才能应用
在直线斜率存在,及在y轴上截距存在时才能应用,理解k,b的几何意义
3.根据方程判断平行或垂直。
课堂小结
再见
直线的点斜式方程
1、理解直线方程的点斜式、斜截式的形式特点和适用范围;
(重点)
2、能正确利用直线的点斜式、斜截式公式求直线方程;
(难点)
3、体会直线的斜截式方程与一次函数的关系;
4、会利用直线方程判断直线平行或垂直。
学习目标
答:(1)已知两点可以确定一条直线。
问:在平面直角坐标系内如何确定一条直线呢?
(2)已知直线上的一点和这条直线的一个方 向(斜率或倾斜角)可以确定一条直线。
斜率公式:
(x1≠x2)
研探新知
思考1:已知直线l 经过已知点P0(x0,y0),并且它的斜率是k,P(x,y)是直线l上不同于点P0的任意一点,那么x,y满足什么关系?
x
y
O
P(x,y)
l
P0(x0,y0)
关于x,y
的方程
研探新知
思考2: 那么直线l上每一点的坐标都满足
这个方程吗
由推导过程知满足
P0(x0,y0)
满足方程
研探新知
思考3:满足方程y-y0=k(x-x0)的所有点P(x,y)是否都在直线l上 为什么?
研探新知
由直线上一定点和直线的斜率确定的直线方程,叫直线的点斜式方程。
直线的点斜式方程
成立的条件:直线的斜率存在。
x
y
O
l
研探新知
思考4:当直线l 的倾斜角是0°时,直线l 的方程是什么?
x
O
y
思考5:已知直线l 经过已知点P0(x0,y0),且它的斜率不存在,直线l的方程是什么?
x
y
O
研探新知
思考6:x轴、y轴所在直线的方程分别是什么?
y=0
x=0
x
O
y
研探新知
例1 直线l 经过点P0(-2,3),且倾斜角α=45°,求直线l 的点斜式方程,并画出直线l。
解:这条直线经过点P0(-2,3),
斜率k=tan45°=1
代入点斜式方程得
y-3=x+2
O
x
y
P0
5
-5
l
例题详解
思考7:已知直线l 的斜率是k,与y轴的交点是P(0,b),求直线方程。
代入点斜式方程得,
即y= kx+b
O
x
y
直线l 的方程:y-b=k(x-0),
P(0,b)
点斜式的特例
研探新知
上述方程是由直线的斜率k与它在y轴上的截距b确定,所以方程叫做直线的斜截式方程,简称斜截式。
y=kx+b
斜截式方程:
成立的条件:直线的斜率和在y轴上的截距存在。
O
x
y
b
斜率
在y轴上的截距
我们把直线l 与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距,
研探新知
思考8:方程y=kx+b与我们学过的一次函数表达式类似,我们知道一次函数的图像是一条直线,你如何从直线方程的角度认识一次函数y=kx+b?一次函数k和b的几何意义是什么?你能说出一次函数y=2x-1,y=3x,y=-x+3的图象的特点吗?
y=2x-1的斜率为2,在y轴上的截距为-1;
y=3x的斜率为3,在y轴上的截距为0;
y=-x+3的斜率为-1,在y轴上的截距为3。
研探新知
思考9:若直线l 的斜率为k,在x轴上的截距为a,则直线l 的方程是什么?
y=k(x-a)
思考10:如何求直线y-y0=k(x-x0)在x轴、y轴上的截距?
令y=0, 可求出直线在x轴上的截距;
令x=0,可求出直线在y轴上的截距.
研探新知
x
y
O
解:
例2
例题详解
课堂训练
2.填空题:
(1)已知直线的点斜式式方程是y-2=x-1,那么此直线的斜率是 ,倾斜角是 ;
(2)已知直线的点斜式方程是y+2= (x+1),那么此直线的斜率是 ,倾斜角是 。
3.写出下列直线的斜截式方程:
课堂训练
2.斜截式方程 是点斜式的一种特
殊情况
1.直线的点斜式方程
在直线斜率存在时才能应用
在直线斜率存在,及在y轴上截距存在时才能应用,理解k,b的几何意义
3.根据方程判断平行或垂直。
课堂小结
再见
