数学人教A版(2019)选择性必修第三册8.3列联表与独立性检验(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.3列联表与独立性检验(共33张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 23:35:06 | ||
图片预览








文档简介
(共33张PPT)
2023
列联表与
独立性检验
分类变量
例如,就读不同学校是否对学生的成绩有影响,不同班级学生用于体育锻炼的时间是否有差别,吸烟是否会增加患肺癌的危险。
在现实生活里,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题。
前面我们学习的变量,如人的身高、树的高度等等,都是数值变量,数值变量的取值都为实数,其大小和运算都有实际含义。
在讨论上述问题时,为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称之为分类变量。
分类变量
分类变量的取值可以用实数表示,例如,学生所在的班级可以用1,2,3等表示,可以用数字1表示男性,数字0表示女性。
如果X表示受访者的性别,并且记X=0表示男性,X=1表示女性
如果Y表示受访者是否抽烟,并且记Y=0表示抽烟,Y=1表示不抽烟
比如我们研究一个问题:吸烟是否与性别有关。
那么,我们的变量其实有两类,是否吸烟以及性别
那么,请同学们思考一下,
这个条件概率表示的是什么?
受访者不抽烟的概率下,受访者是男性的概率
分类变量
这些数值可以只作为编号使用,并没有通常的大小和运算意义,本节我们主要讨论取值于{0,1}的分类变量的关联性问题。
如果X表示受访者的性别,并且记X=0表示男性,X=1表示女性
如果Y表示受访者是否抽烟,并且记Y=0表示抽烟,Y=1表示不抽烟
情境引入
为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响。为此对学生是否经常锻炼的情况进行了普查,全校学生的普查数据如下:
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
情景引入
最常见的方法是:我们比较经常锻炼的学生在女生和男生中的比率。
情景引入
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
该校的女生和男生在体育锻炼的经常性方面有差异
男生经常锻炼的比率比女生高出15.4个百分点,所以男生更经常锻炼
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
方法探究(二)
我们从分类变量的角度来思考这个问题
性别对体育锻炼的经常性没有影响
性别对体育锻炼的经常性有影响
列表
性别 锻炼 合计
不经常(Y=0) 经常(Y=1) 女生(X=0)
男生(X=1)
合计
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
该校的女生和男生在体育锻炼的经常性方面有差异,男生更经常锻炼
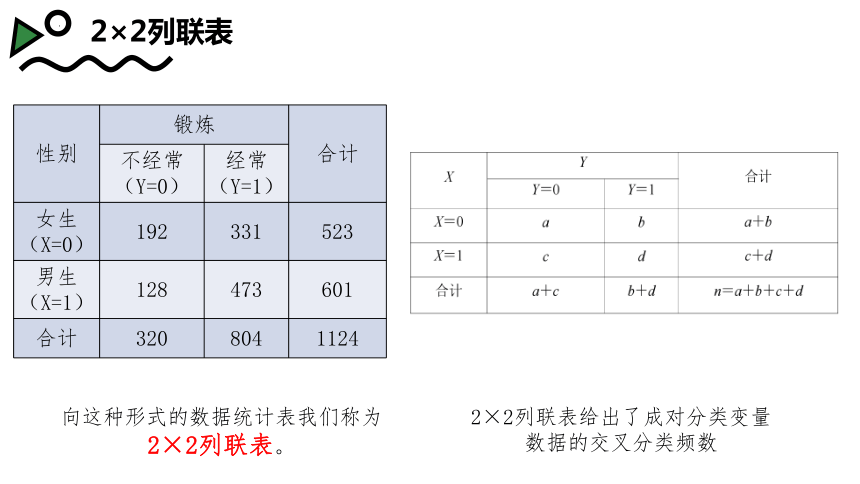
2×2列联表
性别 锻炼 合计
不经常(Y=0) 经常(Y=1) 女生(X=0) 192 331 523
男生(X=1) 128 473 601
合计 320 804 1124
向这种形式的数据统计表我们称为2×2列联表。
2×2列联表给出了成对分类变量数据的交叉分类频数
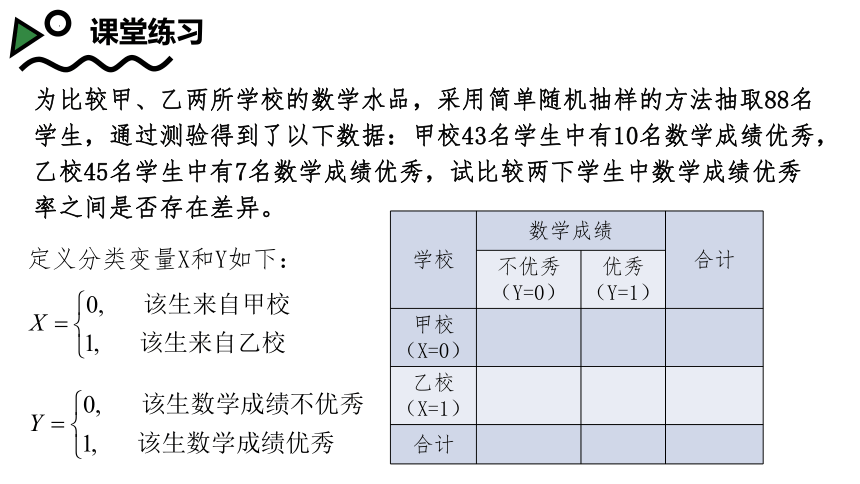
课堂练习
为比较甲、乙两所学校的数学水品,采用简单随机抽样的方法抽取88名学生,通过测验得到了以下数据:甲校43名学生中有10名数学成绩优秀,乙校45名学生中有7名数学成绩优秀,试比较两下学生中数学成绩优秀率之间是否存在差异。
定义分类变量X和Y如下:
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0)
乙校(X=1)
合计
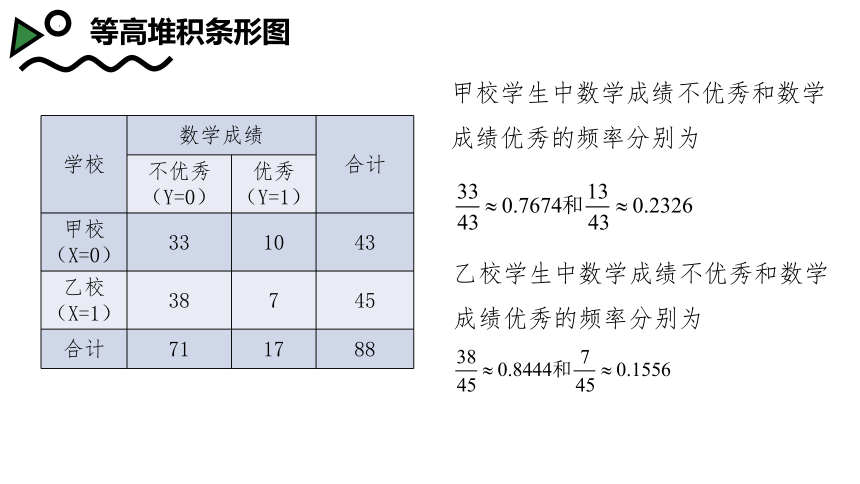
等高堆积条形图
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
等高堆积条形图
甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
等高堆积条形图
观察相同颜色区域的高度,如果两个高度相差比较明显,就判断两个分类变量之间有关系
高考调研
高考调研
高考调研
高考调研
高考调研
高考调研
独立性检验
零假设或原假设
独立性检验
独立性检验
检验两件事是否互相影响或者是否有关联,只需要检验他们对应的分类变量是否独立即可
独立性检验
这个临界值就是判断卡方大小的标准
独立性检验
高考调研
高考调研
高考调研
χ2≥xα
高考调研
高考调研
高考调研
高考调研
高考调研
2023
列联表与
独立性检验
分类变量
例如,就读不同学校是否对学生的成绩有影响,不同班级学生用于体育锻炼的时间是否有差别,吸烟是否会增加患肺癌的危险。
在现实生活里,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题。
前面我们学习的变量,如人的身高、树的高度等等,都是数值变量,数值变量的取值都为实数,其大小和运算都有实际含义。
在讨论上述问题时,为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称之为分类变量。
分类变量
分类变量的取值可以用实数表示,例如,学生所在的班级可以用1,2,3等表示,可以用数字1表示男性,数字0表示女性。
如果X表示受访者的性别,并且记X=0表示男性,X=1表示女性
如果Y表示受访者是否抽烟,并且记Y=0表示抽烟,Y=1表示不抽烟
比如我们研究一个问题:吸烟是否与性别有关。
那么,我们的变量其实有两类,是否吸烟以及性别
那么,请同学们思考一下,
这个条件概率表示的是什么?
受访者不抽烟的概率下,受访者是男性的概率
分类变量
这些数值可以只作为编号使用,并没有通常的大小和运算意义,本节我们主要讨论取值于{0,1}的分类变量的关联性问题。
如果X表示受访者的性别,并且记X=0表示男性,X=1表示女性
如果Y表示受访者是否抽烟,并且记Y=0表示抽烟,Y=1表示不抽烟
情境引入
为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响。为此对学生是否经常锻炼的情况进行了普查,全校学生的普查数据如下:
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
情景引入
最常见的方法是:我们比较经常锻炼的学生在女生和男生中的比率。
情景引入
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
该校的女生和男生在体育锻炼的经常性方面有差异
男生经常锻炼的比率比女生高出15.4个百分点,所以男生更经常锻炼
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
方法探究(二)
我们从分类变量的角度来思考这个问题
性别对体育锻炼的经常性没有影响
性别对体育锻炼的经常性有影响
列表
性别 锻炼 合计
不经常(Y=0) 经常(Y=1) 女生(X=0)
男生(X=1)
合计
523名女生中有331名经常锻炼,601名男生中有473名经常锻炼。
该校的女生和男生在体育锻炼的经常性方面有差异,男生更经常锻炼
2×2列联表
性别 锻炼 合计
不经常(Y=0) 经常(Y=1) 女生(X=0) 192 331 523
男生(X=1) 128 473 601
合计 320 804 1124
向这种形式的数据统计表我们称为2×2列联表。
2×2列联表给出了成对分类变量数据的交叉分类频数
课堂练习
为比较甲、乙两所学校的数学水品,采用简单随机抽样的方法抽取88名学生,通过测验得到了以下数据:甲校43名学生中有10名数学成绩优秀,乙校45名学生中有7名数学成绩优秀,试比较两下学生中数学成绩优秀率之间是否存在差异。
定义分类变量X和Y如下:
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0)
乙校(X=1)
合计
等高堆积条形图
学校 数学成绩 合计
不优秀(Y=0) 优秀(Y=1) 甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
等高堆积条形图
甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为
等高堆积条形图
观察相同颜色区域的高度,如果两个高度相差比较明显,就判断两个分类变量之间有关系
高考调研
高考调研
高考调研
高考调研
高考调研
高考调研
独立性检验
零假设或原假设
独立性检验
独立性检验
检验两件事是否互相影响或者是否有关联,只需要检验他们对应的分类变量是否独立即可
独立性检验
这个临界值就是判断卡方大小的标准
独立性检验
高考调研
高考调研
高考调研
χ2≥xα
高考调研
高考调研
高考调研
高考调研
高考调研
