数学人教A版(2019)选择性必修第三册7.2离散型随机变量及其分布列(共47张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.2离散型随机变量及其分布列(共47张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 59.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-04 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
7.2 离散型随机变量及其分布列
第七章 随机变量及其分布
学习目标
0 1
0 2
理解离散型随机变量的含义,会用离散型随机变量描述随机现象.(重点)
掌握离散型随机变量分布列的表示方法及性质,了解两点分布.(难点)
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题.类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
随机试验的样本点与实数的关系
探究
考察下列随机试验及其引入的变量:
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
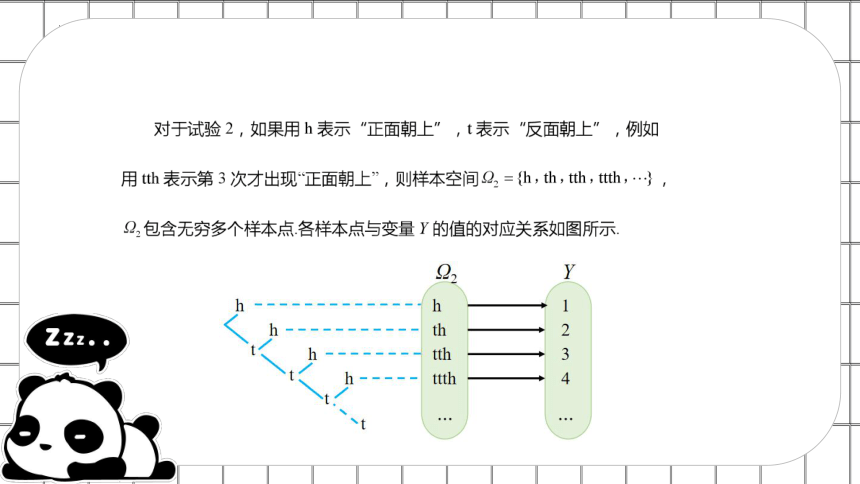
试验2:抛掷一枚硬币直到出现正面为止,变量Y表示需要的抛掷次数.
这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?变量X,Y有哪些共同的特征?
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应. 变量 X,Y 有如下共同点:
(1)取值依赖于样本点;
(2)所有可能取值是明确的.
随机变量与离散型随机变量
随机变量与函数的异同点
现实生活中,离散型随机变量的例子有很多.例如,某射击运动员射击一次可能命中的环数X,它的可能取值为0,1,2,…,10;某网页在24h内被浏览的次数Y,它的可能取值为0,1,2,…;等等.
现实生活中还有大量不是离散型随机变量的例子.例如,种子含水量的测量误差X1;某品牌电视机的使用寿命X2;测量某一个零件的长度产生的测量误差X3.这些都是可能取值充满了某个区间、不能一一列举的随机变量.本节我们只研究取有限个值的离散型随机变量.
连续型随机变量
根据问题引入合适的随机变量,有利于我们简洁地表示所关心的随机事件,并利用数学工具研究随机试验中的概率问题.
例如,掷一枚质地均匀的骰子,X表示掷出的点数,则事件“掷出m点”可以表示为{X=m} (m=1, 2, 3, 4, 5, 6),
事件“掷出的点数不大于2”可以表示为 ,
事件“掷出偶数点”可以表示为{X=2}∪{X=4}∪{X=6},等等.
由掷出各种点数的等可能性,我们还可以得到
这一规律我们还可以用下表来表示.
离散型随机变量的概率分布列
与函数的表示法类似,离散型随机变量的分布列也可以用表格表示,还可以用图形表示. 例如,下图直观地表示了掷骰子试验中掷出的点数X的分布列,称为X的概率分布图.
分布列的性质
利用分布列和概率的性质,可以计算由离散型随机变量表示的事件的概率. 例如,在掷骰子试验中,由概率的加法公式,得事件“掷出的点数不大于2”的概率为
类似地,事件“掷出偶数点”的概率为
我们称X服从两点分布或0-1分布. 实际上,X为在一次试验中成功(事件A发生)的次数(0或1).
像购买的彩券是否中奖,新生婴儿的性别,投篮是否命中等,都可以用两点分布来描述.
两点分布
例题巩固
利用分布列及其性质解题时的两点注意
方法总结1
例3 一批笔记本电脑共有 10 台,其中 A 品牌 3 台,B 品牌 7 台.如果从中随机挑选 2 台,求这 2 台电脑中 A 品牌台数的分布列.
方法总结2
求离散型随机变量的分布列,首先要根据具体情况确定ξ的取值情况,然后利用排列、组合与概率知识求出ξ取各个值的概率,即必须解决好两个问题,一是求出ξ的所有取值,二是求出ξ取每一个值时的概率.
练习提升
A
D
C
C
A
0.2
课堂小结:
1.离散型随机变量的概念.
2.离散型随机变量的分布列的概念及其性质.
3.两点分布.
感 谢 观看!
7.2 离散型随机变量及其分布列
第七章 随机变量及其分布
学习目标
0 1
0 2
理解离散型随机变量的含义,会用离散型随机变量描述随机现象.(重点)
掌握离散型随机变量分布列的表示方法及性质,了解两点分布.(难点)
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题.类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
随机试验的样本点与实数的关系
探究
考察下列随机试验及其引入的变量:
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y表示需要的抛掷次数.
这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?变量X,Y有哪些共同的特征?
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应. 变量 X,Y 有如下共同点:
(1)取值依赖于样本点;
(2)所有可能取值是明确的.
随机变量与离散型随机变量
随机变量与函数的异同点
现实生活中,离散型随机变量的例子有很多.例如,某射击运动员射击一次可能命中的环数X,它的可能取值为0,1,2,…,10;某网页在24h内被浏览的次数Y,它的可能取值为0,1,2,…;等等.
现实生活中还有大量不是离散型随机变量的例子.例如,种子含水量的测量误差X1;某品牌电视机的使用寿命X2;测量某一个零件的长度产生的测量误差X3.这些都是可能取值充满了某个区间、不能一一列举的随机变量.本节我们只研究取有限个值的离散型随机变量.
连续型随机变量
根据问题引入合适的随机变量,有利于我们简洁地表示所关心的随机事件,并利用数学工具研究随机试验中的概率问题.
例如,掷一枚质地均匀的骰子,X表示掷出的点数,则事件“掷出m点”可以表示为{X=m} (m=1, 2, 3, 4, 5, 6),
事件“掷出的点数不大于2”可以表示为 ,
事件“掷出偶数点”可以表示为{X=2}∪{X=4}∪{X=6},等等.
由掷出各种点数的等可能性,我们还可以得到
这一规律我们还可以用下表来表示.
离散型随机变量的概率分布列
与函数的表示法类似,离散型随机变量的分布列也可以用表格表示,还可以用图形表示. 例如,下图直观地表示了掷骰子试验中掷出的点数X的分布列,称为X的概率分布图.
分布列的性质
利用分布列和概率的性质,可以计算由离散型随机变量表示的事件的概率. 例如,在掷骰子试验中,由概率的加法公式,得事件“掷出的点数不大于2”的概率为
类似地,事件“掷出偶数点”的概率为
我们称X服从两点分布或0-1分布. 实际上,X为在一次试验中成功(事件A发生)的次数(0或1).
像购买的彩券是否中奖,新生婴儿的性别,投篮是否命中等,都可以用两点分布来描述.
两点分布
例题巩固
利用分布列及其性质解题时的两点注意
方法总结1
例3 一批笔记本电脑共有 10 台,其中 A 品牌 3 台,B 品牌 7 台.如果从中随机挑选 2 台,求这 2 台电脑中 A 品牌台数的分布列.
方法总结2
求离散型随机变量的分布列,首先要根据具体情况确定ξ的取值情况,然后利用排列、组合与概率知识求出ξ取各个值的概率,即必须解决好两个问题,一是求出ξ的所有取值,二是求出ξ取每一个值时的概率.
练习提升
A
D
C
C
A
0.2
课堂小结:
1.离散型随机变量的概念.
2.离散型随机变量的分布列的概念及其性质.
3.两点分布.
感 谢 观看!
