7.1.2 垂线同步练习题(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
1 两条直线的位置关系
2 垂线
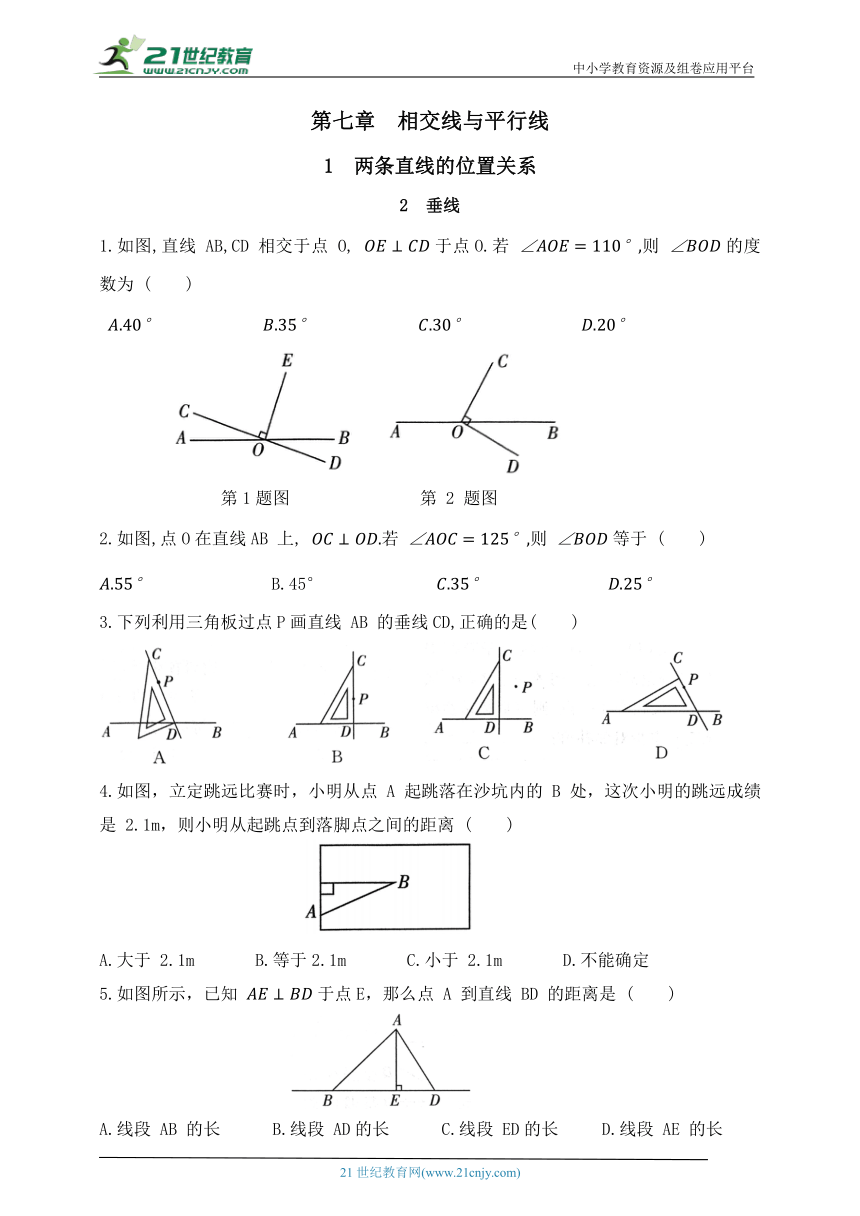
1.如图,直线 AB,CD 相交于点 O, 于点O.若 则 的度数为 ( )
第1题图 第 2 题图
2.如图,点O在直线AB 上, 若 则 等于 ( )
B.45°
3.下列利用三角板过点P画直线 AB 的垂线CD,正确的是( )
4.如图,立定跳远比赛时,小明从点 A 起跳落在沙坑内的 B 处,这次小明的跳远成绩是 2.1m,则小明从起跳点到落脚点之间的距离 ( )
A.大于 2.1m B.等于2.1m C.小于 2.1m D.不能确定
5.如图所示,已知 于点E,那么点 A 到直线 BD 的距离是 ( )
A.线段 AB 的长 B.线段 AD的长 C.线段 ED的长 D.线段 AE 的长
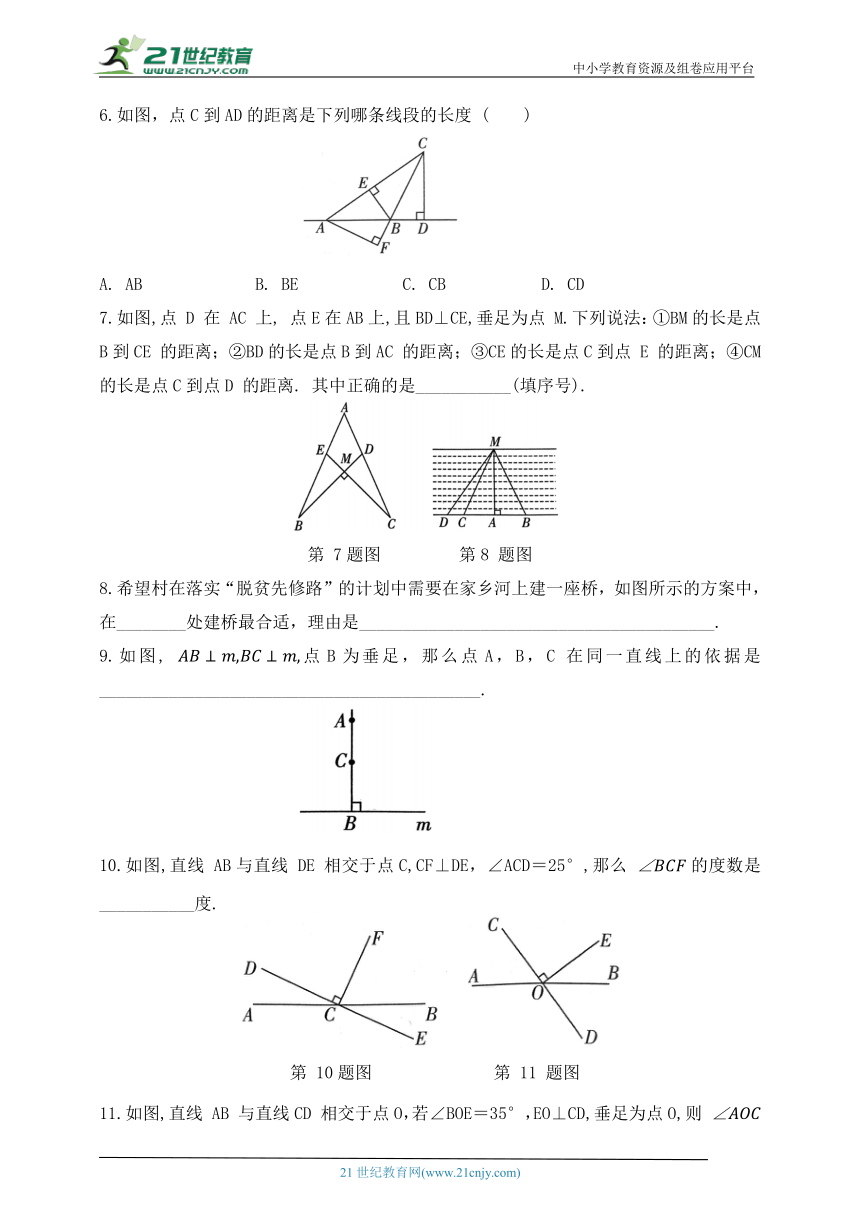
6.如图,点C到AD的距离是下列哪条线段的长度 ( )
A. AB B. BE C. CB D. CD
7.如图,点 D 在 AC 上, 点E在AB上,且BD⊥CE,垂足为点 M.下列说法:①BM的长是点 B到CE 的距离;②BD的长是点B到AC 的距离;③CE的长是点C到点 E 的距离;④CM 的长是点C到点D 的距离. 其中正确的是___________(填序号).
第 7题图 第8 题图
8.希望村在落实“脱贫先修路”的计划中需要在家乡河上建一座桥,如图所示的方案中,在________处建桥最合适,理由是_________________________________________.
9.如图, 点B为垂足,那么点A,B,C 在同一直线上的依据是____________________________________________.
10.如图,直线 AB与直线 DE 相交于点C,CF⊥DE,∠ACD=25°,那么 的度数是___________度.
第 10题图 第 11 题图
11.如图,直线 AB 与直线CD 相交于点O,若∠BOE=35°,EO⊥CD,垂足为点O,则 =_____________°.
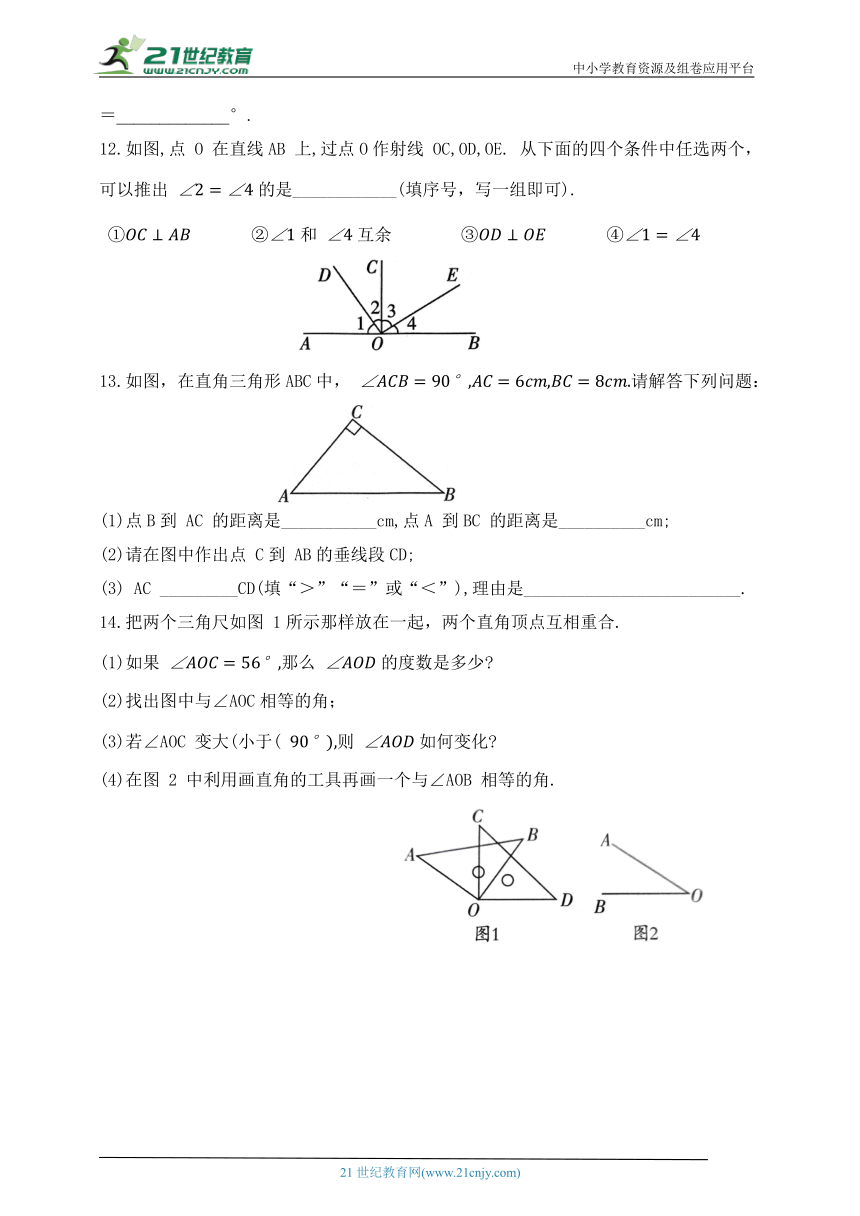
12.如图,点 O 在直线AB 上,过点O作射线 OC,OD,OE. 从下面的四个条件中任选两个,可以推出 的是____________(填序号,写一组即可).
②和 互余
13.如图,在直角三角形ABC中, 请解答下列问题:
(1)点B到 AC 的距离是___________cm,点A 到BC 的距离是__________cm;
(2)请在图中作出点 C到 AB的垂线段CD;
(3) AC _________CD(填“>”“=”或“<”),理由是_________________________.
14.把两个三角尺如图 1所示那样放在一起,两个直角顶点互相重合.
(1)如果 那么 的度数是多少
(2)找出图中与∠AOC相等的角;
(3)若∠AOC 变大(小于( 则 如何变化
(4)在图 2 中利用画直角的工具再画一个与∠AOB 相等的角.
15.如图,直线 AB,CD 相交于点O,OM⊥CD于点O,
(1)求∠AOM的度数;
(2)若OA 平分∠MOE,求∠BOE的度数.
16.如图,直线 AB,CD 相交于点O,
(1)若 试判断 ON 与CD的位置关系,并说明理由;
(2)若 求 的度数.
17.如图,直线 AB,CD 相交于点O, OE 平分
(1)若 求 的度数;
(2)若 请直接写出 的度数(用含α的式子表示).
参考答案
1. D 2. C 3. B 4. A 5. D 6. D
7.①③ 8. MA 垂线段最短
9.平面内,过一点有且只有一条直线与已知直线垂直
10.65 11.55
12.①③(答案不唯一)
13.解:(1)8,6;
(2)如图,CD即为所求作;
(3)>,垂线段最短.
14.解:(1)因为, 所以
理由如下:
因为 所以
所以 所以图中与∠AOC相等的角是∠BOD;
(3)变大.理由如下:
因为∠DOC=90°,所以∠AOD=∠AOC+∠DOC=∠AOC+90°,
所以当∠AOC 变大时,则∠AOD变大;
(4)如图所示,∠COD即为所求作;
用三角板 和直尺过点 O 分别作OC⊥OB,OD⊥OA,
所以∠BOC=∠AOD=90°,所以∠AOB+∠AOC=∠COD+∠AOC,
所以∠COD=∠AOB.
15.解:(1)因为 OM⊥CD,所以∠MOC=90°,
因为∠AOC=∠BOD=28°,所以∠AOM=∠MOC-∠AOC=90°-28°=62°;
(2)因为 OA 平分∠MOE,所以∠AOE=∠AOM=62°,
因为∠BOE+∠AOE=180°,所以∠BOE=180°-∠AOE=180°-62°=118°.
16.解:(1)ON 与CD 互相垂直.
理由如下:
因为 OM⊥AB,所以∠MOA=∠BOM=90°,所以∠1+∠AOC=90°,
又因为∠1=∠2,所以∠2+∠AOC=90°,即∠NOC=90°,
所以 ON⊥CD;
(2) 因 为∠BOC= 4∠1,∠BOC =∠1 +∠BOM=∠1+90°,
所以∠1+90°=4∠1,所以∠1=30°,
所以∠MOD=180°-∠1=150°.
17.解:(1)因为 OE 平分∠BOD,所以
因为 AB⊥OF,所以∠BOF=90°,
所以∠EOF=∠BOE+∠BOF=90°+35°=125°;
(2)因为∠EOF=α,AB⊥OF,所以∠BOE=α-90°,
因为OE平分∠BOD.所以∠BOD=2∠BOE=2(α-90°)=2α-180°.
所以∠AOC=∠BOD=2α-180°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
1 两条直线的位置关系
2 垂线
1.如图,直线 AB,CD 相交于点 O, 于点O.若 则 的度数为 ( )
第1题图 第 2 题图
2.如图,点O在直线AB 上, 若 则 等于 ( )
B.45°
3.下列利用三角板过点P画直线 AB 的垂线CD,正确的是( )
4.如图,立定跳远比赛时,小明从点 A 起跳落在沙坑内的 B 处,这次小明的跳远成绩是 2.1m,则小明从起跳点到落脚点之间的距离 ( )
A.大于 2.1m B.等于2.1m C.小于 2.1m D.不能确定
5.如图所示,已知 于点E,那么点 A 到直线 BD 的距离是 ( )
A.线段 AB 的长 B.线段 AD的长 C.线段 ED的长 D.线段 AE 的长
6.如图,点C到AD的距离是下列哪条线段的长度 ( )
A. AB B. BE C. CB D. CD
7.如图,点 D 在 AC 上, 点E在AB上,且BD⊥CE,垂足为点 M.下列说法:①BM的长是点 B到CE 的距离;②BD的长是点B到AC 的距离;③CE的长是点C到点 E 的距离;④CM 的长是点C到点D 的距离. 其中正确的是___________(填序号).
第 7题图 第8 题图
8.希望村在落实“脱贫先修路”的计划中需要在家乡河上建一座桥,如图所示的方案中,在________处建桥最合适,理由是_________________________________________.
9.如图, 点B为垂足,那么点A,B,C 在同一直线上的依据是____________________________________________.
10.如图,直线 AB与直线 DE 相交于点C,CF⊥DE,∠ACD=25°,那么 的度数是___________度.
第 10题图 第 11 题图
11.如图,直线 AB 与直线CD 相交于点O,若∠BOE=35°,EO⊥CD,垂足为点O,则 =_____________°.
12.如图,点 O 在直线AB 上,过点O作射线 OC,OD,OE. 从下面的四个条件中任选两个,可以推出 的是____________(填序号,写一组即可).
②和 互余
13.如图,在直角三角形ABC中, 请解答下列问题:
(1)点B到 AC 的距离是___________cm,点A 到BC 的距离是__________cm;
(2)请在图中作出点 C到 AB的垂线段CD;
(3) AC _________CD(填“>”“=”或“<”),理由是_________________________.
14.把两个三角尺如图 1所示那样放在一起,两个直角顶点互相重合.
(1)如果 那么 的度数是多少
(2)找出图中与∠AOC相等的角;
(3)若∠AOC 变大(小于( 则 如何变化
(4)在图 2 中利用画直角的工具再画一个与∠AOB 相等的角.
15.如图,直线 AB,CD 相交于点O,OM⊥CD于点O,
(1)求∠AOM的度数;
(2)若OA 平分∠MOE,求∠BOE的度数.
16.如图,直线 AB,CD 相交于点O,
(1)若 试判断 ON 与CD的位置关系,并说明理由;
(2)若 求 的度数.
17.如图,直线 AB,CD 相交于点O, OE 平分
(1)若 求 的度数;
(2)若 请直接写出 的度数(用含α的式子表示).
参考答案
1. D 2. C 3. B 4. A 5. D 6. D
7.①③ 8. MA 垂线段最短
9.平面内,过一点有且只有一条直线与已知直线垂直
10.65 11.55
12.①③(答案不唯一)
13.解:(1)8,6;
(2)如图,CD即为所求作;
(3)>,垂线段最短.
14.解:(1)因为, 所以
理由如下:
因为 所以
所以 所以图中与∠AOC相等的角是∠BOD;
(3)变大.理由如下:
因为∠DOC=90°,所以∠AOD=∠AOC+∠DOC=∠AOC+90°,
所以当∠AOC 变大时,则∠AOD变大;
(4)如图所示,∠COD即为所求作;
用三角板 和直尺过点 O 分别作OC⊥OB,OD⊥OA,
所以∠BOC=∠AOD=90°,所以∠AOB+∠AOC=∠COD+∠AOC,
所以∠COD=∠AOB.
15.解:(1)因为 OM⊥CD,所以∠MOC=90°,
因为∠AOC=∠BOD=28°,所以∠AOM=∠MOC-∠AOC=90°-28°=62°;
(2)因为 OA 平分∠MOE,所以∠AOE=∠AOM=62°,
因为∠BOE+∠AOE=180°,所以∠BOE=180°-∠AOE=180°-62°=118°.
16.解:(1)ON 与CD 互相垂直.
理由如下:
因为 OM⊥AB,所以∠MOA=∠BOM=90°,所以∠1+∠AOC=90°,
又因为∠1=∠2,所以∠2+∠AOC=90°,即∠NOC=90°,
所以 ON⊥CD;
(2) 因 为∠BOC= 4∠1,∠BOC =∠1 +∠BOM=∠1+90°,
所以∠1+90°=4∠1,所以∠1=30°,
所以∠MOD=180°-∠1=150°.
17.解:(1)因为 OE 平分∠BOD,所以
因为 AB⊥OF,所以∠BOF=90°,
所以∠EOF=∠BOE+∠BOF=90°+35°=125°;
(2)因为∠EOF=α,AB⊥OF,所以∠BOE=α-90°,
因为OE平分∠BOD.所以∠BOD=2∠BOE=2(α-90°)=2α-180°.
所以∠AOC=∠BOD=2α-180°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
