2024年九年级数学中考总复习: 关于角分线的方法技巧 讲义(无答案)
文档属性
| 名称 | 2024年九年级数学中考总复习: 关于角分线的方法技巧 讲义(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 325.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-06 08:39:26 | ||
图片预览

文档简介
关于角平分线的方法技巧
类型 1 构造双垂直(核心:构造翻折全等)
遇到角平分线上一点到角的一边的垂线的问题,
过该点作另一边的垂线,构造双垂直:
解题思路:运用角的平分线上的点到角的两边的距离相等(PA=PB)求解。
例1.如图,在四边形ABCD中,CA平分过点A作垂足为 E,猜想线段 AC与AE之间的数量关系,并证明你的结论.
练习题
【问题情境】数学活动课上,李老师出示了一个问题:如图1,在中,AD平分 CD,求证:
同学们纷纷表达了自己的想法:
小琦:题中给出的条件不能直接证明两个三角形全等;
小锦:已知AD平分,根据角平分线上的点到角的两边的距离相等,分别作点D到AB,AC的垂线,可以得到线段相等,从而证明三角形全等.
【独立思考】(1)请根据两位同学的思路解答李老师提出的问题;
【实践探究】(2)在原有问题条件不变的情况下,李老师增加下面的条件,并提出新问题,请你解答:如图2,过点C作直线作DE交直线l于点E,则AD与ED之间的数量关系为 ;
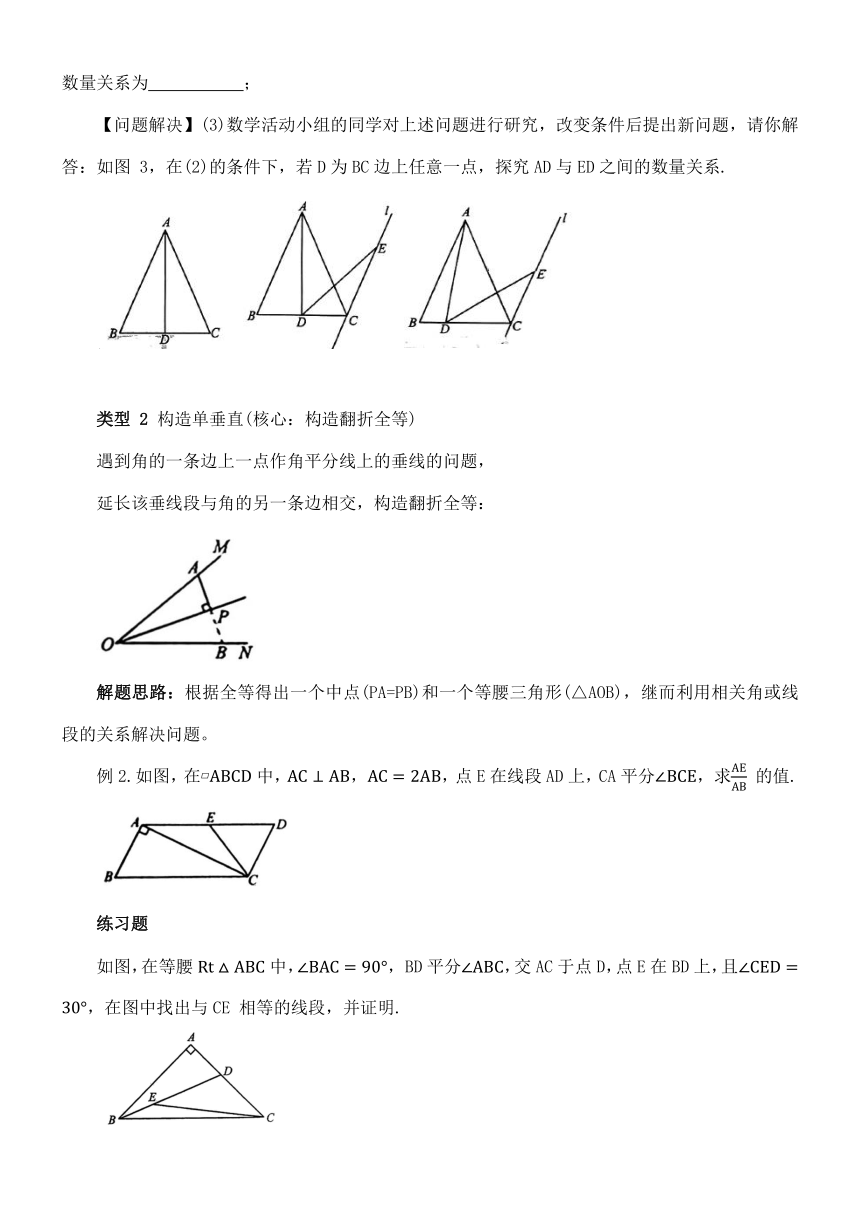
【问题解决】(3)数学活动小组的同学对上述问题进行研究,改变条件后提出新问题,请你解答:如图 3,在(2)的条件下,若D为BC边上任意一点,探究AD与ED之间的数量关系.
类型 2 构造单垂直(核心:构造翻折全等)
遇到角的一条边上一点作角平分线上的垂线的问题,
延长该垂线段与角的另一条边相交,构造翻折全等:
解题思路:根据全等得出一个中点(PA=PB)和一个等腰三角形(△AOB),继而利用相关角或线段的关系解决问题。
例2.如图,在中,,点E在线段AD上,CA平分求 的值.
练习题
如图,在等腰中,BD平分,交AC于点D,点E在BD上,且,在图中找出与CE 相等的线段,并证明.
类型 3 构造等长线段(核心:构造翻折全等)
遇到角平分线上一点与角的一边上的点连接线段的问题,
在角的另一边上截取等长线段,构造翻折全等:
解题思路:根据全等得出相关角或线段的关系。
例3.如图,在中,BD平分交AC于点D,延长BD至点E,使连接CE,求证:
练习题
如图,在中,AD为的平分线,点E在边AC上,,AD,BE相交于F,交BC于点G .
(1)求证:
(2)在图中找一条与CD相等的线段,并证明你的结论.
类型 4 构造平行线
遇到角平分线上一点的问题,
过该点作角的一边的平行线:
解题思路:作平行线得到等腰三角形(△POQ), 筒记:“平分+平行=等腰”。
例4.如图,在等腰中,AD平分交BC于点D,点E在AC的延长线上,且 若,求CD的长.
练习题
如图,在中,BD平分交AC于点D,过点C作交BD的延长线于点E,若,求EC的长.
类型 1 构造双垂直(核心:构造翻折全等)
遇到角平分线上一点到角的一边的垂线的问题,
过该点作另一边的垂线,构造双垂直:
解题思路:运用角的平分线上的点到角的两边的距离相等(PA=PB)求解。
例1.如图,在四边形ABCD中,CA平分过点A作垂足为 E,猜想线段 AC与AE之间的数量关系,并证明你的结论.
练习题
【问题情境】数学活动课上,李老师出示了一个问题:如图1,在中,AD平分 CD,求证:
同学们纷纷表达了自己的想法:
小琦:题中给出的条件不能直接证明两个三角形全等;
小锦:已知AD平分,根据角平分线上的点到角的两边的距离相等,分别作点D到AB,AC的垂线,可以得到线段相等,从而证明三角形全等.
【独立思考】(1)请根据两位同学的思路解答李老师提出的问题;
【实践探究】(2)在原有问题条件不变的情况下,李老师增加下面的条件,并提出新问题,请你解答:如图2,过点C作直线作DE交直线l于点E,则AD与ED之间的数量关系为 ;
【问题解决】(3)数学活动小组的同学对上述问题进行研究,改变条件后提出新问题,请你解答:如图 3,在(2)的条件下,若D为BC边上任意一点,探究AD与ED之间的数量关系.
类型 2 构造单垂直(核心:构造翻折全等)
遇到角的一条边上一点作角平分线上的垂线的问题,
延长该垂线段与角的另一条边相交,构造翻折全等:
解题思路:根据全等得出一个中点(PA=PB)和一个等腰三角形(△AOB),继而利用相关角或线段的关系解决问题。
例2.如图,在中,,点E在线段AD上,CA平分求 的值.
练习题
如图,在等腰中,BD平分,交AC于点D,点E在BD上,且,在图中找出与CE 相等的线段,并证明.
类型 3 构造等长线段(核心:构造翻折全等)
遇到角平分线上一点与角的一边上的点连接线段的问题,
在角的另一边上截取等长线段,构造翻折全等:
解题思路:根据全等得出相关角或线段的关系。
例3.如图,在中,BD平分交AC于点D,延长BD至点E,使连接CE,求证:
练习题
如图,在中,AD为的平分线,点E在边AC上,,AD,BE相交于F,交BC于点G .
(1)求证:
(2)在图中找一条与CD相等的线段,并证明你的结论.
类型 4 构造平行线
遇到角平分线上一点的问题,
过该点作角的一边的平行线:
解题思路:作平行线得到等腰三角形(△POQ), 筒记:“平分+平行=等腰”。
例4.如图,在等腰中,AD平分交BC于点D,点E在AC的延长线上,且 若,求CD的长.
练习题
如图,在中,BD平分交AC于点D,过点C作交BD的延长线于点E,若,求EC的长.
同课章节目录
