5.3平行线的性质 同步练2023-2024学年人教版七年级数学下册(含答案)
文档属性
| 名称 | 5.3平行线的性质 同步练2023-2024学年人教版七年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 479.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-05 22:32:46 | ||
图片预览



文档简介
5.3. 平行线的性质 同步练
一.选择题(共12小题)
1.下列说法中,正确的是( )
A.经过直线外一点,有且只有一条直线与这条直线平行
B.同旁内角相等,两直线平行
C.相等的角是对顶角
D.若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补
2.凸透镜是中央较厚边缘较薄的透镜.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线交于点P,点F为焦点,若∠1=30°,∠2=55°,则∠ABP的度数是( )
A.150° B.155° C.160° D.165°
3.下列说法正确的是( )
A.同位角相等
B.对顶角相等
C.两条直线被第三条直线所截,内错角相等
D.两条平行直线被第三条直线所截,同旁内角相等
4.如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=22°,则∠CEF等于( )
A.112° B.122° C.88° D.68°
5.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形ABC是三角板),其依据是( )
A.同旁内角互补,两直线平行
B.两直线平行,同旁内角互补
C.同位角相等,两直线平行
D.两直线平行,同位角相等
6.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.138° B.136° C.134° D.132°
7.下列选项中,可以用来说明命题“若|a|>3,则a>3”是假命题的反例是( )
A.a=﹣5 B.a=﹣3 C.a=﹣2 D.a=4
8.如图所示,图形中∠1与∠2不一定相等的是( )
A. B.
C. D.
9.如图,直线a与直线b、c都相交,若b∥c,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.140°
10.下列命题的逆命题是真命题的是( )
A.对顶角相等
B.同一三角形内等角对等边
C.同角的余角相等
D.全等三角形对应角相等
11.如图,AB∥CD,∠ABE=150°,∠BEF=70°,则∠DFE的度数为( )
A.30° B.40° C.50° D.60°
12.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:
①GH∥BC,②∠D=∠F,
③HE平分∠AHG,④DE⊥AB,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
13.如图,直线a,b被直线c所截,a∥b,∠1=42°13′,则∠2的度数为 .
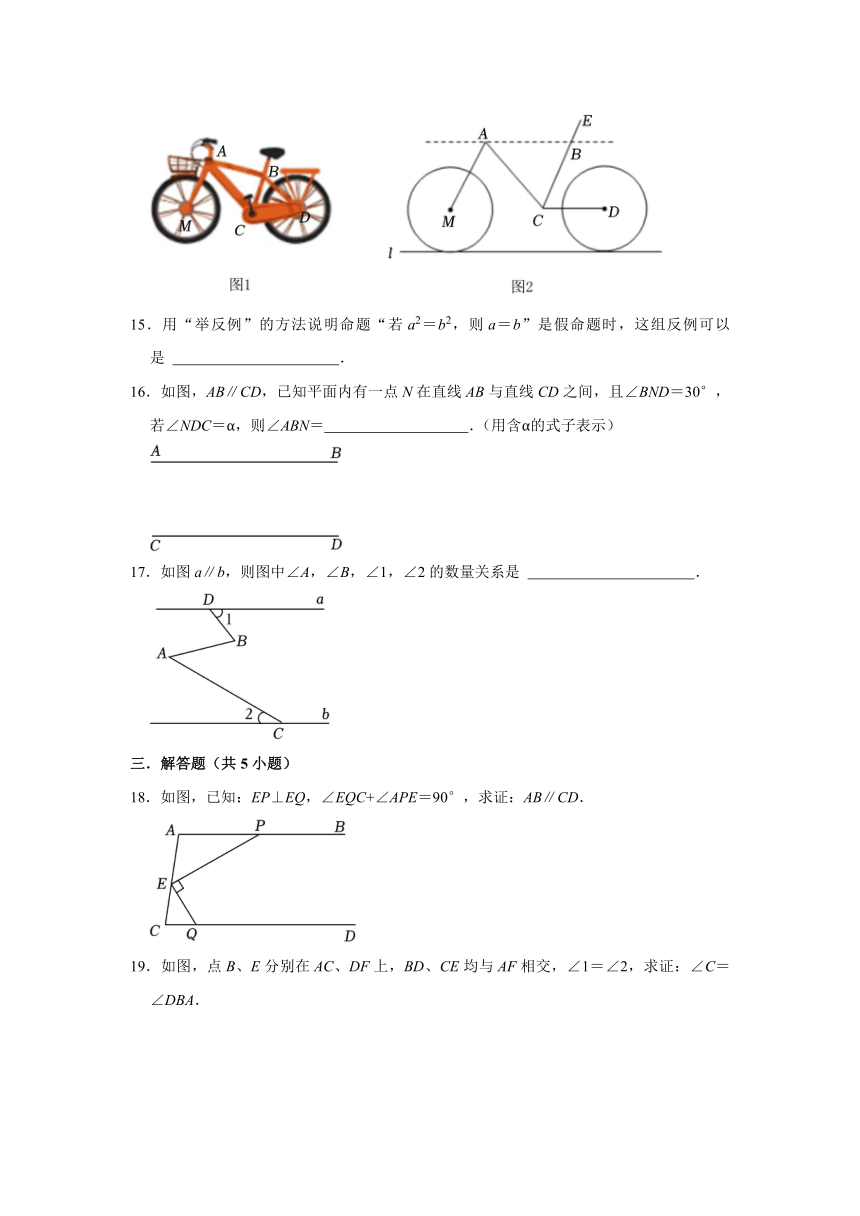
14.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图.其中AB、CD都与地面l平行,∠BCD=60°,∠BAC=54°,当∠MAC为 度时.AM与CB平行.
15.用“举反例”的方法说明命题“若a2=b2,则a=b”是假命题时,这组反例可以是 .
16.如图,AB∥CD,已知平面内有一点N在直线AB与直线CD之间,且∠BND=30°,若∠NDC=α,则∠ABN= .(用含α的式子表示)
17.如图a∥b,则图中∠A,∠B,∠1,∠2的数量关系是 .
三.解答题(共5小题)
18.如图,已知:EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD.
19.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,求证:∠C=∠DBA.
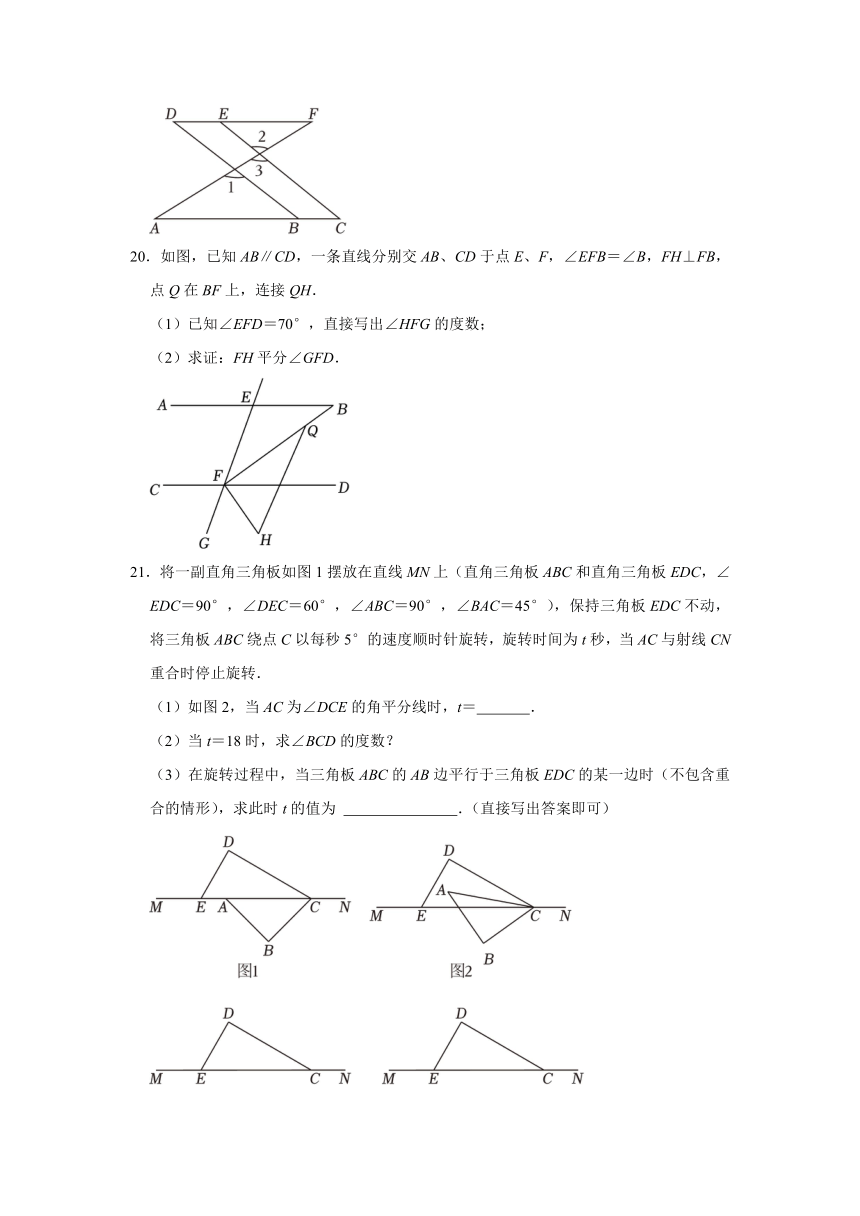
20.如图,已知AB∥CD,一条直线分别交AB、CD于点E、F,∠EFB=∠B,FH⊥FB,点Q在BF上,连接QH.
(1)已知∠EFD=70°,直接写出∠HFG的度数;
(2)求证:FH平分∠GFD.
21.将一副直角三角板如图1摆放在直线MN上(直角三角板ABC和直角三角板EDC,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°),保持三角板EDC不动,将三角板ABC绕点C以每秒5°的速度顺时针旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.
(1)如图2,当AC为∠DCE的角平分线时,t= .
(2)当t=18时,求∠BCD的度数?
(3)在旋转过程中,当三角板ABC的AB边平行于三角板EDC的某一边时(不包含重合的情形),求此时t的值为 .(直接写出答案即可)
22.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.
(1)【基础问题】如图1,试说明:∠AGD=∠A+∠D.(完成下面的填空部分)
证明:过点G作直线MN∥AB,
∵AB∥CD,
∴① ∥CD.
∵MN∥AB,
∴② =∠MGA.
∵MN∥CD,
∴∠D=③ (④ ).
∴∠AGD=∠AGM+∠AGM=∠A+∠D.
(2)【类比探究】如图2,当点G在线段EF延长线上时,请写出∠AGD、∠A、∠D三者之间的数量关系,并说明理由.
(3)【应用拓展】如图3,点E与点A重合,AH平分∠GAB,且∠HDF=22°,∠AFC=72°,那么∠H的度数为 .
参考答案
一.选择题(共12小题)
1--10ABBAC CABAB 11--12BB
二.填空题(共5小题)
13.137°47′
14.66
15.a=1,b=﹣1(答案不唯一).
16.30°﹣α或330°﹣α.
17.∠ABD﹣∠1=∠CAB﹣∠2.
三.解答题(共5小题)
18.证明:过E点作AB∥EF,
∵AB∥EF,
∴∠APE=∠PEF(两直线平行,内错角相等),
∵EP⊥EQ,
∴∠PEQ=90°(垂直的定义),
即∠QEF+∠PEF=90°,
∴∠APE+∠QEF=90°,
∵∠EQC+∠APE=90°,
∴∠EQC=∠QEF,
∴EF∥CD(内错角相等,两直线平行),
∴AB∥CD(平行于同一直线的两直线互相平行).
19.证明:∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠DBA.
20.(1)解:AB∥CD,
∴∠B=∠BFD,
∵∠EFB=∠B,
∴∠BFD=∠EFB,
∵∠EFD=70°,
∴∠EFB=∠EFD=35°,
∵FH⊥FB,
∴∠HFQ=90°,
∴∠HFG=180°﹣∠EFB﹣∠HFQ=55°;
(2)证明:由(1)知∠BFD=∠EFB,∠HFQ=90°,
∴∠HFG+∠EFB=180°﹣∠HFQ=90°,∠DFH+∠BFD=90°,
∴∠HFG=∠DFH,
∴FH平分∠GFD.
21.解:(1)当AC为∠DCE的角平分线时,旋转角为15°,
∴t==3,
故答案为3.
(2)当t=18时,旋转角为90°,如图:
∵∠DCE=30°,∠ACB=45°,
∴∠ACD=60°,∠BCD=60°﹣45°=15°.
(3)当三角板ABC的AB边平行于三角板EDC的某一边时,有3种情况:
①当AB∥DE时,如图:
此时,BC与CD重合,
t=(30+40)÷5=15,
②当AB∥CE时,如图:
∵AB∥CE,
∴∠BCE=∠B=90°,
∴∠ACE=90°+45°=135°,
∴t=135÷5=27,
③当AB∥CD时,如图:
∵AB∥CD,
∴∠BCD=∠D=90°,
∴∠ACE=30°+90°+45°=165°,
∴t=165÷3=33.
综上所述,t=15或27或33.
22.解:(1)过点G作直线MN∥AB,
又∵AB∥CD,
∴MN∥CD(平行于同一条直线的两条直线平行),
∵MN∥AB,
∴∠A=∠AGM(两直线平行,内错角相等),
∵MN∥CD,
∴∠D=∠DGM(两直线平行,内错角相等),
∴∠AGD=∠AGM+∠DGM=∠A+∠D.
故答案为:MN;∠A;∠DGM;两直线平行,内错角相等.
(2)如图所示,过点G作直线MN∥AB,
又∵AB∥CD,
∴MN∥CD,
∵MN∥AB,
∴∠A=∠AGM,
∵MN∥CD,
∴∠D=∠DGM,
∴∠AGD=∠AGM﹣∠DGM=∠A﹣∠D.
(3)如图所示,
∵∠AFC=72°;
∴∠GAB=180°﹣72°=108°,
∵AH平分∠GAB,
∴∠HAB==54°,
∵DC∥AB,
∴∠HQC=54°,
∴∠H=∠HQC﹣∠HDF=54°﹣22°=32°
一.选择题(共12小题)
1.下列说法中,正确的是( )
A.经过直线外一点,有且只有一条直线与这条直线平行
B.同旁内角相等,两直线平行
C.相等的角是对顶角
D.若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补
2.凸透镜是中央较厚边缘较薄的透镜.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线交于点P,点F为焦点,若∠1=30°,∠2=55°,则∠ABP的度数是( )
A.150° B.155° C.160° D.165°
3.下列说法正确的是( )
A.同位角相等
B.对顶角相等
C.两条直线被第三条直线所截,内错角相等
D.两条平行直线被第三条直线所截,同旁内角相等
4.如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=22°,则∠CEF等于( )
A.112° B.122° C.88° D.68°
5.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形ABC是三角板),其依据是( )
A.同旁内角互补,两直线平行
B.两直线平行,同旁内角互补
C.同位角相等,两直线平行
D.两直线平行,同位角相等
6.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.138° B.136° C.134° D.132°
7.下列选项中,可以用来说明命题“若|a|>3,则a>3”是假命题的反例是( )
A.a=﹣5 B.a=﹣3 C.a=﹣2 D.a=4
8.如图所示,图形中∠1与∠2不一定相等的是( )
A. B.
C. D.
9.如图,直线a与直线b、c都相交,若b∥c,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.140°
10.下列命题的逆命题是真命题的是( )
A.对顶角相等
B.同一三角形内等角对等边
C.同角的余角相等
D.全等三角形对应角相等
11.如图,AB∥CD,∠ABE=150°,∠BEF=70°,则∠DFE的度数为( )
A.30° B.40° C.50° D.60°
12.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:
①GH∥BC,②∠D=∠F,
③HE平分∠AHG,④DE⊥AB,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
13.如图,直线a,b被直线c所截,a∥b,∠1=42°13′,则∠2的度数为 .
14.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图.其中AB、CD都与地面l平行,∠BCD=60°,∠BAC=54°,当∠MAC为 度时.AM与CB平行.
15.用“举反例”的方法说明命题“若a2=b2,则a=b”是假命题时,这组反例可以是 .
16.如图,AB∥CD,已知平面内有一点N在直线AB与直线CD之间,且∠BND=30°,若∠NDC=α,则∠ABN= .(用含α的式子表示)
17.如图a∥b,则图中∠A,∠B,∠1,∠2的数量关系是 .
三.解答题(共5小题)
18.如图,已知:EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD.
19.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,求证:∠C=∠DBA.
20.如图,已知AB∥CD,一条直线分别交AB、CD于点E、F,∠EFB=∠B,FH⊥FB,点Q在BF上,连接QH.
(1)已知∠EFD=70°,直接写出∠HFG的度数;
(2)求证:FH平分∠GFD.
21.将一副直角三角板如图1摆放在直线MN上(直角三角板ABC和直角三角板EDC,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°),保持三角板EDC不动,将三角板ABC绕点C以每秒5°的速度顺时针旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.
(1)如图2,当AC为∠DCE的角平分线时,t= .
(2)当t=18时,求∠BCD的度数?
(3)在旋转过程中,当三角板ABC的AB边平行于三角板EDC的某一边时(不包含重合的情形),求此时t的值为 .(直接写出答案即可)
22.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.
(1)【基础问题】如图1,试说明:∠AGD=∠A+∠D.(完成下面的填空部分)
证明:过点G作直线MN∥AB,
∵AB∥CD,
∴① ∥CD.
∵MN∥AB,
∴② =∠MGA.
∵MN∥CD,
∴∠D=③ (④ ).
∴∠AGD=∠AGM+∠AGM=∠A+∠D.
(2)【类比探究】如图2,当点G在线段EF延长线上时,请写出∠AGD、∠A、∠D三者之间的数量关系,并说明理由.
(3)【应用拓展】如图3,点E与点A重合,AH平分∠GAB,且∠HDF=22°,∠AFC=72°,那么∠H的度数为 .
参考答案
一.选择题(共12小题)
1--10ABBAC CABAB 11--12BB
二.填空题(共5小题)
13.137°47′
14.66
15.a=1,b=﹣1(答案不唯一).
16.30°﹣α或330°﹣α.
17.∠ABD﹣∠1=∠CAB﹣∠2.
三.解答题(共5小题)
18.证明:过E点作AB∥EF,
∵AB∥EF,
∴∠APE=∠PEF(两直线平行,内错角相等),
∵EP⊥EQ,
∴∠PEQ=90°(垂直的定义),
即∠QEF+∠PEF=90°,
∴∠APE+∠QEF=90°,
∵∠EQC+∠APE=90°,
∴∠EQC=∠QEF,
∴EF∥CD(内错角相等,两直线平行),
∴AB∥CD(平行于同一直线的两直线互相平行).
19.证明:∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠DBA.
20.(1)解:AB∥CD,
∴∠B=∠BFD,
∵∠EFB=∠B,
∴∠BFD=∠EFB,
∵∠EFD=70°,
∴∠EFB=∠EFD=35°,
∵FH⊥FB,
∴∠HFQ=90°,
∴∠HFG=180°﹣∠EFB﹣∠HFQ=55°;
(2)证明:由(1)知∠BFD=∠EFB,∠HFQ=90°,
∴∠HFG+∠EFB=180°﹣∠HFQ=90°,∠DFH+∠BFD=90°,
∴∠HFG=∠DFH,
∴FH平分∠GFD.
21.解:(1)当AC为∠DCE的角平分线时,旋转角为15°,
∴t==3,
故答案为3.
(2)当t=18时,旋转角为90°,如图:
∵∠DCE=30°,∠ACB=45°,
∴∠ACD=60°,∠BCD=60°﹣45°=15°.
(3)当三角板ABC的AB边平行于三角板EDC的某一边时,有3种情况:
①当AB∥DE时,如图:
此时,BC与CD重合,
t=(30+40)÷5=15,
②当AB∥CE时,如图:
∵AB∥CE,
∴∠BCE=∠B=90°,
∴∠ACE=90°+45°=135°,
∴t=135÷5=27,
③当AB∥CD时,如图:
∵AB∥CD,
∴∠BCD=∠D=90°,
∴∠ACE=30°+90°+45°=165°,
∴t=165÷3=33.
综上所述,t=15或27或33.
22.解:(1)过点G作直线MN∥AB,
又∵AB∥CD,
∴MN∥CD(平行于同一条直线的两条直线平行),
∵MN∥AB,
∴∠A=∠AGM(两直线平行,内错角相等),
∵MN∥CD,
∴∠D=∠DGM(两直线平行,内错角相等),
∴∠AGD=∠AGM+∠DGM=∠A+∠D.
故答案为:MN;∠A;∠DGM;两直线平行,内错角相等.
(2)如图所示,过点G作直线MN∥AB,
又∵AB∥CD,
∴MN∥CD,
∵MN∥AB,
∴∠A=∠AGM,
∵MN∥CD,
∴∠D=∠DGM,
∴∠AGD=∠AGM﹣∠DGM=∠A﹣∠D.
(3)如图所示,
∵∠AFC=72°;
∴∠GAB=180°﹣72°=108°,
∵AH平分∠GAB,
∴∠HAB==54°,
∵DC∥AB,
∴∠HQC=54°,
∴∠H=∠HQC﹣∠HDF=54°﹣22°=32°
