人教版2024年七年级下册第5章《相交线与平行线》单元测试卷(含解析)
文档属性
| 名称 | 人教版2024年七年级下册第5章《相交线与平行线》单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 675.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-05 14:38:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2024年七年级下册第5章《相交线与平行线》单元测试卷
满分120分
一、选择题(共10题;共30分)
1.由图案①通过平移后可以得到的图案是( )
A. B. C. D.
2.若∠1与∠2是同旁内角,∠1=70°,则∠2 的度数为( )
A.110° B.70° C.20° D.无法确定
3.如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A.两点之间,线段最短 B.垂线段最短
C.两点确定一条直线 D.经过一点有且只有一条直线与已知直线垂直
4.下列语句,是真命题的是( )
A.对顶角相等 B.同位角相等
C.内错角相等 D.同旁内角互补
5.如图,下列说法中,不正确的是( )
A.∠1与∠3是对顶角 B.∠2与∠6是同位角
C.∠3 与∠4 是内错角 D.∠3 与∠5 是同旁内角
6.下列说法中,正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.同位角相等
C.从直线外一点到这条直线的垂线段叫做点到直线的距离
D.同一平面内,过一点有且只有一条直线与已知直线垂直
7.如图,已知AB∥CD,则图中与∠1相等的角有( )
A.5个 B.4个 C.3个 D.2个
8.如图,点 E 在 BC 的延长线上,对于给出的四个条件:
①∠1=∠3;②∠2+∠5=180°;③∠4=∠B;④∠D+∠BCD=180°.
其中能判定 AD∥BC的是( )
A.①② B.①④ C.①③ D.②④
9.如图,在三角形ABC中,BC=5.∠A=70°,∠B=75°,把三角形ABC沿直线BC的方向平移到三角形DEF的位置,若CF=3,则下列结论中,错误的是( )
A.BE=3 B.∠F= 35° C.DF=5 D.AB∥DE
10.将一个三角尺按如图所示的方式放置,∠ACB=90°,∠ABC=60°,点B,C分别在直线PQ,MN 上.若 PQ∥MN,∠ACM=44°,则∠PBC的度数为( )
A.46° B.44° C.22° D.20°
二、填空题(共6题;共24分)
11.“平行于同一条直线的两条直线平行”是 命题(填“真”或“假”).
12.如图,梯子的各条横档互相平行,若∠1=100°,则∠2= °.
13.若∠1和∠2是对顶角,∠1=36°,则∠2的补角是 .
14.如图,某住宅小区内有一长方形地块,现要在长方形地块内修筑同样宽的两条“之”字路,余下部分进行绿化.若道路的宽为 2m,则需要绿化的面积为 m .
15.如图,一条公路修到湖边时,需要弯折绕湖而过.若第一次弯折的角∠A=110°,第二次弯折的角∠B=145°,则第三次弯折的角∠C= °时,道路CE 恰好与AD 平行.
16.一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 .(填序号)
三、解答题(共8题;6+6+7+8+10+8+9+12=66分)
17.如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
18.如图,已知AB∥DE,EF∥BC,DE与BC相交于O,∠B=60°,求∠E的度数.
19.完成下面推理过程:
如图,已知∠1=∠2,,可推得.理由如下:
∵∠1=∠2( )
且( ),
∴(等量代换).
∴( ).
∴∠ ▲ =∠C( ).
又∵∠B=∠C(已知),
∴∠ ▲ =∠B(等量代换),
∴( ).
20.如图,把一张长方形纸片沿着直线 GF 折叠,∠CGF=30°,求∠1的度数.
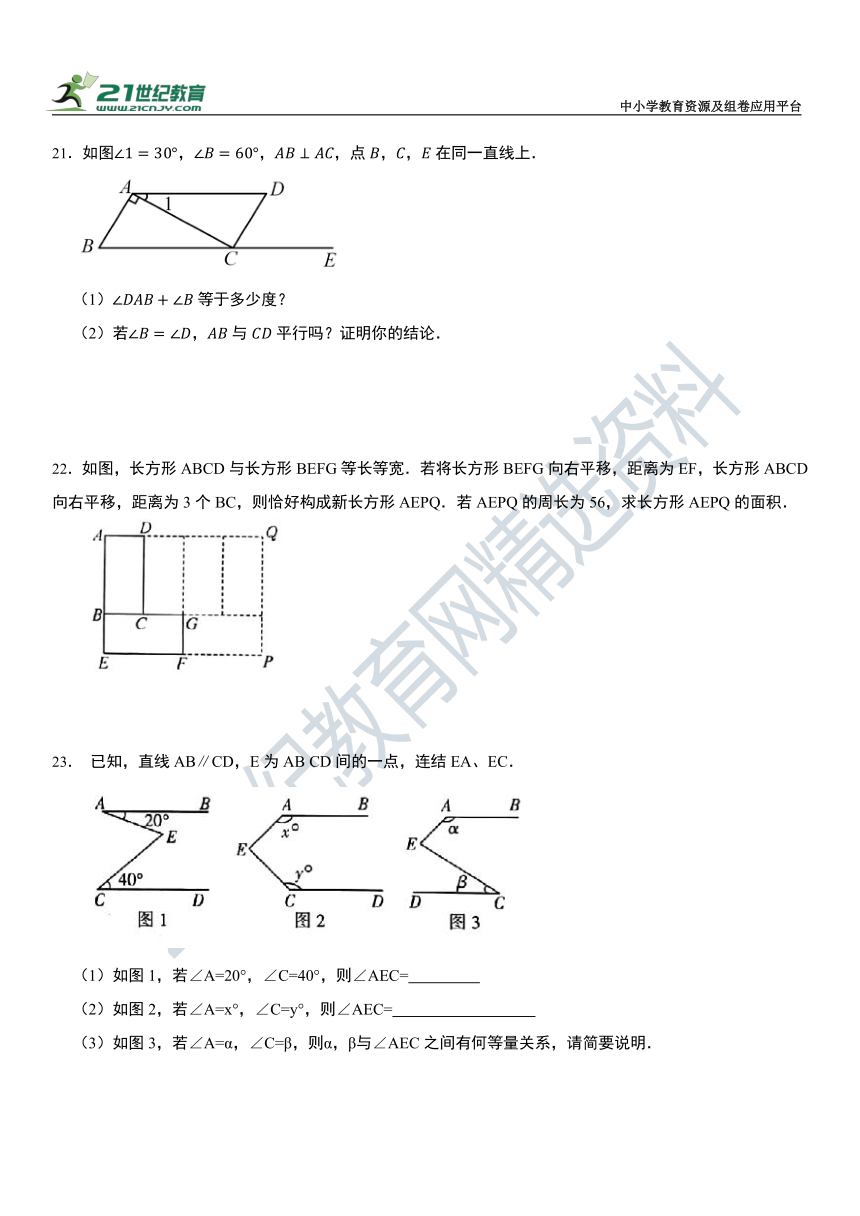
21.如图,,,点,,在同一直线上.
(1)等于多少度?
(2)若,与平行吗?证明你的结论.
22.如图,长方形ABCD与长方形BEFG等长等宽.若将长方形BEFG向右平移,距离为EF,长方形ABCD向右平移,距离为3个BC,则恰好构成新长方形AEPQ.若AEPQ的周长为56,求长方形AEPQ的面积.
23. 已知,直线AB∥CD,E为AB CD间的一点,连结EA、EC.
(1)如图1,若∠A=20°,∠C=40°,则∠AEC=
(2)如图2,若∠A=x°,∠C=y°,则∠AEC=
(3)如图3,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系,请简要说明.
24.如图,点分别在射线上,.
(1)求证:;
(2)如图1,点G、F在AE、BC上,连接EF、GC,且EF、GC相交于点H,∠AED=n∠AEF,∠BCD=n∠BCG,当∠DEH+∠DCH=2∠EHC时,求n的值.
(3)在(2)条件下,若,求证:.
答案与解析
1.D
【解析】解:A、该图改变了图形的形状,故不能通过平移得到,A不符合题意;
B、该图改变了图形的形状,故不能通过平移得到,B不符合题意;
C、该图改变了图形的形状,故不能通过平移得到,C不符合题意;
D、两图形状和大小没有变化,故能通过平移得到,D符合题意;
故答案为:D.
【点拨】根据图形的平移只改变图形的位置,不改变图形的形状和大小即可判断得出答案.
2.D
【解析】解:同旁内角只是一种位置关系,并没有一定的大小关系.
故答案为:D.
【点拨】只有两直线平行时同旁内角互补,两直线不平行时无法确定同旁内角的大小关系.
3.B
【解析】解:能符合题意解释这一现象的数学知识是垂线段最短,
故答案为:B.
【点拨】根据垂线段最短的性质求解即可。
4.A
【解析】A.对顶角相等,所以A选项为真命题;
B.两直线平行,同位角相等,所以B选项为假命题;
C.两直线平行,同错角相等,所以C选项为假命题;
D.两直线平行,同旁内角互补,所以D选项为假命题.
故答案为:A.
【点拨】真假命题的判断最简单的方法就是反证法,这也是解题的关键。
5.B
【解析】解:A.∠1和∠3是对顶角,A不符合题意;
B.∠2和∠6,既不是同位角,也不是内错角、同旁内角,B符合题意;
C.∠3与∠4是直线AB,直线CD,被直线EF所截,所得到的内错角,C不符合题意;
D.∠3与∠5是直线CD,直线DE,被直线EF所截所得到的同旁内角,D不符合题意;
故答案为:B.
【点拨】根据如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角进逐项行判断即可.
6.D
【解析】解:A、过直线外的一点有且只有一条直线与已知直线平行,故此选项错误,不符合题意;
B、两直线平行,同位角相等,故此选项错误,不符合题意;
C、从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故此选项错误,不符合题意;
D、同一平面内,过一点有且只有一条直线与已知直线垂直,故此选项正确,符合题意.
故答案为:D.
【点拨】根据经过直线外一点,有且只有一条直线与已知直线平行;两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补;从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;同一平面内,过一点有且只有一条直线与已知直线垂直进行判断求解即可.
7.C
【解析】解:如图,
∵AB∥CD,
∴∠1=∠3(二直线平行,同位角相等),
∵∠1=∠2,∠3=∠4(对顶角相等),
∴∠1=∠2=∠3=∠4,
∴图中与∠1相等得角有3个.
故答案为:C.
【点拨】由二直线平行,同位角相等,可得∠1=∠3,再由对顶角相等得∠1=∠2,∠3=∠4,从而可得答案.
8.B
【解析】解:①∵∴则符合题意;
②∵,∴则不符合题意;
③∵∴则不符合题意;
④∵∴则符合题意;
综上所述,可判断的有①④,
故答案为:B.
【点拨】根据平行线判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此逐项判断即可.
9.C
【解析】解:∵△ABC中, ∠A=70°,∠B=75° ,
∴∠ACB=180°-∠A-∠B=35°,
∵ △ABC沿直线BC的方向平移到△DEF的位置,且CF=3,
∴BE=CF=3,AB∥DE,∠F=∠ACB=35°,
故A、B、D三个选项都正确,不符合题意,只有C选项错误,符合题意.
故答案为:C.
【点拨】首先根据三角形的内角和定理算出∠ACB的度数,进而根据平移只会改变图形的位置,不会改变图形的形状、大小及方向,平移后对应点的连线相等且平行或在同一直线上,据此逐项判断得出答案.
10.A
【解析】解:∵PQ∥MN,
∴∠ACM=∠QPC=44°,
∵∠ABC=60°,
∴∠A=30°,
∴∠ABP=∠QPC-∠A=44°-30°=14°,
∴∠PBC=∠ABC-∠ABP=60°-14°=46°.
故答案为:A.
【点拨】根据两直线平行,内错角相等可得∠ACM=∠QPC=44°;根据三角形的外角等于与它不相邻的两个内角之和可得∠ABP=14°;即可求解.
11.真
【解析】解:根据平行公理可知“平行于同一直线的两直线互相平行”是真命题.故答案为:真.
【点拨】根据真命题的定义求解即可。
12.80
【解析】解:∵AB∥CD,
∴∠1=∠ABD=100°,
∴∠2=180°-∠ABD=180°-100°=80°,
故答案为:80.
【点拨】根据两直线平行,同位角相等可得∠1=∠ABD=100°,结合两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,叫做邻补角;一个角与它的邻补角的和等于180°即可求解.
13.144°
14.540
【解析】解:如图:
把两条”之”字路平移到长方形地块ABCD的最上边和最左边,余下部分EFGH是矩形;
则CF=32-2=30(米),CG=20-2=18(米),
∴矩形EFCG的面积=30×18=540(平方米);
故答案为:540.
【点拨】 把两条”之”字路平移到长方形地块的最上边和最左边,得出余下的部分是矩形,根据矩形的面积公式即可求解.
15.145
【解析】解:延长AB,EC,交于点F,如图:
∵AD∥EF,
∴∠F=∠A=110°;
∵∠FBC=180°-∠ABC=180°-145°=35°,
∴∠BCE=∠F+∠FBC=110°+35°=145°,
即第三次拐的角∠C=145°时,道路CE恰好与AD平行.
故答案为:145.
【点拨】延长AB,EC,交于点F,根据两直线平行,内错角相等可得∠F=∠A=110°;求出∠FBC=35°;根据三角形的外角等于与它不相邻的两个内角之和即可求解.
16.①③④
【解析】解:设AB与DE的交点为F
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,故①正确;
∵∠2=45°,∠E=60°,
∴∠EFB=∠E+∠2=105°,
∴∠EFB≠∠CAB,
∴AC与DE不平行,故②错误;
∵∠4=∠B=45°,∠C=45°,
∴∠4=∠C,
∴AC∥DE,故③正确;
当∠1=15°时, ∠2=90°-15°=75°,
∴∠EFB=∠E+∠2=60°+75°=135°.
∵∠B=45°,
∴∠B+∠EFB=180°,
∴BC∥DE,故④正确.
综上可得:①③④正确.
故答案为:①③④.
【点拨】设AB与DE的交点为F,根据同角的余角相等可判断①;由外角的性质可得∠EFB=∠E+∠2=105°,根据平行线的判定定理可判断②;根据∠4=∠B=45°,∠C=45°可得∠4=∠C,根据平行线的判定定理可判断③;由余角的性质可得 ∠2=90°-∠1=75°,根据外角的性质可得∠EFB=∠E+∠2=60°+75°=135°,则∠B+∠EFB=180°,据此判断④.
17.解:内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;
同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5;
同位角:∠3与∠7,∠2与∠8,∠4与∠6.
【点拨】根据两直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两边,可得内错角,根据两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角的位置相同,可得同位角.
18.解:∵AB∥DE, ∠B=60°
∴∠EOC=∠B=60°( 两直线平行,同位角相等),
∴∠BOD=∠EOC=60°(对顶角相等),
∵EF∥BC,
∴∠E=∠BOD=60°(两直线平行,同位角相等).
【点拨】由两直线平行,同位角相等,得∠EOC=∠B=60°,由对顶角相等得∠BOD=∠EOC=60°,进而再根据两直线平行,同位角相等,得∠E=∠BOD=60°.
19.解:∵∠1=∠2(已知)
且(对顶角相等),
∴(等量代换).
∴(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
又∵∠B=∠C(已知),
∴(等量代换),
∴(内错角相等,两直线平行).
20.解:如图:
∵把一张长方形纸带沿着直线GF折叠,∠CGF=30°,
∴∠EGF=∠FGC=30°,
∴∠FGC=∠EGF+∠FGC=60°,
∵AD∥BC,
∴∠FGC=∠2=60°,
∵GE∥FH,
∴∠1=∠2=60°.
【点拨】根据折叠前后两图形是全等图形,全等图形的对应角相等可得∠EGF=∠FGC=30°;求得∠FGC=60°;根据两直线平行同位角相等可得∠FGC=∠2=60°,根据两直线平行,同位角相等即可求解.
21.(1),
,
又,,
,
故等于度.
(2),
由(1)得:,
,
与平行.(同旁内角互补,两直线平行)
【点拨】(1) 由垂线的定义可得∠BAC=90°,结合已知可得:∠BAD+∠B=∠BAC+∠CAD+∠B=180°;
(2)结合(1)的结论和已知条件可得∠BAD+∠D=180°,根据同旁内角互补两直线平行可求解.
22.解:设AB=a,BC=b,
∵ 长方形ABCD向右平移,距离为3个BC,
∴DG=3b,
∴AQ=4b,
∵ 将长方形BEFG向右平移,距离为EF,
∴EF=FP,
∵ 长方形ABCD与长方形BEFG等长等宽 ,
∴EP=2EF=2a=4b,
∴a=2b,
∴AE=a+b=3b,
∵长方形AEPQ的周长为56,
∴2(AQ+AE)=56,
即2(4b+3b)=56,
∴b=4,
∴AQ=16,AE=12,
∴长方形AEPQ的面积为:AQ×AE=12×16=192.
【点拨】设AB=a,BC=b,由平移的性质得AQ=4b,EF=FP,结合长方形ABCD与长方形BEFG等长等宽可得EP=2EF=2a=4b,则a=2b,故AE=a+b=3b,进而根据长方形AEPQ的周长为56,建立方程可求出b的值,从而可求出AQ及AE的长,最后根据长方形面积计算方法可算出答案.
23.(1)60°
(2)360°-x°-y°
(3)α,β与∠AEC之间的等量关系为:∠AEC=180°-α+β
理由:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠C=∠CEF=β,
∴∠AEF=180°-α,
∵∠AEC=∠AEF+∠CEF=180°-α+β.
【解析】解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∠A=∠AEF=20°,∠C=∠CEF=40°,
∴∠AEC=∠AEF+∠CEF=20°+40°=60°.
故答案为:60°.
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠AEF=180°-x°,∠CEF=180°-y°,
∴∠AEC=∠AEF+∠CEF=180°-x°+180°-y°=360°-x°-y°.
故答案为:360°-x°-y°.
【点拨】分别过点E作其中一条直线的平行线,再根据平行线的性质,求出某个角的度数或某些角之间的数量关系.
24.(1)证明:过点D作DM∥AM,
;
(2)解:由题意可得:设,则
过点H在右侧作HQ∥AM
;
(3)证明:由(2),得
.
【点拨】(1)过点D作DM∥AM,由二直线平行,内错角相等得∠MED=∠EDP,然后根据角的和差及已知条件可推出∠NCD=∠PDC,由内错角相等,两直线平行得DP∥BC,进而根据平行于同一直线的两条直线互相平行得AM∥BN;
(2)设,则,,,过点H在右侧作HQ∥AM,由平行于同一直线的两条直线互相平行得HQ∥BN,由平行线的性质及角的和差可得,进而根据∠DEH+∠DCH=2∠EHC建立方程可求出n的值;
(3)由(2)可得,则,根据平角定义及等式性质可推出∠MED+∠NCD=∠EDC=90°,从而根据垂直的定义得出结论.
人教版2024年七年级下册第5章《相交线与平行线》单元测试卷
满分120分
一、选择题(共10题;共30分)
1.由图案①通过平移后可以得到的图案是( )
A. B. C. D.
2.若∠1与∠2是同旁内角,∠1=70°,则∠2 的度数为( )
A.110° B.70° C.20° D.无法确定
3.如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
A.两点之间,线段最短 B.垂线段最短
C.两点确定一条直线 D.经过一点有且只有一条直线与已知直线垂直
4.下列语句,是真命题的是( )
A.对顶角相等 B.同位角相等
C.内错角相等 D.同旁内角互补
5.如图,下列说法中,不正确的是( )
A.∠1与∠3是对顶角 B.∠2与∠6是同位角
C.∠3 与∠4 是内错角 D.∠3 与∠5 是同旁内角
6.下列说法中,正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.同位角相等
C.从直线外一点到这条直线的垂线段叫做点到直线的距离
D.同一平面内,过一点有且只有一条直线与已知直线垂直
7.如图,已知AB∥CD,则图中与∠1相等的角有( )
A.5个 B.4个 C.3个 D.2个
8.如图,点 E 在 BC 的延长线上,对于给出的四个条件:
①∠1=∠3;②∠2+∠5=180°;③∠4=∠B;④∠D+∠BCD=180°.
其中能判定 AD∥BC的是( )
A.①② B.①④ C.①③ D.②④
9.如图,在三角形ABC中,BC=5.∠A=70°,∠B=75°,把三角形ABC沿直线BC的方向平移到三角形DEF的位置,若CF=3,则下列结论中,错误的是( )
A.BE=3 B.∠F= 35° C.DF=5 D.AB∥DE
10.将一个三角尺按如图所示的方式放置,∠ACB=90°,∠ABC=60°,点B,C分别在直线PQ,MN 上.若 PQ∥MN,∠ACM=44°,则∠PBC的度数为( )
A.46° B.44° C.22° D.20°
二、填空题(共6题;共24分)
11.“平行于同一条直线的两条直线平行”是 命题(填“真”或“假”).
12.如图,梯子的各条横档互相平行,若∠1=100°,则∠2= °.
13.若∠1和∠2是对顶角,∠1=36°,则∠2的补角是 .
14.如图,某住宅小区内有一长方形地块,现要在长方形地块内修筑同样宽的两条“之”字路,余下部分进行绿化.若道路的宽为 2m,则需要绿化的面积为 m .
15.如图,一条公路修到湖边时,需要弯折绕湖而过.若第一次弯折的角∠A=110°,第二次弯折的角∠B=145°,则第三次弯折的角∠C= °时,道路CE 恰好与AD 平行.
16.一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 .(填序号)
三、解答题(共8题;6+6+7+8+10+8+9+12=66分)
17.如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.
18.如图,已知AB∥DE,EF∥BC,DE与BC相交于O,∠B=60°,求∠E的度数.
19.完成下面推理过程:
如图,已知∠1=∠2,,可推得.理由如下:
∵∠1=∠2( )
且( ),
∴(等量代换).
∴( ).
∴∠ ▲ =∠C( ).
又∵∠B=∠C(已知),
∴∠ ▲ =∠B(等量代换),
∴( ).
20.如图,把一张长方形纸片沿着直线 GF 折叠,∠CGF=30°,求∠1的度数.
21.如图,,,点,,在同一直线上.
(1)等于多少度?
(2)若,与平行吗?证明你的结论.
22.如图,长方形ABCD与长方形BEFG等长等宽.若将长方形BEFG向右平移,距离为EF,长方形ABCD向右平移,距离为3个BC,则恰好构成新长方形AEPQ.若AEPQ的周长为56,求长方形AEPQ的面积.
23. 已知,直线AB∥CD,E为AB CD间的一点,连结EA、EC.
(1)如图1,若∠A=20°,∠C=40°,则∠AEC=
(2)如图2,若∠A=x°,∠C=y°,则∠AEC=
(3)如图3,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系,请简要说明.
24.如图,点分别在射线上,.
(1)求证:;
(2)如图1,点G、F在AE、BC上,连接EF、GC,且EF、GC相交于点H,∠AED=n∠AEF,∠BCD=n∠BCG,当∠DEH+∠DCH=2∠EHC时,求n的值.
(3)在(2)条件下,若,求证:.
答案与解析
1.D
【解析】解:A、该图改变了图形的形状,故不能通过平移得到,A不符合题意;
B、该图改变了图形的形状,故不能通过平移得到,B不符合题意;
C、该图改变了图形的形状,故不能通过平移得到,C不符合题意;
D、两图形状和大小没有变化,故能通过平移得到,D符合题意;
故答案为:D.
【点拨】根据图形的平移只改变图形的位置,不改变图形的形状和大小即可判断得出答案.
2.D
【解析】解:同旁内角只是一种位置关系,并没有一定的大小关系.
故答案为:D.
【点拨】只有两直线平行时同旁内角互补,两直线不平行时无法确定同旁内角的大小关系.
3.B
【解析】解:能符合题意解释这一现象的数学知识是垂线段最短,
故答案为:B.
【点拨】根据垂线段最短的性质求解即可。
4.A
【解析】A.对顶角相等,所以A选项为真命题;
B.两直线平行,同位角相等,所以B选项为假命题;
C.两直线平行,同错角相等,所以C选项为假命题;
D.两直线平行,同旁内角互补,所以D选项为假命题.
故答案为:A.
【点拨】真假命题的判断最简单的方法就是反证法,这也是解题的关键。
5.B
【解析】解:A.∠1和∠3是对顶角,A不符合题意;
B.∠2和∠6,既不是同位角,也不是内错角、同旁内角,B符合题意;
C.∠3与∠4是直线AB,直线CD,被直线EF所截,所得到的内错角,C不符合题意;
D.∠3与∠5是直线CD,直线DE,被直线EF所截所得到的同旁内角,D不符合题意;
故答案为:B.
【点拨】根据如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角进逐项行判断即可.
6.D
【解析】解:A、过直线外的一点有且只有一条直线与已知直线平行,故此选项错误,不符合题意;
B、两直线平行,同位角相等,故此选项错误,不符合题意;
C、从直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故此选项错误,不符合题意;
D、同一平面内,过一点有且只有一条直线与已知直线垂直,故此选项正确,符合题意.
故答案为:D.
【点拨】根据经过直线外一点,有且只有一条直线与已知直线平行;两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补;从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;同一平面内,过一点有且只有一条直线与已知直线垂直进行判断求解即可.
7.C
【解析】解:如图,
∵AB∥CD,
∴∠1=∠3(二直线平行,同位角相等),
∵∠1=∠2,∠3=∠4(对顶角相等),
∴∠1=∠2=∠3=∠4,
∴图中与∠1相等得角有3个.
故答案为:C.
【点拨】由二直线平行,同位角相等,可得∠1=∠3,再由对顶角相等得∠1=∠2,∠3=∠4,从而可得答案.
8.B
【解析】解:①∵∴则符合题意;
②∵,∴则不符合题意;
③∵∴则不符合题意;
④∵∴则符合题意;
综上所述,可判断的有①④,
故答案为:B.
【点拨】根据平行线判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此逐项判断即可.
9.C
【解析】解:∵△ABC中, ∠A=70°,∠B=75° ,
∴∠ACB=180°-∠A-∠B=35°,
∵ △ABC沿直线BC的方向平移到△DEF的位置,且CF=3,
∴BE=CF=3,AB∥DE,∠F=∠ACB=35°,
故A、B、D三个选项都正确,不符合题意,只有C选项错误,符合题意.
故答案为:C.
【点拨】首先根据三角形的内角和定理算出∠ACB的度数,进而根据平移只会改变图形的位置,不会改变图形的形状、大小及方向,平移后对应点的连线相等且平行或在同一直线上,据此逐项判断得出答案.
10.A
【解析】解:∵PQ∥MN,
∴∠ACM=∠QPC=44°,
∵∠ABC=60°,
∴∠A=30°,
∴∠ABP=∠QPC-∠A=44°-30°=14°,
∴∠PBC=∠ABC-∠ABP=60°-14°=46°.
故答案为:A.
【点拨】根据两直线平行,内错角相等可得∠ACM=∠QPC=44°;根据三角形的外角等于与它不相邻的两个内角之和可得∠ABP=14°;即可求解.
11.真
【解析】解:根据平行公理可知“平行于同一直线的两直线互相平行”是真命题.故答案为:真.
【点拨】根据真命题的定义求解即可。
12.80
【解析】解:∵AB∥CD,
∴∠1=∠ABD=100°,
∴∠2=180°-∠ABD=180°-100°=80°,
故答案为:80.
【点拨】根据两直线平行,同位角相等可得∠1=∠ABD=100°,结合两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,叫做邻补角;一个角与它的邻补角的和等于180°即可求解.
13.144°
14.540
【解析】解:如图:
把两条”之”字路平移到长方形地块ABCD的最上边和最左边,余下部分EFGH是矩形;
则CF=32-2=30(米),CG=20-2=18(米),
∴矩形EFCG的面积=30×18=540(平方米);
故答案为:540.
【点拨】 把两条”之”字路平移到长方形地块的最上边和最左边,得出余下的部分是矩形,根据矩形的面积公式即可求解.
15.145
【解析】解:延长AB,EC,交于点F,如图:
∵AD∥EF,
∴∠F=∠A=110°;
∵∠FBC=180°-∠ABC=180°-145°=35°,
∴∠BCE=∠F+∠FBC=110°+35°=145°,
即第三次拐的角∠C=145°时,道路CE恰好与AD平行.
故答案为:145.
【点拨】延长AB,EC,交于点F,根据两直线平行,内错角相等可得∠F=∠A=110°;求出∠FBC=35°;根据三角形的外角等于与它不相邻的两个内角之和即可求解.
16.①③④
【解析】解:设AB与DE的交点为F
∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,故①正确;
∵∠2=45°,∠E=60°,
∴∠EFB=∠E+∠2=105°,
∴∠EFB≠∠CAB,
∴AC与DE不平行,故②错误;
∵∠4=∠B=45°,∠C=45°,
∴∠4=∠C,
∴AC∥DE,故③正确;
当∠1=15°时, ∠2=90°-15°=75°,
∴∠EFB=∠E+∠2=60°+75°=135°.
∵∠B=45°,
∴∠B+∠EFB=180°,
∴BC∥DE,故④正确.
综上可得:①③④正确.
故答案为:①③④.
【点拨】设AB与DE的交点为F,根据同角的余角相等可判断①;由外角的性质可得∠EFB=∠E+∠2=105°,根据平行线的判定定理可判断②;根据∠4=∠B=45°,∠C=45°可得∠4=∠C,根据平行线的判定定理可判断③;由余角的性质可得 ∠2=90°-∠1=75°,根据外角的性质可得∠EFB=∠E+∠2=60°+75°=135°,则∠B+∠EFB=180°,据此判断④.
17.解:内错角:∠1与∠4,∠3与∠5,∠2与∠6,∠4与∠8;
同旁内角:∠3与∠6,∠2与∠5,∠2与∠4,∠4与∠5;
同位角:∠3与∠7,∠2与∠8,∠4与∠6.
【点拨】根据两直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两边,可得内错角,根据两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角的位置相同,可得同位角.
18.解:∵AB∥DE, ∠B=60°
∴∠EOC=∠B=60°( 两直线平行,同位角相等),
∴∠BOD=∠EOC=60°(对顶角相等),
∵EF∥BC,
∴∠E=∠BOD=60°(两直线平行,同位角相等).
【点拨】由两直线平行,同位角相等,得∠EOC=∠B=60°,由对顶角相等得∠BOD=∠EOC=60°,进而再根据两直线平行,同位角相等,得∠E=∠BOD=60°.
19.解:∵∠1=∠2(已知)
且(对顶角相等),
∴(等量代换).
∴(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
又∵∠B=∠C(已知),
∴(等量代换),
∴(内错角相等,两直线平行).
20.解:如图:
∵把一张长方形纸带沿着直线GF折叠,∠CGF=30°,
∴∠EGF=∠FGC=30°,
∴∠FGC=∠EGF+∠FGC=60°,
∵AD∥BC,
∴∠FGC=∠2=60°,
∵GE∥FH,
∴∠1=∠2=60°.
【点拨】根据折叠前后两图形是全等图形,全等图形的对应角相等可得∠EGF=∠FGC=30°;求得∠FGC=60°;根据两直线平行同位角相等可得∠FGC=∠2=60°,根据两直线平行,同位角相等即可求解.
21.(1),
,
又,,
,
故等于度.
(2),
由(1)得:,
,
与平行.(同旁内角互补,两直线平行)
【点拨】(1) 由垂线的定义可得∠BAC=90°,结合已知可得:∠BAD+∠B=∠BAC+∠CAD+∠B=180°;
(2)结合(1)的结论和已知条件可得∠BAD+∠D=180°,根据同旁内角互补两直线平行可求解.
22.解:设AB=a,BC=b,
∵ 长方形ABCD向右平移,距离为3个BC,
∴DG=3b,
∴AQ=4b,
∵ 将长方形BEFG向右平移,距离为EF,
∴EF=FP,
∵ 长方形ABCD与长方形BEFG等长等宽 ,
∴EP=2EF=2a=4b,
∴a=2b,
∴AE=a+b=3b,
∵长方形AEPQ的周长为56,
∴2(AQ+AE)=56,
即2(4b+3b)=56,
∴b=4,
∴AQ=16,AE=12,
∴长方形AEPQ的面积为:AQ×AE=12×16=192.
【点拨】设AB=a,BC=b,由平移的性质得AQ=4b,EF=FP,结合长方形ABCD与长方形BEFG等长等宽可得EP=2EF=2a=4b,则a=2b,故AE=a+b=3b,进而根据长方形AEPQ的周长为56,建立方程可求出b的值,从而可求出AQ及AE的长,最后根据长方形面积计算方法可算出答案.
23.(1)60°
(2)360°-x°-y°
(3)α,β与∠AEC之间的等量关系为:∠AEC=180°-α+β
理由:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠C=∠CEF=β,
∴∠AEF=180°-α,
∵∠AEC=∠AEF+∠CEF=180°-α+β.
【解析】解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∠A=∠AEF=20°,∠C=∠CEF=40°,
∴∠AEC=∠AEF+∠CEF=20°+40°=60°.
故答案为:60°.
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠AEF=180°-x°,∠CEF=180°-y°,
∴∠AEC=∠AEF+∠CEF=180°-x°+180°-y°=360°-x°-y°.
故答案为:360°-x°-y°.
【点拨】分别过点E作其中一条直线的平行线,再根据平行线的性质,求出某个角的度数或某些角之间的数量关系.
24.(1)证明:过点D作DM∥AM,
;
(2)解:由题意可得:设,则
过点H在右侧作HQ∥AM
;
(3)证明:由(2),得
.
【点拨】(1)过点D作DM∥AM,由二直线平行,内错角相等得∠MED=∠EDP,然后根据角的和差及已知条件可推出∠NCD=∠PDC,由内错角相等,两直线平行得DP∥BC,进而根据平行于同一直线的两条直线互相平行得AM∥BN;
(2)设,则,,,过点H在右侧作HQ∥AM,由平行于同一直线的两条直线互相平行得HQ∥BN,由平行线的性质及角的和差可得,进而根据∠DEH+∠DCH=2∠EHC建立方程可求出n的值;
(3)由(2)可得,则,根据平角定义及等式性质可推出∠MED+∠NCD=∠EDC=90°,从而根据垂直的定义得出结论.
