数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 453.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-05 16:51:46 | ||
图片预览






文档简介
(共22张PPT)
直线与圆的位置关系
点到直线的距离公式,圆的标准方程和一般方程分别是什么?
旧知复习
一艘轮船在沿直线返回港口的
途中,接到气象台的台风预报:
台风中心位于轮船正西70 km处,
受影响的范围是半径长为30km的
圆形区域. 已知港口位于台风中心
正北40 km处,如果这艘轮船不改变
航线,那么它是否会受到台风的影响?
轮船
港口
台风
课堂探究
新课学习
下面我们以太阳的起落为例.以蓝线为水平线,圆圈为太阳!
注意观察!!
课堂探究
新课学习
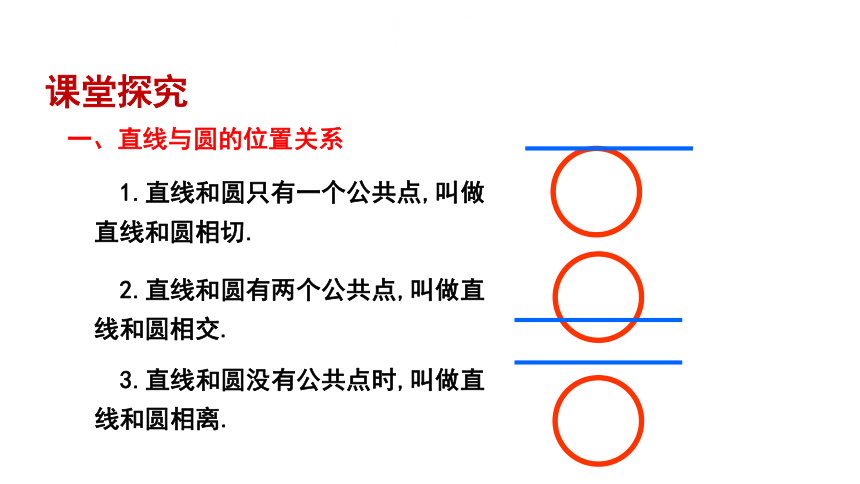
1.直线和圆只有一个公共点,叫做直线和圆相切.
2.直线和圆有两个公共点,叫做直线和圆相交.
3.直线和圆没有公共点时,叫做直线和圆相离.
一、直线与圆的位置关系
课堂探究
新课学习
.
o
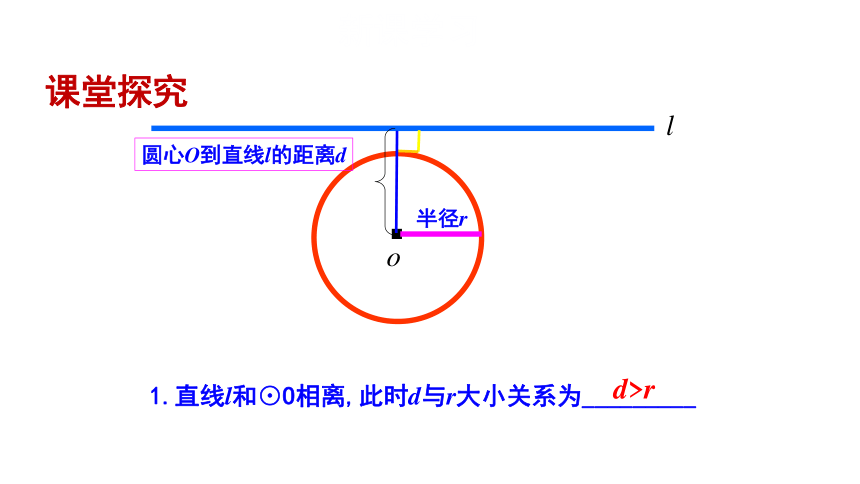
圆心O到直线l的距离d
l
半径r
1.直线l和⊙O相离,此时d与r大小关系为_________
d>r
课堂探究
新课学习
l
.
o
圆心O到直线l的距离d
半径r
2.直线l和⊙O相切,此时d与r大小关系为_________
d=r
课堂探究
新课学习
.
o
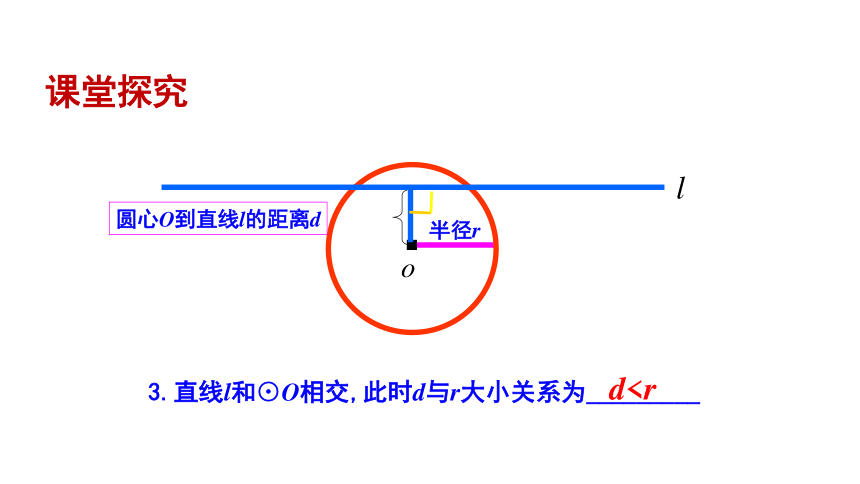
圆心O到直线l的距离d
半径r
3.直线l和⊙O相交,此时d与r大小关系为_________
l
d课堂探究
新课学习
1.利用圆心到直线的距离d与半径r的大小关系判断:
二、直线与圆的位置关系的判定方法:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
直线l:Ax+By+C=0,圆O:(x-a)2+(y-b)2=r2(r>0)
课堂探究
新课学习
2.利用直线与圆的公共点的个数进行判断:
直线与圆相离
直线与圆相切
直线与圆相交
n=0
n=1
n=2
△<0
△=0
△>0
课堂探究
新课学习
例1 如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们交点的坐标.
.
x
y
O
C
A
B
l
典型例题
新课学习
解法一:
(代数法)由直线l与圆的方程,得
消去 ,得
因为
所以直线l与圆相交,有两个公共点.
新课学习
解法二:
其圆心C的坐标为(0,1),半径长为 ,
点C(0,1)到直线l的距离
所以直线l与圆相交,有两个公共点.
由
解得
把x1=2代入方程①,得y1=0;把x2=1代入方程①, 得y2=3.
所以直线l与圆有两个交点,它们的坐标分别是A(2,0),B(1,3).
(几何法)
新课学习
1.设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,则a的值为( )
A.± B.±2 C.±2 D.±4
【解析】选B.由已知,可知直线方程为y=x+a,
即x-y+a=0,所以有 ,得a=±2.
变式练习
新课学习
例2 已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0
所截得的弦长为 ,求直线l的方程.
典型例题
新课学习
解:将圆的方程写成标准形式x2+(y+2)2=25,得圆心坐标是(0,-2),半径长r=5.
如图,因为直线l被圆所截得的弦长是 ,所以弦心距为 ,即圆心到所求直线l的距离为 .
因为直线l过点M(-3,-3),所以可设所求直线l的方程为
y+3=k(x+3),即kx-y+3k-3=0.
根据点到直线的距离公式,得到圆心到直线l的距离
因此,
典型例题
新课学习
即
两边平方,并整理得到 2k2-3k-2=0,
解得k= ,或k=2.
所以所求直线l有两条,它们的方程分别为
y+3= (x+3),或 y+3=2(x+3).
即x+2y+9=0,或2x-y+3=0.
新课学习
直线x+ y=0绕原点按顺时针方向旋转30°所得直线与圆x2+y2-4x+1=0的位置关系是( )
A.直线与圆相切 B.直线与圆相交但不过圆心
C.直线与圆相离 D.直线过圆心
A
变式练习
新课学习
解:选A.因为直线x+ y=0的倾斜角为150°,所以顺时针方向旋转30°后的倾斜角为120°,
旋转后的直线方程为x+y=0.
将圆的方程化为(x-2)2+y2=3,
所以圆心的坐标为(2,0),半径为 ,圆心到直线x+y=0的距离为 =圆的半径,
所以直线和圆相切.
新课学习
直线Ax+By+C=0(A,B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
dd=r
d>r
d与r
2个
1个
0个
交点个数
图形
相交
相切
相离
位置
r
d
r
d
r
d
则有以下关系:
课堂小结
求圆心坐标及半径r(配方法)
圆心到直线的距离d (点到直线距离公式)
消去y
判断直线和圆的位置关系
几何方法
代数方法
课堂小结
再见
直线与圆的位置关系
点到直线的距离公式,圆的标准方程和一般方程分别是什么?
旧知复习
一艘轮船在沿直线返回港口的
途中,接到气象台的台风预报:
台风中心位于轮船正西70 km处,
受影响的范围是半径长为30km的
圆形区域. 已知港口位于台风中心
正北40 km处,如果这艘轮船不改变
航线,那么它是否会受到台风的影响?
轮船
港口
台风
课堂探究
新课学习
下面我们以太阳的起落为例.以蓝线为水平线,圆圈为太阳!
注意观察!!
课堂探究
新课学习
1.直线和圆只有一个公共点,叫做直线和圆相切.
2.直线和圆有两个公共点,叫做直线和圆相交.
3.直线和圆没有公共点时,叫做直线和圆相离.
一、直线与圆的位置关系
课堂探究
新课学习
.
o
圆心O到直线l的距离d
l
半径r
1.直线l和⊙O相离,此时d与r大小关系为_________
d>r
课堂探究
新课学习
l
.
o
圆心O到直线l的距离d
半径r
2.直线l和⊙O相切,此时d与r大小关系为_________
d=r
课堂探究
新课学习
.
o
圆心O到直线l的距离d
半径r
3.直线l和⊙O相交,此时d与r大小关系为_________
l
d
新课学习
1.利用圆心到直线的距离d与半径r的大小关系判断:
二、直线与圆的位置关系的判定方法:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
直线l:Ax+By+C=0,圆O:(x-a)2+(y-b)2=r2(r>0)
课堂探究
新课学习
2.利用直线与圆的公共点的个数进行判断:
直线与圆相离
直线与圆相切
直线与圆相交
n=0
n=1
n=2
△<0
△=0
△>0
课堂探究
新课学习
例1 如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们交点的坐标.
.
x
y
O
C
A
B
l
典型例题
新课学习
解法一:
(代数法)由直线l与圆的方程,得
消去 ,得
因为
所以直线l与圆相交,有两个公共点.
新课学习
解法二:
其圆心C的坐标为(0,1),半径长为 ,
点C(0,1)到直线l的距离
所以直线l与圆相交,有两个公共点.
由
解得
把x1=2代入方程①,得y1=0;把x2=1代入方程①, 得y2=3.
所以直线l与圆有两个交点,它们的坐标分别是A(2,0),B(1,3).
(几何法)
新课学习
1.设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,则a的值为( )
A.± B.±2 C.±2 D.±4
【解析】选B.由已知,可知直线方程为y=x+a,
即x-y+a=0,所以有 ,得a=±2.
变式练习
新课学习
例2 已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0
所截得的弦长为 ,求直线l的方程.
典型例题
新课学习
解:将圆的方程写成标准形式x2+(y+2)2=25,得圆心坐标是(0,-2),半径长r=5.
如图,因为直线l被圆所截得的弦长是 ,所以弦心距为 ,即圆心到所求直线l的距离为 .
因为直线l过点M(-3,-3),所以可设所求直线l的方程为
y+3=k(x+3),即kx-y+3k-3=0.
根据点到直线的距离公式,得到圆心到直线l的距离
因此,
典型例题
新课学习
即
两边平方,并整理得到 2k2-3k-2=0,
解得k= ,或k=2.
所以所求直线l有两条,它们的方程分别为
y+3= (x+3),或 y+3=2(x+3).
即x+2y+9=0,或2x-y+3=0.
新课学习
直线x+ y=0绕原点按顺时针方向旋转30°所得直线与圆x2+y2-4x+1=0的位置关系是( )
A.直线与圆相切 B.直线与圆相交但不过圆心
C.直线与圆相离 D.直线过圆心
A
变式练习
新课学习
解:选A.因为直线x+ y=0的倾斜角为150°,所以顺时针方向旋转30°后的倾斜角为120°,
旋转后的直线方程为x+y=0.
将圆的方程化为(x-2)2+y2=3,
所以圆心的坐标为(2,0),半径为 ,圆心到直线x+y=0的距离为 =圆的半径,
所以直线和圆相切.
新课学习
直线Ax+By+C=0(A,B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
d
d>r
d与r
2个
1个
0个
交点个数
图形
相交
相切
相离
位置
r
d
r
d
r
d
则有以下关系:
课堂小结
求圆心坐标及半径r(配方法)
圆心到直线的距离d (点到直线距离公式)
消去y
判断直线和圆的位置关系
几何方法
代数方法
课堂小结
再见
