1.4.2用空间向量研究夹角问题 课件(共23张ppt) 数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.2用空间向量研究夹角问题 课件(共23张ppt) 数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 936.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-05 16:53:38 | ||
图片预览




文档简介
(共23张PPT)
用空间向量研究距离、夹角问题
环节二 用向量方法研究夹角问题
引入新课
用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中所涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
课堂探究
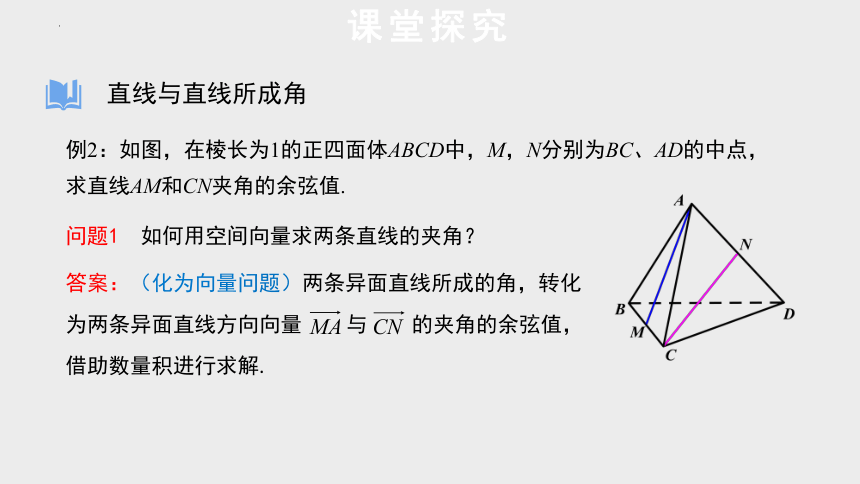
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
问题1 如何用空间向量求两条直线的夹角?
答案:(化为向量问题)两条异面直线所成的角,转化为两条异面直线方向向量 与 的夹角的余弦值,借助数量积进行求解.
直线与直线所成角
课堂探究
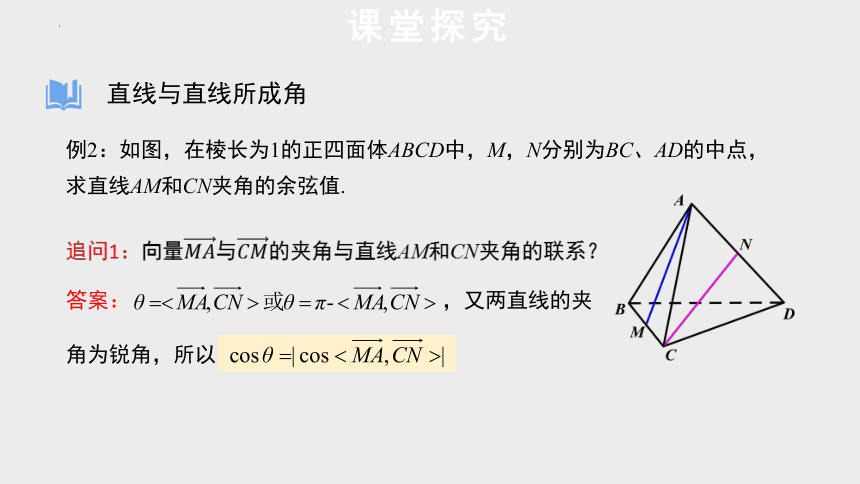
追问1:向量与的夹角与直线AM和CN夹角的联系?
答案: ,又两直线的夹角为锐角,所以
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
直线与直线所成角
课堂探究
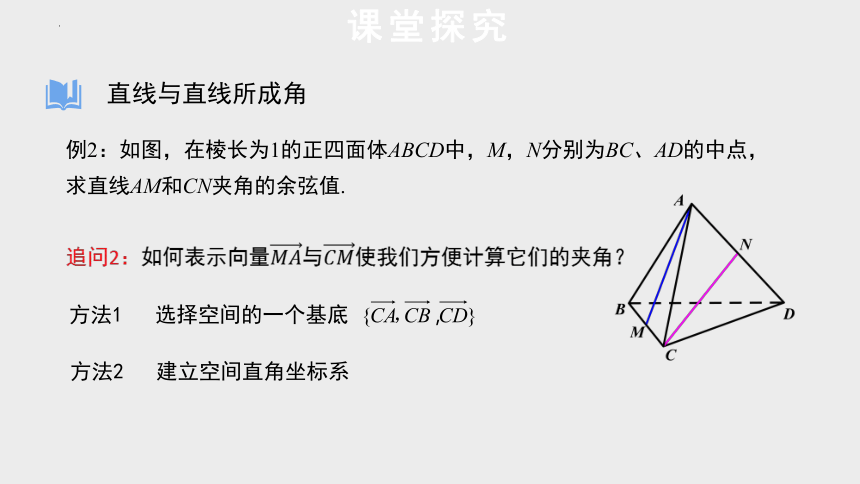
追问2:如何表示向量与使我们方便计算它们的夹角?
方法2 建立空间直角坐标系
方法1 选择空间的一个基底
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
直线与直线所成角
课堂探究
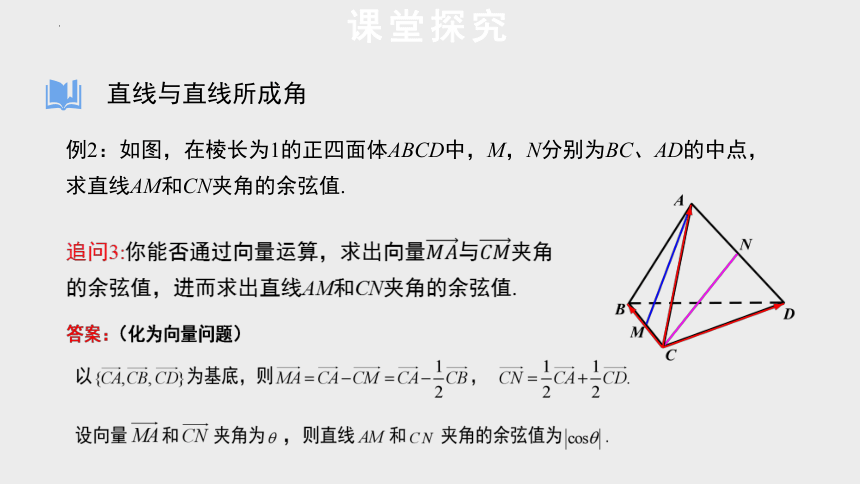
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
直线与直线所成角
追问3:你能否通过向量运算,求出向量与夹角的余弦值,进而求出直线AM和CN夹角的余弦值.
课堂探究
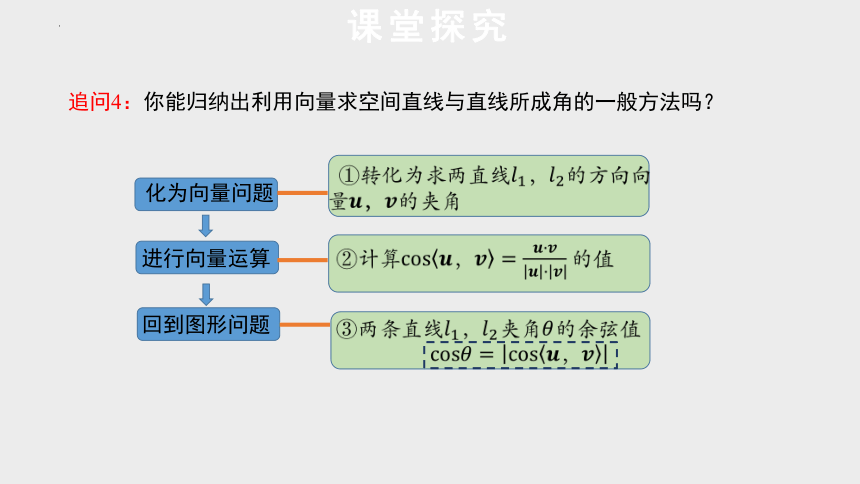
追问4:你能归纳出利用向量求空间直线与直线所成角的一般方法吗?
课堂探究
化为向量问题
进行向量运算
回到图形问题
课堂探究
直线与平面所成角
问题2:斜线与平面所成的角的定义是什么?
答案:平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角;一条直线垂直于平面,它们所成的角是90o;一条直线和平面平行,或在平面内,它们所成的角是0o.直线与平面所成角的范围:
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
课堂探究
直线与平面所成角
追问:你能根据定义做出线面角吗?
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
答案:过直线上一点A,做平面α的垂线交平面α于点C,联接BC,∠ABC即为直线AB与平面α所成的角.
课堂探究
直线与平面所成角
问题3:这个问题的已知条件是什么?如何将几何问题
转化为向量问题?
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
答案:已知一条直线和一个平面,我们用一个点和方向向量表示直线,用一个点和法向量表示平面.因此,我们借助直线AB的方向向量u与平面α的法向量n的夹角表示直线AB与平面α所成的角的大小.
课堂探究
直线与平面所成角
追问:如何借助直线的方向向量u与平面的法向量n求直线和平面的夹角?
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
课堂探究
直线与平面所成角
小结:
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
课堂探究
两相交平面所成角
问题4:类比已有的直线、平面所成角的定义,你认为合理定义两个平面所成的角?
答案:平面与平面相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面与平面的夹角.
追问1:你能说说平面与平面的夹角与二面角的区别与联系吗?
答案:二面角的大小是指其两个半平面的张开程度,可以用其平面角的大小来定义,它的取值范围是 ;而平面与平面的夹角是指平面与平面相交,形成的四个二面角中不大于90o的二面角,它的取值范围是 .
课堂探究
两相交平面所成角
追问2:角度是度量方向差异的量,那么决定平面方向的是什么?
答案:在空间向量里,通过一个点和法向量可以确定唯一的平面.
问题4:类比已有的直线、平面所成角的定义,你认为合理定义两个平面所成的角?
追问1:你能说说平面与平面的夹角与二面角的区别与联系吗?
课堂探究
两相交平面所成角
问题5:两个平面的法向量夹角与两个面夹角的关系?
答案:若平面与平面的法向量为n1,n2,则平面与平面的夹角即为向量为n1,n2的夹角或其补角.
课堂探究
两相交平面所成角
追问:为何向量夹角余弦值的绝对值为两个平面夹角的余弦值?
问题6:如何借助平面与平面的法向量为n1,n2求两个平面的夹角?
答案:
知识应用
例题讲解
例3: 如图,直棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1. 求平面PQR与平面A1B1C1夹角的余弦值.
分析:平面PQR与平面A1B1C1夹角可以转化为平面PQR与平面A1B1C1法向量的夹角,所以只需建立恰当的直角坐标系求出两个平面的法向量的夹角即可.
知识应用
例题讲解
解:
(化为向量问题)
以C1为坐标原点,C1A1,C1B1,C1C所在直线为x轴、y轴、z轴建立空间直角坐标系,设平面A1B1C1法向量为n1,平面PQR法向量为n2,平面PQR与平面A1B1C1夹角即为n1,n2的夹角或其补角.
例3: 如图,直棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1. 求平面PQR与平面A1B1C1夹角的余弦值.
知识应用
例题讲解
知识应用
例题讲解
归纳小结
本节课学习了什么内容?
异面直线夹角、线面角、两平面夹角的向量表示;
用向量方法解决立体几何问题的一般步骤.
再 见
用空间向量研究距离、夹角问题
环节二 用向量方法研究夹角问题
引入新课
用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中所涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
课堂探究
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
问题1 如何用空间向量求两条直线的夹角?
答案:(化为向量问题)两条异面直线所成的角,转化为两条异面直线方向向量 与 的夹角的余弦值,借助数量积进行求解.
直线与直线所成角
课堂探究
追问1:向量与的夹角与直线AM和CN夹角的联系?
答案: ,又两直线的夹角为锐角,所以
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
直线与直线所成角
课堂探究
追问2:如何表示向量与使我们方便计算它们的夹角?
方法2 建立空间直角坐标系
方法1 选择空间的一个基底
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
直线与直线所成角
课堂探究
例2:如图,在棱长为1的正四面体ABCD中,M,N分别为BC、AD的中点,求直线AM和CN夹角的余弦值.
直线与直线所成角
追问3:你能否通过向量运算,求出向量与夹角的余弦值,进而求出直线AM和CN夹角的余弦值.
课堂探究
追问4:你能归纳出利用向量求空间直线与直线所成角的一般方法吗?
课堂探究
化为向量问题
进行向量运算
回到图形问题
课堂探究
直线与平面所成角
问题2:斜线与平面所成的角的定义是什么?
答案:平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角;一条直线垂直于平面,它们所成的角是90o;一条直线和平面平行,或在平面内,它们所成的角是0o.直线与平面所成角的范围:
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
课堂探究
直线与平面所成角
追问:你能根据定义做出线面角吗?
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
答案:过直线上一点A,做平面α的垂线交平面α于点C,联接BC,∠ABC即为直线AB与平面α所成的角.
课堂探究
直线与平面所成角
问题3:这个问题的已知条件是什么?如何将几何问题
转化为向量问题?
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
答案:已知一条直线和一个平面,我们用一个点和方向向量表示直线,用一个点和法向量表示平面.因此,我们借助直线AB的方向向量u与平面α的法向量n的夹角
课堂探究
直线与平面所成角
追问:如何借助直线的方向向量u与平面的法向量n求直线和平面的夹角?
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
课堂探究
直线与平面所成角
小结:
已知直线AB与平面α相交与点B,求直线AB与平面α所成的角.
课堂探究
两相交平面所成角
问题4:类比已有的直线、平面所成角的定义,你认为合理定义两个平面所成的角?
答案:平面与平面相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面与平面的夹角.
追问1:你能说说平面与平面的夹角与二面角的区别与联系吗?
答案:二面角的大小是指其两个半平面的张开程度,可以用其平面角的大小来定义,它的取值范围是 ;而平面与平面的夹角是指平面与平面相交,形成的四个二面角中不大于90o的二面角,它的取值范围是 .
课堂探究
两相交平面所成角
追问2:角度是度量方向差异的量,那么决定平面方向的是什么?
答案:在空间向量里,通过一个点和法向量可以确定唯一的平面.
问题4:类比已有的直线、平面所成角的定义,你认为合理定义两个平面所成的角?
追问1:你能说说平面与平面的夹角与二面角的区别与联系吗?
课堂探究
两相交平面所成角
问题5:两个平面的法向量夹角与两个面夹角的关系?
答案:若平面与平面的法向量为n1,n2,则平面与平面的夹角即为向量为n1,n2的夹角或其补角.
课堂探究
两相交平面所成角
追问:为何向量夹角余弦值的绝对值为两个平面夹角的余弦值?
问题6:如何借助平面与平面的法向量为n1,n2求两个平面的夹角?
答案:
知识应用
例题讲解
例3: 如图,直棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1. 求平面PQR与平面A1B1C1夹角的余弦值.
分析:平面PQR与平面A1B1C1夹角可以转化为平面PQR与平面A1B1C1法向量的夹角,所以只需建立恰当的直角坐标系求出两个平面的法向量的夹角即可.
知识应用
例题讲解
解:
(化为向量问题)
以C1为坐标原点,C1A1,C1B1,C1C所在直线为x轴、y轴、z轴建立空间直角坐标系,设平面A1B1C1法向量为n1,平面PQR法向量为n2,平面PQR与平面A1B1C1夹角即为n1,n2的夹角或其补角.
例3: 如图,直棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1. 求平面PQR与平面A1B1C1夹角的余弦值.
知识应用
例题讲解
知识应用
例题讲解
归纳小结
本节课学习了什么内容?
异面直线夹角、线面角、两平面夹角的向量表示;
用向量方法解决立体几何问题的一般步骤.
再 见
