2014-2015学年广东省潮州市高二(下)期末数学试卷(文科) (解析版)
文档属性
| 名称 | 2014-2015学年广东省潮州市高二(下)期末数学试卷(文科) (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-27 13:02:10 | ||
图片预览




文档简介
2014-2015学年广东省潮州市高二(下)期末数学试卷(文科)
一、选择题(共10小题,每小题5分,满分50分)
1.(5分)(2015春?潮州期末)设全集U={1,3,5,6},集合M={1,a},?UM={5,6},则实数a的值为( )
A. 1 B. 3 C. 5 D. 6
考点: 补集及其运算.
专题: 集合.
分析: 由全集U及M的补集,确定出M,即可求出a的值.
解答: 解:∵全集U={1,3,5,6},集合M={1,a},?UM={5,6},
∴M={1,3},
则a=3,
故选:B.
点评: 此题考查了补集及其运算,熟练掌握补集的定义是解本题的关键.
2.(5分)(2015春?潮州期末)复数化简的结果为( )
A. ﹣1﹣i B. ﹣1+i C. 1﹣i D. 1+i
考点: 复数代数形式的乘除运算.
专题: 数系的扩充和复数.
分析: 利用复数的运算法则化简复数.
解答: 解:复数==1﹣i;
故选:C.
点评: 本题考查了复数的除法运算;将分母实数化是关键.
3.(5分)(2015春?潮州期末)化简:2log2510+log250.25=( )
A. 0 B. 1 C. 2 D. 4
考点: 对数的运算性质.
专题: 函数的性质及应用.
分析: 直接利用对数的运算法则化简求解即可.
解答: 解:2log2510+log250.25=log510+log50.5=log55=1.
故选:B.
点评: 本题考查导数的运算法则的应用,考查计算能力.
4.(5分)(2015春?潮州期末)类比“等差数列的定义”给出一个新数列“等和数列的定义”是( )
A. 连续两项的和相等的数列叫等和数列
B. 从第一项起,以后每一项与前一项的和都相等的数列叫等和数列
C. 从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列
D. 从第二项起,以后每一项与前一项的和都相等的数列叫等和数列
考点: 类比推理.
专题: 新定义.
分析: 由等差数列的定义,抓住其要点:①从第二项起,②每一项与前一项的差为定值,类比将差变为和后,即可得到等和数列的定义.
解答: 解:由等差数列的定义:从第二项起,以后每一项与前一项的差都相等的数列叫等差数列
类比可得:从第二项起,以后每一项与前一项的和都相等的数列叫等和数列
故选D
点评: 本题以类比推理为载体考查了等差数列的概念,熟练掌握等差数列的定义要点,及类比推理的实质是解答的关键.
5.(5分)(2015春?潮州期末)函数f(x)=﹣x的图象关于( )对称.
A. y轴 B. x轴 C. 坐标原点 D. 直线y=x
考点: 函数的图象.
专题: 函数的性质及应用.
分析: 先求出函数为奇函数,再根据奇函数的性质即可得到答案
解答: 解:因为f(x)=﹣x的定义域为(﹣∞,0)∪(0,+∞),
且f(﹣x)=﹣+x=﹣f(x),
所以f(x)为奇函数,
所以函数f(x)的图象关于坐标原点对称,
故选:C
点评: 本题考查了奇函数的性质,属于基础题
6.(5分)(2010?北京模拟)设f(x)=lgx+x﹣3,用二分法求方程lgx+x﹣3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
A. (2,2.25) B. (2.25,2.5) C. (2.5,2.75) D. (2.75,3)
考点: 二分法求方程的近似解.
专题: 计算题.
分析: 由已知“方程lgx+x﹣3=0在x∈(2,3)内近似解”,且具体的函数值的符号也已确定,由f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,即可求得结果.
解答: 解析:∵f(2.5)?f(2.75)<0,
由零点存在定理,得,
∴方程的根落在区间(2.5,2.75).
故选C.
点评: 二分法是求方程根的一种算法,其理论依据是零点存在定理:
一般地,若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,
且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点.
7.(5分)(2015春?潮州期末)已知函数f(x)=则f(5)等于( )
A. 2 B. 3 C. 4 D. ﹣2
考点: 函数的值.
专题: 函数的性质及应用.
分析: 首先由5<6得到f(5)=f(7),再由7>6,得到f(7)=75﹣,得到答案.
解答: 解:由已知函数f(x)=则f(5)=f(5+2)=f(7)=7﹣5=2.
故选:A.
点评: 本题考查了分段函数的函数值求法;关键是明确自变量范围,对号入座,代入对应的解析式求值.
8.(5分)(2015春?潮州期末)当a>1时,函数y=a﹣x与y=logax的图象是( )
A. B. C. D.
考点: 指数函数的图像与性质;对数函数的图像与性质.
专题: 函数的性质及应用.
分析: 由已知的a>1,得到<1,根据指数函数和对数函数的图象选择.
解答: 解:由a>1知,函数y=a﹣x=w为减函数,y=logax为增函数.
故选A.
点评: 本题考查了指数函数和对数函数的图象;关键是熟记指数函数和对数函数的图象和形状,明确底数与1的关系.
9.(5分)若函数f(x)是定义在R上的偶函数,在(﹣∞,0]上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是( )
A. (﹣∞,2) B. (2,+∞) C. (﹣∞,﹣2)∪(2,+∞) D. (﹣2,2)
考点: 偶函数.
专题: 压轴题.
分析: 偶函数图象关于y轴对称,所以只需求出(﹣∞,0]内的范围,再根据对称性写出解集.
解答: 解:当x∈(﹣∞,0]时f(x)<0则x∈(﹣2,0].
又∵偶函数关于y轴对称.
∴f(x)<0的解集为(﹣2,2),
故选D.
点评: 本题考查了偶函数的图象特征.在解决函数性质问题时要善于使用数形结合的思想.
10.(5分)(2015春?潮州期末)如图1是一个边长为1的正三角形,分别连接这个三角形三边中点,将在三角剖分成4个三角开(如图2),再分别连接图2中一个小三角形三边的中点,又可将原三角形剖分成7个三角形(如图3),…,依此类推,设第n个图中原三角形被剖分成an个三角形,则第4个图中最小三角形的边长为( );a100=( )
A. ,300 B. ,300 C. ,298 D. ,298
考点: 归纳推理.
专题: 推理和证明.
分析: 根据图形依次求出三角形个数和最小三角形的边长,根据等差、等比数列的特点进行归纳,再利用等差、等比数列的通项公式进行求解.
解答: 解:由题意得,图(1)、图(2)、图(3)中三角形被分割成1个,4个,7个;
∴三角形个数依次成等差数列,首项为1,公差为3,
∵图(1)、图(2)、图(3)中最小三角形的边长是1、、;
∴最小三角形的边长依次成等比数列,首项为1,公比为,
∴第4个图中最小三角形的边长为1×=,
a100=1+(100﹣1)×3=298,
故选:D.
点评: 本题考查了归纳推理,等差、等比数列的通项公式,考查图形变化的一般规律问题,通过观察掌握其内在规律,考查学生观察、分析、归纳能力,属基础题.
二、填空题(共4小题,每小题5分,满分20分)
11.(5分)(2015春?潮州期末)比较两个数的大小,则 < (填>,<或=).
考点: 指数函数单调性的应用.
专题: 函数的性质及应用.
分析: 利用指数函数的单调性进行判断.
解答: 解:因为,
设函数,则函数为单调递增函数,所以f(2.6)>f(1.8),
即<,
故答案为:<.
点评: 本题主要考查了指数幂的化简以及指数函数的单调性的应用,构造指数函数是解决本题的关键.
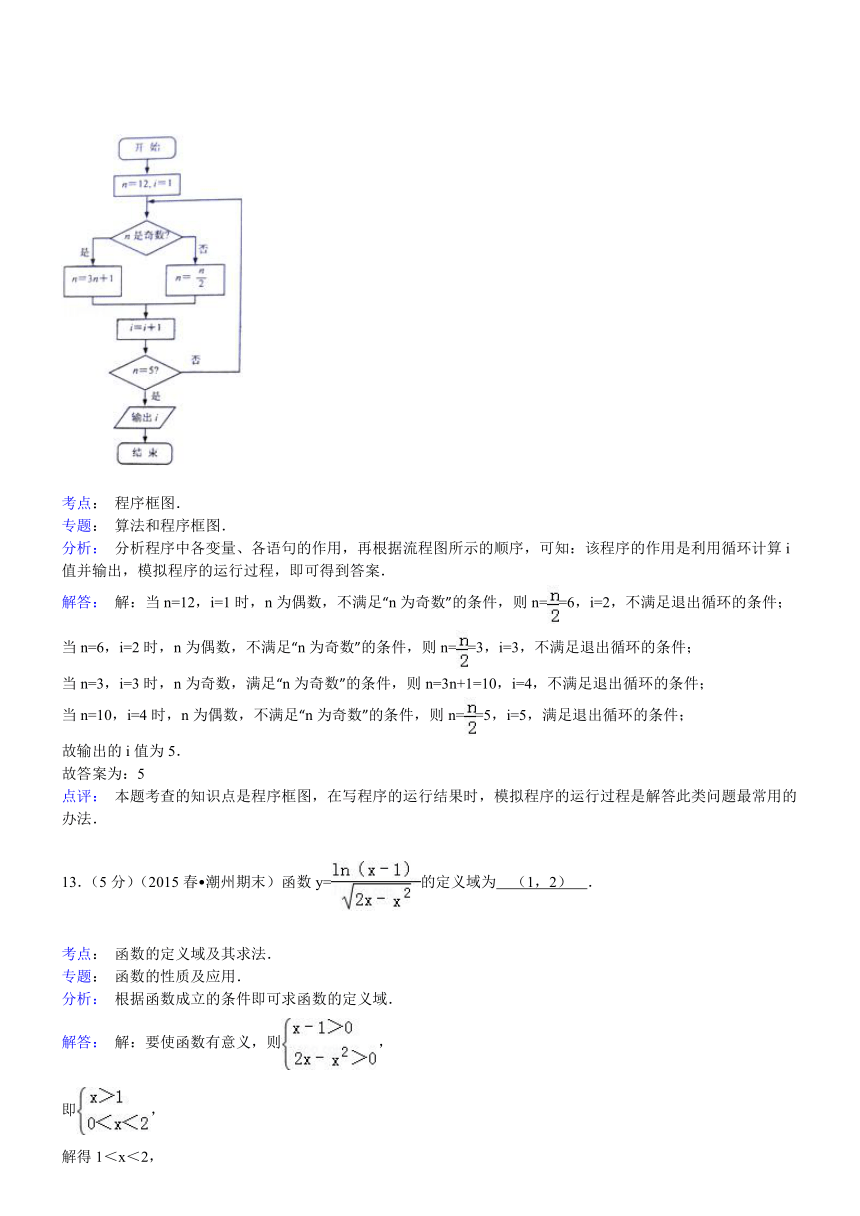
12.(5分)(2015春?潮州期末)若某程序框图如图所示,则该程序运行后输出的值是 5 .
考点: 程序框图.
专题: 算法和程序框图.
分析: 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算i值并输出,模拟程序的运行过程,即可得到答案.
解答: 解:当n=12,i=1时,n为偶数,不满足“n为奇数”的条件,则n==6,i=2,不满足退出循环的条件;
当n=6,i=2时,n为偶数,不满足“n为奇数”的条件,则n==3,i=3,不满足退出循环的条件;
当n=3,i=3时,n为奇数,满足“n为奇数”的条件,则n=3n+1=10,i=4,不满足退出循环的条件;
当n=10,i=4时,n为偶数,不满足“n为奇数”的条件,则n==5,i=5,满足退出循环的条件;
故输出的i值为5.
故答案为:5
点评: 本题考查的知识点是程序框图,在写程序的运行结果时,模拟程序的运行过程是解答此类问题最常用的办法.
13.(5分)(2015春?潮州期末)函数y=的定义域为 (1,2) .
考点: 函数的定义域及其求法.
专题: 函数的性质及应用.
分析: 根据函数成立的条件即可求函数的定义域.
解答: 解:要使函数有意义,则,
即,
解得1<x<2,
即函数的定义域为(1,2),
故答案为:(1,2)
点评: 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.
14.(5分)(2014?漳州校级模拟)函数f(x)的定义域为A,若x1,x2∈A且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数.例如,函数f(x)=2x+1(x∈R)是单函数.下列命题:
①函数f(x)=x2(x∈R)是单函数;
②若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
③若f:A→B为单函数,则对于任意b∈B,它至多有一个原象;
④函数f(x)在某区间上具有单调性,则f(x)一定是单函数.
其中的真命题是 ②③ .(写出所有真命题的编号)
考点: 抽象函数及其应用.
专题: 压轴题;新定义.
分析: 根据单函数的定义f(x1)=f(x2)时总有x1=x2,可知函数f(x)则对于任意b∈B,它至多有一个原象,而①④f(﹣1)=f(1),显然﹣1≠1,可知它不是单函数,②③都是,可得结果.
解答: 解:∵若x1,x2∈A,且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数
∴①函数f(x)=x2不是单函数,
∵f(﹣1)=f(1),显然﹣1≠1,
∴函数f(x)=x2(x∈R)不是单函数;
②∵函数f(x)=2x(x∈R)是增函数,
∴f(x1)=f(x2)时总有x1=x2,
即②正确;
③∵f(x)为单函数,对于任意b∈B,
若?x1≠x2,使得f(x1)=f(x2)=b,
则x1=x2,与x1≠x2矛盾
∴③正确;
④例如①函数f(x)=x2在(0,+∞)上是增函数,而它不是单函数;故④不正确.
故答案为:②③.
点评: 此题是个基础题.考查学生分析解决问题的能力,以及知识方法的迁移能力.
三、解答题(共6小题,满分80分)
15.(12分)(2015春?潮州期末)已知复数z1满足(z1﹣2)i=1+i,
(1)求z1;
(2)若复数z2的虚部为2,且z1?z2是实数,求复数z2.
考点: 复数代数形式的乘除运算;复数的基本概念.
专题: 计算题.
分析: (1)复数方程两边同乘复数i,然后化简即可求z1;
(2)复数z2的虚部为2,设出复数z2利用z1?z2是实数,复数的实部为0,即可求复数z2.
解答: 解:(1)复数z1满足(z1﹣2)i=1+i,所以z1﹣2=﹣i(1+i)=1﹣i
∴Z1=3﹣i…(6分)
(2)设z2=a+2i,所以z1?z2=(3﹣i)(a+2i)=3a+2+(6﹣a)i,
它是实数,所以a=6;
所以Z2=6+2i…(12分)
点评: 本题是基础题,考查复数的基本概念,复数的基本运算,考查计算能力,高考常考题型.
16.(12分)(2015春?潮州期末)若函数f(x)=在区间(﹣2,+∞)递增,求实数a的取值范围.
考点: 函数单调性的性质.
专题: 函数的性质及应用.
分析: 利用定义法结合分式函数的性质进行求解即可.
解答: 解:任取x1,x2∈(﹣2,+∞),且x1<x2,…(2分)
则f(x1)﹣f(x2)=﹣=.…(5分)
∵函数f(x)=在区间(﹣2,+∞)上为增函数,
∴f(x1)﹣f(x2)<0.…(7分)
∵x2﹣x1>0,x1+2>0,x2+2>0,
∴1﹣2a<0,故a>.…(10分)
即实数a的取值范围是(,+∞).…(12分)
点评: 本题主要考查函数单调性的应用,利用分式函数的性质以及函数单调性的定义是解决本题的关键.
17.(14分)(2012?福建)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元)
8
8.2
8.4
8.6
8.8
9
销量y(件)
90
84
83
80
75
68
(Ⅰ)求回归直线方程=bx+a,其中b=﹣20,a=﹣b;
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本)
考点: 回归分析的初步应用;线性回归方程.
专题: 计算题.
分析: (I)计算平均数,利用b=﹣20,a=﹣b,即可求得回归直线方程;
(II)设工厂获得的利润为L元,利用利润=销售收入﹣成本,建立函数,利用配方法可求工厂获得的利润最大.
解答: 解:(I),=
∵b=﹣20,a=﹣b,
∴a=80+20×8.5=250
∴回归直线方程=﹣20x+250;
(II)设工厂获得的利润为L元,则L=x(﹣20x+250)﹣4(﹣20x+250)=﹣20
∴该产品的单价应定为元,工厂获得的利润最大.
点评: 本题主要考查回归分析,考查二次函数,考查运算能力、应用意识,属于中档题.
18.(14分)(2015春?潮州期末)在数列{an}中,a1=2,an+1=,n=1,2,3,….
(1)计算a2,a3,a4的值,根据计算结果,猜想{an}通项公式;
(2)记bn=anan+1,其中,an是(1)的中猜想的结论,求证:b1+b2+…+bn<1.
考点: 数列递推式;归纳推理.
专题: 点列、递归数列与数学归纳法.
分析: (1)通过a1=2、an+1=,直接代入计算即可;
(2)通过,分离分母可得bn=﹣,并项相加计算即可.
解答: (1)解:∵a1=2,an+1=,
∴a2===,
a3===,
a4===,
猜想:;
(2)证明:∵,
∴
=,
∴=,
∵n∈N*,∴,即,
∴b1+b2+…+bn<1.
点评: 本题是一道关于数列的综合题,考查求数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.
19.(14分)(2015春?潮州期末)某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
25
学习积极性一般
25
合计
24
26
50
其中:“积极参加班级工作且学习积极性高的学生”的频率为0.36.
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=,(其中n=a+b+c+d)
临界值表:
P(K2≥K0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K0
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
考点: 独立性检验的应用.
专题: 计算题;概率与统计.
分析: (1)利用积极参加班级工作且学习积极性高的学生的频率为0.36,补全表中数据,根据古典概型的概率公式计算概率即可;
(2)计算观测值x2的值,对照表中数据得出统计结论.
解答: 解:(1)
积极参加班级工作 不太主动参加班级工作 合计
学习积极性高 18 7 25
学习积极性一般 6 19 25
合计 24 26 50
不太主动参加班级工作的学生有26人,总人数为50人.频率为.…(6分)
(2)假设学习积极性与对待班级工作的态度无关,由表中数据可得…(12分)
∴能在犯错误概率不超过0.001的前提下认为学习积极性与对待班级工作的态度有关系. …(14分)
点评: 本题考查了古典概型的应用问题,也考查了两个变量线性相关的应用问题,是基础题目.
20.(14分)(2015春?潮州期末)已知y=f(x)是定义在R上的奇函数,当x≤0时,f(x)=x﹣x2.
(1)求x>0时,f(x)的解析式;
(2)问是否存在这样的正实数a,b,当x∈[a,b]时,f(x)的值域为[4a﹣2,6b﹣6]?若存在,求出所有的a,b值;若不存在,请说明理由.
考点: 函数奇偶性的性质;函数的值域.
专题: 函数的性质及应用.
分析: (1)根据f(x)为奇函数,可设x>0,从而﹣x<0,从而f(﹣x)=﹣x﹣x2=﹣f(x),解出f(x)即可得出x>0时的f(x)的解析式;
(2)由上面x>0时,f(x)=x2+x,从而可判断此时f(x)在(0,+∞)上单调递增,从而可根据题意有,这样解出a,b,并满足a<b,即可找出所有的a,b值.
解答: 解:(1)设x>0,则﹣x<0,于是f(﹣x)=﹣x﹣x2;
又f(x)为奇函数,即f(﹣x)=﹣f(x);
即x>0时,f(x)=x+x2;
(2)假设存在这样的数a,b;
∵a>0,且f(x)=x+x2在x>0时为增函数;
∴x∈[a,b]时,f(x)∈[f(a),f(b)]=[4a﹣2,6b﹣6];
∴;
解得;
即,或,或,或;
∵a<b;
∴a,b的取值为,或,或.
点评: 考查奇函数的定义,二次函数的单调性,以及增函数在闭区间上的值域求法,注意条件a<b.
