湖南省株洲市重点中学2021-2022学年高三上学期期中测试数学试卷(含答案)
文档属性
| 名称 | 湖南省株洲市重点中学2021-2022学年高三上学期期中测试数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 694.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-05 18:27:38 | ||
图片预览


文档简介
2021-2022学年上学期高三数学期中测试卷
注意事项:
1.答卷前,考生务必将自己的姓名、 准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试题卷和答题卡一并交回。
一、单选题(本大题共8小题,每题5分,共40分,每小题只有一个选项符合题意)
1.设全集,集合 ,,则( )
A. B.
C. D.
2.已知复数,则( )
A.z的虚部为1 B.
C.为纯虚数 D.在复平面内对应的点位于第二象限
3.设表示直线,表示平面,若,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知平面向量、满足,若,则与的夹角为( )
A. B. C. D.
5.设,则,,则,,的大小关系是( ).
A. B. C. D.
6.中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“乐”不排在第一节,“射”和“御”两门课程不相邻,则“六艺”课程讲座不同的排课顺序共有( )种.
A.408 B.120 C.156 D.240
7.的内角、、的对边分别为、、,已知,该三角形的面积为,则的值为( )
A. B. C. D.
8.若关于x的不等式在上恒成立,则实数a的取值范围是( )
A. B.
C. D.
二、多选题(本大题共 4 小题,每题5分,共 20 分,每小题有多个选项符合题意,全部选对得 5分,部分选对的得2分,有选错的得0分)
9.设等差数列的前n项和为,且,,则下列结论正确的是( )
A. B.
C.数列是等差数列 D.对任意,都有
10.已知函数的部分图象如图所示,则下列说法正确的是( )
A. B.的最小正周期为
C.的图象关于直线对称 D.的图象关于点对称
11.已知圆,点为圆上一动点,为坐标原点,则下列说法中正确的是( )
A.的最大值为
B.的最小值为
C.直线的斜率范围为
D.以线段为直径的圆与圆的公共弦方程为
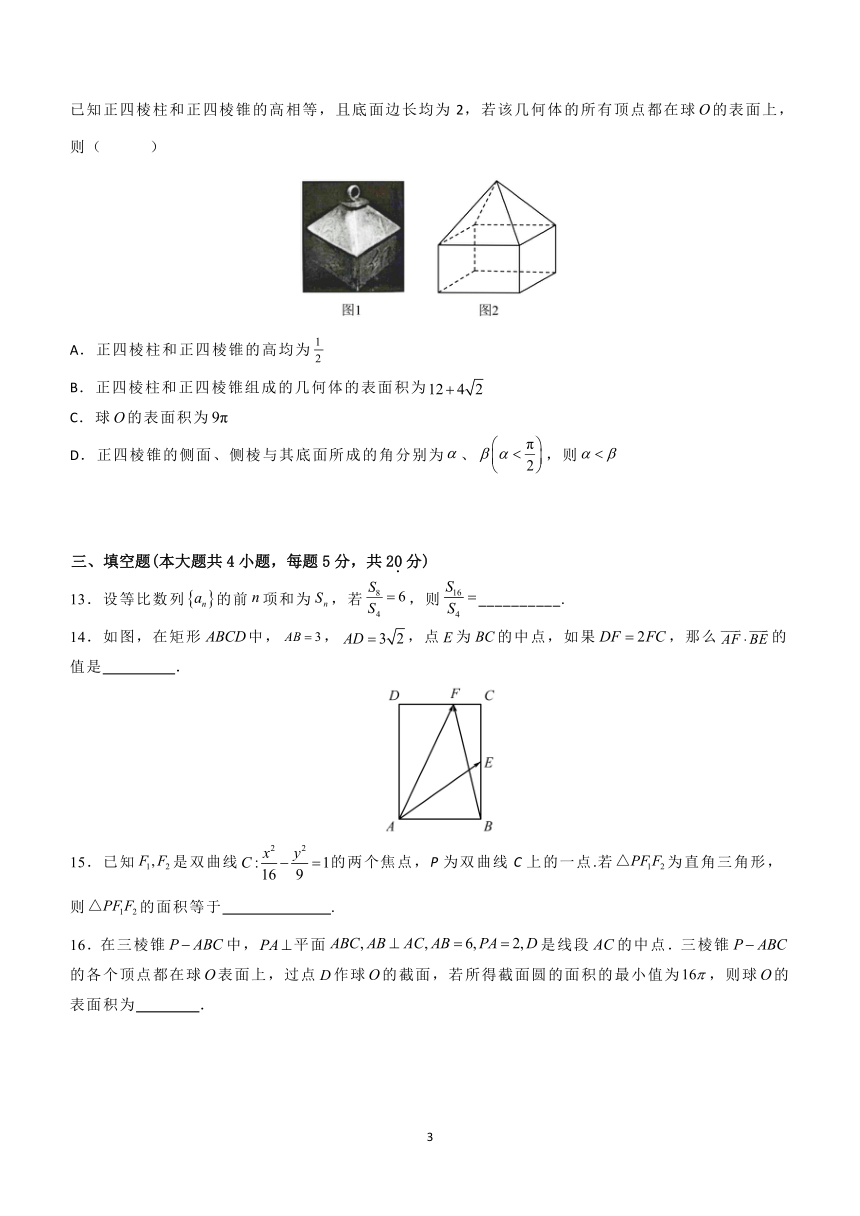
12.我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,本是官员或私人签署文件时代表身份的信物,后因其独特的文化内涵,也被作为装饰物来使用.图1是明清时期的一个金属印章摆件,除去顶部的环可以看作是一个正四棱柱和一个正四棱锥组成的几何体;如图2,已知正四棱柱和正四棱锥的高相等,且底面边长均为2,若该几何体的所有顶点都在球的表面上,则( )
A.正四棱柱和正四棱锥的高均为
B.正四棱柱和正四棱锥组成的几何体的表面积为
C.球的表面积为
D.正四棱锥的侧面、侧棱与其底面所成的角分别为、,则
三、填空题(本大题共4小题,每题5分,共20分)
13.设等比数列的前项和为,若,则__________.
14.如图,在矩形中,,,点为的中点,如果,那么的值是 .
15.已知是双曲线的两个焦点,P为双曲线C上的一点.若为直角三角形,则的面积等于 .
16.在三棱锥中,平面是线段的中点.三棱锥的各个顶点都在球表面上,过点作球的截面,若所得截面圆的面积的最小值为,则球的表面积为 .
四、解答题(本大题共6 小题,共 70分,17题为10分,18-22每题12分,解答应写出文字说明,证明过程或演算步骤)
17.中,,,.
(1)求;
(2)平面四边形中,,,求的面积.
18.公比为的等比数列的前项和.
(1)求与的值;
(2)若,记数列的前项和为,求证:.
19.经观测,某昆虫的产卵数与温度有关,现将收集到的温度和产卵数的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
275 731.1 21.7 150 2368.36 30
表中,
(1)根据散点图判断,,与哪一个适宜作为 与之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求关于回归方程;
②已知用人工培养该昆虫的成本与温度和产卵数的关系为,当温度 (取整数)为何值时,培养成本的预报值最小?
附:对于一组数据,, ,其回归直线的斜率和截距的最小二乘估计分别为, .
20.如图,圆台 的轴截面为等腰梯形 为底面圆周上异于的点,
(1)若是线段的中点,求证:平面;
(2)若,设直线为平面与平面的交线,点 与平面 所成角为,求的最大值.
21.已知椭圆:的离心率为.点在椭圆上,点,,的面积为,为坐标原点.
(1)求椭圆的标准方程;
(2)若直线交椭圆于,两点,直线的斜率为,直线的斜率为,且,证明:的面积是定值,并求此定值.
22.已知函数.
(1)若函数在区间内有两个极值点,,求实数的取值范围;
(2)在(1)的基础上,求证:.
参考答案
单选题 DCDABAAA
多选题 BCD BCD AC BC
13.156
14.9
15.或9
16.
17.(1)
(2)
18.(1),
(2)证明略
19.(1)更适宜;(2)①;②14.
20.
(1)证明略
(2)
21.(1);(2)定值为
22.(1) (2)证明略
注意事项:
1.答卷前,考生务必将自己的姓名、 准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试题卷和答题卡一并交回。
一、单选题(本大题共8小题,每题5分,共40分,每小题只有一个选项符合题意)
1.设全集,集合 ,,则( )
A. B.
C. D.
2.已知复数,则( )
A.z的虚部为1 B.
C.为纯虚数 D.在复平面内对应的点位于第二象限
3.设表示直线,表示平面,若,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知平面向量、满足,若,则与的夹角为( )
A. B. C. D.
5.设,则,,则,,的大小关系是( ).
A. B. C. D.
6.中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“乐”不排在第一节,“射”和“御”两门课程不相邻,则“六艺”课程讲座不同的排课顺序共有( )种.
A.408 B.120 C.156 D.240
7.的内角、、的对边分别为、、,已知,该三角形的面积为,则的值为( )
A. B. C. D.
8.若关于x的不等式在上恒成立,则实数a的取值范围是( )
A. B.
C. D.
二、多选题(本大题共 4 小题,每题5分,共 20 分,每小题有多个选项符合题意,全部选对得 5分,部分选对的得2分,有选错的得0分)
9.设等差数列的前n项和为,且,,则下列结论正确的是( )
A. B.
C.数列是等差数列 D.对任意,都有
10.已知函数的部分图象如图所示,则下列说法正确的是( )
A. B.的最小正周期为
C.的图象关于直线对称 D.的图象关于点对称
11.已知圆,点为圆上一动点,为坐标原点,则下列说法中正确的是( )
A.的最大值为
B.的最小值为
C.直线的斜率范围为
D.以线段为直径的圆与圆的公共弦方程为
12.我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,本是官员或私人签署文件时代表身份的信物,后因其独特的文化内涵,也被作为装饰物来使用.图1是明清时期的一个金属印章摆件,除去顶部的环可以看作是一个正四棱柱和一个正四棱锥组成的几何体;如图2,已知正四棱柱和正四棱锥的高相等,且底面边长均为2,若该几何体的所有顶点都在球的表面上,则( )
A.正四棱柱和正四棱锥的高均为
B.正四棱柱和正四棱锥组成的几何体的表面积为
C.球的表面积为
D.正四棱锥的侧面、侧棱与其底面所成的角分别为、,则
三、填空题(本大题共4小题,每题5分,共20分)
13.设等比数列的前项和为,若,则__________.
14.如图,在矩形中,,,点为的中点,如果,那么的值是 .
15.已知是双曲线的两个焦点,P为双曲线C上的一点.若为直角三角形,则的面积等于 .
16.在三棱锥中,平面是线段的中点.三棱锥的各个顶点都在球表面上,过点作球的截面,若所得截面圆的面积的最小值为,则球的表面积为 .
四、解答题(本大题共6 小题,共 70分,17题为10分,18-22每题12分,解答应写出文字说明,证明过程或演算步骤)
17.中,,,.
(1)求;
(2)平面四边形中,,,求的面积.
18.公比为的等比数列的前项和.
(1)求与的值;
(2)若,记数列的前项和为,求证:.
19.经观测,某昆虫的产卵数与温度有关,现将收集到的温度和产卵数的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
275 731.1 21.7 150 2368.36 30
表中,
(1)根据散点图判断,,与哪一个适宜作为 与之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求关于回归方程;
②已知用人工培养该昆虫的成本与温度和产卵数的关系为,当温度 (取整数)为何值时,培养成本的预报值最小?
附:对于一组数据,, ,其回归直线的斜率和截距的最小二乘估计分别为, .
20.如图,圆台 的轴截面为等腰梯形 为底面圆周上异于的点,
(1)若是线段的中点,求证:平面;
(2)若,设直线为平面与平面的交线,点 与平面 所成角为,求的最大值.
21.已知椭圆:的离心率为.点在椭圆上,点,,的面积为,为坐标原点.
(1)求椭圆的标准方程;
(2)若直线交椭圆于,两点,直线的斜率为,直线的斜率为,且,证明:的面积是定值,并求此定值.
22.已知函数.
(1)若函数在区间内有两个极值点,,求实数的取值范围;
(2)在(1)的基础上,求证:.
参考答案
单选题 DCDABAAA
多选题 BCD BCD AC BC
13.156
14.9
15.或9
16.
17.(1)
(2)
18.(1),
(2)证明略
19.(1)更适宜;(2)①;②14.
20.
(1)证明略
(2)
21.(1);(2)定值为
22.(1) (2)证明略
同课章节目录
