同步课时精练(七)2.3单摆(后附解析)
文档属性
| 名称 | 同步课时精练(七)2.3单摆(后附解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-05 00:00:00 | ||
图片预览




文档简介
同步课时精练(七)2.3 单摆(后附解析)
一、单选题
1.下列情况下,会使单摆周期变大的是( )
A.减少单摆摆球的质量
B.增大单摆摆球的质量
C.将摆从赤道移到北极
D.将摆从地球移到月球上
2.做简谐运动的单摆,其摆长不变,若摆球的质量增加为原来的倍,摆球经过平衡位置的速度减为原来的,则单摆振动的( )
A.周期不变,振幅不变 B.周期不变,振幅变小
C.周期改变,振幅不变 D.周期改变,振幅变大
3.单摆运动具有周期性,关于单摆周期,下列说法中正确的是( )
A.单摆的质量越大,回复力越大,周期越短
B.单摆周期与单摆所处的地理位置有关,与摆长无关
C.不同单摆放在同一地方,摆长越长的单摆的周期越长
D.若用单摆制成的座钟在张家口走时准确,则搬到深圳后不作任何调整走时仍准确
4.如图所示,两块不带电的平行金属板之间用绝缘细绳悬挂一带负电的小球,把小球向左拉开一定角度(角度很小且小于)由静止释放,小球以一定的周期做往复运动。若将两极板通过导线、开关与图示电源相接,当闭合开关且板间电压稳定后(小球重力大于电场力),则( )
A.小球摆动的周期保持不变
B.小球摆动的周期变大
C.若把电源的正负极对调,小球摆动的周期保持不变
D.若把电源的正负极对调,小球摆动的周期变大
5.下列关于机械振动的说法错误的是( )
A.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,与系统的固有频率无关
B.弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变
C.在同一地点,单摆做简谐振动的周期的平方与其摆长成正比
D.已知弹簧振子初始时刻的位置、振幅及周期,就可以确定振子在任意时刻的振动情况
6.如图甲所示,挖掘机的顶部垂下一个大铁球并让它小幅度地摆动,即可用来拆卸混凝土建筑,可视为单摆模型,它对应的振动图像如图乙所示,则下列说法正确的是( )
A.单摆振动的周期是4s
B.t=2s时,摆球的速度最大
C.摆球的质量增大,周期变小
D.该单摆的摆长约为8m
7.如图甲所示,一单摆做小角度摆动,从某次摆球由左向右通过平衡位置开始计时,相对平衡位置的位移x随时间t变化的图像如图乙所示。不计空气阻力,重力加速度g取10m/s2.对于这个单摆的振动过程,下列说法正确的是( )
A.单摆的摆长约为2.0m
B.单摆的位移x随时间t变化的关系式为x=8sinπt(cm)
C.从t=0.5s到t=1.0s的过程中,摆球的重力势能逐渐增大
D.从t=1.0s到t=1.5s的过程中,摆球所受回复力逐渐减小
8.将一个摆长为l的单摆放在一个光滑的,倾角为α的斜面上,其摆角为,如图下列说法正确的是( )
A.摆球做简谐运动的回复力
B.摆球做简谐运动的回复力为
C.摆球做简谐运动的周期为
D.摆球在运动过程中,经平衡位置时,线的拉力为
9.在上海走时准确的摆钟移到哈尔滨后,为使摆钟仍然准确走时,下列调解措施正确的是( )
A.将钟摆的质量减小 B.增大钟摆摆长
C.将钟摆的材质由钢铁改为黄铜 D.将钟摆振幅减半
二、多选题
10.小球在一个曲率半径很大的光滑圆槽内做简谐振动,如图所示,为了使振动周期变为原来的2倍,可采用的方法是( )
A.将小球质量减为原来的一半
B.将其振幅变为原来的2倍
C.将圆槽半径增为原来的4倍
D.将圆槽从地面移到距地面为1倍地球半径的高空
11.如图所示,一单摆在做简谐运动。下列可以增大单摆周期的操作是( )
A.减小单摆的振幅 B.增大摆球的质量
C.增加摆线的摆长 D.将单摆拿到山上
12.质量为m的带正电小球悬挂在绝缘细线上,小球视为质点,绝缘细线长为L,整个空间有水平方向场强为E的匀强电场,当小球静止时,细线与竖直方向成角(),重力加速度为g。若保持场强大小不变方向迅速改为竖直向下,小球从图示位置到第一次经过最低点需要时间为t,则( )
A.小球所带电荷量为
B.小球所带电荷量为
C.
D.
三、解答题
13.如图所示,MN为半径较大的光滑圆弧轨道的一部分,把小球A放在MN的圆心处,再把另一小球B放在MN上离最低点C很近的B处,今使两球同时自由释放,则在不计空气阻力时,通过计算说明哪个小球先到达C点?
14.如图,一个半径为R的凹槽,该槽是圆柱体侧表面的一部分。MN、PQ为圆柱表面的母线,MN=PQ=L,在其一端的最低处有一小孔B。一半径略小于B孔半径且远小于R的小球,位于槽的另一端边缘点A处(A靠近槽的最低点),不计摩擦。
(1)若小球初速度为零,求小球运动到轨道最低点的时间;
(2)若小球以初速度开始沿平行于MN的方向运动,要使小球运动到槽的另一端时,恰能落入B孔中,求小球的初速度和L应满足的关系式。
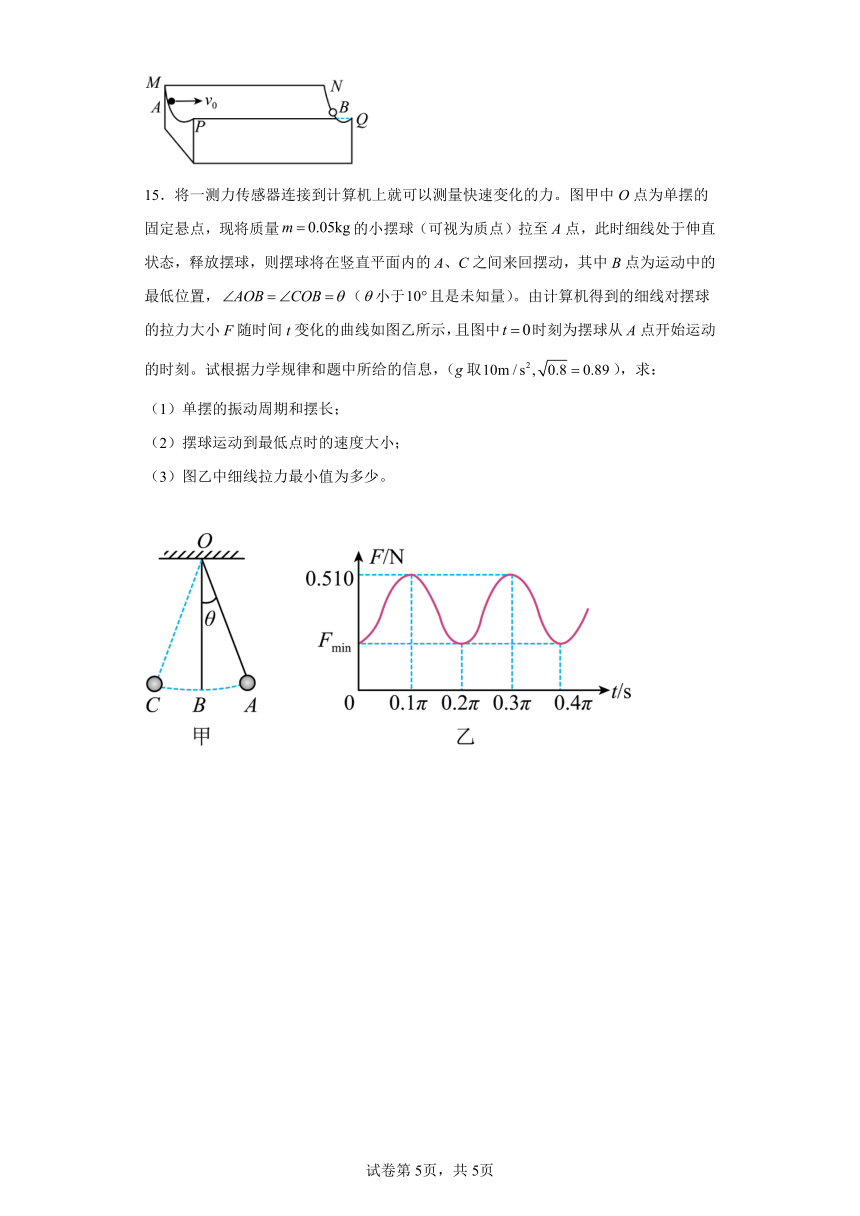
15.将一测力传感器连接到计算机上就可以测量快速变化的力。图甲中O点为单摆的固定悬点,现将质量的小摆球(可视为质点)拉至A点,此时细线处于伸直状态,释放摆球,则摆球将在竖直平面内的A、C之间来回摆动,其中B点为运动中的最低位置,(小于且是未知量)。由计算机得到的细线对摆球的拉力大小F随时间t变化的曲线如图乙所示,且图中时刻为摆球从A点开始运动的时刻。试根据力学规律和题中所给的信息,(g取),求:
(1)单摆的振动周期和摆长;
(2)摆球运动到最低点时的速度大小;
(3)图乙中细线拉力最小值为多少。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
解析:单摆周期计算公式为
则单摆质量不影响周期,想要使周期变大,可以增大摆长或者减小g,故可以将摆从地球移到月球上,这样重力加速度g减小了,从赤道移到北极会使g增大,这样就减小了周期,故只有D选项正确。
答案:D。
2.B
解析:由单摆的周期公式可知,单摆摆长不变,则周期不变;摆球经过平衡位置的速度减为原来的,由于振动过程中机械能守恒,则有
mgh=mv2
则有
2gh=v2
据此式可知,速度变小,高度减小,所以偏离平衡位置的最大距离变小,即振幅变小。
答案:B。
点拨:单摆的摆长和重力加速度的大小决定单摆的周期的大小,单摆的能量决定单摆的振幅的大小。
3.C
解析:ABC.根据单摆的周期
知小球的周期与质量、振幅(路程)都无关,与摆长以及重力加速度有关,故C正确,AB错误;
D.根据重力加速度的特点可以知道,张家口的重力加速度大于深圳的重力加速度,根
可以知道,单摆制成的座钟在张家口走时准确,在搬到深圳后周期增大,要走时仍然准确,必须调整缩短单摆的摆长,故D错误。
答案:C。
4.B
解析:AB.根据题意可知,当开关闭合时,平行金属板间存在竖直向下的电场,带负电的小球受竖直向上的电场力,则等效重力加速度减小,由单摆周期公式可知,小球摆动周期变大,故A错误,B正确;
CD.若把电源的正负极对调,当开关闭合时,平行金属板间存在竖直向上的电场,带负电的小球受竖直向下的电场力,则等效重力加速度增大,由单摆周期公式可知,小球摆动周期变小,故CD错误。
答案:B。
5.D
解析:A.根据受迫振动的特点可知,系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,与系统的固有频率无关,故A不符合题意;
B.弹簧振子做简谐振动时,只有重力或弹簧的弹力做功,振动系统的势能与动能之和保持不变,故B不符合题意;
C.根据单摆的周期公式
可知在同一地点,单摆做简谐振动的周期的平方与其摆长成正比,故C不符合题意;
D.已知弹簧振子初始时刻的位置及其振动周期,在不知道初始时刻的运动方向的情况下,弹簧振子的振动方程可能有两种不同的情况,所以不可判断出振子在任意时刻运动速度的方向,故D符合题意。
答案:D。
6.B
解析:A.由图乙可以看出单摆振动的周期为8s。故A错误;
B.由题知,t=2s时,摆球处于平衡位置,即单摆的最低点,故摆球的速度最大。故B正确;
C.根据单摆周期公式
易知单摆周期与摆球的质量无关。故C错误;
D.同理,由单摆周期公式
解得
故D错误。
答案:B。
7.B
解析:A.由题图乙可知,单摆的周期为T=2s,由单摆的周期公式
可得
A错误;
B.由图乙可知:振幅A=8cm,,角速度
单摆的位移x随时间t变化的关系式为x=8sinπt(cm)
B正确;
C.由图乙可知,从t=0.5s到t=1.0s的振动中,摆球从右侧最高点向平衡位置运动,摆球的速度逐渐增大,动能逐渐增大,重力势能逐渐减小,C错误;
D.由图乙可知,从t=1.0s到t=1.5s的的振动中,摆球从平衡位置向左运动到最大位移处,由简谐运动的受回复力特点F= kx可知,摆球所受回复力逐渐增大,D错误。
答案:B。
8.A
解析:本题是类似单摆模型,回复力是重力的下滑分力的切向分量提供,重力的下滑分力为mgsinα,下滑分力的切线分力为mgsinαsinθ,故A正确,B错误;类似单摆模型,等效重力加速度为gsinα,故周期为:,故C错误;摆球在运动过程中,经平衡位置时,线的拉力和重力的下滑分力的合力提供向心力,故,故T>mgsinα,故D错误.
9.B
解析:在上海走时准确的摆钟移到哈尔滨后,由于纬度变大,重力加速度g增大,根据单摆的周期公式
可知,其周期与钟摆的质量,材质,振幅无关,为使摆钟仍然准确走时,必须增大钟摆摆长,所以B正确;ACD错误;
答案:B。
10.CD
解析:小球受重力和支持力,支持力的切向分量提供向心力,是类似单摆模型,根据单摆的周期公式
周期与振幅、摆球的重力均无关,要使振动周期变为原来的2倍,可以将圆槽半径变为原来的4倍。或者将当地的重力加速度变为原来的四分之一。
将圆槽从地面移到距地面为1倍地球半径的高空,有
联立,可知
故AB错误;CD正确。
答案:CD。
11.CD
解析:由单摆周期公式得
要增大单摆的周期,可以增加摆线的摆长,或者减小,与单摆的振幅和摆球的质量无关,又因为海拔越高值越小,所以将单摆拿到山上可以增大单摆的周期。
答案:CD。
12.AC
解析:AB.整个空间有水平方向场强为E的匀强电场时,对小球由平衡条件可得
解得
故A正确,B错误;
CD.若保持场强大小不变方向迅速改为竖直向下时,等效重力加速度
结合单摆周期公式可得
则小球从图示位置到第一次经过最低点需要时间
故C正确,D错误。
答案:AC。
13.A球先到达C点
解析:A做自由落体运动,到达C所需时间为:,R为圆弧轨道的半径:因为圆弧轨道的半径很大球离最低点C又很近,所以B球在轨道给它的支持力和重力的作用下沿圆弧做简谐运动(等同于摆长为R的单摆),则运动到最低点C所用的时间是单摆振动周期的,即为:>,所以A球先到达C点.
14.(1)(n=0,1,2,3,…);(2)(n=0,1,2,3,…)
解析:(1)如果小球没有初速度则小球做简谐运动,简谐运动的周期为
小球运动到轨道最低点的时间
,(n=0,1,2,3,…)
(2)沿MN方向小球做匀速直线运动,则
L=v0t
解得
,(n=0,1,2,3,…)
15.(1)T=0.4πs;L=0.4m(2)0.089m/s;(3)0.495N
解析:(1)由F-t图可得
T=0.4πs
由
得
L=0.4m
(2)由F-t图可得,摆球运动到最低点时细线的拉力
Fmax=0.510N
此时有
Fmax-mg=m
解得
v=0.089m/s
(3)A→B机械能守恒
Fmin=mgcos
解得
Fmin=0.495N
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列情况下,会使单摆周期变大的是( )
A.减少单摆摆球的质量
B.增大单摆摆球的质量
C.将摆从赤道移到北极
D.将摆从地球移到月球上
2.做简谐运动的单摆,其摆长不变,若摆球的质量增加为原来的倍,摆球经过平衡位置的速度减为原来的,则单摆振动的( )
A.周期不变,振幅不变 B.周期不变,振幅变小
C.周期改变,振幅不变 D.周期改变,振幅变大
3.单摆运动具有周期性,关于单摆周期,下列说法中正确的是( )
A.单摆的质量越大,回复力越大,周期越短
B.单摆周期与单摆所处的地理位置有关,与摆长无关
C.不同单摆放在同一地方,摆长越长的单摆的周期越长
D.若用单摆制成的座钟在张家口走时准确,则搬到深圳后不作任何调整走时仍准确
4.如图所示,两块不带电的平行金属板之间用绝缘细绳悬挂一带负电的小球,把小球向左拉开一定角度(角度很小且小于)由静止释放,小球以一定的周期做往复运动。若将两极板通过导线、开关与图示电源相接,当闭合开关且板间电压稳定后(小球重力大于电场力),则( )
A.小球摆动的周期保持不变
B.小球摆动的周期变大
C.若把电源的正负极对调,小球摆动的周期保持不变
D.若把电源的正负极对调,小球摆动的周期变大
5.下列关于机械振动的说法错误的是( )
A.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,与系统的固有频率无关
B.弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变
C.在同一地点,单摆做简谐振动的周期的平方与其摆长成正比
D.已知弹簧振子初始时刻的位置、振幅及周期,就可以确定振子在任意时刻的振动情况
6.如图甲所示,挖掘机的顶部垂下一个大铁球并让它小幅度地摆动,即可用来拆卸混凝土建筑,可视为单摆模型,它对应的振动图像如图乙所示,则下列说法正确的是( )
A.单摆振动的周期是4s
B.t=2s时,摆球的速度最大
C.摆球的质量增大,周期变小
D.该单摆的摆长约为8m
7.如图甲所示,一单摆做小角度摆动,从某次摆球由左向右通过平衡位置开始计时,相对平衡位置的位移x随时间t变化的图像如图乙所示。不计空气阻力,重力加速度g取10m/s2.对于这个单摆的振动过程,下列说法正确的是( )
A.单摆的摆长约为2.0m
B.单摆的位移x随时间t变化的关系式为x=8sinπt(cm)
C.从t=0.5s到t=1.0s的过程中,摆球的重力势能逐渐增大
D.从t=1.0s到t=1.5s的过程中,摆球所受回复力逐渐减小
8.将一个摆长为l的单摆放在一个光滑的,倾角为α的斜面上,其摆角为,如图下列说法正确的是( )
A.摆球做简谐运动的回复力
B.摆球做简谐运动的回复力为
C.摆球做简谐运动的周期为
D.摆球在运动过程中,经平衡位置时,线的拉力为
9.在上海走时准确的摆钟移到哈尔滨后,为使摆钟仍然准确走时,下列调解措施正确的是( )
A.将钟摆的质量减小 B.增大钟摆摆长
C.将钟摆的材质由钢铁改为黄铜 D.将钟摆振幅减半
二、多选题
10.小球在一个曲率半径很大的光滑圆槽内做简谐振动,如图所示,为了使振动周期变为原来的2倍,可采用的方法是( )
A.将小球质量减为原来的一半
B.将其振幅变为原来的2倍
C.将圆槽半径增为原来的4倍
D.将圆槽从地面移到距地面为1倍地球半径的高空
11.如图所示,一单摆在做简谐运动。下列可以增大单摆周期的操作是( )
A.减小单摆的振幅 B.增大摆球的质量
C.增加摆线的摆长 D.将单摆拿到山上
12.质量为m的带正电小球悬挂在绝缘细线上,小球视为质点,绝缘细线长为L,整个空间有水平方向场强为E的匀强电场,当小球静止时,细线与竖直方向成角(),重力加速度为g。若保持场强大小不变方向迅速改为竖直向下,小球从图示位置到第一次经过最低点需要时间为t,则( )
A.小球所带电荷量为
B.小球所带电荷量为
C.
D.
三、解答题
13.如图所示,MN为半径较大的光滑圆弧轨道的一部分,把小球A放在MN的圆心处,再把另一小球B放在MN上离最低点C很近的B处,今使两球同时自由释放,则在不计空气阻力时,通过计算说明哪个小球先到达C点?
14.如图,一个半径为R的凹槽,该槽是圆柱体侧表面的一部分。MN、PQ为圆柱表面的母线,MN=PQ=L,在其一端的最低处有一小孔B。一半径略小于B孔半径且远小于R的小球,位于槽的另一端边缘点A处(A靠近槽的最低点),不计摩擦。
(1)若小球初速度为零,求小球运动到轨道最低点的时间;
(2)若小球以初速度开始沿平行于MN的方向运动,要使小球运动到槽的另一端时,恰能落入B孔中,求小球的初速度和L应满足的关系式。
15.将一测力传感器连接到计算机上就可以测量快速变化的力。图甲中O点为单摆的固定悬点,现将质量的小摆球(可视为质点)拉至A点,此时细线处于伸直状态,释放摆球,则摆球将在竖直平面内的A、C之间来回摆动,其中B点为运动中的最低位置,(小于且是未知量)。由计算机得到的细线对摆球的拉力大小F随时间t变化的曲线如图乙所示,且图中时刻为摆球从A点开始运动的时刻。试根据力学规律和题中所给的信息,(g取),求:
(1)单摆的振动周期和摆长;
(2)摆球运动到最低点时的速度大小;
(3)图乙中细线拉力最小值为多少。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
解析:单摆周期计算公式为
则单摆质量不影响周期,想要使周期变大,可以增大摆长或者减小g,故可以将摆从地球移到月球上,这样重力加速度g减小了,从赤道移到北极会使g增大,这样就减小了周期,故只有D选项正确。
答案:D。
2.B
解析:由单摆的周期公式可知,单摆摆长不变,则周期不变;摆球经过平衡位置的速度减为原来的,由于振动过程中机械能守恒,则有
mgh=mv2
则有
2gh=v2
据此式可知,速度变小,高度减小,所以偏离平衡位置的最大距离变小,即振幅变小。
答案:B。
点拨:单摆的摆长和重力加速度的大小决定单摆的周期的大小,单摆的能量决定单摆的振幅的大小。
3.C
解析:ABC.根据单摆的周期
知小球的周期与质量、振幅(路程)都无关,与摆长以及重力加速度有关,故C正确,AB错误;
D.根据重力加速度的特点可以知道,张家口的重力加速度大于深圳的重力加速度,根
可以知道,单摆制成的座钟在张家口走时准确,在搬到深圳后周期增大,要走时仍然准确,必须调整缩短单摆的摆长,故D错误。
答案:C。
4.B
解析:AB.根据题意可知,当开关闭合时,平行金属板间存在竖直向下的电场,带负电的小球受竖直向上的电场力,则等效重力加速度减小,由单摆周期公式可知,小球摆动周期变大,故A错误,B正确;
CD.若把电源的正负极对调,当开关闭合时,平行金属板间存在竖直向上的电场,带负电的小球受竖直向下的电场力,则等效重力加速度增大,由单摆周期公式可知,小球摆动周期变小,故CD错误。
答案:B。
5.D
解析:A.根据受迫振动的特点可知,系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,与系统的固有频率无关,故A不符合题意;
B.弹簧振子做简谐振动时,只有重力或弹簧的弹力做功,振动系统的势能与动能之和保持不变,故B不符合题意;
C.根据单摆的周期公式
可知在同一地点,单摆做简谐振动的周期的平方与其摆长成正比,故C不符合题意;
D.已知弹簧振子初始时刻的位置及其振动周期,在不知道初始时刻的运动方向的情况下,弹簧振子的振动方程可能有两种不同的情况,所以不可判断出振子在任意时刻运动速度的方向,故D符合题意。
答案:D。
6.B
解析:A.由图乙可以看出单摆振动的周期为8s。故A错误;
B.由题知,t=2s时,摆球处于平衡位置,即单摆的最低点,故摆球的速度最大。故B正确;
C.根据单摆周期公式
易知单摆周期与摆球的质量无关。故C错误;
D.同理,由单摆周期公式
解得
故D错误。
答案:B。
7.B
解析:A.由题图乙可知,单摆的周期为T=2s,由单摆的周期公式
可得
A错误;
B.由图乙可知:振幅A=8cm,,角速度
单摆的位移x随时间t变化的关系式为x=8sinπt(cm)
B正确;
C.由图乙可知,从t=0.5s到t=1.0s的振动中,摆球从右侧最高点向平衡位置运动,摆球的速度逐渐增大,动能逐渐增大,重力势能逐渐减小,C错误;
D.由图乙可知,从t=1.0s到t=1.5s的的振动中,摆球从平衡位置向左运动到最大位移处,由简谐运动的受回复力特点F= kx可知,摆球所受回复力逐渐增大,D错误。
答案:B。
8.A
解析:本题是类似单摆模型,回复力是重力的下滑分力的切向分量提供,重力的下滑分力为mgsinα,下滑分力的切线分力为mgsinαsinθ,故A正确,B错误;类似单摆模型,等效重力加速度为gsinα,故周期为:,故C错误;摆球在运动过程中,经平衡位置时,线的拉力和重力的下滑分力的合力提供向心力,故,故T>mgsinα,故D错误.
9.B
解析:在上海走时准确的摆钟移到哈尔滨后,由于纬度变大,重力加速度g增大,根据单摆的周期公式
可知,其周期与钟摆的质量,材质,振幅无关,为使摆钟仍然准确走时,必须增大钟摆摆长,所以B正确;ACD错误;
答案:B。
10.CD
解析:小球受重力和支持力,支持力的切向分量提供向心力,是类似单摆模型,根据单摆的周期公式
周期与振幅、摆球的重力均无关,要使振动周期变为原来的2倍,可以将圆槽半径变为原来的4倍。或者将当地的重力加速度变为原来的四分之一。
将圆槽从地面移到距地面为1倍地球半径的高空,有
联立,可知
故AB错误;CD正确。
答案:CD。
11.CD
解析:由单摆周期公式得
要增大单摆的周期,可以增加摆线的摆长,或者减小,与单摆的振幅和摆球的质量无关,又因为海拔越高值越小,所以将单摆拿到山上可以增大单摆的周期。
答案:CD。
12.AC
解析:AB.整个空间有水平方向场强为E的匀强电场时,对小球由平衡条件可得
解得
故A正确,B错误;
CD.若保持场强大小不变方向迅速改为竖直向下时,等效重力加速度
结合单摆周期公式可得
则小球从图示位置到第一次经过最低点需要时间
故C正确,D错误。
答案:AC。
13.A球先到达C点
解析:A做自由落体运动,到达C所需时间为:,R为圆弧轨道的半径:因为圆弧轨道的半径很大球离最低点C又很近,所以B球在轨道给它的支持力和重力的作用下沿圆弧做简谐运动(等同于摆长为R的单摆),则运动到最低点C所用的时间是单摆振动周期的,即为:>,所以A球先到达C点.
14.(1)(n=0,1,2,3,…);(2)(n=0,1,2,3,…)
解析:(1)如果小球没有初速度则小球做简谐运动,简谐运动的周期为
小球运动到轨道最低点的时间
,(n=0,1,2,3,…)
(2)沿MN方向小球做匀速直线运动,则
L=v0t
解得
,(n=0,1,2,3,…)
15.(1)T=0.4πs;L=0.4m(2)0.089m/s;(3)0.495N
解析:(1)由F-t图可得
T=0.4πs
由
得
L=0.4m
(2)由F-t图可得,摆球运动到最低点时细线的拉力
Fmax=0.510N
此时有
Fmax-mg=m
解得
v=0.089m/s
(3)A→B机械能守恒
Fmin=mgcos
解得
Fmin=0.495N
答案第1页,共2页
答案第1页,共2页
