同步课时精练(十四)4.1光的折射(后附解析)
文档属性
| 名称 | 同步课时精练(十四)4.1光的折射(后附解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-05 18:55:57 | ||
图片预览


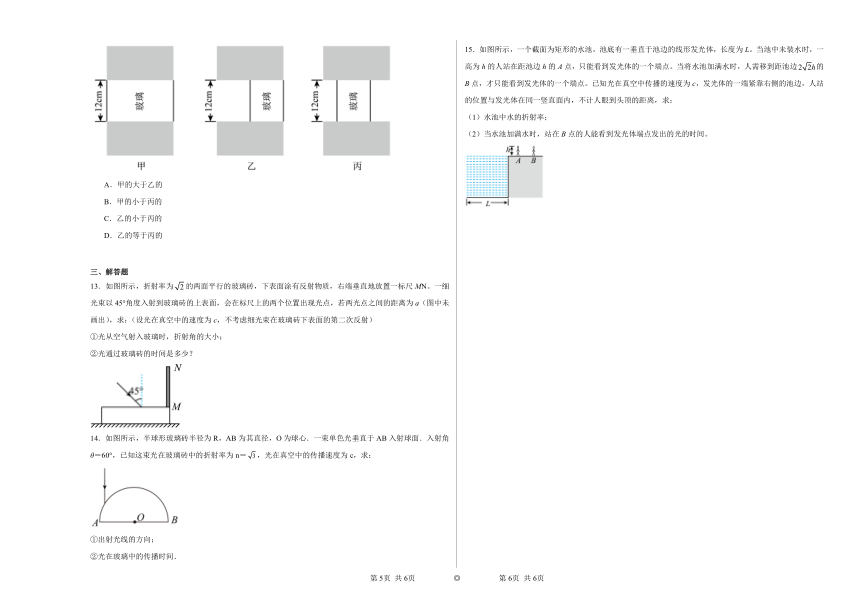


文档简介
同步课时精练(十四)4.1 光的折射(后附解析)
一、单选题
1.如图,一束单色光射向圆柱形玻璃砖的A点,已知其入射角为i,折射角为r,玻璃砖的折射率为,则( )
A.要使单色光进入玻璃砖,入射角i必须大于
B.选择合适的入射角i,可使单色光在玻璃砖内发射全反射
C.单色光第一次从玻璃砖射出时,光相对A点入射时方向改变
D.单色光第N次到达玻璃砖界面并射出时,光相对A点入射时方向改变
2.现在部分宾馆的卫生间有一种化妆镜,当对着它照镜子时,能看到自己面部更细微处。这种化妆镜应该是一个( )
A.平面镜 B.凸面镜 C.凹面镜 D.凸透镜
3.如图所示,一束平行复色光被玻璃三棱镜折射后分解为互相分离的红、黄、蓝三色光,分别照射到相同的三块金属板上,则可知( )
A.照射到板a上的光一定是蓝色光
B.照射到板c上的光在棱镜中传播速度最小
C.照射到板a上的光波长最长
D.照射到板c上的光折射率最大
4.如图所示,一束单色光从介质1射入介质2,在介质1、2中的波长分别为λ1、λ2,频率分别为f1、f2,则( )
A. B.
C. D.
5.如图所示,普通的 DVD采用红色激光器作为读写光源,而蓝光光盘(BD-ROM)则采用蓝色激光器, 由于读取激光的波长越短,则盘的记录层记录的最小凹坑长度越小,所以蓝光光盘单面最高容量比普通DVD 存储量大得多,下列说法中正确的是( )
A.红光频率高,蓝光频率低
B.在光盘的透明光学传输介质层中,红光束比蓝光束传播速度更快
C.若红蓝光束先后通过同一单缝衍射装置,红蓝光束的中央亮纹一样宽
D.蓝光和红光的复合光经过三棱镜折射后,红光偏折程度较大
6.“B超”可用于探测人体内脏的病变状况.下图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为(式中是入射角,是折射角, 、 分别为超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同.已知,入射点与出射点之间的距离是d,入射角为i,肿瘤的反射面恰好与肝脏表面平行,则肿瘤离肝脏表面的深度h为( )
A. B.
C. D.
7.内径为、外径为的透明介质半球壳的折射率,如图所示为其截面示意图。现将点光源放在处,点在点正上方内壳上,光射向外壳经过折射后射出球壳(不考虑光的反射),已知光在真空中的传播速度为。则介质球壳外表面发光区域在截面上形成的弧长为( )
A. B. C. D.
8.半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线,足够大的光屏PQ与直径MN垂直并接触于N点,已知半圈形玻璃砖的半径R=15cm,折射率。一细束激光沿半径方向射向圆心O点,入射光线与OO'夹角θ=30°,光屏PQ上出现两个光斑,则这两个光斑之间的距离为( )
A.cm B.cm C.cm D.cm
二、多选题
9.如图所示,一细束白光从左侧照射到三棱镜上后,在三棱镜的右侧的光屏上的M、N两点间形成一条彩色光带,则下列说法正确的是( )
A.M处是紫色,N处是红色
B.玻璃对M处光的临界角大于N处光的临界角
C.在真空中M处光的波长大于N处光的波长
D.在三棱镜中M处光的传播速率小于N处光的传播速率
10.如图所示,一块上、下表面平行的玻璃砖的厚度为L,玻璃砖的折射率,若光从上表面AB射入的入射角;光在真空中的速度为,则( )
A.折射角
B.光在玻璃中传播的时间为
C.光在玻璃中传播的时间为
D.改变入射角i,光在下表面CD可能发生全反射
11.某同学做“测定玻璃的折射率”的实验时,用他测得的多组入射角i和折射角r,作出图像,如图所示。下列判断中正确的是( )
A.他做实验时,光线是由空气射入玻璃的
B.他做实验时,光线是由玻璃射入空气的
C.该玻璃的折射率为0.67
D.该玻璃的折射率为
12.为了从坦克内部观察外部目标,在厚度为20cm的坦克壁上开了一个直径为12cm的孔,若在孔内分别安装由同一材料制成的如图所示的三块玻璃,其中两块玻璃的厚度相同。坦克内的人在同一位置通过玻璃能看到的外界的角度范围是( )
A.甲的大于乙的
B.甲的小于丙的
C.乙的小于丙的
D.乙的等于丙的
三、解答题
13.如图所示,折射率为的两面平行的玻璃砖,下表面涂有反射物质,右端垂直地放置一标尺MN。一细光束以45°角度入射到玻璃砖的上表面,会在标尺上的两个位置出现光点,若两光点之间的距离为a(图中未画出),求:(设光在真空中的速度为c,不考虑细光束在玻璃砖下表面的第二次反射)
①光从空气射入玻璃时,折射角的大小;
②光通过玻璃砖的时间是多少?
14.如图所示,半球形玻璃砖半径为R,AB为其直径,O为球心.一束单色光垂直于AB入射球面.入射角θ=60°,已知这束光在玻璃砖中的折射率为n=,光在真空中的传播速度为c,求:
①出射光线的方向;
②光在玻璃中的传播时间.
15.如图所示,一个截面为矩形的水池,池底有一垂直于池边的线形发光体,长度为L。当池中未装水时,一高为h的人站在距池边h的A点,只能看到发光体的一个端点。当将水池加满水时,人需移到距池边的B点,才只能看到发光体的一个端点。已知光在真空中传播的速度为c,发光体的一端紧靠右侧的池边,人站的位置与发光体在同一竖直面内,不计人眼到头顶的距离,求:
(1)水池中水的折射率;
(2)当水池加满水时,站在B点的人能看到发光体端点发出的光的时间。
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
解析:A单色光进入玻璃砖,属于从光疏介质进入光密介质。对入射角没有要求。故A错误;
B光路图如图所示,根据光路图的对称性可知,单色光不可能在玻璃砖内发射全反射。故B错误;
C由光路图可知,单色光第一次从玻璃砖射出时,光相对A点入射时方向改变,则根据几何关系有
故C正确;
D由光路图可知,单色光第N次到达玻璃砖界面并射出时,光相对A点入射时方向改变。故D错误。
答案:C。
2.C
解析:化妆镜利用的是光的反射,因此应该是面镜。
当对着它照镜子时,能看到自己面部更细微处,说明能成放大的像,凹面镜在物距<焦距时成正立放大的虚像。
答案:C。
3.A
解析:A.由图知,三种色光,a的偏折程度最大,c的偏折程度最小,知a的折射率最大,c的折射率最小。则a的频率最大,c的频率最小。所以c光应是红光,a光是蓝光。故A正确;
B.c的折射率最小,根据分析可知,c光在棱镜中传播速度最大。故B错误;
C.照射到板a上的光频率最大,,波长最短,故C错误;
D.照射到板c上的光折射率最小,故D错误。
答案:A。
4.B
解析:根据折射定律可知折射率小的介质光线与法线的夹角大,因此
由
可得
因为光从一种介质进入另一种介质时频率不变,即
根据
可知波长与波速成正比,即
答案:B。
5.B
解析:A.红光频率低,蓝光频率高,A错误;
B.根据
在光盘的透明光学传输介质层中,红光束的折射率小,红光比蓝光束传播速度更快,B正确;
C.若红蓝光束先后通过同一单缝衍射装置,红光的波长比蓝光长,红光的条纹宽,所以红蓝光束的中央亮纹不一样宽,红光的中央亮纹宽,C错误;
D.蓝光和红光的复合光经过三棱镜折射后,红光的折射率较小,偏折程度较小,D错误。
答案:B。
6.D
解析:
设光线射入肝脏后的折射角为,则由
可得
即
则
根据几何知识可得
联立几式得
答案:D。
7.A
解析:光从介质中射向真空,发生全反射的临界角C满足
解得
光源放于P点处,假设其射出的光线在Q点恰好发生全反射,如图所示,则在三角形OPQ中,根据正弦定理有
解得
则
根据对称性可知若点光源放于P点处,则介质球壳外表面发光区域在截面上形成的弧长为
答案:A。
8.B
解析:画出光路图如图所示
设折射角为γ,根据折射定律
则得
解得
γ=60°
根据几何关系,两个光斑之间的距离为
答案:B。
9.BC
解析:A.三棱镜对不同色光的偏折程度不同,其中对紫光的偏折大于对红光的偏折,即M处是红色,N处是紫色。故A错误;
B.三棱镜对M处的光偏折小,则其折射率小,根据临界角公式
可知,玻璃对M处光的临界角大于N处光的临界角。故B正确;
C.M处的光折射率小,则其频率小,根据公式
可知,在真空中处M光的波长大于N处光的波长。故C正确;
D.根据公式
可知,在三棱镜中M处光的传播速率大于N处光的传播速率。故D错误。
答案:BC。
10.AC
解析:由得:sinr=,得 r=30°。故A正确。光在玻璃中传播的速度为 v=c/n,由几何知识可知光在玻璃中传播的路程为,则光在玻璃中传播的时间为,故B错误,C正确。由于光在CD面上的入射角等于光在AB面上的折射角,根据光路可逆性原理得知光一定能从CD面射出,故D错误。答案:AC。
点睛:解决本题的关键是掌握折射率的两个公式和v=c/n,运用光路可逆性分析玻璃砖的光学特性。
11.AD
解析:AB.由图可知,入射角的正弦大于折射角的正弦,则入射角大于折射角,可知光线是由空气射入玻璃的,故A正确,B错误;
CD.根据折射定律得
故C错误,D正确。
答案:AD。
12.AD
解析:光线穿过玻璃砖后,出射光线和入射光线平行,光路图如图所示,图甲中的在玻璃砖中的入射角大于图乙、图丙中玻璃砖中的入射角,根据折射定律,射入空气的折射角图甲最大,根据光的可逆原理,知图甲观察到的角度范围最大.
由图可知,出射光线和入射光线平行,在图乙和图丙中,由几何关系知,两光线在玻璃砖中的入射角相等,则在空气中的折射角也相等,即图乙和图丙观察的范围相同。
答案:AD。
13.①30°;②
解析:①如图由光的折射定律
得
r=30°
②由几何关系可得:在玻璃砖内的光线与玻璃砖的上面构成等边三角形,其边长等于a
光在玻璃中的速度为
所以有
14.①出射光线与AB夹角为30°②
解析:①由折射定律
解得:α=30°
由几何关系可知△OCD为等边三角形
光线在AB面上的入射角β=30°
解得:γ=60°,即出射光线与AB夹角为30°
②由几何关系可知:CD=OD=
光在玻璃中的传播速度
光在玻璃中的传播时间
解得:
15.(1);(2)
解析:(1)水池加满水时,设在水中的光线与竖直方向的夹角为r,在空气中的光线与竖直方向夹角为i,其光路图如图所示,由几何关系得
由折射定律可得水池中水的折射率为
(2)水池加满水时,光在水中传播的速率为
光在水中传播的时间为
光在空气中传播的时间为
站在B点的人能看到发光体端点发出的光的时间为
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,一束单色光射向圆柱形玻璃砖的A点,已知其入射角为i,折射角为r,玻璃砖的折射率为,则( )
A.要使单色光进入玻璃砖,入射角i必须大于
B.选择合适的入射角i,可使单色光在玻璃砖内发射全反射
C.单色光第一次从玻璃砖射出时,光相对A点入射时方向改变
D.单色光第N次到达玻璃砖界面并射出时,光相对A点入射时方向改变
2.现在部分宾馆的卫生间有一种化妆镜,当对着它照镜子时,能看到自己面部更细微处。这种化妆镜应该是一个( )
A.平面镜 B.凸面镜 C.凹面镜 D.凸透镜
3.如图所示,一束平行复色光被玻璃三棱镜折射后分解为互相分离的红、黄、蓝三色光,分别照射到相同的三块金属板上,则可知( )
A.照射到板a上的光一定是蓝色光
B.照射到板c上的光在棱镜中传播速度最小
C.照射到板a上的光波长最长
D.照射到板c上的光折射率最大
4.如图所示,一束单色光从介质1射入介质2,在介质1、2中的波长分别为λ1、λ2,频率分别为f1、f2,则( )
A. B.
C. D.
5.如图所示,普通的 DVD采用红色激光器作为读写光源,而蓝光光盘(BD-ROM)则采用蓝色激光器, 由于读取激光的波长越短,则盘的记录层记录的最小凹坑长度越小,所以蓝光光盘单面最高容量比普通DVD 存储量大得多,下列说法中正确的是( )
A.红光频率高,蓝光频率低
B.在光盘的透明光学传输介质层中,红光束比蓝光束传播速度更快
C.若红蓝光束先后通过同一单缝衍射装置,红蓝光束的中央亮纹一样宽
D.蓝光和红光的复合光经过三棱镜折射后,红光偏折程度较大
6.“B超”可用于探测人体内脏的病变状况.下图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为(式中是入射角,是折射角, 、 分别为超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同.已知,入射点与出射点之间的距离是d,入射角为i,肿瘤的反射面恰好与肝脏表面平行,则肿瘤离肝脏表面的深度h为( )
A. B.
C. D.
7.内径为、外径为的透明介质半球壳的折射率,如图所示为其截面示意图。现将点光源放在处,点在点正上方内壳上,光射向外壳经过折射后射出球壳(不考虑光的反射),已知光在真空中的传播速度为。则介质球壳外表面发光区域在截面上形成的弧长为( )
A. B. C. D.
8.半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线,足够大的光屏PQ与直径MN垂直并接触于N点,已知半圈形玻璃砖的半径R=15cm,折射率。一细束激光沿半径方向射向圆心O点,入射光线与OO'夹角θ=30°,光屏PQ上出现两个光斑,则这两个光斑之间的距离为( )
A.cm B.cm C.cm D.cm
二、多选题
9.如图所示,一细束白光从左侧照射到三棱镜上后,在三棱镜的右侧的光屏上的M、N两点间形成一条彩色光带,则下列说法正确的是( )
A.M处是紫色,N处是红色
B.玻璃对M处光的临界角大于N处光的临界角
C.在真空中M处光的波长大于N处光的波长
D.在三棱镜中M处光的传播速率小于N处光的传播速率
10.如图所示,一块上、下表面平行的玻璃砖的厚度为L,玻璃砖的折射率,若光从上表面AB射入的入射角;光在真空中的速度为,则( )
A.折射角
B.光在玻璃中传播的时间为
C.光在玻璃中传播的时间为
D.改变入射角i,光在下表面CD可能发生全反射
11.某同学做“测定玻璃的折射率”的实验时,用他测得的多组入射角i和折射角r,作出图像,如图所示。下列判断中正确的是( )
A.他做实验时,光线是由空气射入玻璃的
B.他做实验时,光线是由玻璃射入空气的
C.该玻璃的折射率为0.67
D.该玻璃的折射率为
12.为了从坦克内部观察外部目标,在厚度为20cm的坦克壁上开了一个直径为12cm的孔,若在孔内分别安装由同一材料制成的如图所示的三块玻璃,其中两块玻璃的厚度相同。坦克内的人在同一位置通过玻璃能看到的外界的角度范围是( )
A.甲的大于乙的
B.甲的小于丙的
C.乙的小于丙的
D.乙的等于丙的
三、解答题
13.如图所示,折射率为的两面平行的玻璃砖,下表面涂有反射物质,右端垂直地放置一标尺MN。一细光束以45°角度入射到玻璃砖的上表面,会在标尺上的两个位置出现光点,若两光点之间的距离为a(图中未画出),求:(设光在真空中的速度为c,不考虑细光束在玻璃砖下表面的第二次反射)
①光从空气射入玻璃时,折射角的大小;
②光通过玻璃砖的时间是多少?
14.如图所示,半球形玻璃砖半径为R,AB为其直径,O为球心.一束单色光垂直于AB入射球面.入射角θ=60°,已知这束光在玻璃砖中的折射率为n=,光在真空中的传播速度为c,求:
①出射光线的方向;
②光在玻璃中的传播时间.
15.如图所示,一个截面为矩形的水池,池底有一垂直于池边的线形发光体,长度为L。当池中未装水时,一高为h的人站在距池边h的A点,只能看到发光体的一个端点。当将水池加满水时,人需移到距池边的B点,才只能看到发光体的一个端点。已知光在真空中传播的速度为c,发光体的一端紧靠右侧的池边,人站的位置与发光体在同一竖直面内,不计人眼到头顶的距离,求:
(1)水池中水的折射率;
(2)当水池加满水时,站在B点的人能看到发光体端点发出的光的时间。
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
解析:A单色光进入玻璃砖,属于从光疏介质进入光密介质。对入射角没有要求。故A错误;
B光路图如图所示,根据光路图的对称性可知,单色光不可能在玻璃砖内发射全反射。故B错误;
C由光路图可知,单色光第一次从玻璃砖射出时,光相对A点入射时方向改变,则根据几何关系有
故C正确;
D由光路图可知,单色光第N次到达玻璃砖界面并射出时,光相对A点入射时方向改变。故D错误。
答案:C。
2.C
解析:化妆镜利用的是光的反射,因此应该是面镜。
当对着它照镜子时,能看到自己面部更细微处,说明能成放大的像,凹面镜在物距<焦距时成正立放大的虚像。
答案:C。
3.A
解析:A.由图知,三种色光,a的偏折程度最大,c的偏折程度最小,知a的折射率最大,c的折射率最小。则a的频率最大,c的频率最小。所以c光应是红光,a光是蓝光。故A正确;
B.c的折射率最小,根据分析可知,c光在棱镜中传播速度最大。故B错误;
C.照射到板a上的光频率最大,,波长最短,故C错误;
D.照射到板c上的光折射率最小,故D错误。
答案:A。
4.B
解析:根据折射定律可知折射率小的介质光线与法线的夹角大,因此
由
可得
因为光从一种介质进入另一种介质时频率不变,即
根据
可知波长与波速成正比,即
答案:B。
5.B
解析:A.红光频率低,蓝光频率高,A错误;
B.根据
在光盘的透明光学传输介质层中,红光束的折射率小,红光比蓝光束传播速度更快,B正确;
C.若红蓝光束先后通过同一单缝衍射装置,红光的波长比蓝光长,红光的条纹宽,所以红蓝光束的中央亮纹不一样宽,红光的中央亮纹宽,C错误;
D.蓝光和红光的复合光经过三棱镜折射后,红光的折射率较小,偏折程度较小,D错误。
答案:B。
6.D
解析:
设光线射入肝脏后的折射角为,则由
可得
即
则
根据几何知识可得
联立几式得
答案:D。
7.A
解析:光从介质中射向真空,发生全反射的临界角C满足
解得
光源放于P点处,假设其射出的光线在Q点恰好发生全反射,如图所示,则在三角形OPQ中,根据正弦定理有
解得
则
根据对称性可知若点光源放于P点处,则介质球壳外表面发光区域在截面上形成的弧长为
答案:A。
8.B
解析:画出光路图如图所示
设折射角为γ,根据折射定律
则得
解得
γ=60°
根据几何关系,两个光斑之间的距离为
答案:B。
9.BC
解析:A.三棱镜对不同色光的偏折程度不同,其中对紫光的偏折大于对红光的偏折,即M处是红色,N处是紫色。故A错误;
B.三棱镜对M处的光偏折小,则其折射率小,根据临界角公式
可知,玻璃对M处光的临界角大于N处光的临界角。故B正确;
C.M处的光折射率小,则其频率小,根据公式
可知,在真空中处M光的波长大于N处光的波长。故C正确;
D.根据公式
可知,在三棱镜中M处光的传播速率大于N处光的传播速率。故D错误。
答案:BC。
10.AC
解析:由得:sinr=,得 r=30°。故A正确。光在玻璃中传播的速度为 v=c/n,由几何知识可知光在玻璃中传播的路程为,则光在玻璃中传播的时间为,故B错误,C正确。由于光在CD面上的入射角等于光在AB面上的折射角,根据光路可逆性原理得知光一定能从CD面射出,故D错误。答案:AC。
点睛:解决本题的关键是掌握折射率的两个公式和v=c/n,运用光路可逆性分析玻璃砖的光学特性。
11.AD
解析:AB.由图可知,入射角的正弦大于折射角的正弦,则入射角大于折射角,可知光线是由空气射入玻璃的,故A正确,B错误;
CD.根据折射定律得
故C错误,D正确。
答案:AD。
12.AD
解析:光线穿过玻璃砖后,出射光线和入射光线平行,光路图如图所示,图甲中的在玻璃砖中的入射角大于图乙、图丙中玻璃砖中的入射角,根据折射定律,射入空气的折射角图甲最大,根据光的可逆原理,知图甲观察到的角度范围最大.
由图可知,出射光线和入射光线平行,在图乙和图丙中,由几何关系知,两光线在玻璃砖中的入射角相等,则在空气中的折射角也相等,即图乙和图丙观察的范围相同。
答案:AD。
13.①30°;②
解析:①如图由光的折射定律
得
r=30°
②由几何关系可得:在玻璃砖内的光线与玻璃砖的上面构成等边三角形,其边长等于a
光在玻璃中的速度为
所以有
14.①出射光线与AB夹角为30°②
解析:①由折射定律
解得:α=30°
由几何关系可知△OCD为等边三角形
光线在AB面上的入射角β=30°
解得:γ=60°,即出射光线与AB夹角为30°
②由几何关系可知:CD=OD=
光在玻璃中的传播速度
光在玻璃中的传播时间
解得:
15.(1);(2)
解析:(1)水池加满水时,设在水中的光线与竖直方向的夹角为r,在空气中的光线与竖直方向夹角为i,其光路图如图所示,由几何关系得
由折射定律可得水池中水的折射率为
(2)水池加满水时,光在水中传播的速率为
光在水中传播的时间为
光在空气中传播的时间为
站在B点的人能看到发光体端点发出的光的时间为
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
