18.1勾股定理
图片预览





文档简介
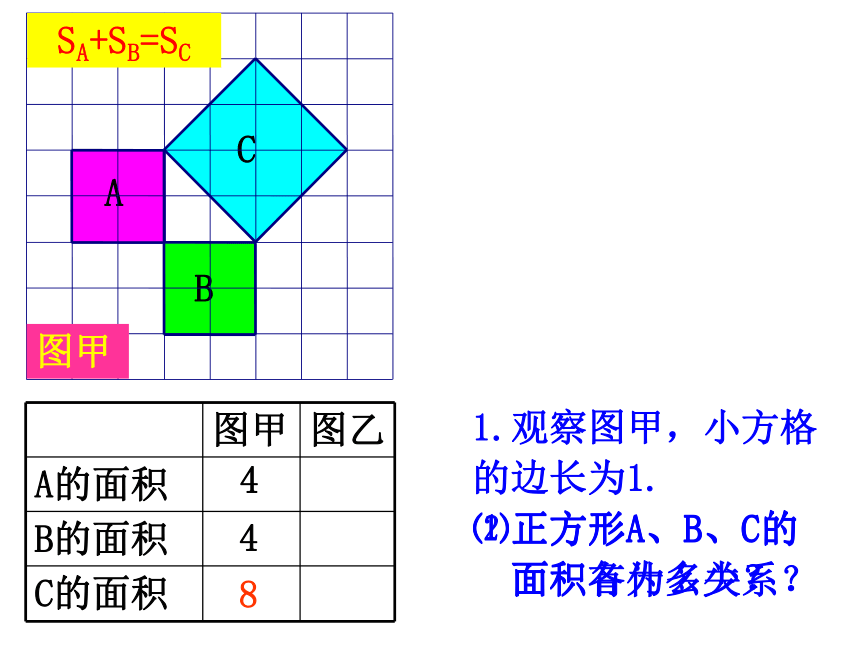
课件47张PPT。18.1 勾股定理南门学校 八年(1)(2)班448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
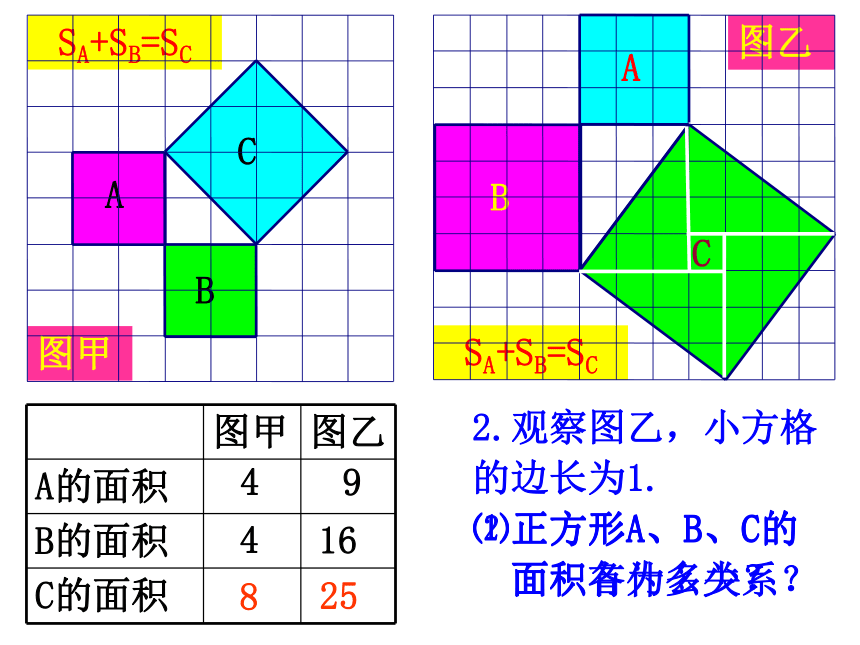
面积有什么关系?C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625SA+SB=SC⑵正方形A、B、C的
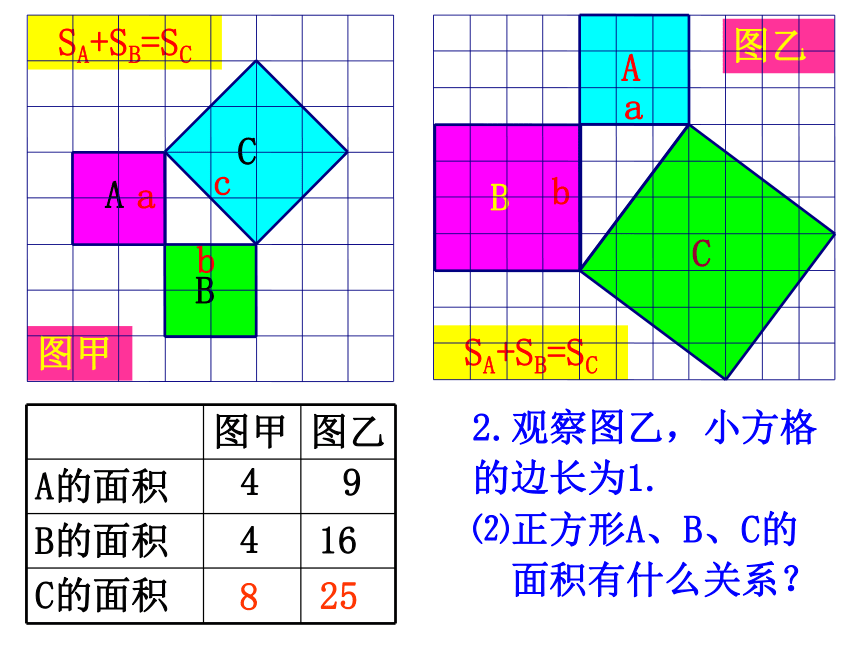
面积有什么关系?448SA+SB=SC图甲图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
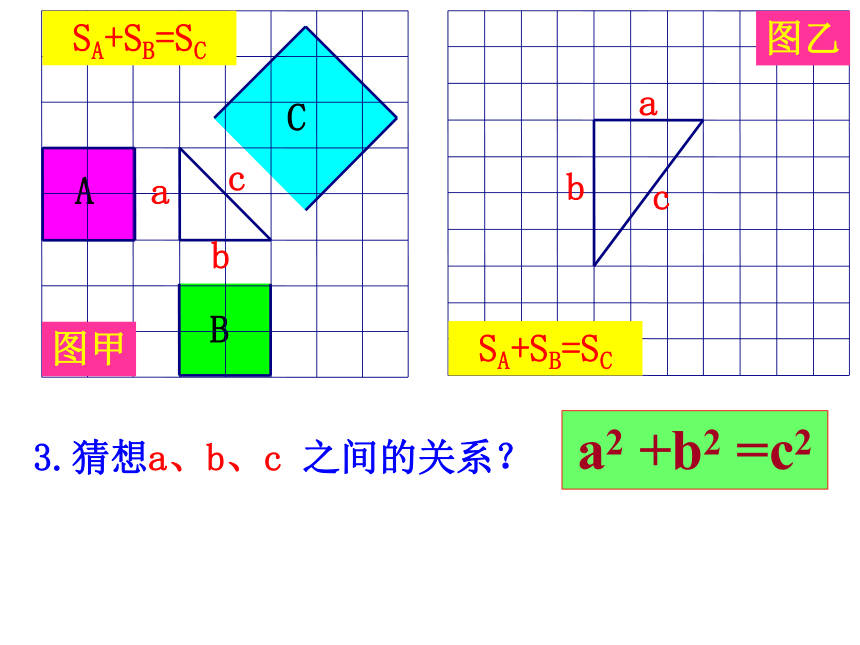
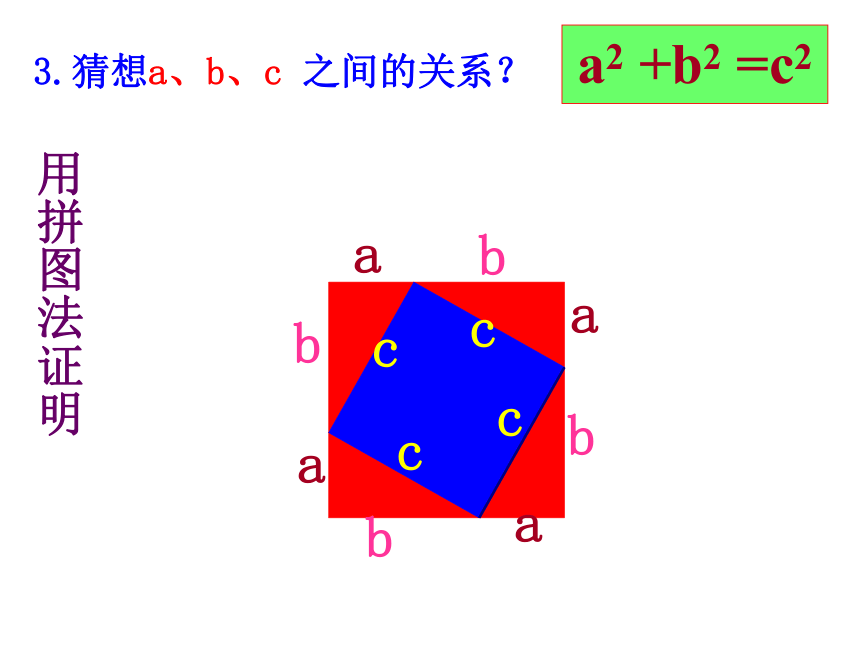
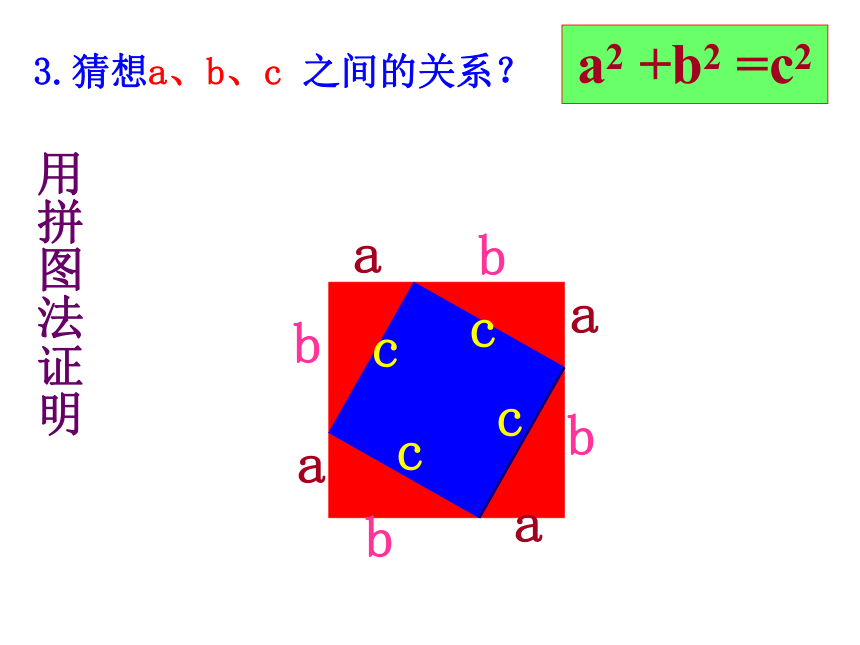
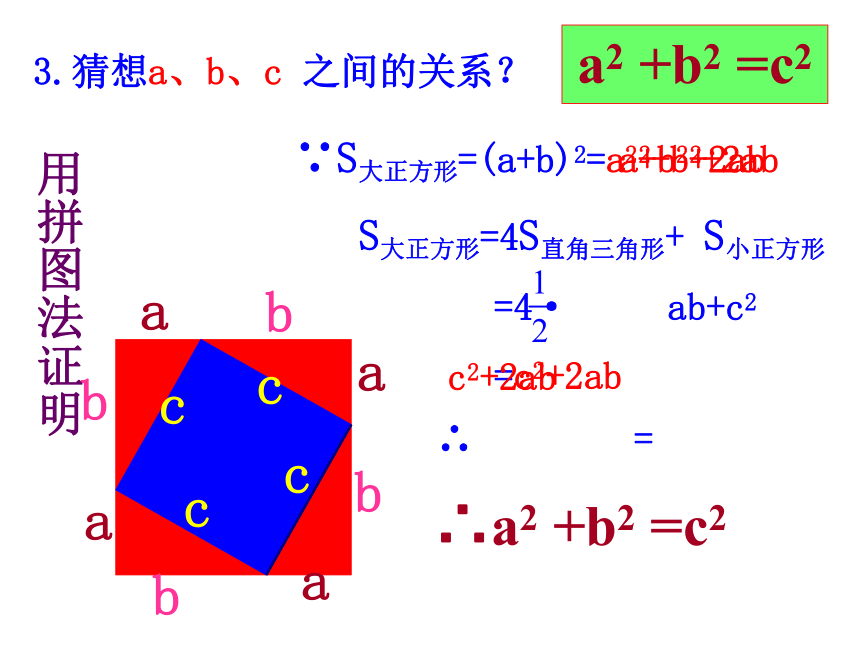
面积有什么关系?448SA+SB=SC图甲abcabc3.猜想a、b、c 之间的关系?a2 +b2 =c2aaaabbbbcccc用拼图法证明用拼图法证明用拼图法证明∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab=c2+2ab∴a2 +b2 =c2a2+b2+2abc2+2ab勾股定理(毕达哥拉斯定理) (gou-gu theorem) 如果直角三角形两直角边分别为a, b,斜边为c,那么ac勾弦b股 例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C342、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米1312?A3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8BB 6、8、10D 8、10、125 或 4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 . 例2.已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
(2)求S△ABC .例题分析36? 已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练1046810xEFDCBA8-x8-x练习:
1、求下列图中字母所表示的正方形的面积=625=144探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m 课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在? ABC中, ∠C=90°,AC=6,CB=8,则
?ABC面积为_____,斜边为上的高为______.??244.8ABCD二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.6841244.8DA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形扩展利用勾股定理作出长为
的线段.11 4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD7 .观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
84859、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA二、圆柱(锥)中的最值问题例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.四、长方体中的最值问题8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C10、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC2. 如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )
A.7m B.8m C.9m D.10m8m8m2m7、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习4、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=81.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 ,
AD = 3,AB = 4,BC = 12,
求CD;
练习2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49小结:1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)A的面积+B的面积=C的面积a2+b2=c2实际问题直角三角
形的问题数学问题利用勾
股定理抽象归类解决建构活动聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。(1)(2)数学奇闻有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)ABC20尺3×7=21(尺)聪明的葛藤证法四:(伽菲尔德证法1876年) 如图,Rt△ABE≌Rt△ECD,
可知∠AED=90°;证法五:(欧几里得证法公元前3世纪)“新娘的轿椅”或“修士的头巾” 如图,Rt△ ABC中,∠ACB=90°,四边形ACHK、BCGF、ABED都是正方形,CN⊥DE,连接BK、CD。同理:S 正方形BCGF = S 四边形BENM 再 见
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
面积有什么关系?C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图甲图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图甲abcabc3.猜想a、b、c 之间的关系?a2 +b2 =c2aaaabbbbcccc用拼图法证明用拼图法证明用拼图法证明∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab=c2+2ab∴a2 +b2 =c2a2+b2+2abc2+2ab勾股定理(毕达哥拉斯定理) (gou-gu theorem) 如果直角三角形两直角边分别为a, b,斜边为c,那么ac勾弦b股 例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C342、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米1312?A3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8BB 6、8、10D 8、10、125 或 4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 . 例2.已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
(2)求S△ABC .例题分析36? 已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练1046810xEFDCBA8-x8-x练习:
1、求下列图中字母所表示的正方形的面积=625=144探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m 课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在? ABC中, ∠C=90°,AC=6,CB=8,则
?ABC面积为_____,斜边为上的高为______.??244.8ABCD二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.6841244.8DA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形扩展利用勾股定理作出长为
的线段.11 4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD7 .观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
84859、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA二、圆柱(锥)中的最值问题例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.四、长方体中的最值问题8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C10、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC2. 如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )
A.7m B.8m C.9m D.10m8m8m2m7、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习4、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=81.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 ,
AD = 3,AB = 4,BC = 12,
求CD;
练习2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49小结:1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)A的面积+B的面积=C的面积a2+b2=c2实际问题直角三角
形的问题数学问题利用勾
股定理抽象归类解决建构活动聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。(1)(2)数学奇闻有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)ABC20尺3×7=21(尺)聪明的葛藤证法四:(伽菲尔德证法1876年) 如图,Rt△ABE≌Rt△ECD,
可知∠AED=90°;证法五:(欧几里得证法公元前3世纪)“新娘的轿椅”或“修士的头巾” 如图,Rt△ ABC中,∠ACB=90°,四边形ACHK、BCGF、ABED都是正方形,CN⊥DE,连接BK、CD。同理:S 正方形BCGF = S 四边形BENM 再 见
