第4章 相交线与平行线 小结与复习 课件(共21张PPT)
文档属性
| 名称 | 第4章 相交线与平行线 小结与复习 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-06 10:08:22 | ||
图片预览





文档简介
(共21张PPT)
小结与复习
第4章 相交线与平行线
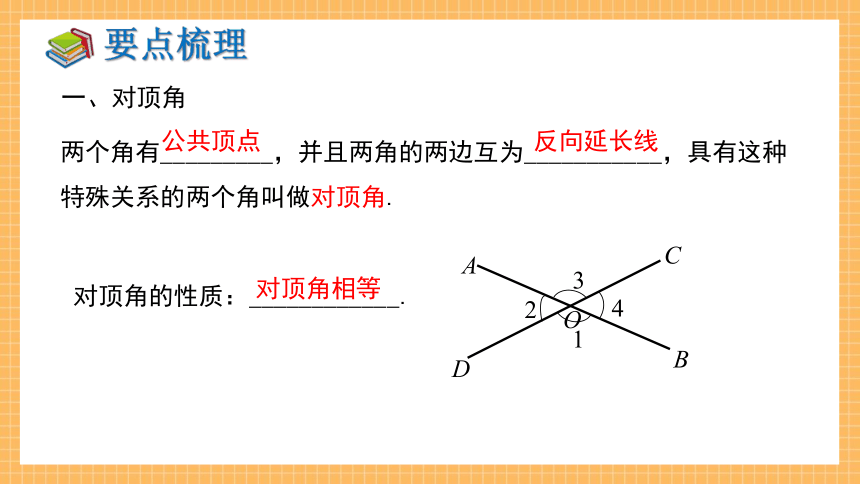
一、对顶角
两个角有_________,并且两角的两边互为___________,具有这种特殊关系的两个角叫做对顶角.
对顶角的性质:____________.
A
O
C
B
D
1
3
2
4
公共顶点
反向延长线
对顶角相等
二、垂线
两条直线相交所成的四个角中,有一个角是_____时,这两条直线互相垂直,其中一条直线叫另一条直线的______,它们的交点叫______.
1. 垂线的定义
2. 经过直线上或直线外一点,_________一条直线与已
知直线垂直.
4. 直线外一点到这条直线的垂线段的______,叫做点到
直线的距离.
3. 直线外一点与直线上各点的所有连线中,______最短.
有且只有
垂线段
长度
直角
垂线
垂足
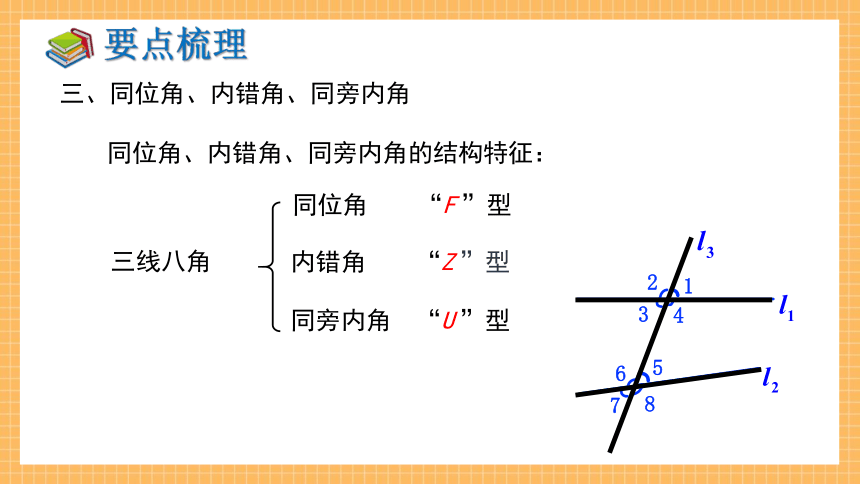
同位角、内错角、同旁内角的结构特征:
同位角 “F ”型
内错角 “Z ”型
同旁内角 “U ”型
三、同位角、内错角、同旁内角
三线八角
四、平行线
1. 在同一平面内,___________的两条直线叫做平行线.
3. 平行于同一条直线的两条直线______.
2. 经过直线外一点,________一条直线与已知直线平行.
4. 平行线的判定与性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
没有公共点
有且只有
平行
五、平移
1. 平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
2. 平移的性质:
(1) 平移前后的图形的形状,大小和朝向完全相同;
(2) 对应线段平行(或在同一条直线上)且相等;
(3) 对应点所连线段平行(或在同一条直线上)且相等.
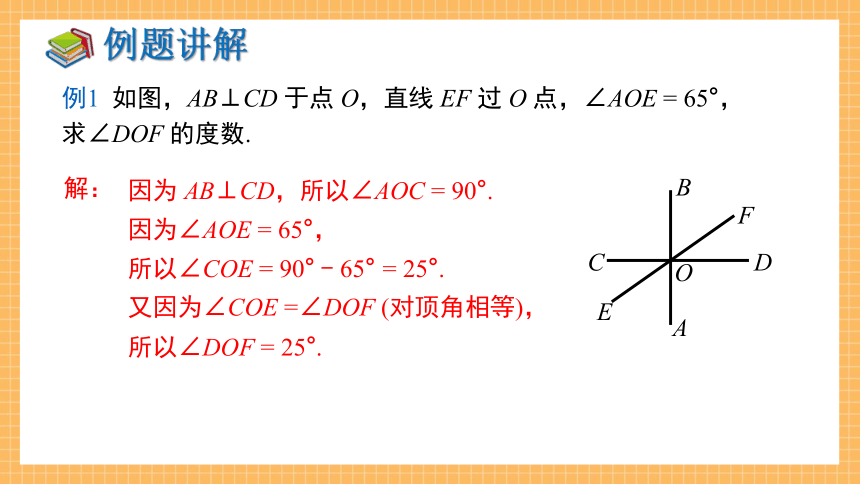
例1 如图,AB⊥CD 于点 O,直线 EF 过 O 点,∠AOE = 65°,求∠DOF 的度数.
解:
因为 AB⊥CD,所以∠AOC = 90°.
因为∠AOE = 65°,
所以∠COE = 90° - 65° = 25°.
又因为∠COE =∠DOF (对顶角相等),
所以∠DOF = 25°.
B
A
C
D
F
E
O
1. 如图,直线 AB、CD 相交于点 O,OE⊥AB 于点 O,OB 平分∠DOF,∠DOE = 50°,求∠AOC、∠EOF、∠COF 的度数.
解:因为 AB⊥OE,所以∠EOB = 90°.
因为∠DOE = 50°,所以∠DOB = 40°.
所以∠AOC =∠DOB = 40°.
又因为 OB 平分∠DOF,
所以∠BOF =∠DOB = 40°.
所以∠EOF =∠EOB +∠BOF = 90° + 40° = 130°.
所以∠COF =∠COD-∠DOF = 180°-80° = 100°.
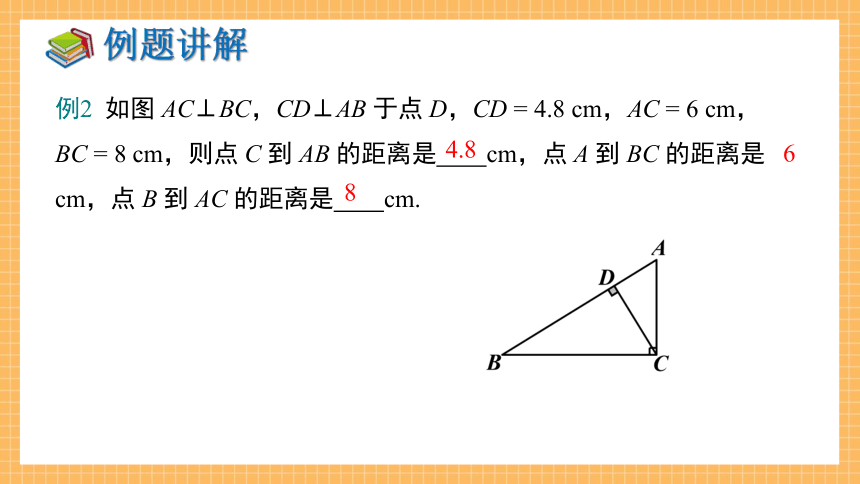
例2 如图 AC⊥BC,CD⊥AB 于点 D,CD = 4.8 cm,AC = 6 cm,BC = 8 cm,则点 C 到 AB 的距离是 cm,点 A 到 BC 的距离是 cm,点 B 到 AC 的距离是 cm.
4.8
6
8
解:连接 AB,作 BC⊥MN,垂足为 C,
线段 AB 和 BC 就是符合题意的线路图.
因为从 A 到 B,线段 AB 最短,
从 B 到 MN,垂线段 BC 最短,所以 AB+BC 最短.
2. 如图所示,修一条路将 B 村庄与 A 村庄及公路 MN 连起来,怎样修才能使所修的公路最短?画出线路图,并说明理由.
与垂线段有关的作图,一般是过一点作已知直线的垂线,作图的依据是“垂线段最短”.
例3 (1)如图所示,∠1 = 72°,∠2 = 72°,∠3 = 60°,求∠4 的度数;
解:因为∠1 =∠2 = 72°,
所以 a∥b (内错角相等,两直线平行).
所以∠3 +∠4 = 180°
(两直线平行,同旁内角互补).
因为∠3 = 60°,所以∠4 = 120°.
a
b
解:因为∠DAC =∠ACB (已知),
所以 AD∥BC (内错角相等,两直线平行).
因为∠D +∠DFE = 180° (已知),
所以 AD∥EF (同旁内角互补,两直线平行).
所以 EF∥BC (平行于同一条直线的两条直线互相平行).
(2)已知∠DAC =∠ACB,∠D +∠DFE = 180°,试说
明:EF∥BC.
A
B
C
D
E
F
3. 如图 (1),已知 AB∥CD,∠1 = 30°,∠2 = 90°,则∠3 = ____°.
4. 如图 (2),若 AE∥CD,∠EBF = 135°,∠BFD = 60°,
则∠D = ( )
A. 75° B. 45° C. 30° D. 15°
60
D
图 (1)
图 (2)
例4 如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是 ( )
解析:紧扣平移的概念及性质解题.
D
A B C D
解:设∠1 的度数为 x°,则∠2 的度数为 x°,
∠3 的度数为 8x°,根据题意可得
x°+ x°+ 8x°= 180°,解得 x = 18.
即∠1 = ∠2 = 18°.
而∠4 = ∠1 +∠2(对顶角相等),
故∠4 = 36°.
例5 如图所示, 交于点 O,∠1 =∠2,∠3:∠1 =8:1,求∠4 的度数.
4
1
2
3
O
(
)
)
(
5. 如图所示,直线 AB 与 CD 交于点 O,
∠AOC:∠AOD = 2:3,求∠BOD 的度数.
A
B
C
D
O
答案:72°
方法归纳 利用方程思想解决问题 ,是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便. 在有关线段或角的求值问题中它的应用非常广泛.
平面内两条直线的位置关系
两条直线相交
对顶角相等
垂线,点到直线的距离
两条直线被第
三条直线所截
两直线平行
两直线平行的判定
两直线平行的性质
同位角、内错角、同旁内角
两直线平行的判定
同位角相等,两直线平行
同旁内角互补,两直线平行
两直线平行的性质
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
两直线平行,内错角相等
平行线间的公垂线段(距离)都相等
见教材章末练习题
小结与复习
第4章 相交线与平行线
一、对顶角
两个角有_________,并且两角的两边互为___________,具有这种特殊关系的两个角叫做对顶角.
对顶角的性质:____________.
A
O
C
B
D
1
3
2
4
公共顶点
反向延长线
对顶角相等
二、垂线
两条直线相交所成的四个角中,有一个角是_____时,这两条直线互相垂直,其中一条直线叫另一条直线的______,它们的交点叫______.
1. 垂线的定义
2. 经过直线上或直线外一点,_________一条直线与已
知直线垂直.
4. 直线外一点到这条直线的垂线段的______,叫做点到
直线的距离.
3. 直线外一点与直线上各点的所有连线中,______最短.
有且只有
垂线段
长度
直角
垂线
垂足
同位角、内错角、同旁内角的结构特征:
同位角 “F ”型
内错角 “Z ”型
同旁内角 “U ”型
三、同位角、内错角、同旁内角
三线八角
四、平行线
1. 在同一平面内,___________的两条直线叫做平行线.
3. 平行于同一条直线的两条直线______.
2. 经过直线外一点,________一条直线与已知直线平行.
4. 平行线的判定与性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
没有公共点
有且只有
平行
五、平移
1. 平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
2. 平移的性质:
(1) 平移前后的图形的形状,大小和朝向完全相同;
(2) 对应线段平行(或在同一条直线上)且相等;
(3) 对应点所连线段平行(或在同一条直线上)且相等.
例1 如图,AB⊥CD 于点 O,直线 EF 过 O 点,∠AOE = 65°,求∠DOF 的度数.
解:
因为 AB⊥CD,所以∠AOC = 90°.
因为∠AOE = 65°,
所以∠COE = 90° - 65° = 25°.
又因为∠COE =∠DOF (对顶角相等),
所以∠DOF = 25°.
B
A
C
D
F
E
O
1. 如图,直线 AB、CD 相交于点 O,OE⊥AB 于点 O,OB 平分∠DOF,∠DOE = 50°,求∠AOC、∠EOF、∠COF 的度数.
解:因为 AB⊥OE,所以∠EOB = 90°.
因为∠DOE = 50°,所以∠DOB = 40°.
所以∠AOC =∠DOB = 40°.
又因为 OB 平分∠DOF,
所以∠BOF =∠DOB = 40°.
所以∠EOF =∠EOB +∠BOF = 90° + 40° = 130°.
所以∠COF =∠COD-∠DOF = 180°-80° = 100°.
例2 如图 AC⊥BC,CD⊥AB 于点 D,CD = 4.8 cm,AC = 6 cm,BC = 8 cm,则点 C 到 AB 的距离是 cm,点 A 到 BC 的距离是 cm,点 B 到 AC 的距离是 cm.
4.8
6
8
解:连接 AB,作 BC⊥MN,垂足为 C,
线段 AB 和 BC 就是符合题意的线路图.
因为从 A 到 B,线段 AB 最短,
从 B 到 MN,垂线段 BC 最短,所以 AB+BC 最短.
2. 如图所示,修一条路将 B 村庄与 A 村庄及公路 MN 连起来,怎样修才能使所修的公路最短?画出线路图,并说明理由.
与垂线段有关的作图,一般是过一点作已知直线的垂线,作图的依据是“垂线段最短”.
例3 (1)如图所示,∠1 = 72°,∠2 = 72°,∠3 = 60°,求∠4 的度数;
解:因为∠1 =∠2 = 72°,
所以 a∥b (内错角相等,两直线平行).
所以∠3 +∠4 = 180°
(两直线平行,同旁内角互补).
因为∠3 = 60°,所以∠4 = 120°.
a
b
解:因为∠DAC =∠ACB (已知),
所以 AD∥BC (内错角相等,两直线平行).
因为∠D +∠DFE = 180° (已知),
所以 AD∥EF (同旁内角互补,两直线平行).
所以 EF∥BC (平行于同一条直线的两条直线互相平行).
(2)已知∠DAC =∠ACB,∠D +∠DFE = 180°,试说
明:EF∥BC.
A
B
C
D
E
F
3. 如图 (1),已知 AB∥CD,∠1 = 30°,∠2 = 90°,则∠3 = ____°.
4. 如图 (2),若 AE∥CD,∠EBF = 135°,∠BFD = 60°,
则∠D = ( )
A. 75° B. 45° C. 30° D. 15°
60
D
图 (1)
图 (2)
例4 如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是 ( )
解析:紧扣平移的概念及性质解题.
D
A B C D
解:设∠1 的度数为 x°,则∠2 的度数为 x°,
∠3 的度数为 8x°,根据题意可得
x°+ x°+ 8x°= 180°,解得 x = 18.
即∠1 = ∠2 = 18°.
而∠4 = ∠1 +∠2(对顶角相等),
故∠4 = 36°.
例5 如图所示, 交于点 O,∠1 =∠2,∠3:∠1 =8:1,求∠4 的度数.
4
1
2
3
O
(
)
)
(
5. 如图所示,直线 AB 与 CD 交于点 O,
∠AOC:∠AOD = 2:3,求∠BOD 的度数.
A
B
C
D
O
答案:72°
方法归纳 利用方程思想解决问题 ,是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便. 在有关线段或角的求值问题中它的应用非常广泛.
平面内两条直线的位置关系
两条直线相交
对顶角相等
垂线,点到直线的距离
两条直线被第
三条直线所截
两直线平行
两直线平行的判定
两直线平行的性质
同位角、内错角、同旁内角
两直线平行的判定
同位角相等,两直线平行
同旁内角互补,两直线平行
两直线平行的性质
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
两直线平行,内错角相等
平行线间的公垂线段(距离)都相等
见教材章末练习题
