第七章 相交线与平行线 3 平行线的性质 第1课时 平行线的性质(含答案)
文档属性
| 名称 | 第七章 相交线与平行线 3 平行线的性质 第1课时 平行线的性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 09:13:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
3 平行线的性质
第1课时 平行线的性质
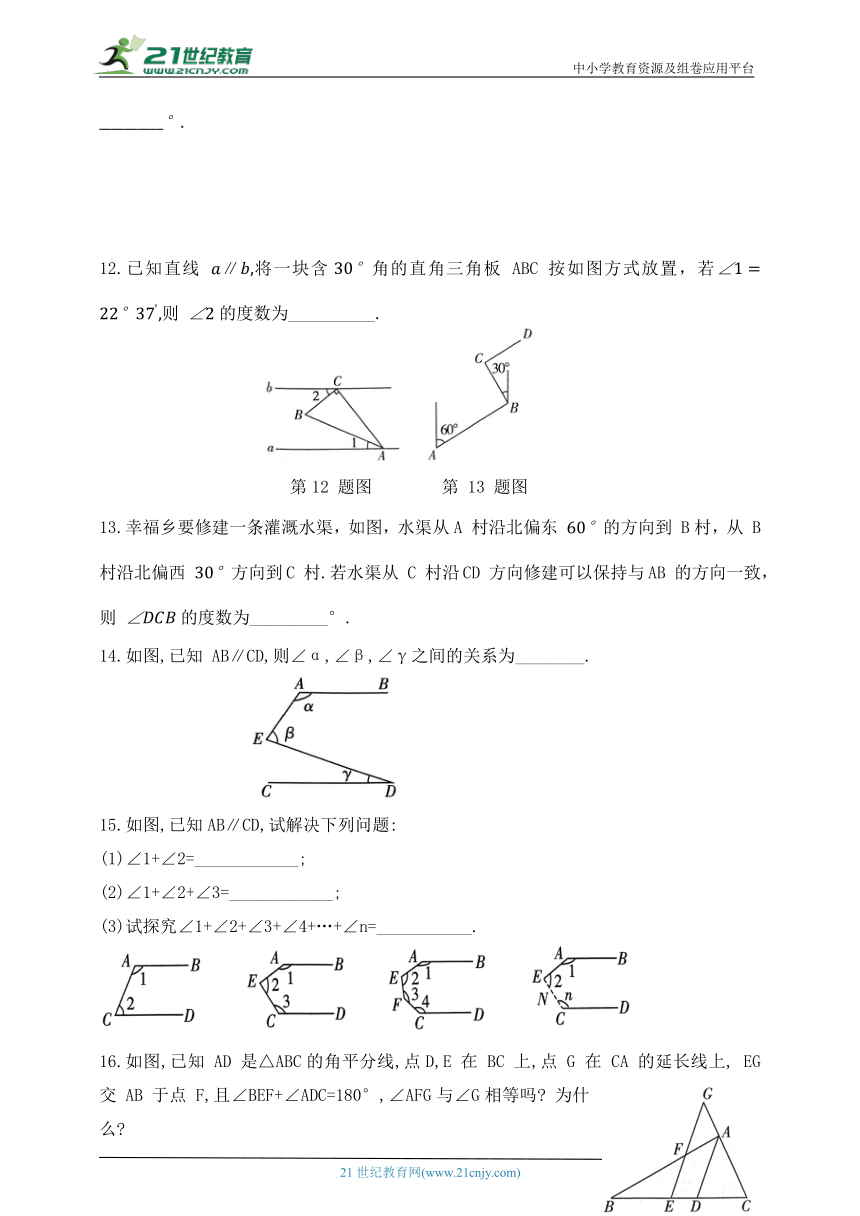
1.如图, ∥点 E 在AC 的延长线上,下列结论一定成立的是( )
C.∠1=∠2 D.∠3=∠4
第1题图 第 2 题图
2.如图,将一块含有 角的直角三角板的顶点放在直尺的一边上.若∠1=42°,则∠2 的度数是 ( )
A.72° B.92° C.102° D.108°
3.如图,烧杯内液体表面AB 与烧杯下底部 CD 平行,光线 EF 从液体中射向空气时发生折射,光线变成 FH,点 G 在射线 EF 上. 已知 则∠GFH的度数为 ( )
A.20° B.40° C.60° D.80°
第3 题图 第 4 题图
4把一块直角三角板和一把直尺如图放置,若 ,则∠2 的度数等于( )
A.65° B.55° C.45°
5.一辆汽车在笔直的公路上行驶,两次拐弯后,还在原来的方向上平行前进,那么这两次拐弯的角度应是 ( )
A.第一次右拐 第二次左拐 B.第一次左拐 第二次右拐
C.第一次左拐 第二次左拐 D.第一次右拐 第二次右拐
6.如图,已知 ∥∠A=25°,∠CDE=135°,则. 的度数是 ( )
A.45° B.60° C.70° D.90°
第 6 题图 第7题图
7.如图,直线 MN∥EF,直角三角形 ABC 的直角顶点 A 在直线 EF上,边 AB 与MN 相交于点D,若∠ADM=123°,则∠FAC的度数为 ( )
A.33° B.43° C.57° D.67°
8.一条两边沿互相平行的围巾按图所示折叠,已知∠DAB-∠ABC=8°,且 DF∥CG,则 ∠DAB+2∠ABC= ( )
A.130° B.131° C.132° D. 133°
第 8题 第 9 题图
9.如图,直线 把三角尺的直角顶点放在直线 b上,若 则
10.我们规定车辆在转弯时的转弯角是车辆原行驶路线与转弯后路线所成的角的外角.如图一辆车在一段绕山公路行驶(沿箭头方向)时,在点 B,C和D 处的转弯角分别是α,β和θ,且 ∥DE,则α,β和θ之间的数量关系是__________.
11.如图,把一张长方形纸片 ABCD沿EF 折叠后,点 D,C 分别在点 M,N 的位置上,EM 与BC 的交点为G,若 则
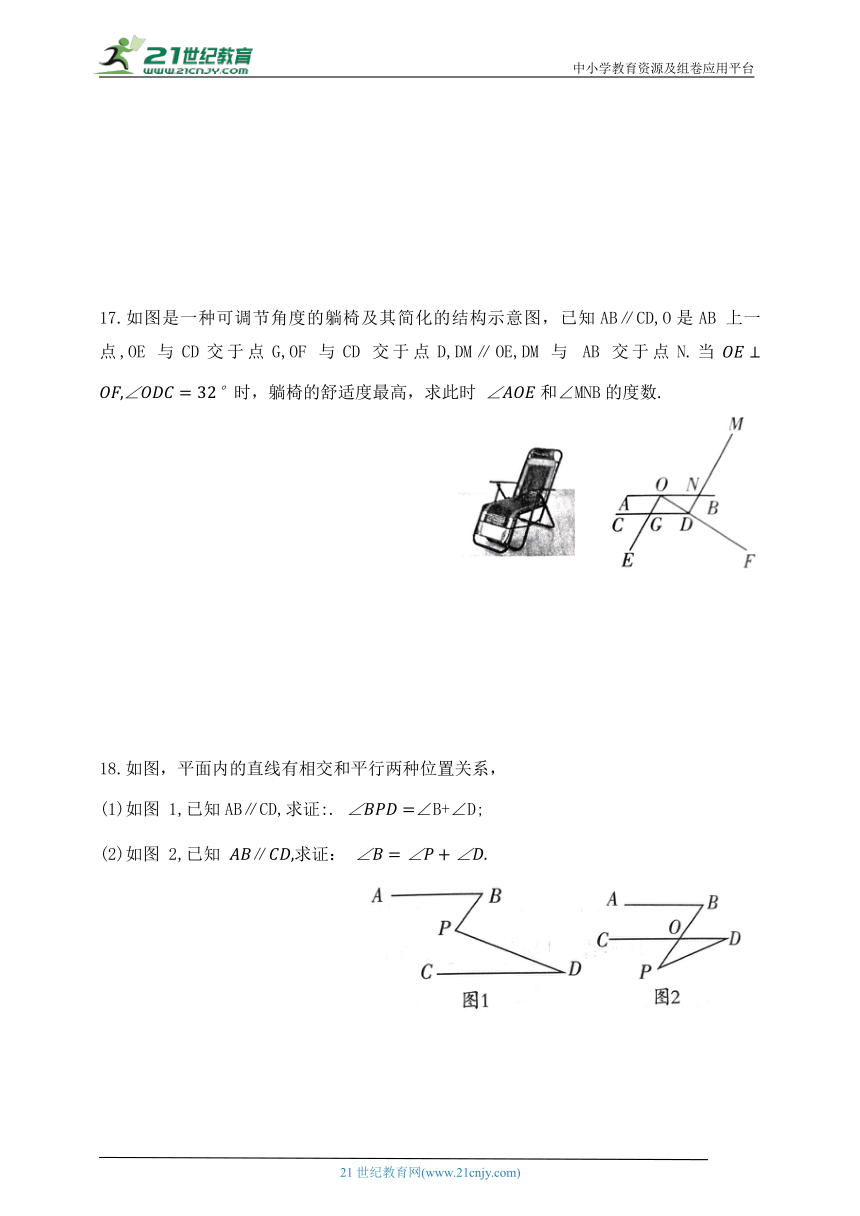
12.已知直线 ∥将一块含角的直角三角板 ABC 按如图方式放置,若则 的度数为__________.
第12 题图 第 13 题图
13.幸福乡要修建一条灌溉水渠,如图,水渠从A 村沿北偏东 的方向到 B村,从 B 村沿北偏西 方向到C 村.若水渠从 C 村沿CD 方向修建可以保持与AB 的方向一致,则 的度数为_________°.
14.如图,已知 AB∥CD,则∠α,∠β,∠γ之间的关系为________.
15.如图,已知AB∥CD,试解决下列问题:
(1)∠1+∠2=____________;
(2)∠1+∠2+∠3=____________;
(3)试探究∠1+∠2+∠3+∠4+…+∠n=___________.
16.如图,已知 AD 是△ABC的角平分线,点D,E 在 BC 上,点 G 在 CA 的延长线上, EG 交 AB 于点 F,且∠BEF+∠ADC=180°,∠AFG与∠G相等吗 为什么
17.如图是一种可调节角度的躺椅及其简化的结构示意图,已知AB∥CD,O是AB 上一点,OE 与CD交于点G,OF 与CD 交于点D,DM∥OE,DM 与 AB 交于点N.当时,躺椅的舒适度最高,求此时 和∠MNB的度数.
18.如图,平面内的直线有相交和平行两种位置关系,
(1)如图 1,已知AB∥CD,求证:. ∠B+∠D;
(2)如图 2,已知 ∥求证:
19.如图,在 中, 点D,F在BC 边上,点E在AB 边上,点G在 AC 边上,EF 与GD的延长线交于点H ,
(1)判断EH和AD的位置关系,并说明理由;
(2)若 且 求的度数.
20.已知点 P 在直线CD 上, 请你说明:
参考答案
1. D 2. D 3. B 4. B 5. B 6. C 7. A
8. B 解析 :如图,将围巾展开,
则∠ADM=∠ADF,∠KCB=∠BCN,
设∠ABC = x,则∠DAB=x+8°,
因为CD∥AB,所以∠ADM=∠DAB=∠ADF=x+8°,∠KCB=∠CBN=∠BCN=x,
所以∠KCG=2x,∠FDM=2(x+8°),
因为 DF∥CG,所以∠FDC=∠KCG=2x,
因为∠FDC +∠FDM=180°,即 2x+2(x+8°)=180°,解得x=41°,
所以∠DAB+2∠ABC=(x+8°)+2x=131°.
9.36 10.α+β=θ 11.130 12.37°23′ 13.90
14.∠α+∠β-∠γ=180°
15.(1)180° (2)360° (3)(n-1)180°
16.解:∠AFG=∠G.
理由如下:
因为∠BEF+∠ADC=180°,∠BEF+∠GED=180°,所以∠GED=∠ADC.
所以AD∥GE,所以∠AFG=∠BAD,∠G=∠CAD,
因为 AD是∠BAC的平分线,所以∠BAD=∠CAD,
所以∠AFG=∠G.
17.解:因为 AB∥CD,∠ODC=32°,所以∠BOD=∠ODC=32°,
又因为OE⊥OF,所以∠EOF=90°,
所以∠AOE=180°-∠EOF-∠BOD=58°,
因为 DM∥OE,所以∠AND=∠AOE=58°,
所以∠MNB=∠AND=58°.
18.证明:(1)过点 P 作PE∥AB,如图1所示.
因为AB∥PE,AB∥CD,所以AB∥PE∥CD.
所以∠B=∠BPE,∠D=∠DPE,所以∠BPD=∠BPE+∠DPE=∠B+∠D;
(2)过点 P 作 如图2所示.
因为 ∥所以
因为 ∥所以
所以
所以 即
19.解:(1)EH∥AD,理由如下:
因为∠1=∠B,所以AB∥GD,所以∠2=∠BAD,
又因为∠2+∠3=180°,所以∠BAD+∠3=180°,所以 EH∥AD;
(2)由(1),得 AB∥GD,所以∠2=∠BAD,∠DGC=∠BAC,
因为∠DGC=60°,所以∠BAC=60°,
因为EH∥AD,所以∠2=∠H,所以∠H=∠BAD,
所以∠BAC=∠BAD+∠4=∠H+∠4=60°,
因为∠H-∠4=4°,所以∠H=32°.
20.解:因为∠BAP+∠APD=180°,所以AB∥CD,
所以∠BAP=∠APC,
又因为∠1=∠2,∠3=∠BAP-∠1,∠4=∠APC-∠2,所以∠3=∠4,
所以 AE∥PF,所以∠E=∠F.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
3 平行线的性质
第1课时 平行线的性质
1.如图, ∥点 E 在AC 的延长线上,下列结论一定成立的是( )
C.∠1=∠2 D.∠3=∠4
第1题图 第 2 题图
2.如图,将一块含有 角的直角三角板的顶点放在直尺的一边上.若∠1=42°,则∠2 的度数是 ( )
A.72° B.92° C.102° D.108°
3.如图,烧杯内液体表面AB 与烧杯下底部 CD 平行,光线 EF 从液体中射向空气时发生折射,光线变成 FH,点 G 在射线 EF 上. 已知 则∠GFH的度数为 ( )
A.20° B.40° C.60° D.80°
第3 题图 第 4 题图
4把一块直角三角板和一把直尺如图放置,若 ,则∠2 的度数等于( )
A.65° B.55° C.45°
5.一辆汽车在笔直的公路上行驶,两次拐弯后,还在原来的方向上平行前进,那么这两次拐弯的角度应是 ( )
A.第一次右拐 第二次左拐 B.第一次左拐 第二次右拐
C.第一次左拐 第二次左拐 D.第一次右拐 第二次右拐
6.如图,已知 ∥∠A=25°,∠CDE=135°,则. 的度数是 ( )
A.45° B.60° C.70° D.90°
第 6 题图 第7题图
7.如图,直线 MN∥EF,直角三角形 ABC 的直角顶点 A 在直线 EF上,边 AB 与MN 相交于点D,若∠ADM=123°,则∠FAC的度数为 ( )
A.33° B.43° C.57° D.67°
8.一条两边沿互相平行的围巾按图所示折叠,已知∠DAB-∠ABC=8°,且 DF∥CG,则 ∠DAB+2∠ABC= ( )
A.130° B.131° C.132° D. 133°
第 8题 第 9 题图
9.如图,直线 把三角尺的直角顶点放在直线 b上,若 则
10.我们规定车辆在转弯时的转弯角是车辆原行驶路线与转弯后路线所成的角的外角.如图一辆车在一段绕山公路行驶(沿箭头方向)时,在点 B,C和D 处的转弯角分别是α,β和θ,且 ∥DE,则α,β和θ之间的数量关系是__________.
11.如图,把一张长方形纸片 ABCD沿EF 折叠后,点 D,C 分别在点 M,N 的位置上,EM 与BC 的交点为G,若 则
12.已知直线 ∥将一块含角的直角三角板 ABC 按如图方式放置,若则 的度数为__________.
第12 题图 第 13 题图
13.幸福乡要修建一条灌溉水渠,如图,水渠从A 村沿北偏东 的方向到 B村,从 B 村沿北偏西 方向到C 村.若水渠从 C 村沿CD 方向修建可以保持与AB 的方向一致,则 的度数为_________°.
14.如图,已知 AB∥CD,则∠α,∠β,∠γ之间的关系为________.
15.如图,已知AB∥CD,试解决下列问题:
(1)∠1+∠2=____________;
(2)∠1+∠2+∠3=____________;
(3)试探究∠1+∠2+∠3+∠4+…+∠n=___________.
16.如图,已知 AD 是△ABC的角平分线,点D,E 在 BC 上,点 G 在 CA 的延长线上, EG 交 AB 于点 F,且∠BEF+∠ADC=180°,∠AFG与∠G相等吗 为什么
17.如图是一种可调节角度的躺椅及其简化的结构示意图,已知AB∥CD,O是AB 上一点,OE 与CD交于点G,OF 与CD 交于点D,DM∥OE,DM 与 AB 交于点N.当时,躺椅的舒适度最高,求此时 和∠MNB的度数.
18.如图,平面内的直线有相交和平行两种位置关系,
(1)如图 1,已知AB∥CD,求证:. ∠B+∠D;
(2)如图 2,已知 ∥求证:
19.如图,在 中, 点D,F在BC 边上,点E在AB 边上,点G在 AC 边上,EF 与GD的延长线交于点H ,
(1)判断EH和AD的位置关系,并说明理由;
(2)若 且 求的度数.
20.已知点 P 在直线CD 上, 请你说明:
参考答案
1. D 2. D 3. B 4. B 5. B 6. C 7. A
8. B 解析 :如图,将围巾展开,
则∠ADM=∠ADF,∠KCB=∠BCN,
设∠ABC = x,则∠DAB=x+8°,
因为CD∥AB,所以∠ADM=∠DAB=∠ADF=x+8°,∠KCB=∠CBN=∠BCN=x,
所以∠KCG=2x,∠FDM=2(x+8°),
因为 DF∥CG,所以∠FDC=∠KCG=2x,
因为∠FDC +∠FDM=180°,即 2x+2(x+8°)=180°,解得x=41°,
所以∠DAB+2∠ABC=(x+8°)+2x=131°.
9.36 10.α+β=θ 11.130 12.37°23′ 13.90
14.∠α+∠β-∠γ=180°
15.(1)180° (2)360° (3)(n-1)180°
16.解:∠AFG=∠G.
理由如下:
因为∠BEF+∠ADC=180°,∠BEF+∠GED=180°,所以∠GED=∠ADC.
所以AD∥GE,所以∠AFG=∠BAD,∠G=∠CAD,
因为 AD是∠BAC的平分线,所以∠BAD=∠CAD,
所以∠AFG=∠G.
17.解:因为 AB∥CD,∠ODC=32°,所以∠BOD=∠ODC=32°,
又因为OE⊥OF,所以∠EOF=90°,
所以∠AOE=180°-∠EOF-∠BOD=58°,
因为 DM∥OE,所以∠AND=∠AOE=58°,
所以∠MNB=∠AND=58°.
18.证明:(1)过点 P 作PE∥AB,如图1所示.
因为AB∥PE,AB∥CD,所以AB∥PE∥CD.
所以∠B=∠BPE,∠D=∠DPE,所以∠BPD=∠BPE+∠DPE=∠B+∠D;
(2)过点 P 作 如图2所示.
因为 ∥所以
因为 ∥所以
所以
所以 即
19.解:(1)EH∥AD,理由如下:
因为∠1=∠B,所以AB∥GD,所以∠2=∠BAD,
又因为∠2+∠3=180°,所以∠BAD+∠3=180°,所以 EH∥AD;
(2)由(1),得 AB∥GD,所以∠2=∠BAD,∠DGC=∠BAC,
因为∠DGC=60°,所以∠BAC=60°,
因为EH∥AD,所以∠2=∠H,所以∠H=∠BAD,
所以∠BAC=∠BAD+∠4=∠H+∠4=60°,
因为∠H-∠4=4°,所以∠H=32°.
20.解:因为∠BAP+∠APD=180°,所以AB∥CD,
所以∠BAP=∠APC,
又因为∠1=∠2,∠3=∠BAP-∠1,∠4=∠APC-∠2,所以∠3=∠4,
所以 AE∥PF,所以∠E=∠F.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
