09年新高考解析几何命题展望与复习建议
文档属性
| 名称 | 09年新高考解析几何命题展望与复习建议 |

|
|
| 格式 | rar | ||
| 文件大小 | 797.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-12 00:00:00 | ||
图片预览









文档简介
课件48张PPT。 突显理念 突出能力
09年新高考解析几何命题展望
与复习建议
一.回顾分析1。我省五年自主命题试题特点
2004:稳、实
2005:稳、实、活、蕴、亲
内容稳定、思维灵活、本质深刻
2006:重点突出,平稳前进
稳定有余,创新不足 ,难易极端
2007:稳定不固定;前进不急进;
简约不简单
2008: 题型稳定;重点突出;
简约新颖;难度上升
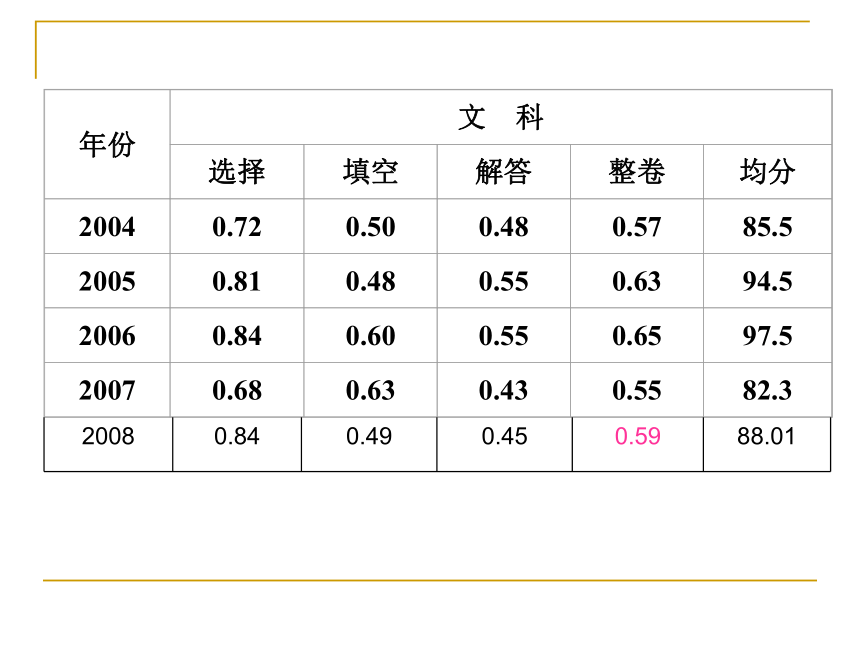
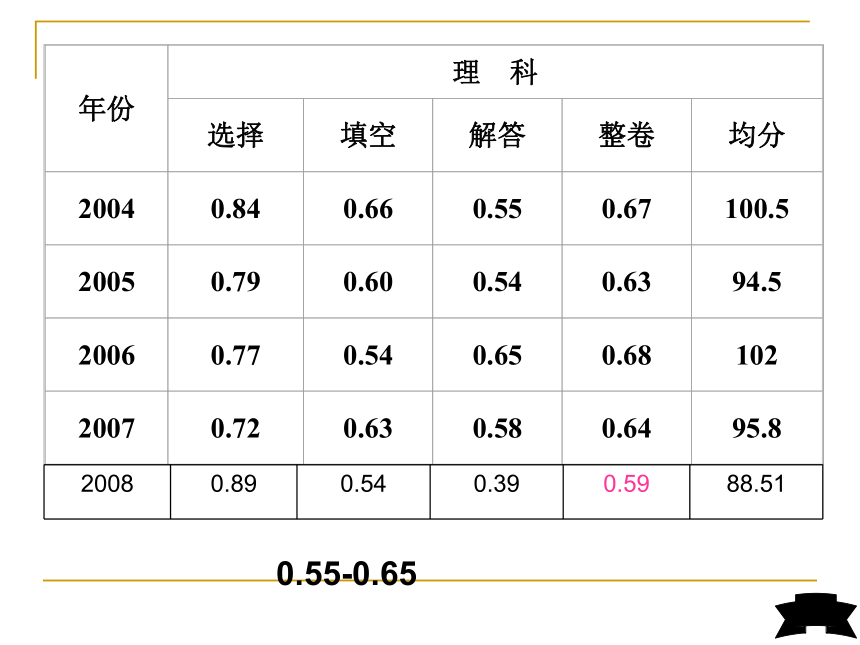
0.55-0.6508浙江高考数学试题难在何处?1.填空题的后三个题目成了“拦路虎.”2.解答题的“门槛”偏 高.3.解析几何解答题(第20题)成了不少数学
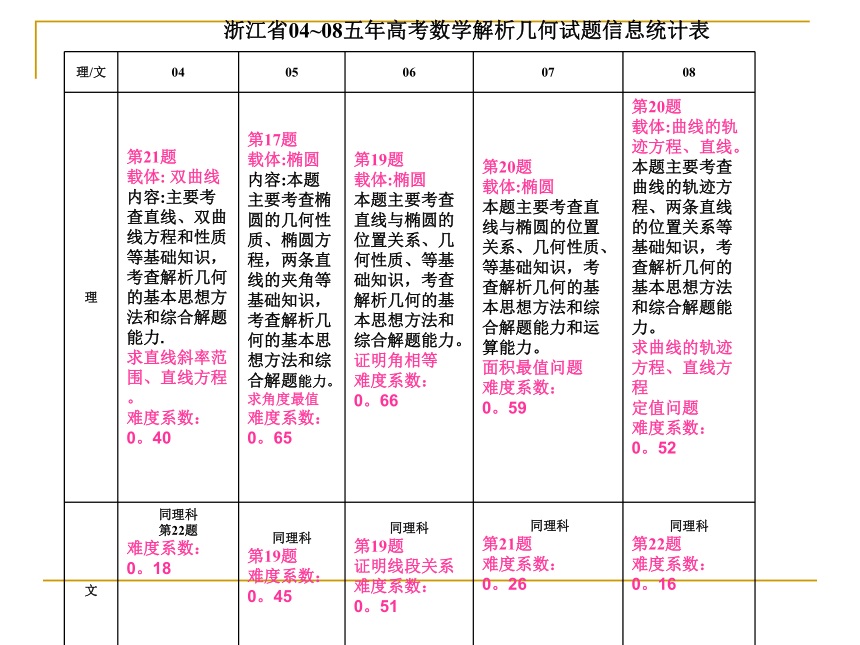
准高手的“滑铁卢”.4.压轴题成了“蜀道”,多数考生“难于上青天.”5.试卷的题量大,运算量也较大. 浙江省04~08五年高考数学解析几何试题信息统计表
五年特点(1)从整体来看:
模仿继承 注重传统
(2)从内容来看:
解析几何五年解答题分别是双曲线、抛
物线和椭圆,其中椭圆三年。
各种主要题型全面覆盖
(3)从思想方法来看:
五年都考查解析几何的基本思想方法及
综合解题能力和运算能力。
2。课改区试卷评述课改区解几试卷特点(1)从整体来看:
模仿继承 创新突破 注重本原
(2)从内容来看:
解析几何解答题载体是以直线与圆、抛
物线和椭圆为主,各种主要题型全面覆盖.
(3)从思想方法来看:
都考查解析几何的基本思想方法及
综合解题能力和运算能力。同时更加强调探究能力.
(4)广东和江苏难度降低,位置在大题居中间,不是起压轴题作用.
试题特点 1、立足基础 突出主干
2、紧贴课改 彰显理念 3、凸显新意 呈现亮点4、注重联系 加强综合 二.考试要求分析与展望1.考试说明 课程标准 学科指导意见考试说明
四、平面解析几何初步
(一)直线与方程
1.在平面直角坐标系中,结合具体图形,确定直线位置的几何要素。
2.理解直线的倾斜角和斜率的概念及相互间的关系,掌握过两点的直线斜率的计算公式。
3.能根据两条直线的斜率判定这两条直线平行或垂直。
4.掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系。
5.能用解方程组的方法求两直线的交点坐标。
6.掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
考试说明
四、(二)圆与方程
1.掌握确定圆的几何要素,掌握圆的标准方程与一般方程。
2.能根据给定直线、圆的方程,判断直线与圆的位置关系;能根据给定两个圆的方程,判断两圆的位置关系。
3.能用直线和圆的方程解决一些简单的问题。
4.初步了解用代数方法处理几何问题的思想。
(三)空间直角坐标系
1.了解空间直角坐标系,会用空间直角坐标表示点的位置。
2.了解空间两点间的距离公式。考试说明
十五、圆锥曲线与方程
(一)圆锥曲线
1.了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用。
2.掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质。
3.了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质。
4.能用坐标法解决简单的直线与椭圆、抛物线的位置关系等问题。
5.圆锥曲线的简单应用。
(二)曲线与方程
了解方程的曲线与曲线的方程的对应关系。现以“圆锥曲线与方程”为例加以解读(理科):对“知识要求”的三个层次:
2008年:对知识的要求依次是了解、理解和掌握、灵活和综合运用三个层次。
2009年:对知识的要求依次是了解、理解、掌握三个层次。
初步解读:对“知识要求”的层次进行了较大调整,增强了复习的可操作性。高考经验告诉我们,高考知识要求中的“了解”、“理解”和“掌握”三个层次,往往跟“不一定考”、“有可能考”、“要考的可能性很大”有些相匹配。
对“能力”的阐释:
2008年:能力是指思维能力、运算能力、空间想象能力、分析和解决问题的能力以及创新意识。
2009年:能力是指空间想像能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识。
初步解读:对“能力”的表述与新课程标准一致,它包括“五能力两意识”。解析几何是考查能力的一个传统载体。
(二) 考试要求分析2.样卷 教材五年高考试卷剖析参考试卷(样卷)
《理科(其中:考查内容中有*的是新知识考点;难度估计中有★★的为容易题、有★★★为中等题,有★★★★或★★★★★的为难题。)重点内容分布
由于椭圆、双曲线的准线概念已不再引入,涉及它们的许多相关知识已无法接触,因此圆和抛物线的教学地位将明显上升,而双曲线的教学要求则会相对降低;教材“导向”:
04~08年,特别08理科第20题(文科第22题)主要考查求曲线的轨迹方程、两条直线的位置关系等知识,考查解析几何的基本思想和综合解题能力。它关注解析几何的本质和数形结合的思想,尤其是第(Ⅱ)小题思路广、方法多、品质高,富有探究味,体现新课程理念,它对数学教学如何“摆脱题海”、关注数学本质起到了良好的导向作用。
命题展望:
(1)三种圆锥曲线的地位均衡性已经被打破,双曲线的地位明显下降,以它作为载体的解析几何大题的可能性已减少;
(2)解析几何大题的最大可能素材:
理科用坐标法解决直线与椭圆、抛物线的位置关系等问题;
文科用坐标法解决直线与抛物线的位置关系等问题.
(3) 双曲线的定义、几何图形和标准方程以及简单几何性质,方程的曲线与曲线的方程的对应关系等可能会在小题中加以考查;
(4) 把“了解圆锥曲线的简单应用和理解数形结合的思想”联系起来看,我们要关注应用性小题的可能性。
(5)我们要关注解析几何中的探究创新问题.
三.复习建议(一)抓准才能有效(二)抓实才能提高(三)抓活才能培养抓准——抓准《考试说明和要求》
领会《参考试卷》的内涵
不做无用功抓实—解析几何突出常规,重在落实基础,关注通性通法,注意平面几何的小技巧的应用.运算能力要加强训练,重视数学思想方法,提高基本技能。
(1)我们要总结解题的基本思想和方法,重点是有价值的常规方法的应用,特别要重视教科书中每章知识所给出的解决问题的核心方法。运用韦达定理的解题方法是解析几何中解决直线和圆锥曲线问题的核心方法,其解题步骤是“设”(点的坐标,直线、曲线方程)、“联”(联立方程组)、“消”(消去 得到一元二次方程)、“用”( 运用韦达定理、中点坐标公式、弦长公式等)、“判”( 运用判别式检验、求参数的值或缩小参数的取值范围)。凡是“点差法”能够解决的问题都可以用核心方法加以解决。每节课的设计紧紧围绕核心方法展开,知识重点要突出,学生才印象深刻。 (2)抓实重要专题
1。曲线方程的求法
2。中点、弦长、面积问题
3。最值与范围问题
4。向量与解析几何联系问题
5。函数、方程、导数、不等式、数列与解析几何联系问题 从07、08年的新课标试题看,一个显著特点是注重基础。从以往的高考经验看,解析几何是考生数学得分的主要标志之一,基本概念不清楚,基本运算不正确以及基本方法不熟练,这就要求我们在第二轮复习中仍然要重视基本概念、基础运算、突出基本方法、强调基本能力和素养.同时,夯实基础不等于对课本知识进行简单的重复再现;或机械地使用复习资料,没有效果的傻练。抓活——点燃学生思维火花,
培养学生探究能力.
重视探究能力和方法的训练,重视交汇综合。目前,我们都进入了高考第二轮复习
学生到底掌握了什么? 多少?
熟练程度如何?
老师需要做什么?
做为高三老师怎样引导学生复习才能
提高课堂效果呢? 一个课堂教学案例
例1.(江苏18)设平面直角坐标系中,设二次函数
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(Ⅰ)求实数b 的取值范围;
(Ⅱ)求圆C 的方程;
(Ⅲ)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.应让学生先动手解决,观察学生.
(Ⅰ)请一位同学板书解题过程(照抄于下):
解:由题意得Δ>0,解得b<1 .
评析:这是题意理解不清,思考不够深刻所致。
改进:由题意得抛物线与y轴交点是(0,b);
所以方程 =0 有两个不同的非零实根,
则 b≠0 且Δ>0,解得b<1 且b≠0.一个课堂教学案例
(Ⅱ)求圆C 的方程;(Ⅱ)请二位同学板书解题过程:
学生1:设所求圆的一般方程为
由方程令 =0 得 这 与 =0 是同一个方程,故D=2,F= .
令 =0 得 =0,此方程有一个根为b,代入得出E=―b―1.
所以圆C 的方程为 . 一个课堂教学案例学生2:设圆的一般方程为评析:(1)同是设为一般式,两种过程比较,要注意什么?
(2)是否可以利用标准式方程求解?
一个课堂教学案例 (Ⅱ)求圆C 的方程;
所以圆方程为学生3:由已知可以设圆方程为:只有放手让学生做题才能得到有效的教学 一个课堂教学案例
(Ⅲ)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.学生4:将圆方程化为以b为主元的方程就可以了。
评析:是否可以有其他方法?
学生5:从标准式方程可以观察出这两个定点。
评析 很好,其一般思想方法是什么?探究:是否存在实数b,使得△ABD为直角三角形?
还可以继续探究…利用数形结合、几何性质、分类讨论…我们还能找到可以进行探究、培养能力的素材,教师对数学的理解是发挥教师作用的基石。例2.(山东22) 如图,设抛物线方程为x2=2py(p>0),M为
直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
(Ⅰ)求证:A,M,B三点的横坐标成等差数列;
(Ⅱ)已知当M点的坐标为(2,-2p)时, ,求此时抛物线的方程;
(Ⅲ)是否存在点M,使得点C关于直线AB的对称点D在抛物线上,其中,点C 满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
我们可否探究:
若过此抛物线的焦点F作一直线与抛物线交于A、B两点,过这两点分别作抛物线的切线,
(1)求这两切线的交点M轨迹方程,并判断其逆命题是否成立?
(2)是否存在p,使得直线MA与MB相互垂直?
(3)当p=1时,是否存在常数λ,使等式 恒成立?
做了成千上万道数学题,学生(也包括我们数学教师)是否感悟到了存在于其中的数学本质,是否领会了数学概念、法则、结论的发展过程?解析几何的本质就是用代数的方法研究图形的几何性质,通过复习学生应该也必须领悟到其中的真缔。数学思想方法是数学知识在更高层次上的抽象和概括,是数学知识转化为能力的桥梁。课堂教学理应坚持以数学知识为载体,突出对数学思想方法的理解、掌握和运用。高三复习教学不应刻意追求特殊技巧,要在“通性、通法”上、培养能力上大做文章、做好文章。 因此,重视数学解题教学的研究、严格学生解题
的规范训练和能力训练就显得特别重要,我们要解决好解析几何中运算能力、基本方法的选择应用能力等一些“老大难”问题。课堂我们要想方设法、放开手脚让学生去思考,去表现,让学生去评判,让学生去纠正和体会,复习教学不要太多的题目数量,而要更多的思维含量。
这应该成为我们的教学共识! 以下练习供参考:
1.已知抛物线C的一个焦点为F(,0),对应于这个焦点的准线方程为x=-
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,
求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆(x-3)2+y2=2的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
2。已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
(I)求动点D的轨迹E的方程;
(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明. 3。已知半椭圆 与半椭圆 组成的曲线称为
“果圆”,其中 , 是对应的焦点。
(1)若三角形 是边长为1的等边三角形,求“果圆”的方程;
(2)若 ,求 的取值范围;
(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数 ,使得斜率为 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有的 值;若不存在,说明理由。(07上海)
个人想法
敬请指正
谢谢!
09年新高考解析几何命题展望
与复习建议
一.回顾分析1。我省五年自主命题试题特点
2004:稳、实
2005:稳、实、活、蕴、亲
内容稳定、思维灵活、本质深刻
2006:重点突出,平稳前进
稳定有余,创新不足 ,难易极端
2007:稳定不固定;前进不急进;
简约不简单
2008: 题型稳定;重点突出;
简约新颖;难度上升
0.55-0.6508浙江高考数学试题难在何处?1.填空题的后三个题目成了“拦路虎.”2.解答题的“门槛”偏 高.3.解析几何解答题(第20题)成了不少数学
准高手的“滑铁卢”.4.压轴题成了“蜀道”,多数考生“难于上青天.”5.试卷的题量大,运算量也较大. 浙江省04~08五年高考数学解析几何试题信息统计表
五年特点(1)从整体来看:
模仿继承 注重传统
(2)从内容来看:
解析几何五年解答题分别是双曲线、抛
物线和椭圆,其中椭圆三年。
各种主要题型全面覆盖
(3)从思想方法来看:
五年都考查解析几何的基本思想方法及
综合解题能力和运算能力。
2。课改区试卷评述课改区解几试卷特点(1)从整体来看:
模仿继承 创新突破 注重本原
(2)从内容来看:
解析几何解答题载体是以直线与圆、抛
物线和椭圆为主,各种主要题型全面覆盖.
(3)从思想方法来看:
都考查解析几何的基本思想方法及
综合解题能力和运算能力。同时更加强调探究能力.
(4)广东和江苏难度降低,位置在大题居中间,不是起压轴题作用.
试题特点 1、立足基础 突出主干
2、紧贴课改 彰显理念 3、凸显新意 呈现亮点4、注重联系 加强综合 二.考试要求分析与展望1.考试说明 课程标准 学科指导意见考试说明
四、平面解析几何初步
(一)直线与方程
1.在平面直角坐标系中,结合具体图形,确定直线位置的几何要素。
2.理解直线的倾斜角和斜率的概念及相互间的关系,掌握过两点的直线斜率的计算公式。
3.能根据两条直线的斜率判定这两条直线平行或垂直。
4.掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系。
5.能用解方程组的方法求两直线的交点坐标。
6.掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
考试说明
四、(二)圆与方程
1.掌握确定圆的几何要素,掌握圆的标准方程与一般方程。
2.能根据给定直线、圆的方程,判断直线与圆的位置关系;能根据给定两个圆的方程,判断两圆的位置关系。
3.能用直线和圆的方程解决一些简单的问题。
4.初步了解用代数方法处理几何问题的思想。
(三)空间直角坐标系
1.了解空间直角坐标系,会用空间直角坐标表示点的位置。
2.了解空间两点间的距离公式。考试说明
十五、圆锥曲线与方程
(一)圆锥曲线
1.了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用。
2.掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质。
3.了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质。
4.能用坐标法解决简单的直线与椭圆、抛物线的位置关系等问题。
5.圆锥曲线的简单应用。
(二)曲线与方程
了解方程的曲线与曲线的方程的对应关系。现以“圆锥曲线与方程”为例加以解读(理科):对“知识要求”的三个层次:
2008年:对知识的要求依次是了解、理解和掌握、灵活和综合运用三个层次。
2009年:对知识的要求依次是了解、理解、掌握三个层次。
初步解读:对“知识要求”的层次进行了较大调整,增强了复习的可操作性。高考经验告诉我们,高考知识要求中的“了解”、“理解”和“掌握”三个层次,往往跟“不一定考”、“有可能考”、“要考的可能性很大”有些相匹配。
对“能力”的阐释:
2008年:能力是指思维能力、运算能力、空间想象能力、分析和解决问题的能力以及创新意识。
2009年:能力是指空间想像能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识。
初步解读:对“能力”的表述与新课程标准一致,它包括“五能力两意识”。解析几何是考查能力的一个传统载体。
(二) 考试要求分析2.样卷 教材五年高考试卷剖析参考试卷(样卷)
《理科(其中:考查内容中有*的是新知识考点;难度估计中有★★的为容易题、有★★★为中等题,有★★★★或★★★★★的为难题。)重点内容分布
由于椭圆、双曲线的准线概念已不再引入,涉及它们的许多相关知识已无法接触,因此圆和抛物线的教学地位将明显上升,而双曲线的教学要求则会相对降低;教材“导向”:
04~08年,特别08理科第20题(文科第22题)主要考查求曲线的轨迹方程、两条直线的位置关系等知识,考查解析几何的基本思想和综合解题能力。它关注解析几何的本质和数形结合的思想,尤其是第(Ⅱ)小题思路广、方法多、品质高,富有探究味,体现新课程理念,它对数学教学如何“摆脱题海”、关注数学本质起到了良好的导向作用。
命题展望:
(1)三种圆锥曲线的地位均衡性已经被打破,双曲线的地位明显下降,以它作为载体的解析几何大题的可能性已减少;
(2)解析几何大题的最大可能素材:
理科用坐标法解决直线与椭圆、抛物线的位置关系等问题;
文科用坐标法解决直线与抛物线的位置关系等问题.
(3) 双曲线的定义、几何图形和标准方程以及简单几何性质,方程的曲线与曲线的方程的对应关系等可能会在小题中加以考查;
(4) 把“了解圆锥曲线的简单应用和理解数形结合的思想”联系起来看,我们要关注应用性小题的可能性。
(5)我们要关注解析几何中的探究创新问题.
三.复习建议(一)抓准才能有效(二)抓实才能提高(三)抓活才能培养抓准——抓准《考试说明和要求》
领会《参考试卷》的内涵
不做无用功抓实—解析几何突出常规,重在落实基础,关注通性通法,注意平面几何的小技巧的应用.运算能力要加强训练,重视数学思想方法,提高基本技能。
(1)我们要总结解题的基本思想和方法,重点是有价值的常规方法的应用,特别要重视教科书中每章知识所给出的解决问题的核心方法。运用韦达定理的解题方法是解析几何中解决直线和圆锥曲线问题的核心方法,其解题步骤是“设”(点的坐标,直线、曲线方程)、“联”(联立方程组)、“消”(消去 得到一元二次方程)、“用”( 运用韦达定理、中点坐标公式、弦长公式等)、“判”( 运用判别式检验、求参数的值或缩小参数的取值范围)。凡是“点差法”能够解决的问题都可以用核心方法加以解决。每节课的设计紧紧围绕核心方法展开,知识重点要突出,学生才印象深刻。 (2)抓实重要专题
1。曲线方程的求法
2。中点、弦长、面积问题
3。最值与范围问题
4。向量与解析几何联系问题
5。函数、方程、导数、不等式、数列与解析几何联系问题 从07、08年的新课标试题看,一个显著特点是注重基础。从以往的高考经验看,解析几何是考生数学得分的主要标志之一,基本概念不清楚,基本运算不正确以及基本方法不熟练,这就要求我们在第二轮复习中仍然要重视基本概念、基础运算、突出基本方法、强调基本能力和素养.同时,夯实基础不等于对课本知识进行简单的重复再现;或机械地使用复习资料,没有效果的傻练。抓活——点燃学生思维火花,
培养学生探究能力.
重视探究能力和方法的训练,重视交汇综合。目前,我们都进入了高考第二轮复习
学生到底掌握了什么? 多少?
熟练程度如何?
老师需要做什么?
做为高三老师怎样引导学生复习才能
提高课堂效果呢? 一个课堂教学案例
例1.(江苏18)设平面直角坐标系中,设二次函数
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(Ⅰ)求实数b 的取值范围;
(Ⅱ)求圆C 的方程;
(Ⅲ)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.应让学生先动手解决,观察学生.
(Ⅰ)请一位同学板书解题过程(照抄于下):
解:由题意得Δ>0,解得b<1 .
评析:这是题意理解不清,思考不够深刻所致。
改进:由题意得抛物线与y轴交点是(0,b);
所以方程 =0 有两个不同的非零实根,
则 b≠0 且Δ>0,解得b<1 且b≠0.一个课堂教学案例
(Ⅱ)求圆C 的方程;(Ⅱ)请二位同学板书解题过程:
学生1:设所求圆的一般方程为
由方程令 =0 得 这 与 =0 是同一个方程,故D=2,F= .
令 =0 得 =0,此方程有一个根为b,代入得出E=―b―1.
所以圆C 的方程为 . 一个课堂教学案例学生2:设圆的一般方程为评析:(1)同是设为一般式,两种过程比较,要注意什么?
(2)是否可以利用标准式方程求解?
一个课堂教学案例 (Ⅱ)求圆C 的方程;
所以圆方程为学生3:由已知可以设圆方程为:只有放手让学生做题才能得到有效的教学 一个课堂教学案例
(Ⅲ)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.学生4:将圆方程化为以b为主元的方程就可以了。
评析:是否可以有其他方法?
学生5:从标准式方程可以观察出这两个定点。
评析 很好,其一般思想方法是什么?探究:是否存在实数b,使得△ABD为直角三角形?
还可以继续探究…利用数形结合、几何性质、分类讨论…我们还能找到可以进行探究、培养能力的素材,教师对数学的理解是发挥教师作用的基石。例2.(山东22) 如图,设抛物线方程为x2=2py(p>0),M为
直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
(Ⅰ)求证:A,M,B三点的横坐标成等差数列;
(Ⅱ)已知当M点的坐标为(2,-2p)时, ,求此时抛物线的方程;
(Ⅲ)是否存在点M,使得点C关于直线AB的对称点D在抛物线上,其中,点C 满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
我们可否探究:
若过此抛物线的焦点F作一直线与抛物线交于A、B两点,过这两点分别作抛物线的切线,
(1)求这两切线的交点M轨迹方程,并判断其逆命题是否成立?
(2)是否存在p,使得直线MA与MB相互垂直?
(3)当p=1时,是否存在常数λ,使等式 恒成立?
做了成千上万道数学题,学生(也包括我们数学教师)是否感悟到了存在于其中的数学本质,是否领会了数学概念、法则、结论的发展过程?解析几何的本质就是用代数的方法研究图形的几何性质,通过复习学生应该也必须领悟到其中的真缔。数学思想方法是数学知识在更高层次上的抽象和概括,是数学知识转化为能力的桥梁。课堂教学理应坚持以数学知识为载体,突出对数学思想方法的理解、掌握和运用。高三复习教学不应刻意追求特殊技巧,要在“通性、通法”上、培养能力上大做文章、做好文章。 因此,重视数学解题教学的研究、严格学生解题
的规范训练和能力训练就显得特别重要,我们要解决好解析几何中运算能力、基本方法的选择应用能力等一些“老大难”问题。课堂我们要想方设法、放开手脚让学生去思考,去表现,让学生去评判,让学生去纠正和体会,复习教学不要太多的题目数量,而要更多的思维含量。
这应该成为我们的教学共识! 以下练习供参考:
1.已知抛物线C的一个焦点为F(,0),对应于这个焦点的准线方程为x=-
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,
求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆(x-3)2+y2=2的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
2。已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
(I)求动点D的轨迹E的方程;
(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明. 3。已知半椭圆 与半椭圆 组成的曲线称为
“果圆”,其中 , 是对应的焦点。
(1)若三角形 是边长为1的等边三角形,求“果圆”的方程;
(2)若 ,求 的取值范围;
(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数 ,使得斜率为 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有的 值;若不存在,说明理由。(07上海)
个人想法
敬请指正
谢谢!
同课章节目录
