北京市中国人民大学附属中学2023-2024学年高一上学期期末数学试题(含答案)
文档属性
| 名称 | 北京市中国人民大学附属中学2023-2024学年高一上学期期末数学试题(含答案) | 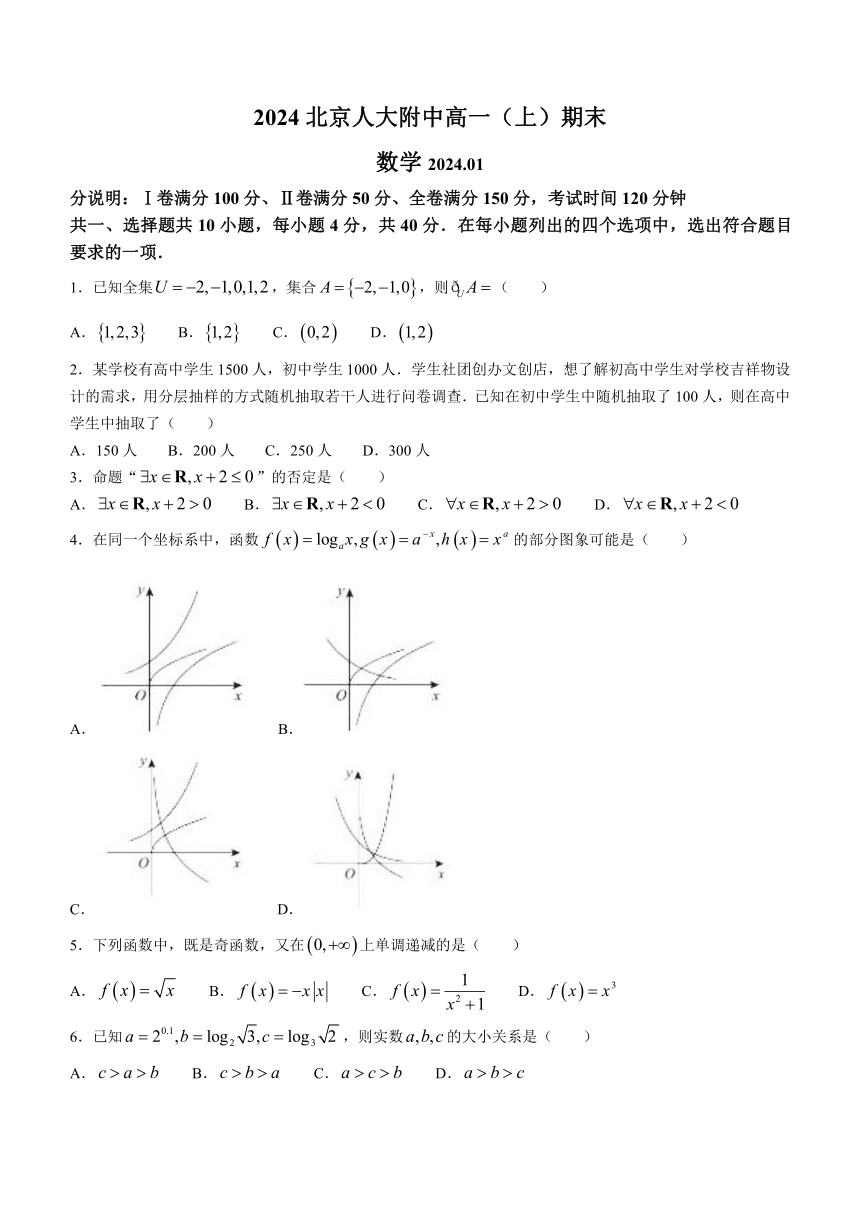 | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-15 09:57:57 | ||
图片预览





文档简介
2024北京人大附中高一(上)期末
数学2024.01
分说明:Ⅰ卷满分100分、Ⅱ卷满分50分、全卷满分150分,考试时间120分钟
共一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知全集,集合,则( )
A. B. C. D.
2.某学校有高中学生1500人,初中学生1000人.学生社团创办文创店,想了解初高中学生对学校吉祥物设计的需求,用分层抽样的方式随机抽取若干人进行问卷调查.已知在初中学生中随机抽取了100人,则在高中学生中抽取了( )
A.150人 B.200人 C.250人 D.300人
3.命题“”的否定是( )
A. B. C. D.
4.在同一个坐标系中,函数的部分图象可能是( )
A. B.
C. D.
5.下列函数中,既是奇函数,又在上单调递减的是( )
A. B. C. D.
6.已知,则实数的大小关系是( )
A. B. C. D.
7.已知函数,则“”是“为奇函数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
8.已知函数,则不等式的解集为( )
A. B. C. D.
9.科赫(Koch)曲线是几何中最简单的分形.科赫曲线的产生方式如下:如图,将一条线段三等分后,以中间一段为边作正三角形并去掉原线段生成1级科赫曲线“”,将1级科赫曲线上每一线段重复上述步骤得到2级科赫曲线,同理可得3级科赫曲线......在分形中,一个图形通常由个与它的上一级图形相似,且相似比为的部分组成.若,则称为该图形的分形维数.那么科赫曲线的分形维数是( )
A. B. C.1 D.
10.已知函数,若存在非零实数,使得成立,则实数的取值范围是( )
A. B. C. D.
二、填空题共5小题,每小题4分,共20分.
11.函数的定义域是_________________.
12.农科院作物所为了解某种农作物的幼苗质量,分别从该农作物在甲、乙两个不同环境下培育的幼苗中各随机抽取了15株幼苗进行检测,量出它们的高度如下图(单位:):
记该样本中甲、乙两种环境下幼苗高度的中位数分别为,则_________________;
若以样本估计总体,记甲、乙两种环境下幼苗高度的标准差分别为,则_________________(用“<,>或=”连接).
13.已知函数没有零点,则的一个取值为_________________;的取值范围是_________________.
14.已知函数则的单调递增区间为_________________;满足的整数解的个数为_________________.(参考数据:)
15.共享单车已经逐渐成为人们在日常生活中必不可少的交通工具.通过调查发现人们在单车选择时,可以使用“Tullock竞争函数”进行近似估计,其解析式为(其中参数表示市场外部性强度,越大表示外部性越强).给出下列四个结论:
①过定点;
②在上单调递增;
③关于对称;
④取定,外部性强度越大,越小.
其中所有正确结论的序号是_________________.
三、解答题共4小题,共40分.解答应写出文字说明,演算步骤或证明过程.
16.国务院正式公布的《第一批全国重点文物保护单位名单》中把重点文物保护单位(下述简称为“第一批文保单位”)分为六大类.其中“:革命遗址及革命纪念建筑物”、“:石窟寺”、“:古建筑及历史纪念建筑物”、“:石刻及其他”、“:古遗址”、“:古墓葬”.北京的18个“第一批文保单位”所在区分布如下表:
行政区 门类 个数
东城区 A:革命遗址及革命纪念建筑物 3
C:古建筑及历史纪念建筑物 5
西城区 C:古建筑及历史纪念建筑物 2
丰台区 A:革命遗址及革命纪念建筑物 1
海淀区 C:古建筑及历史纪念建筑物 2
房山区 C:古建筑及历史纪念建筑物 1
E:古遗址 1
昌平区 C:古建筑及历史纪念建筑物 1
F:古墓葬 1
延庆区 C:古建筑及历史纪念建筑物 1
(1)某个研学小组随机选择北京市“第一批文保单位”中的一个进行参观,求选中的参观单位恰好为“C:古建筑及历史纪念建筑物”的概率;
(2)小王同学随机选择北京市“第一批文保单位”中的“A:革命遗址及革命纪念建筑物”中的一个进行参观;小张同学随机选择北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中的一个进行参观.两人选择参观单位互不影响,求两人选择的参观单位恰好在同一个区的概率;
(3)现在拟从北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中随机抽取2个单位进行常规检查.记抽到海淀区的概率为,抽不到海淀区的概率记为,试判断和的大小(直接写出结论).
17.已知集合.
(1)求;
(2)记关于的不等式的解集为,若,求实数的取值范围.
18.已知函数.请从条件①、条件②这两个条件中选择一个作为已知,解答下面的问题.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答记分.
(1)求实数的值;
(2)设函数,判断函数在区间上的单调性,并给出证明;
(3)设函数,指出函数在区间上的零点个数,并说明理由.
19.已知函数的定义域均为,给出下面两个定义:
①若存在唯一的,使得,则称与关于唯一交换;
②若对任意的,均有,则称与关于任意交换.
(1)请判断函数与关于是唯一交换还是任意交换,并说明理由;
(2)设,若存在函数,使得与关于任意交换,求的值;
(3)在(2)的条件下,若与关于唯一交换,求的值.
Ⅱ卷
20.从定义域及值域均为的函数中随机选一个记为,则的概率为( )
A. B. C. D.
21.为( )
A.空集 B.元素个数不超过10的非空集 C.元素个数超过10的有限集 D.无限集
22.已知函数的单调递增区间是,单调递减区间是的零点个数为( )
A.1 B.2 C.3 D.4
23.若,则( )
A. B. C. D.
24.在企业生产经营过程中,柯布-道格拉斯生产函数有着广泛的应用,这是双自变量的函数,其表达式为:,其中自变量分别表示生产过程中劳动要素和资本要素的投入,函数值表示产量,常数是代表生产技术水平的参数,常数分别表示劳动和资本的产出弹性系数.在产量不变的情况下,点组合构成一条曲线,称为等效产出曲线.如图,某企业时的等效产出曲线分别与过原点的射线交于点,若,则约为( )
参考数据:
A.3.2 B.3.4 C.3.6 D.3.8
二、填空题(本大题共5小题,每小题6分,共30分.请将结果填在答题纸上的相应位置.)
25.已知.若,则实数_________________;若的图像关于原点对称,则实数_________________.
26.已知,其中.若,则的取值范围是_________________;若,则的取值范围是_________________.
27.为研究拇指指纹规律,人大附中生物社团随机抽样调查了500名北京市民的左右手拇指指纹,各种纹形出现次数的统计结果如表所示.①从左右手拇指纹形同为“As”或同为“Wr”的样本中,随机抽2人,这2人纹形不同的概率是②随机调查3名北京市民,其中1人左右手拇指指纹都是“Lu,Lr”,另外2人左手拇指指纹都是“Ws”,右手拇指指纹都不是“Ws”的概率是_________.
纹形 拇指
左手 右手 左右手纹形相同
As 20 2 2
Lu,Lr 279 304 250
Wr 3 6 2
Wc 32 27 10
Wt 30 28 9
Ws 59 79 34
Wd 65 37 18
Wp 12 17 8
总人数 500 500 333
28.已知函数的定义域为,若对任意的正实数,函数在上单调递增,则称函数具有性质,给出下列四个结论:
①在上单调递增,则具有性质;
②具有性质不具有性质;
③具有性质不具有性质;
④若函数具有性质,且,则.
其中所有正确结论的序号是_________________.
29.零件分别先在机器上加工,然后在机器上加工,加工所需时间(单位:分钟)如表所示.
①若加工顺序为,则加工完所有零件所需时间最少为分钟;
②改变这5个零件的加工顺序,可以使得加工完所有零件所需时间更少,所需时间最少为_________________分钟,共有_________________种排序方法使得所需时间最少.
机床 零件
1 5
8 3
3 9
4 5
7 6
参考答案
Ⅰ卷
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.【答案】B
【分析】根据补集概念求解出结果.
【详解】因为,
所以,
故选:B.
2.【答案】A
【分析】根据各层的抽样比相同求解出结果.
【详解】因为初中学生1000人抽取了100人,所以抽样比为,
所以高中生抽取人,
故选:A.
3.【答案】C
【分析】根据特称命题的否定是全称命题分析判断.
【详解】由题意可知:命题“”的否定是“”.
故选:C.
4.【答案】C
【分析】先根据的单调性相反排除AD,然后根据幂函数图象判断出的范围,由此可知正确图象.
【详解】因为在同一坐标系中,
所以的单调性一定相反,且图象均不过原点,故排除AD;
在BC选项中,过原点的图象为幂函数的图象,由图象可知,
所以单调递减,单调递增,故排除B,
故选:C.
5.【答案】B
【分析】利用定义判断函数的奇偶性可对A、C判断;利用函数奇偶性的判断并结合函数单调性可对B、D判断.
【详解】对A、C:由,定义域为,所以不是奇函数,故A错误;
定义域为,所以是偶函数,故C错误;
对B、D:,定义域为,所以为奇函数,当时,,且在上单调递减,故B正确;
,定义域为,且,所以为奇函数,且在定义域上为增函数,故D错误;
故选:B.
6.【答案】D
【分析】根据题意结合指、对数函数单调性运算求解.
【详解】因为,
由在上单调递增,可得,即;
由在内单调递增,可得,即;
由在内单调递增,可得,即;
综上所述:.
故选:D.
7.【答案】C
【分析】根据“”与“为奇函数”互相推出的情况判断属于何种条件.
【详解】当时,,定义域为且关于原点对称,
所以,
所以为奇函数;
当为奇函数时,显然定义域为且关于原点对称,所以,
所以,
所以,
由上可知,“”是“为奇函数”的充要条件,
故选:C.
8.【答案】B
第8页/共18页
【分析】先求出的定义域,然后分析的单调性,再根据求解出不等式解集.
【详解】的定义域为,
因为均在上单调递增,
所以在上单调递增,
又因为,所以,
所以不等式解集为,
故选:B.
9.【答案】D
【分析】根据题意得出Koch曲线是由把全体缩小的4个相似图形构成的,再根据题设条件即可得出结果.
【详解】由题意Koch曲线是由把全体缩小的4个相似图形构成的,
因为,即,则,
所以分形维数是.
故选:D.
10.【答案】D
【分析】利用赋值和排除法可得结果
【详解】取,则,
若,则,由,得,
解得,符合条件,排除选项A、C,
取,则,
若时,,由,得,
解得,或,都不符合条件,
若,即,由,
得,即,不符合条件,
若,即,由,
得,解得,或,都不符合条件,
综上,,排除B,选D
故选:D.
二、填空题共5小题,每小题4分,共20分.
11.【答案】
【分析】利用真数大于零列不等式求解即可.
【详解】要使函数有意义,
则,解得,
即函数的定义域是,
故答案为:.
【点睛】本题主要考查对数型复合函数的定义域,属于基础题.
12.【答案】①3 ②>
【分析】空①根据题意分别求出甲乙环境下的15个高度数据,从而求出中位数,即可求解;空②利用标准差公式分别求出,从而求解.
【详解】对空①:由题意得甲环境的幼苗高度为: 31,32,33,33,35,43,44,45,49,55,57,58,59,63,65,其中位数,
乙环境的幼苗高度为: 37,43,44,45,45,47,48,48,49,52,54,54,55,58,60,其中位数,所以;
对空②:甲环境下的幼苗平均高度为:
所以:
甲环境下的幼苗平均高度为:
所以
所以.
故答案为:3;>.
13.【答案】
①0 (即可) ②
【分析】根据题意分析可知函数没有零点,等价于与没有交点,结合对勾函数图象分析求解.
【详解】令,则,
若函数没有零点,等价于与没有交点,
作出的图象,如图所示:
由图象可知:若与没有交点,则,
故答案为:0即可);.
14.【答案】① ②215
【分析】第一个空,作出的图象,由图可知的单调递增区间;第二个空,分和两种情况解不等式.
【详解】作出的图象,由图可知,的单调递增区间为,
当时,,解得,即,
所以,
当时,,解得,
故满足的整数解的个数为215.
故答案为:;215.
15.【答案】①②
【分析】对于①令即可求得定点可判断①的正误;对于②对求导,判断导函数在时的正负即可判断②的正误;对于③由②即可判断正误;对于④以为自变量构造新函数,求导,判断单调性即可判断正误.
【详解】对于①,在中,令,则,过定点,故①正确;
对于②,,当,则为单调递增,故②正确;
对于③,由②知为单调递增,故不存在对称性,故③错误;
对于④,以为自变量,设为,则,
,故的正负取决于,
当,即时,,随着的增大,减小;
当,即时,,随着的增大,增大,故④错误.
故答案为:①②.
三、解答题共4小题,共40分.解答应写出文字说明,演算步骤或证明过程.
16.【答案】(1) (2) (3)
【分析】(1)由题意知总样本数为18,C:古建筑及历史纪念建筑物共有12,利用古典概率从而求解.
(2)由题意可知小王参观A:革命遗址及革命纪念建筑物与小张参观C:古建筑及历史纪念建筑物在同一个区的只有东城区,然后分别求出他们参观东城区的概率,从而求解.
(3)利用分类讨论求出相应的抽到海淀区的概率和抽不到海淀区的概率,从而求解.
【小问1详解】
设选中参观单位恰好为“C:古建筑及历史纪念建筑物”为事件A,
由题意知总共有18,“C:古建筑及历史纪念建筑物”有12,
所以.
【小问2详解】
设两人选择的参观单位恰好在同一个区为事件,由题意可知小王参观:革命遗址及革命纪念建筑物与小张参观:古建筑及历史纪念建筑物在同一个区的只有东城区,
所以小王参观东城区景区的概率为,小张参观东城区景区的概率为,
所以.
【小问3详解】
当抽到的2个都是海淀区的概率为,
当抽到的2个中有1个是海淀区的概率为,
所以,
所以.
17.【答案】(1)
(2)
【分析】(1)先求解出一元二次不等式、绝对值不等式的解集为集合,然后根据并集概念求解出,再根据交集和补集概念求解出;
(2)根据不等式先求解出,然后根据列出关于的不等式组,由此求解出结果.
【小问1详解】
因为,解得,所以,
又因为,解得或,所以,
所以;
又因为,
所以.
【小问2详解】
因为,
所以,
若,则,解得,
所以的取值范围是.
18.【答案】(1)答案见解析
(2)在区间上单调递减,证明见解析
(3)在内有且仅有一个零点,理由见解析
【分析】(1)根据题意结合奇偶性的定义分析求解;
(2)根据单调性的定义分析证明;
(3)根据题意结合单调性以及奇偶性的性质判断在区间上的单调性,再结合零点存在性定理分析判断.
【小问1详解】
令,解得,所以函数的定义域为,
若选①:因为,即为奇函数,
则,
整理得,
注意到对任意上式均成立,可得,解得;
若选②:因为,即为偶函数,
则,
整理得,
注意到对任意上式均成立,可得,解得.
【小问2详解】
若选①:则,可得,
可知函数在区间上单调递减,证明如下:
对任意,且,
则,
因为,则,
可得,即,
所以函数在区间上单调递减;
若选②:则,可得,
可知函数在区间上单调递减,证明如下:
对任意,且,
则,
因为,则,
可得,即,
所以函数在区间上单调递减.
【小问3详解】
若选①:则,则,
由(2)可知在内单调递减,且在定义域内单调递增,
可知在内单调递减,
又因为为奇函数,则在内单调递减,
且在内单调递减,可知在内单调递减,
结合,
可知在内有且仅有一个零点;
若选②:则,则,
由(2)可知在内单调递减,且在定义域内单调递增,
可知在内单调递减,
又因为为偶函数,则在内单调递增,
且在内单调递增,可知在内单调递增,
结合,
可知在内有且仅有一个零点.
19.【答案】(1)唯一交换,理由见解析
(2) (3)
【分析】(1)根据方程解的情况判断即可;
(2)根据“对任意的成立”得到关于的方程,然后设出的解析式,根据方程左右两边对应项相同求解出的值;
(3)根据条件通过分离参数将问题转化为“存在唯一实数,使得”,然后分析的奇偶性,从而确定出,由此可求的值.
【小问1详解】
与关于是唯一交换,理由如下:
因为,
令,所以,解得,
所以有唯一解,
所以与关于是唯一交换.
【小问2详解】
由题意可知,对任意的成立,
即对任意的;
考虑到等式左右两边最高次和最高次项的系数相等,不妨设,
所以,
所以,
所以,所以,即可取,
经检验满足要求,
综上所述,.
【小问3详解】
当时,,
因为与关于唯一交换,
所以存在唯一实数,使得,
即存在唯一实数,使得,
即存在唯一实数,使得;
令,且定义域均为,
又
,
所以都是偶函数,所以为偶函数,
因此,若存在唯一实数使得,只能是,
所以,
综上所述,的取值为.
【点睛】关键点点睛:本题考查函数的新定义,涉及方程解以及函数奇偶性等相关问题,对学生的理解与计算能力要求较高,难度较大.“新定义”题型的关键是根据新定义的概念、新公式、新定理、新法则、新运算去解决问题,本题第二问可以从方程左右两边对应相等入手,第三问则可以从函数的奇偶性入手进行分析.
Ⅱ卷
一、选择题(共5小题,每小题5分,共25分)
20.B 21.B 22.C 23.D 24.D
二、填空题(共5小题,每小题5分,共25分)
25.2; 26.;
27.; 28.②④
29.32;29;7
数学2024.01
分说明:Ⅰ卷满分100分、Ⅱ卷满分50分、全卷满分150分,考试时间120分钟
共一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知全集,集合,则( )
A. B. C. D.
2.某学校有高中学生1500人,初中学生1000人.学生社团创办文创店,想了解初高中学生对学校吉祥物设计的需求,用分层抽样的方式随机抽取若干人进行问卷调查.已知在初中学生中随机抽取了100人,则在高中学生中抽取了( )
A.150人 B.200人 C.250人 D.300人
3.命题“”的否定是( )
A. B. C. D.
4.在同一个坐标系中,函数的部分图象可能是( )
A. B.
C. D.
5.下列函数中,既是奇函数,又在上单调递减的是( )
A. B. C. D.
6.已知,则实数的大小关系是( )
A. B. C. D.
7.已知函数,则“”是“为奇函数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
8.已知函数,则不等式的解集为( )
A. B. C. D.
9.科赫(Koch)曲线是几何中最简单的分形.科赫曲线的产生方式如下:如图,将一条线段三等分后,以中间一段为边作正三角形并去掉原线段生成1级科赫曲线“”,将1级科赫曲线上每一线段重复上述步骤得到2级科赫曲线,同理可得3级科赫曲线......在分形中,一个图形通常由个与它的上一级图形相似,且相似比为的部分组成.若,则称为该图形的分形维数.那么科赫曲线的分形维数是( )
A. B. C.1 D.
10.已知函数,若存在非零实数,使得成立,则实数的取值范围是( )
A. B. C. D.
二、填空题共5小题,每小题4分,共20分.
11.函数的定义域是_________________.
12.农科院作物所为了解某种农作物的幼苗质量,分别从该农作物在甲、乙两个不同环境下培育的幼苗中各随机抽取了15株幼苗进行检测,量出它们的高度如下图(单位:):
记该样本中甲、乙两种环境下幼苗高度的中位数分别为,则_________________;
若以样本估计总体,记甲、乙两种环境下幼苗高度的标准差分别为,则_________________(用“<,>或=”连接).
13.已知函数没有零点,则的一个取值为_________________;的取值范围是_________________.
14.已知函数则的单调递增区间为_________________;满足的整数解的个数为_________________.(参考数据:)
15.共享单车已经逐渐成为人们在日常生活中必不可少的交通工具.通过调查发现人们在单车选择时,可以使用“Tullock竞争函数”进行近似估计,其解析式为(其中参数表示市场外部性强度,越大表示外部性越强).给出下列四个结论:
①过定点;
②在上单调递增;
③关于对称;
④取定,外部性强度越大,越小.
其中所有正确结论的序号是_________________.
三、解答题共4小题,共40分.解答应写出文字说明,演算步骤或证明过程.
16.国务院正式公布的《第一批全国重点文物保护单位名单》中把重点文物保护单位(下述简称为“第一批文保单位”)分为六大类.其中“:革命遗址及革命纪念建筑物”、“:石窟寺”、“:古建筑及历史纪念建筑物”、“:石刻及其他”、“:古遗址”、“:古墓葬”.北京的18个“第一批文保单位”所在区分布如下表:
行政区 门类 个数
东城区 A:革命遗址及革命纪念建筑物 3
C:古建筑及历史纪念建筑物 5
西城区 C:古建筑及历史纪念建筑物 2
丰台区 A:革命遗址及革命纪念建筑物 1
海淀区 C:古建筑及历史纪念建筑物 2
房山区 C:古建筑及历史纪念建筑物 1
E:古遗址 1
昌平区 C:古建筑及历史纪念建筑物 1
F:古墓葬 1
延庆区 C:古建筑及历史纪念建筑物 1
(1)某个研学小组随机选择北京市“第一批文保单位”中的一个进行参观,求选中的参观单位恰好为“C:古建筑及历史纪念建筑物”的概率;
(2)小王同学随机选择北京市“第一批文保单位”中的“A:革命遗址及革命纪念建筑物”中的一个进行参观;小张同学随机选择北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中的一个进行参观.两人选择参观单位互不影响,求两人选择的参观单位恰好在同一个区的概率;
(3)现在拟从北京市“第一批文保单位”中的“C:古建筑及历史纪念建筑物”中随机抽取2个单位进行常规检查.记抽到海淀区的概率为,抽不到海淀区的概率记为,试判断和的大小(直接写出结论).
17.已知集合.
(1)求;
(2)记关于的不等式的解集为,若,求实数的取值范围.
18.已知函数.请从条件①、条件②这两个条件中选择一个作为已知,解答下面的问题.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答记分.
(1)求实数的值;
(2)设函数,判断函数在区间上的单调性,并给出证明;
(3)设函数,指出函数在区间上的零点个数,并说明理由.
19.已知函数的定义域均为,给出下面两个定义:
①若存在唯一的,使得,则称与关于唯一交换;
②若对任意的,均有,则称与关于任意交换.
(1)请判断函数与关于是唯一交换还是任意交换,并说明理由;
(2)设,若存在函数,使得与关于任意交换,求的值;
(3)在(2)的条件下,若与关于唯一交换,求的值.
Ⅱ卷
20.从定义域及值域均为的函数中随机选一个记为,则的概率为( )
A. B. C. D.
21.为( )
A.空集 B.元素个数不超过10的非空集 C.元素个数超过10的有限集 D.无限集
22.已知函数的单调递增区间是,单调递减区间是的零点个数为( )
A.1 B.2 C.3 D.4
23.若,则( )
A. B. C. D.
24.在企业生产经营过程中,柯布-道格拉斯生产函数有着广泛的应用,这是双自变量的函数,其表达式为:,其中自变量分别表示生产过程中劳动要素和资本要素的投入,函数值表示产量,常数是代表生产技术水平的参数,常数分别表示劳动和资本的产出弹性系数.在产量不变的情况下,点组合构成一条曲线,称为等效产出曲线.如图,某企业时的等效产出曲线分别与过原点的射线交于点,若,则约为( )
参考数据:
A.3.2 B.3.4 C.3.6 D.3.8
二、填空题(本大题共5小题,每小题6分,共30分.请将结果填在答题纸上的相应位置.)
25.已知.若,则实数_________________;若的图像关于原点对称,则实数_________________.
26.已知,其中.若,则的取值范围是_________________;若,则的取值范围是_________________.
27.为研究拇指指纹规律,人大附中生物社团随机抽样调查了500名北京市民的左右手拇指指纹,各种纹形出现次数的统计结果如表所示.①从左右手拇指纹形同为“As”或同为“Wr”的样本中,随机抽2人,这2人纹形不同的概率是②随机调查3名北京市民,其中1人左右手拇指指纹都是“Lu,Lr”,另外2人左手拇指指纹都是“Ws”,右手拇指指纹都不是“Ws”的概率是_________.
纹形 拇指
左手 右手 左右手纹形相同
As 20 2 2
Lu,Lr 279 304 250
Wr 3 6 2
Wc 32 27 10
Wt 30 28 9
Ws 59 79 34
Wd 65 37 18
Wp 12 17 8
总人数 500 500 333
28.已知函数的定义域为,若对任意的正实数,函数在上单调递增,则称函数具有性质,给出下列四个结论:
①在上单调递增,则具有性质;
②具有性质不具有性质;
③具有性质不具有性质;
④若函数具有性质,且,则.
其中所有正确结论的序号是_________________.
29.零件分别先在机器上加工,然后在机器上加工,加工所需时间(单位:分钟)如表所示.
①若加工顺序为,则加工完所有零件所需时间最少为分钟;
②改变这5个零件的加工顺序,可以使得加工完所有零件所需时间更少,所需时间最少为_________________分钟,共有_________________种排序方法使得所需时间最少.
机床 零件
1 5
8 3
3 9
4 5
7 6
参考答案
Ⅰ卷
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.【答案】B
【分析】根据补集概念求解出结果.
【详解】因为,
所以,
故选:B.
2.【答案】A
【分析】根据各层的抽样比相同求解出结果.
【详解】因为初中学生1000人抽取了100人,所以抽样比为,
所以高中生抽取人,
故选:A.
3.【答案】C
【分析】根据特称命题的否定是全称命题分析判断.
【详解】由题意可知:命题“”的否定是“”.
故选:C.
4.【答案】C
【分析】先根据的单调性相反排除AD,然后根据幂函数图象判断出的范围,由此可知正确图象.
【详解】因为在同一坐标系中,
所以的单调性一定相反,且图象均不过原点,故排除AD;
在BC选项中,过原点的图象为幂函数的图象,由图象可知,
所以单调递减,单调递增,故排除B,
故选:C.
5.【答案】B
【分析】利用定义判断函数的奇偶性可对A、C判断;利用函数奇偶性的判断并结合函数单调性可对B、D判断.
【详解】对A、C:由,定义域为,所以不是奇函数,故A错误;
定义域为,所以是偶函数,故C错误;
对B、D:,定义域为,所以为奇函数,当时,,且在上单调递减,故B正确;
,定义域为,且,所以为奇函数,且在定义域上为增函数,故D错误;
故选:B.
6.【答案】D
【分析】根据题意结合指、对数函数单调性运算求解.
【详解】因为,
由在上单调递增,可得,即;
由在内单调递增,可得,即;
由在内单调递增,可得,即;
综上所述:.
故选:D.
7.【答案】C
【分析】根据“”与“为奇函数”互相推出的情况判断属于何种条件.
【详解】当时,,定义域为且关于原点对称,
所以,
所以为奇函数;
当为奇函数时,显然定义域为且关于原点对称,所以,
所以,
所以,
由上可知,“”是“为奇函数”的充要条件,
故选:C.
8.【答案】B
第8页/共18页
【分析】先求出的定义域,然后分析的单调性,再根据求解出不等式解集.
【详解】的定义域为,
因为均在上单调递增,
所以在上单调递增,
又因为,所以,
所以不等式解集为,
故选:B.
9.【答案】D
【分析】根据题意得出Koch曲线是由把全体缩小的4个相似图形构成的,再根据题设条件即可得出结果.
【详解】由题意Koch曲线是由把全体缩小的4个相似图形构成的,
因为,即,则,
所以分形维数是.
故选:D.
10.【答案】D
【分析】利用赋值和排除法可得结果
【详解】取,则,
若,则,由,得,
解得,符合条件,排除选项A、C,
取,则,
若时,,由,得,
解得,或,都不符合条件,
若,即,由,
得,即,不符合条件,
若,即,由,
得,解得,或,都不符合条件,
综上,,排除B,选D
故选:D.
二、填空题共5小题,每小题4分,共20分.
11.【答案】
【分析】利用真数大于零列不等式求解即可.
【详解】要使函数有意义,
则,解得,
即函数的定义域是,
故答案为:.
【点睛】本题主要考查对数型复合函数的定义域,属于基础题.
12.【答案】①3 ②>
【分析】空①根据题意分别求出甲乙环境下的15个高度数据,从而求出中位数,即可求解;空②利用标准差公式分别求出,从而求解.
【详解】对空①:由题意得甲环境的幼苗高度为: 31,32,33,33,35,43,44,45,49,55,57,58,59,63,65,其中位数,
乙环境的幼苗高度为: 37,43,44,45,45,47,48,48,49,52,54,54,55,58,60,其中位数,所以;
对空②:甲环境下的幼苗平均高度为:
所以:
甲环境下的幼苗平均高度为:
所以
所以.
故答案为:3;>.
13.【答案】
①0 (即可) ②
【分析】根据题意分析可知函数没有零点,等价于与没有交点,结合对勾函数图象分析求解.
【详解】令,则,
若函数没有零点,等价于与没有交点,
作出的图象,如图所示:
由图象可知:若与没有交点,则,
故答案为:0即可);.
14.【答案】① ②215
【分析】第一个空,作出的图象,由图可知的单调递增区间;第二个空,分和两种情况解不等式.
【详解】作出的图象,由图可知,的单调递增区间为,
当时,,解得,即,
所以,
当时,,解得,
故满足的整数解的个数为215.
故答案为:;215.
15.【答案】①②
【分析】对于①令即可求得定点可判断①的正误;对于②对求导,判断导函数在时的正负即可判断②的正误;对于③由②即可判断正误;对于④以为自变量构造新函数,求导,判断单调性即可判断正误.
【详解】对于①,在中,令,则,过定点,故①正确;
对于②,,当,则为单调递增,故②正确;
对于③,由②知为单调递增,故不存在对称性,故③错误;
对于④,以为自变量,设为,则,
,故的正负取决于,
当,即时,,随着的增大,减小;
当,即时,,随着的增大,增大,故④错误.
故答案为:①②.
三、解答题共4小题,共40分.解答应写出文字说明,演算步骤或证明过程.
16.【答案】(1) (2) (3)
【分析】(1)由题意知总样本数为18,C:古建筑及历史纪念建筑物共有12,利用古典概率从而求解.
(2)由题意可知小王参观A:革命遗址及革命纪念建筑物与小张参观C:古建筑及历史纪念建筑物在同一个区的只有东城区,然后分别求出他们参观东城区的概率,从而求解.
(3)利用分类讨论求出相应的抽到海淀区的概率和抽不到海淀区的概率,从而求解.
【小问1详解】
设选中参观单位恰好为“C:古建筑及历史纪念建筑物”为事件A,
由题意知总共有18,“C:古建筑及历史纪念建筑物”有12,
所以.
【小问2详解】
设两人选择的参观单位恰好在同一个区为事件,由题意可知小王参观:革命遗址及革命纪念建筑物与小张参观:古建筑及历史纪念建筑物在同一个区的只有东城区,
所以小王参观东城区景区的概率为,小张参观东城区景区的概率为,
所以.
【小问3详解】
当抽到的2个都是海淀区的概率为,
当抽到的2个中有1个是海淀区的概率为,
所以,
所以.
17.【答案】(1)
(2)
【分析】(1)先求解出一元二次不等式、绝对值不等式的解集为集合,然后根据并集概念求解出,再根据交集和补集概念求解出;
(2)根据不等式先求解出,然后根据列出关于的不等式组,由此求解出结果.
【小问1详解】
因为,解得,所以,
又因为,解得或,所以,
所以;
又因为,
所以.
【小问2详解】
因为,
所以,
若,则,解得,
所以的取值范围是.
18.【答案】(1)答案见解析
(2)在区间上单调递减,证明见解析
(3)在内有且仅有一个零点,理由见解析
【分析】(1)根据题意结合奇偶性的定义分析求解;
(2)根据单调性的定义分析证明;
(3)根据题意结合单调性以及奇偶性的性质判断在区间上的单调性,再结合零点存在性定理分析判断.
【小问1详解】
令,解得,所以函数的定义域为,
若选①:因为,即为奇函数,
则,
整理得,
注意到对任意上式均成立,可得,解得;
若选②:因为,即为偶函数,
则,
整理得,
注意到对任意上式均成立,可得,解得.
【小问2详解】
若选①:则,可得,
可知函数在区间上单调递减,证明如下:
对任意,且,
则,
因为,则,
可得,即,
所以函数在区间上单调递减;
若选②:则,可得,
可知函数在区间上单调递减,证明如下:
对任意,且,
则,
因为,则,
可得,即,
所以函数在区间上单调递减.
【小问3详解】
若选①:则,则,
由(2)可知在内单调递减,且在定义域内单调递增,
可知在内单调递减,
又因为为奇函数,则在内单调递减,
且在内单调递减,可知在内单调递减,
结合,
可知在内有且仅有一个零点;
若选②:则,则,
由(2)可知在内单调递减,且在定义域内单调递增,
可知在内单调递减,
又因为为偶函数,则在内单调递增,
且在内单调递增,可知在内单调递增,
结合,
可知在内有且仅有一个零点.
19.【答案】(1)唯一交换,理由见解析
(2) (3)
【分析】(1)根据方程解的情况判断即可;
(2)根据“对任意的成立”得到关于的方程,然后设出的解析式,根据方程左右两边对应项相同求解出的值;
(3)根据条件通过分离参数将问题转化为“存在唯一实数,使得”,然后分析的奇偶性,从而确定出,由此可求的值.
【小问1详解】
与关于是唯一交换,理由如下:
因为,
令,所以,解得,
所以有唯一解,
所以与关于是唯一交换.
【小问2详解】
由题意可知,对任意的成立,
即对任意的;
考虑到等式左右两边最高次和最高次项的系数相等,不妨设,
所以,
所以,
所以,所以,即可取,
经检验满足要求,
综上所述,.
【小问3详解】
当时,,
因为与关于唯一交换,
所以存在唯一实数,使得,
即存在唯一实数,使得,
即存在唯一实数,使得;
令,且定义域均为,
又
,
所以都是偶函数,所以为偶函数,
因此,若存在唯一实数使得,只能是,
所以,
综上所述,的取值为.
【点睛】关键点点睛:本题考查函数的新定义,涉及方程解以及函数奇偶性等相关问题,对学生的理解与计算能力要求较高,难度较大.“新定义”题型的关键是根据新定义的概念、新公式、新定理、新法则、新运算去解决问题,本题第二问可以从方程左右两边对应相等入手,第三问则可以从函数的奇偶性入手进行分析.
Ⅱ卷
一、选择题(共5小题,每小题5分,共25分)
20.B 21.B 22.C 23.D 24.D
二、填空题(共5小题,每小题5分,共25分)
25.2; 26.;
27.; 28.②④
29.32;29;7
同课章节目录
