5.3 图形变换的简单应用 课件(共21张PPT)
文档属性
| 名称 | 5.3 图形变换的简单应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-08 17:55:14 | ||
图片预览








文档简介
(共21张PPT)
5.3 图形变换的简单应用
1.会识别图案中的基础图形,通过对图形的识别与欣赏,进一步加深图形的平移、旋转和轴反射概念与性质的理解.
2.能将一些基础图形经过平移、旋转和轴反射等变换设计一些美丽的图案.
3.通过图形的三种变换提高学生的应用意识.
4.欣赏轴对称、平移、旋转等变换在现实生活中的应用.
【教学重点】运用图形变换设计图案.
【教学难点】运用图形变换设计图案.
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动
称为平移。
平移的概念:
平移的性质:
1、平移不改变图形的大小和形状。
2、对应点所连的线平行且相等。
3、对应线段平行且相等。
4、对应角相等。
旋转
定义
三要素:
旋转中心,旋转方向和旋转角度.
性质
旋转前后的图形形状和大小不变;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角都等于旋转角.
欣赏下列图案,说出它们分别是由哪个基础图形经过怎样的
变换得到的,在图中把基础图形标出来.
(1)
观察
(2)
(3)
(1)
(2)
(3)
图(1)是由正方形图案 作平移得到的.
图(2)是由 图作轴对称变换得到的.
图(3)是中华人民共和国香港特别行政区区徽,可由一个紫荆花瓣 绕中心点O按顺时针方向依次旋转72°,144°, 216°,288°而得到.
【例】以图的右边缘所在的直线为轴,将该图形向右作
轴对称变换,再绕中心O按顺时针方向旋转180°,所得到的
图形是( )
【分析】将图以右边缘所在的直线为轴作轴对称变换,得到图 ,
A
再绕中心O按顺时针方向旋转180°,得到图 .
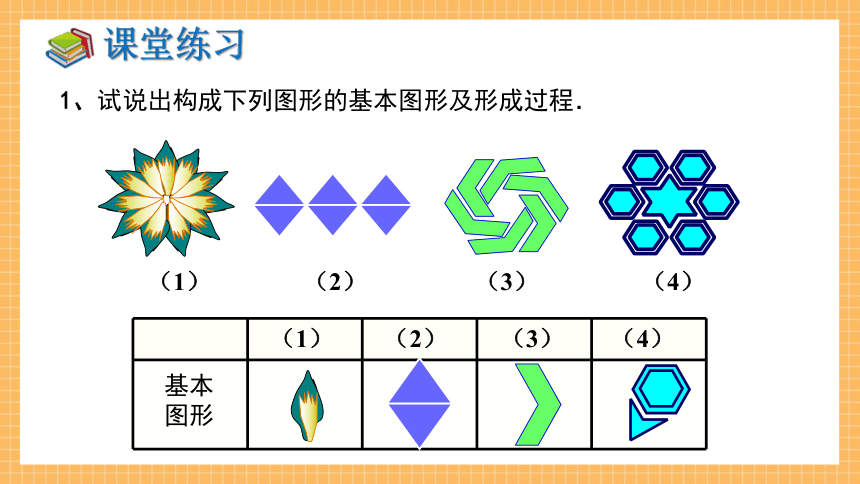
1、试说出构成下列图形的基本图形及形成过程.
(1)
(2)
(3)
(4)
基本图形
(1)
(2)
(3)
(4)
基本图案
图案的形成过程
分析图案的形成过程
对于这三种图形变换一般从定义区分即可.分清图形变换的几个最基本概念是解题的关键.
图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案,希望同学们认真分析,精心设计出漂亮的图案来.
2、如图是一种正方形的瓷砖.
(1)请用 4 块所给瓷砖拼一个正方形图案(至少设计 3 种不同的图案);
(2)如果给你 16 块这样的正方形瓷砖,要求设计的图案为轴对称图形,你可以设计出来吗?
(1)请用 4 块所给瓷砖拼一个正方形图案(至少设计 3 种不同的图案);
圆弧与扇形的对称轴是过弧中点和圆心的直线.角的对称轴是角平分线所在的直线.菱形和等腰梯形是轴对称图形.
解
3、如图,下列几何图形中,一定是轴对称图形的有( ).
A.2个 B.3个 C.4个 D.5个
D
1.下图中只能用其中一部分平移可以得到的是( ).
B
D
A
B
C
2、当一个字母F旋转90度或180度时,其中旋转后位置正确的是( )
A
B
C
D
C
3.下图右边的 3 个三角形是由图 a 的三角形经过平移、旋转和轴对称变换而得到,分别指出这些图形变换的名称, 并指出其对应的边.
平移变换
旋转变换
轴对称变换
4.起重机将重物垂直提起,这可以看作是数学上的( )
A.轴对称 B.平移
C.旋转 D.变形
B
5、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,以三个正三角形的公
共顶点为旋转中心,分别按顺时针、逆时针方向旋转600,即可
得到该图案。
6. 如图,在四边形 ABCD 中,
AC ⊥ BD于点 E,BE = DE.
已知 AC = 10 cm,BD = 8 cm,
求阴影部分的面积.
解:阴影部分的面积是 20 cm2.
图形间的变换关系
1 旋转——旋转中心、方向、角度和次数
2 平移——平移的方向、距离和次数
3 轴对称——对称轴
4 旋转与平移的组合
5 旋转与轴对称的组合
6 轴对称与平移的组合
找准基本图形
1. 习题5.3中第1、4、5题.
2.完成同步练习册中本课时的练习.
5.3 图形变换的简单应用
1.会识别图案中的基础图形,通过对图形的识别与欣赏,进一步加深图形的平移、旋转和轴反射概念与性质的理解.
2.能将一些基础图形经过平移、旋转和轴反射等变换设计一些美丽的图案.
3.通过图形的三种变换提高学生的应用意识.
4.欣赏轴对称、平移、旋转等变换在现实生活中的应用.
【教学重点】运用图形变换设计图案.
【教学难点】运用图形变换设计图案.
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动
称为平移。
平移的概念:
平移的性质:
1、平移不改变图形的大小和形状。
2、对应点所连的线平行且相等。
3、对应线段平行且相等。
4、对应角相等。
旋转
定义
三要素:
旋转中心,旋转方向和旋转角度.
性质
旋转前后的图形形状和大小不变;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角都等于旋转角.
欣赏下列图案,说出它们分别是由哪个基础图形经过怎样的
变换得到的,在图中把基础图形标出来.
(1)
观察
(2)
(3)
(1)
(2)
(3)
图(1)是由正方形图案 作平移得到的.
图(2)是由 图作轴对称变换得到的.
图(3)是中华人民共和国香港特别行政区区徽,可由一个紫荆花瓣 绕中心点O按顺时针方向依次旋转72°,144°, 216°,288°而得到.
【例】以图的右边缘所在的直线为轴,将该图形向右作
轴对称变换,再绕中心O按顺时针方向旋转180°,所得到的
图形是( )
【分析】将图以右边缘所在的直线为轴作轴对称变换,得到图 ,
A
再绕中心O按顺时针方向旋转180°,得到图 .
1、试说出构成下列图形的基本图形及形成过程.
(1)
(2)
(3)
(4)
基本图形
(1)
(2)
(3)
(4)
基本图案
图案的形成过程
分析图案的形成过程
对于这三种图形变换一般从定义区分即可.分清图形变换的几个最基本概念是解题的关键.
图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案,希望同学们认真分析,精心设计出漂亮的图案来.
2、如图是一种正方形的瓷砖.
(1)请用 4 块所给瓷砖拼一个正方形图案(至少设计 3 种不同的图案);
(2)如果给你 16 块这样的正方形瓷砖,要求设计的图案为轴对称图形,你可以设计出来吗?
(1)请用 4 块所给瓷砖拼一个正方形图案(至少设计 3 种不同的图案);
圆弧与扇形的对称轴是过弧中点和圆心的直线.角的对称轴是角平分线所在的直线.菱形和等腰梯形是轴对称图形.
解
3、如图,下列几何图形中,一定是轴对称图形的有( ).
A.2个 B.3个 C.4个 D.5个
D
1.下图中只能用其中一部分平移可以得到的是( ).
B
D
A
B
C
2、当一个字母F旋转90度或180度时,其中旋转后位置正确的是( )
A
B
C
D
C
3.下图右边的 3 个三角形是由图 a 的三角形经过平移、旋转和轴对称变换而得到,分别指出这些图形变换的名称, 并指出其对应的边.
平移变换
旋转变换
轴对称变换
4.起重机将重物垂直提起,这可以看作是数学上的( )
A.轴对称 B.平移
C.旋转 D.变形
B
5、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,以三个正三角形的公
共顶点为旋转中心,分别按顺时针、逆时针方向旋转600,即可
得到该图案。
6. 如图,在四边形 ABCD 中,
AC ⊥ BD于点 E,BE = DE.
已知 AC = 10 cm,BD = 8 cm,
求阴影部分的面积.
解:阴影部分的面积是 20 cm2.
图形间的变换关系
1 旋转——旋转中心、方向、角度和次数
2 平移——平移的方向、距离和次数
3 轴对称——对称轴
4 旋转与平移的组合
5 旋转与轴对称的组合
6 轴对称与平移的组合
找准基本图形
1. 习题5.3中第1、4、5题.
2.完成同步练习册中本课时的练习.
