四年级下册数学北师大版6.4 平均数课件(共27张PPT)
文档属性
| 名称 | 四年级下册数学北师大版6.4 平均数课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-06 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
北师版四年级数学下册
数据的表示和分析
第4节 平均数(1)
汇报人:XXX 时间:XXXXX
1.结合解决问题的过程,了解平均数的意义。
2.能结合简单的统计图表,解决一些简单的与平均数有关的实际问题。
3.进一步积累数据分析的活动经验
4.会计算简单数据的平均数,解决与平均数有关的实际问题。
5.理解平均数的意义。
同学们,你们听说过平均数吗?你知道它有什么作用吗?你再日常生活中使用过吗?其实它里面有很多有趣的故事,今天我们就一起来探究。
课堂导入
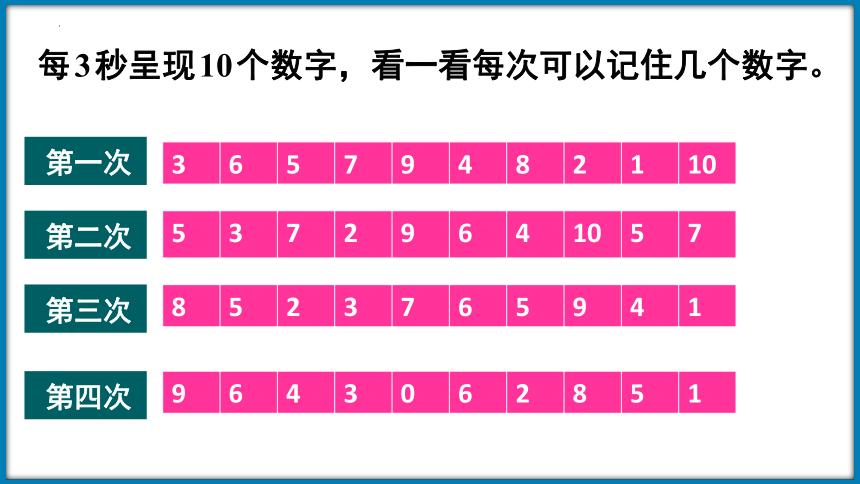
每3秒呈现10个数字,看一看每次可以记住几个数字。
第一次
3 6 5 7 9 4 8 2 1 10
第二次
5 3 7 2 9 6 4 10 5 7
第三次
8 5 2 3 7 6 5 9 4 1
第四次
9 6 4 3 0 6 2 8 5 1
每3秒呈现10个数字,看一看每次可以记住几个数字。
每3秒呈现10个数字,看一看每次可以记住几个数字。
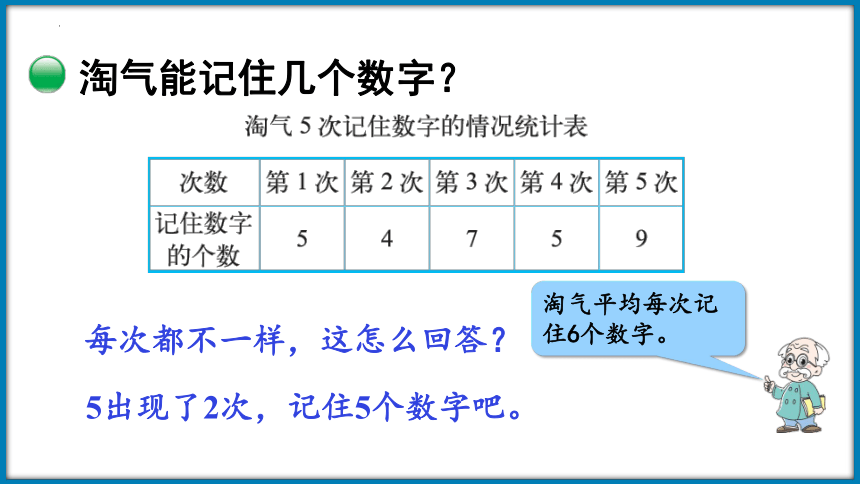
淘气能记住几个数字?
每次都不一样,这怎么回答?
5出现了2次,记住5个数字吧。
淘气平均每次记住6个数字。
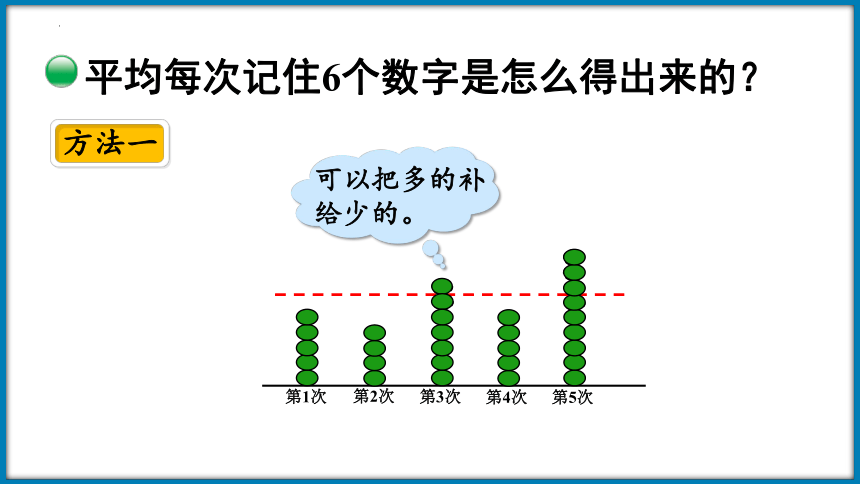
平均每次记住6个数字是怎么得出来的?
第1次
第2次
第3次
第4次
第5次
方法一
可以把多的补给少的。
平均每次记住6个数字是怎么得出来的?
方法二
列式计算
“平均数=总个数÷总次数”
(5+4+7+5+9)÷5
=30÷5
=6(个)
可是淘气哪一次也没有记住6个数字啊!这是怎么回事呢?
你能帮忙解决机灵狗的问题吗?
“6个”是几次“匀”出来的。
这就是平均数,它是一组数据平均水平的代表。
哦,我明白了。
平均数不是一个实际的数,而是借助平均分的意义通过计算得到反应一组数据整体情况的一个“虚拟”的数。
一般情况下,平均数介于一组数据的最大值和最小值之间。
一组数据的和除以这组数据的个数所得的商就是平均数。
什么是平均数呢?平均数有什么特征?
区分“平均分”和“平均数”
(1)把15支铅笔平均分给3个小朋友,每个小朋友 分得5支铅笔。
这里的5支表示平均分的结果,是每个小朋友实际分得的支数。
(2)3个小朋友一共有15支铅笔,平均每个孩子有5支铅笔。
这里的5支是平均数,它并不代表每人一定有5支铅笔。
说一说生活中你在哪里见到过平均数。
1.下面四幅图,都是梦梦星期一至星期五获得奖励的笑脸
个数情况统计图。虚线所指的位置能够表示梦梦本周平
均每天得到笑脸个数的是( D )。
D
A. B. C. D.
课堂练习
解析:根据统计图可知,星期一得到4个,星期二得到7个,星期三
得到5个,星期四得到6个,星期五得到8个,根据移多补少的方
法,把星期二得到的笑脸给星期三1个,把星期五得到的笑脸给星
期一2个,这样每天都是6个,从而得到,D选项中虚线所指的位置
能够表示梦梦本周平均每天得到笑脸的个数。
A. B. C. D.
2.如图是四(1)班上课积极动脑的几位同学获得点赞卡的情
况,平均每人获得了多少张点赞卡?
(1)通过( 移多补少 )的方法可以看出平均每人获得了
( 6 )张点赞卡。
解析:求平均数的方法:移多补少法;
(2)列式解答:(7+4+5+8)÷4=6(张)
答:平均每人获得了6张点赞卡。
解析:求平均数的方法:公式法:总数÷份数=平均数。
移多补少
6
(7+4+5+8)÷4=6(张)
(1)一条小河平均水深1米,小强身高1.2米,他不会游泳,但他下河玩耍肯定安全。( )
(2)城南小学全体同学向希望工程捐款,平均每人捐款3元。那么,全校每个同学一定都捐了3元。( )
×
×
3.火眼金睛辨对错。
平均数代表的是一组数据的整体水平,不能说这组数据里的每个数都与平均数相等。
我们组同学的平均体重是35千克。
小明
4.小明的体重一定比小强轻吗?
我们组同学的平均体重是37千克。
小强
所以小明的体重不一定比小强轻。
平均体重的是一组同学体重的整体水平,并不能说明小强和小明的体重水平。
5.刘叔叔第一次直播卖水果卖了1088千克,第二次和第三
次直播平均每次卖956千克,这三次直播平均每次卖出水果
多少吨?
(956×2+1088)÷3=1000(千克)
1000千克=1吨
答:这三次直播平均每次卖出水果1吨。
6.下表是典典期末考试部分学科的成绩(单位:分),典典数
学期末成绩是多少分?
语文 数学 英语 平均分
91 97 94
94×3-91-97=94(分)
答:典典数学期末成绩是94分。
解析:已知平均分为94分,用平均分乘3即可求出3科的总分,然后用总分减去语文、英语期末成绩,即可求出数学期末成绩。
7.高考数学全国卷满分150分,现有5名学生的高考数学成绩的
平均分是118,把成绩按分值从高到低的顺序排列,前两名学
生的平均分是128,最后两名学生的平均分是107,成绩排在中
间的那名学生考了多少分?
118×5=590(分)
128×2=256(分)
107×2=214(分)
590-256-214=120(分)
1.同同以每分60 m的速度从新城东路走到新城西路,用了12分,然后以每分90 m的速度沿原路返回。这次往返中,同同平均每分走多少米?
60×12=720(m)
720÷90=8(分)
720×2÷(12+8)=72(m)
答:同同平均每分走72 m。
解析:因为往返的路程相等,首先根据“路程=时间×速度”,用去时的时间乘去时的速度求出新城东路到新城西路的路程,再根据“路程÷速度=时间”,求出原路返回时用的时间,用路程乘2就是往返的总路程,再用往返的总路程除以往返的总时间就是平均每分走的路程。
思维拓展
2.在科技节中学校开展科学知识竞赛,四(1)班派出数名学生组成科技小队,参加比赛。蓝蓝也是其中的一员,小队的最终平均分是86分,蓝蓝得了96分,该小队不算蓝蓝平均分是84分,这个小队一共有多少人?
(96-84)÷(86-84)=6(人)
答:这个小队一共有6人。
解析:蓝蓝得了96分,不算蓝蓝的平均分是84分,说明把96-84=12(分)平均分给了这个小队的每一个队员,所以平均分从84分变成了86分,说明每个队员得到了86-84=2(分),因此这个小队一共有12÷2=6(人)。
同学们,这节课你们学会了哪些知识?
平均数的意义
一组数据的和除以这组数据的总个数,所得的商就是这组数据的平均数,平均数是一组数据平均水平的代表。
求平均数的方法
移多补少法:把多的拿出一部分给少的,直到每个数据都相等,即可求出平均数。
计算法:先求出一组数据的和,再除以这组数据的总个数。
同学们,这节课你们学会了哪些知识?
课堂小结
北师版四年级数学下册
数据的表示和分析
第4节 平均数(1)
汇报人:XXX 时间:XXXXX
1.结合解决问题的过程,了解平均数的意义。
2.能结合简单的统计图表,解决一些简单的与平均数有关的实际问题。
3.进一步积累数据分析的活动经验
4.会计算简单数据的平均数,解决与平均数有关的实际问题。
5.理解平均数的意义。
同学们,你们听说过平均数吗?你知道它有什么作用吗?你再日常生活中使用过吗?其实它里面有很多有趣的故事,今天我们就一起来探究。
课堂导入
每3秒呈现10个数字,看一看每次可以记住几个数字。
第一次
3 6 5 7 9 4 8 2 1 10
第二次
5 3 7 2 9 6 4 10 5 7
第三次
8 5 2 3 7 6 5 9 4 1
第四次
9 6 4 3 0 6 2 8 5 1
每3秒呈现10个数字,看一看每次可以记住几个数字。
每3秒呈现10个数字,看一看每次可以记住几个数字。
淘气能记住几个数字?
每次都不一样,这怎么回答?
5出现了2次,记住5个数字吧。
淘气平均每次记住6个数字。
平均每次记住6个数字是怎么得出来的?
第1次
第2次
第3次
第4次
第5次
方法一
可以把多的补给少的。
平均每次记住6个数字是怎么得出来的?
方法二
列式计算
“平均数=总个数÷总次数”
(5+4+7+5+9)÷5
=30÷5
=6(个)
可是淘气哪一次也没有记住6个数字啊!这是怎么回事呢?
你能帮忙解决机灵狗的问题吗?
“6个”是几次“匀”出来的。
这就是平均数,它是一组数据平均水平的代表。
哦,我明白了。
平均数不是一个实际的数,而是借助平均分的意义通过计算得到反应一组数据整体情况的一个“虚拟”的数。
一般情况下,平均数介于一组数据的最大值和最小值之间。
一组数据的和除以这组数据的个数所得的商就是平均数。
什么是平均数呢?平均数有什么特征?
区分“平均分”和“平均数”
(1)把15支铅笔平均分给3个小朋友,每个小朋友 分得5支铅笔。
这里的5支表示平均分的结果,是每个小朋友实际分得的支数。
(2)3个小朋友一共有15支铅笔,平均每个孩子有5支铅笔。
这里的5支是平均数,它并不代表每人一定有5支铅笔。
说一说生活中你在哪里见到过平均数。
1.下面四幅图,都是梦梦星期一至星期五获得奖励的笑脸
个数情况统计图。虚线所指的位置能够表示梦梦本周平
均每天得到笑脸个数的是( D )。
D
A. B. C. D.
课堂练习
解析:根据统计图可知,星期一得到4个,星期二得到7个,星期三
得到5个,星期四得到6个,星期五得到8个,根据移多补少的方
法,把星期二得到的笑脸给星期三1个,把星期五得到的笑脸给星
期一2个,这样每天都是6个,从而得到,D选项中虚线所指的位置
能够表示梦梦本周平均每天得到笑脸的个数。
A. B. C. D.
2.如图是四(1)班上课积极动脑的几位同学获得点赞卡的情
况,平均每人获得了多少张点赞卡?
(1)通过( 移多补少 )的方法可以看出平均每人获得了
( 6 )张点赞卡。
解析:求平均数的方法:移多补少法;
(2)列式解答:(7+4+5+8)÷4=6(张)
答:平均每人获得了6张点赞卡。
解析:求平均数的方法:公式法:总数÷份数=平均数。
移多补少
6
(7+4+5+8)÷4=6(张)
(1)一条小河平均水深1米,小强身高1.2米,他不会游泳,但他下河玩耍肯定安全。( )
(2)城南小学全体同学向希望工程捐款,平均每人捐款3元。那么,全校每个同学一定都捐了3元。( )
×
×
3.火眼金睛辨对错。
平均数代表的是一组数据的整体水平,不能说这组数据里的每个数都与平均数相等。
我们组同学的平均体重是35千克。
小明
4.小明的体重一定比小强轻吗?
我们组同学的平均体重是37千克。
小强
所以小明的体重不一定比小强轻。
平均体重的是一组同学体重的整体水平,并不能说明小强和小明的体重水平。
5.刘叔叔第一次直播卖水果卖了1088千克,第二次和第三
次直播平均每次卖956千克,这三次直播平均每次卖出水果
多少吨?
(956×2+1088)÷3=1000(千克)
1000千克=1吨
答:这三次直播平均每次卖出水果1吨。
6.下表是典典期末考试部分学科的成绩(单位:分),典典数
学期末成绩是多少分?
语文 数学 英语 平均分
91 97 94
94×3-91-97=94(分)
答:典典数学期末成绩是94分。
解析:已知平均分为94分,用平均分乘3即可求出3科的总分,然后用总分减去语文、英语期末成绩,即可求出数学期末成绩。
7.高考数学全国卷满分150分,现有5名学生的高考数学成绩的
平均分是118,把成绩按分值从高到低的顺序排列,前两名学
生的平均分是128,最后两名学生的平均分是107,成绩排在中
间的那名学生考了多少分?
118×5=590(分)
128×2=256(分)
107×2=214(分)
590-256-214=120(分)
1.同同以每分60 m的速度从新城东路走到新城西路,用了12分,然后以每分90 m的速度沿原路返回。这次往返中,同同平均每分走多少米?
60×12=720(m)
720÷90=8(分)
720×2÷(12+8)=72(m)
答:同同平均每分走72 m。
解析:因为往返的路程相等,首先根据“路程=时间×速度”,用去时的时间乘去时的速度求出新城东路到新城西路的路程,再根据“路程÷速度=时间”,求出原路返回时用的时间,用路程乘2就是往返的总路程,再用往返的总路程除以往返的总时间就是平均每分走的路程。
思维拓展
2.在科技节中学校开展科学知识竞赛,四(1)班派出数名学生组成科技小队,参加比赛。蓝蓝也是其中的一员,小队的最终平均分是86分,蓝蓝得了96分,该小队不算蓝蓝平均分是84分,这个小队一共有多少人?
(96-84)÷(86-84)=6(人)
答:这个小队一共有6人。
解析:蓝蓝得了96分,不算蓝蓝的平均分是84分,说明把96-84=12(分)平均分给了这个小队的每一个队员,所以平均分从84分变成了86分,说明每个队员得到了86-84=2(分),因此这个小队一共有12÷2=6(人)。
同学们,这节课你们学会了哪些知识?
平均数的意义
一组数据的和除以这组数据的总个数,所得的商就是这组数据的平均数,平均数是一组数据平均水平的代表。
求平均数的方法
移多补少法:把多的拿出一部分给少的,直到每个数据都相等,即可求出平均数。
计算法:先求出一组数据的和,再除以这组数据的总个数。
同学们,这节课你们学会了哪些知识?
课堂小结
