6.1.1 平均数(第2课时) 课件(共25张PPT)
文档属性
| 名称 | 6.1.1 平均数(第2课时) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-06 16:14:32 | ||
图片预览







文档简介
(共25张PPT)
6.1.1 平均数
第2课时 加权平均数
1.体会“权”的差异对平均数的影响,算术平均数和加权平均数的联系与区别,能应用加权平均数解释现实生活中的一些简单现象,并能用它解决一些实际问题.
2.通过独立思考和小组讨论获得基本数学活动经验和交流合作的能力.
3.进一步增强统计意识和数学应用能力,体会数学与自然及人类社会的密切联系,了解数学的价值,加深对数学的理解和学好数学的信心.
【教学重点】“权”的意义和加权平均数的计算.
【教学难点】“权”的意义和加权平均数的计算.
1. 算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2. 计算公式:
x =
x1+x2+ x3+ ··· + xn
n
3. 计算器操作:
开机、
清除、
输数据、
读信息.
选择功能、
课本P139“动脑筋”:
学校举行运动会,入场式中有七年级的一个队列.已知这个队列共100人,排成10行,每行10人.其中前两行同学的身高都是160cm,接着3行同学的身高都是155cm,最后5行同学的身高都是150cm.怎样求这个队列的平均身高?
用 表示平均身高,则
在上面的算式中,0.2,0.3,0.5分别表示160,155,150这三个数在数据组中所占的比例,分别称它们为这三个数的权数:
160的权数是0.2
155的权数是0.3
150的权数是0.5
三个权数之和为0.2+0.3+0.5=1.
153.5是160,155,150分别以0.2,0.3,0.5为权的加权平均数.
权数的基本性质:
1、非负性:0
2、归一性:各权数之和为1;
3、“权”越大,对平均数的影响就越大。
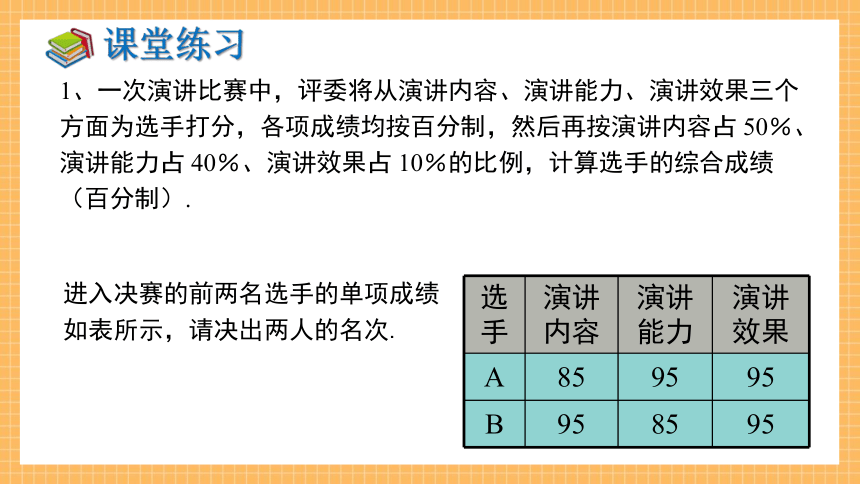
1、一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占 50%、演讲能力占 40%、演讲效果占 10%的比例,计算选手的综合成绩(百分制).
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
进入决赛的前两名选手的单项成绩如表所示,请决出两人的名次.
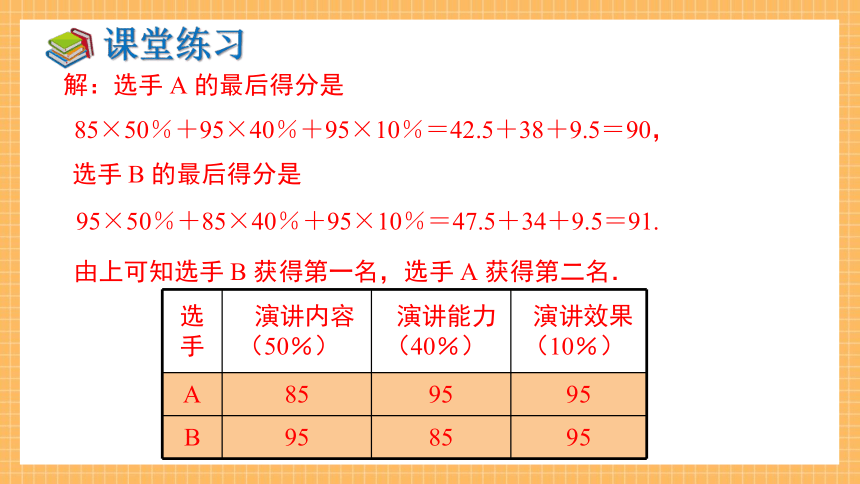
解:选手 A 的最后得分是
85×50%+95×40%+95×10%=42.5+38+9.5=90,
选手 B 的最后得分是
95×50%+85×40%+95×10%=47.5+34+9.5=91.
由上可知选手 B 获得第一名,选手 A 获得第二名.
选手 演讲内容 (50%) 演讲能力 (40%) 演讲效果
(10%)
A 85 95 95
B 95 85 95
有一组数据如下:
1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.
(1)计算这组数据的平均数.
(2)这组数据中1.60,1.64,1.68的权数分别是多少 求出这组数据的加权平均数.
(3)这组数据的平均数和加权平均数有什么关系?
(1)这组数据的平均数为
有一组数据如下:
1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.
(2)这组数据中1.60,1.64,1.68的权数分别是多少?求出这组数据的加权平均数.
这组数据的加权平均数为
有一组数据如下:
1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.
(3)这组数据的平均数和加权平均数有什么关系?
这组数据的平均数为
这组数据的加权平均数为
(3)这组数据的平均数和加权平均数相等,都等于1.64,意义也恰好完全相同.但我们不能把求加权平均数看成是求平均数的简便方法,在许多实际问题中,权数及相应的加权平均数都有特殊的含义.平均数可看做是权数相同的加权平均数.
你能说说平均数与加权平均数的区别和联系吗?
2. 在实际问题中,各项的权数不相等时,计算平均数时就要采用加权平均数;当各项权数相等时,直接计算算术平均数就可以了.
1. 平均数可以看做是加权平均数的一种特殊情况(它特殊在各项的权数相等);
议一议
课本P141
例2:某纺织厂订购一批棉花,棉花纤维长短不一,主要有3cm,5cm,6cm三种长度.随意地取出10g棉花并测出三种长度的棉花纤维的含量,得到下面的结果:
纤维长度(cm) 3 5 6
含量(g) 2.5 4 3.5
问:这批棉花纤维的平均长度是多少?
解:这批棉花纤维的平均长度是
答:这批棉花纤维的平均长度是4.85cm.
1、一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72
2、甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A、3.88元 B、4.3元 C、8.7元 D、8.8元
C
A
3. 一组数据为 10,8,9,12,13,10,8,则这组数据的平均数是_____.
解析:
解析:
10
17
4. 已知一组数据 4,13,24 的权数分别是
则这组数据的加权平均数是_____.
5、某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定
C
6. 某公司有 15 名员工,他们所在的部门及相应每人所创的年利润(万元)如下表:
部门 A B C D E F G
人数 1 1 2 2 2 2 5
年利润/人 200 40 25 20 15 15 12
该公司每人所创年利润的平均数是_____万元.
30
7、某校规定学生的数学期末总评成绩由三部分组成。平时参与数学活动情况占2 5 %,作业完成情况占35%,期末考试成绩占40%。小明平时参与数学活动、作业完成情况、期末考试成绩得分依次为84分、92分、88分。则小明数学期末总评成绩是多少分?
解:X= 2 5 % ×84 + 35% ×92 + 40% ×88
=21+32.2+35.2
=88.4(分)
答小明数学期末总评成绩是88.4分。
8. 某次歌唱比赛,两名选手的成绩如下:
(1)若按三项平均数取第一名,则_______是第一名.
测试选手 测试成绩 创新 唱功 综合知识
A 72 85 67
B 85 74 70
选手 B
解:
所以,此时第一名是选手 A.
(2)若三项测试得分按 3 : 6 : 1 的比例确定个人的测试成绩,此时第一名是谁?
9.某出版社给一本书的作者发稿费,全书20万字,其中正文占总字数的 ,每千字50元;答案部分占总字数的 ,每千字30元.问全书平均每千字多少元?
答:全书平均每千字46元.
解:因为20万=200千
1. 习题6.1中第1、3题.
2.完成同步练习册中本课时的练习.
6.1.1 平均数
第2课时 加权平均数
1.体会“权”的差异对平均数的影响,算术平均数和加权平均数的联系与区别,能应用加权平均数解释现实生活中的一些简单现象,并能用它解决一些实际问题.
2.通过独立思考和小组讨论获得基本数学活动经验和交流合作的能力.
3.进一步增强统计意识和数学应用能力,体会数学与自然及人类社会的密切联系,了解数学的价值,加深对数学的理解和学好数学的信心.
【教学重点】“权”的意义和加权平均数的计算.
【教学难点】“权”的意义和加权平均数的计算.
1. 算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2. 计算公式:
x =
x1+x2+ x3+ ··· + xn
n
3. 计算器操作:
开机、
清除、
输数据、
读信息.
选择功能、
课本P139“动脑筋”:
学校举行运动会,入场式中有七年级的一个队列.已知这个队列共100人,排成10行,每行10人.其中前两行同学的身高都是160cm,接着3行同学的身高都是155cm,最后5行同学的身高都是150cm.怎样求这个队列的平均身高?
用 表示平均身高,则
在上面的算式中,0.2,0.3,0.5分别表示160,155,150这三个数在数据组中所占的比例,分别称它们为这三个数的权数:
160的权数是0.2
155的权数是0.3
150的权数是0.5
三个权数之和为0.2+0.3+0.5=1.
153.5是160,155,150分别以0.2,0.3,0.5为权的加权平均数.
权数的基本性质:
1、非负性:0
2、归一性:各权数之和为1;
3、“权”越大,对平均数的影响就越大。
1、一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占 50%、演讲能力占 40%、演讲效果占 10%的比例,计算选手的综合成绩(百分制).
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
进入决赛的前两名选手的单项成绩如表所示,请决出两人的名次.
解:选手 A 的最后得分是
85×50%+95×40%+95×10%=42.5+38+9.5=90,
选手 B 的最后得分是
95×50%+85×40%+95×10%=47.5+34+9.5=91.
由上可知选手 B 获得第一名,选手 A 获得第二名.
选手 演讲内容 (50%) 演讲能力 (40%) 演讲效果
(10%)
A 85 95 95
B 95 85 95
有一组数据如下:
1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.
(1)计算这组数据的平均数.
(2)这组数据中1.60,1.64,1.68的权数分别是多少 求出这组数据的加权平均数.
(3)这组数据的平均数和加权平均数有什么关系?
(1)这组数据的平均数为
有一组数据如下:
1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.
(2)这组数据中1.60,1.64,1.68的权数分别是多少?求出这组数据的加权平均数.
这组数据的加权平均数为
有一组数据如下:
1.60,1.60,1.60,1.64,1.64,1.68,1.68,1.68.
(3)这组数据的平均数和加权平均数有什么关系?
这组数据的平均数为
这组数据的加权平均数为
(3)这组数据的平均数和加权平均数相等,都等于1.64,意义也恰好完全相同.但我们不能把求加权平均数看成是求平均数的简便方法,在许多实际问题中,权数及相应的加权平均数都有特殊的含义.平均数可看做是权数相同的加权平均数.
你能说说平均数与加权平均数的区别和联系吗?
2. 在实际问题中,各项的权数不相等时,计算平均数时就要采用加权平均数;当各项权数相等时,直接计算算术平均数就可以了.
1. 平均数可以看做是加权平均数的一种特殊情况(它特殊在各项的权数相等);
议一议
课本P141
例2:某纺织厂订购一批棉花,棉花纤维长短不一,主要有3cm,5cm,6cm三种长度.随意地取出10g棉花并测出三种长度的棉花纤维的含量,得到下面的结果:
纤维长度(cm) 3 5 6
含量(g) 2.5 4 3.5
问:这批棉花纤维的平均长度是多少?
解:这批棉花纤维的平均长度是
答:这批棉花纤维的平均长度是4.85cm.
1、一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72
2、甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A、3.88元 B、4.3元 C、8.7元 D、8.8元
C
A
3. 一组数据为 10,8,9,12,13,10,8,则这组数据的平均数是_____.
解析:
解析:
10
17
4. 已知一组数据 4,13,24 的权数分别是
则这组数据的加权平均数是_____.
5、某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、70 D、无法确定
C
6. 某公司有 15 名员工,他们所在的部门及相应每人所创的年利润(万元)如下表:
部门 A B C D E F G
人数 1 1 2 2 2 2 5
年利润/人 200 40 25 20 15 15 12
该公司每人所创年利润的平均数是_____万元.
30
7、某校规定学生的数学期末总评成绩由三部分组成。平时参与数学活动情况占2 5 %,作业完成情况占35%,期末考试成绩占40%。小明平时参与数学活动、作业完成情况、期末考试成绩得分依次为84分、92分、88分。则小明数学期末总评成绩是多少分?
解:X= 2 5 % ×84 + 35% ×92 + 40% ×88
=21+32.2+35.2
=88.4(分)
答小明数学期末总评成绩是88.4分。
8. 某次歌唱比赛,两名选手的成绩如下:
(1)若按三项平均数取第一名,则_______是第一名.
测试选手 测试成绩 创新 唱功 综合知识
A 72 85 67
B 85 74 70
选手 B
解:
所以,此时第一名是选手 A.
(2)若三项测试得分按 3 : 6 : 1 的比例确定个人的测试成绩,此时第一名是谁?
9.某出版社给一本书的作者发稿费,全书20万字,其中正文占总字数的 ,每千字50元;答案部分占总字数的 ,每千字30元.问全书平均每千字多少元?
答:全书平均每千字46元.
解:因为20万=200千
1. 习题6.1中第1、3题.
2.完成同步练习册中本课时的练习.
