2024年云南省初中学业水平考试数学试题仿真练习卷(含解析)
文档属性
| 名称 | 2024年云南省初中学业水平考试数学试题仿真练习卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-06 22:12:56 | ||
图片预览



文档简介
2024年云南省初中学业水平考试数学试题仿真练习卷
(全卷三个大题,共24个小题,共8页;满分100分,考试用时120分钟)
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,
则分别叫做正数与负数.如果收入100元记作元,那么元表示( )
A.支出80元 B.收入80元 C.支出100元 D.收入100元
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,
若∠1=60°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
3 . 第届亚运会将于年月日至月日在中国浙江省杭州市举行,
杭州奥体博览城游泳馆区建筑总面积平方米,将数用科学记数法表示为( )
A. B. C. D.
4 .如图所示的物体,其主视图是( )
A.B. C. D.
5. 下列计算正确的是( )
A. B. C. D.
6. 某次数学测试共有5道题目,下面是901班30名同学的答对题数情况统计:
答对题数(道) 0 1 2 3 4 5
人数(人) 1 2 4 9 11 3
同学答对题数的众数和中位数分别是( )
A.4道,4道 B.11道,3道 C.4道,3道 D.11道,11道
7. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B.且 C.且 D.
8. 已知、两点均在反比例函数的图象上,则的值为( )
A. B. C. D.
如图,两点被池塘隔开,三点不共线.设的中点分别为.
若米,则( )
A. 4米 B. 6米 C. 8米 D. 10米
《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:
把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天:
如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.
设规定时间为天,则可列方程为( )
A. B. C. D.
11. 如图,等边的三个顶点都在上,是的直径.若,则劣弧的长是( )
A. B. C. D.
12 . 观察下列算式:,,,,,,,,…,
根据上述算式中的规律,你认为的末位数字是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题2分,共8分)
13. 在函数中,自变量x的取值范围是 .
14. 在直角中,,,,求为_______
15. 分解因式: .
16. 如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
三、解答题(本大题共8小题,共56分)
17. 计算:.
18. 如图,点在一条直线上,,求证:.
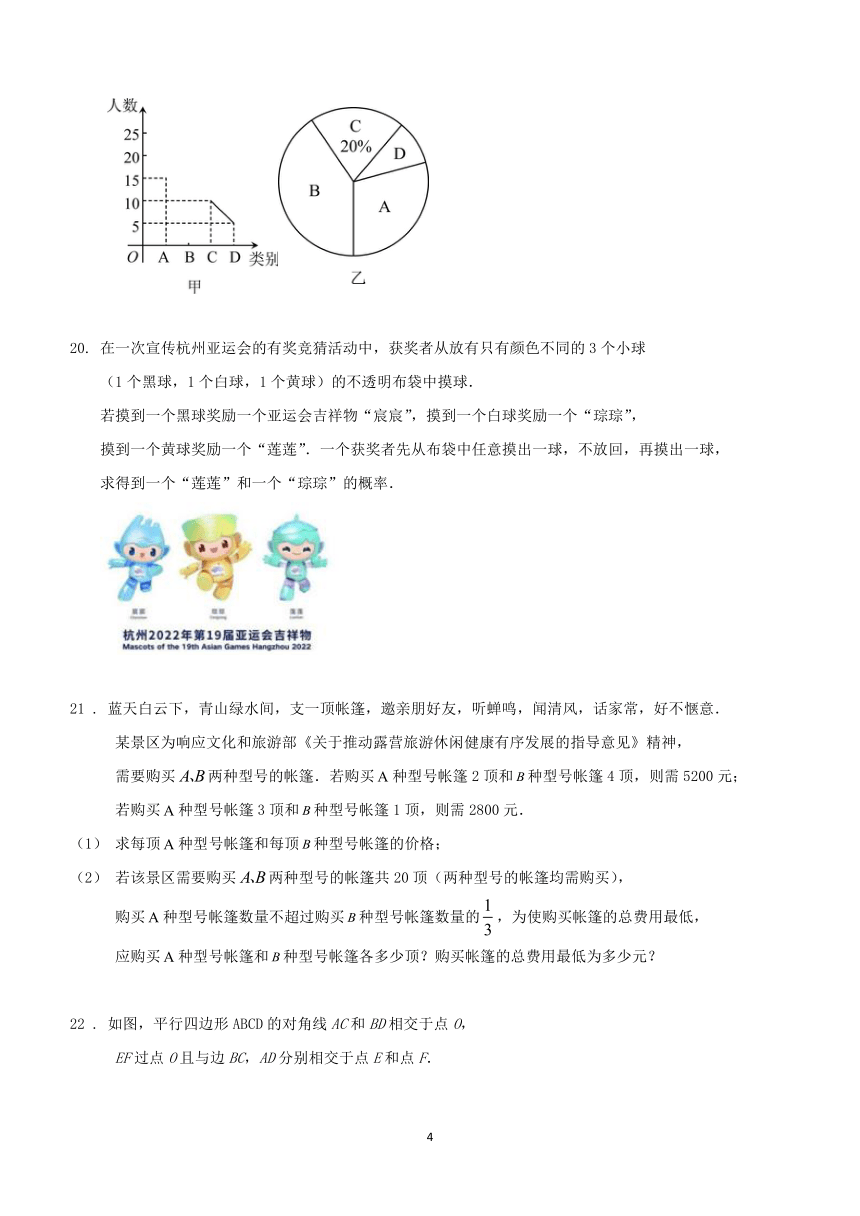
4月23日是世界读书日,学校学生发展中心在全校随机抽取了一部分学生,
对他们喜欢读的书进行统计,共归为四类:
A:历史类、B:文学类、C:科普类、D:艺术类,绘制出了两幅不完整的统计图,
请你根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)将图甲中的折线统计图补充完整;
(3)图乙中B类所占圆心角的度数为 ;
(4)若该校有3000名学生,请你估计选择“A:历史类”的学生约有 名.
20. 在一次宣传杭州亚运会的有奖竞猜活动中,获奖者从放有只有颜色不同的3个小球
(1个黑球,1个白球,1个黄球)的不透明布袋中摸球.
若摸到一个黑球奖励一个亚运会吉祥物“宸宸”,摸到一个白球奖励一个“琮琮”,
摸到一个黄球奖励一个“莲莲”.一个获奖者先从布袋中任意摸出一球,不放回,再摸出一球,
求得到一个“莲莲”和一个“琮琮”的概率.
21 . 蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.
某景区为响应文化和旅游部《关于推动露营旅游休闲健康有序发展的指导意见》精神,
需要购买两种型号的帐篷.若购买种型号帐篷2顶和种型号帐篷4顶,则需5200元;
若购买种型号帐篷3顶和种型号帐篷1顶,则需2800元.
求每顶种型号帐篷和每顶种型号帐篷的价格;
若该景区需要购买两种型号的帐篷共20顶(两种型号的帐篷均需购买),
购买种型号帐篷数量不超过购买种型号帐篷数量的,为使购买帐篷的总费用最低,
应购买种型号帐篷和种型号帐篷各多少顶?购买帐篷的总费用最低为多少元?
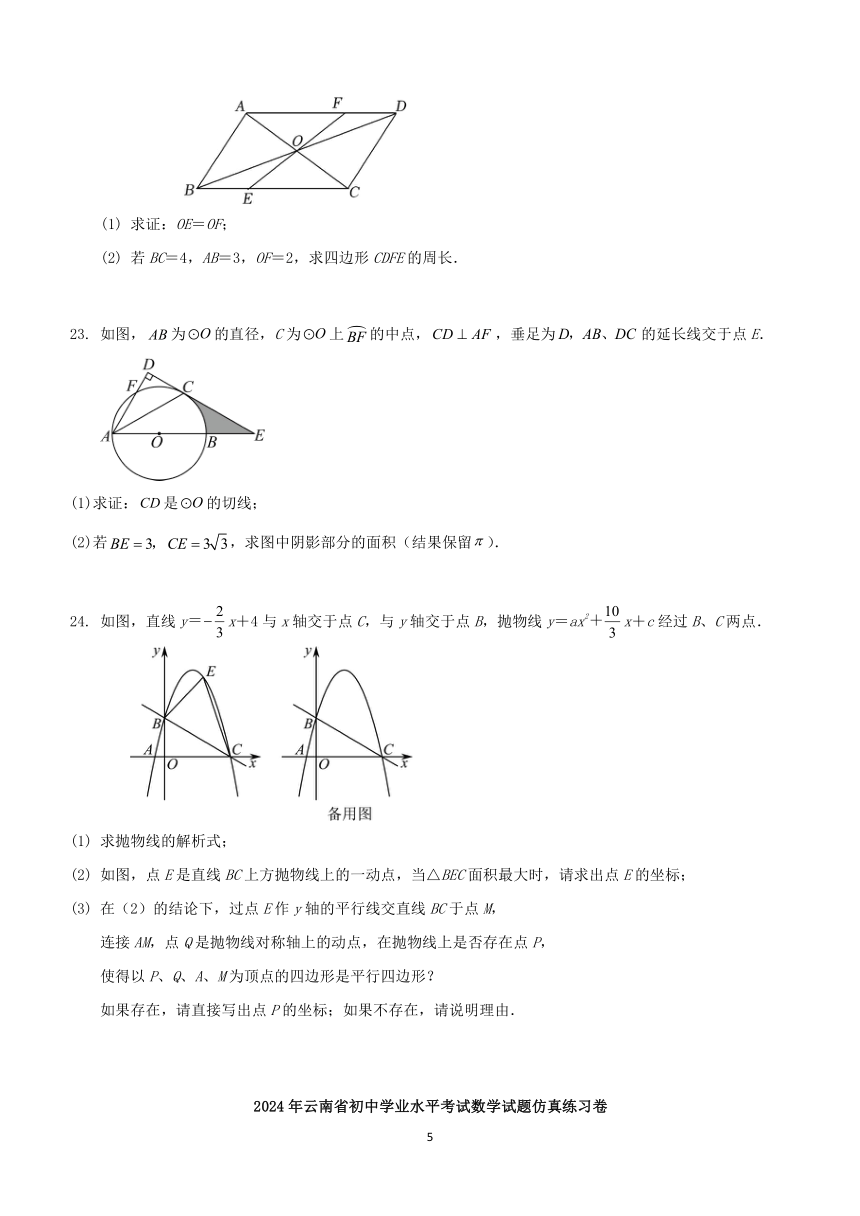
22 . 如图,平行四边形ABCD的对角线AC和BD相交于点O,
EF过点O且与边BC,AD分别相交于点E和点F.
求证:OE=OF;
若BC=4,AB=3,OF=2,求四边形CDFE的周长.
23. 如图,为的直径,C为上的中点,,垂足为的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
24. 如图,直线yx+4与x轴交于点C,与y轴交于点B,抛物线y=ax2x+c经过B、C两点.
求抛物线的解析式;
如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
在(2)的结论下,过点E作y轴的平行线交直线BC于点M,
连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,
使得以P、Q、A、M为顶点的四边形是平行四边形?
如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
2024年云南省初中学业水平考试数学试题仿真练习卷
答案解析
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,
则分别叫做正数与负数.如果收入100元记作元,那么元表示( )
A.支出80元 B.收入80元 C.支出100元 D.收入100元
【答案】A
【分析】根据正负数表示具有相反意义的量的表示方法即可完成.
【详解】根据题意,收入100元记作元,则元表示支出80元.
故选A.
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,
若∠1=60°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
【答案】A
【分析】本题先根据平行线的性质得到同位角相等,然后可求得∠2的度数.
【详解】如图:
∵直尺的两边互相平行,
∴∠3=∠1=60 (两直线平行,同位角相等),
∴∠2=90 -∠3=90 -60 =30 .
故选A.
3 . 第届亚运会将于年月日至月日在中国浙江省杭州市举行,
杭州奥体博览城游泳馆区建筑总面积平方米,将数用科学记数法表示为( )
A. B. C. D.
【答案】C
4 .如图所示的物体,其主视图是( )
A.B. C. D.
【答案】A
【分析】把从正面看到的平面图形画出来即可.
【详解】解:从正面可以看到的平面图形是
故选A
5. 下列计算正确的是( )
A. B. C. D.
【答案】C
【分析】分别根据同底数幂的乘法运算,合并同类项,积的乘方及完全平方公式进行计算,继而判断即可.
【详解】A.,因此该选项不符合题意;
B.与不是同类项,因此不能合并,所以该选项不符合题意;
C.,因此该选项符合题意;
D.,因此该选项不符合题意;
故选:C.
6. 某次数学测试共有5道题目,下面是901班30名同学的答对题数情况统计:
答对题数(道) 0 1 2 3 4 5
人数(人) 1 2 4 9 11 3
同学答对题数的众数和中位数分别是( )
A.4道,4道 B.11道,3道 C.4道,3道 D.11道,11道
【答案】C
【分析】根据众数:出现次数最多的数据,中位数:排序后中间一位或中间两位数据的平均数,进行求解即可.
【详解】解:有11人答对4道,数量最多,故众数为4道;
中位数为第15个和第16个数据的平均数:道;
故选C.
7. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B.且 C.且 D.
【答案】C
【分析】根据一元二次方程的定义结合根的判别式即可得出关于a的一元一次不等式组,解之即可得出结论.
【详解】解:∵关于x的一元二次方程有两个不相等的实数根,
,,
解得:且.
故选:C.
8. 已知、两点均在反比例函数的图象上,则的值为( )
A. B. C. D.
【答案】D
【分析】利用待定系数法求出反比例函数解析式,然后把代入反比例函数解析式,计算得出的值,即可得出答案.
【详解】解:把点的坐标代入,可得:,
解得:,
即,
把的坐标代入,可得:,
解得:.
故选:D
如图,两点被池塘隔开,三点不共线.设的中点分别为.
若米,则( )
A. 4米 B. 6米 C. 8米 D. 10米
【答案】B
【解析】
【分析】根据三角形中位线定理计算即可.
【详解】解∶∵的中点分别为,
∴是的中位线,
∴米,
故选∶B.
《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:
把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天:
如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.
设规定时间为天,则可列方程为( )
A. B. C. D.
【答案】A
【分析】根据快马、慢马所需时间及规定时间之间的关系,可得出慢马所需的时间为天,快马所需的时间为天,利用速度=路程÷时间,结合快马的速度是慢马的2倍,即可得出关于x的分式方程,此题得解.
【详解】解:规定时间为天,
慢马所需的时间为天,快马所需的时间为天,
又快马的速度是慢马的2倍,
可列出方程.
故选:A.
11. 如图,等边的三个顶点都在上,是的直径.若,则劣弧的长是( )
A. B. C. D.
【答案】B
【分析】连接OB,OC,根据圆周角定理得到∠BOC=2∠BAC,
证明△AOB≌△AOC,得到∠BAO=∠CAO=30°,得到∠BOD,再利用弧长公式计算.
【详解】解:连接OB,OC,
∵△ABC是等边三角形,
∴∠BOC=2∠BAC=120°,
又∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO=30°,
∴∠BOD=60°,
∴劣弧BD的长为=π,
故选B.
12 . 观察下列算式:,,,,,,,,…,
根据上述算式中的规律,你认为的末位数字是( )
A. B. C. D.
【答案】C
【分析】本题考查有理数的乘方及数字的变化规律—尾数特征,解题的关键是根据所给的式子,发现:(为正整数)的个位数字是,,,四个一循环,由,再根据规律即可得出答案.
【详解】解:∵,,,,,,,,…,
∴(为正整数)的个位数字是,,,四个一循环,
∵,
∴的末位数字与的末位数字相同,是.
故选:C.
二、填空题(本大题共4小题,每小题2分,共8分)
13. 在函数中,自变量x的取值范围是 .
【答案】
【详解】试题分析:求函数自变量的取值范围,就是求函数解析式有意义的条件,
根据二次根式被开方数必须是非负数的条件,
要使在实数范围内有意义,
必须.
14. 在直角中,,,,求为_______
【答案】
【解析】
【分析】根据锐角三角函数的概念和勾股定理求解,根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系及勾股定理,然后再代入三角函数进行求解,最后求出面积及的值.
【详解】解:由,,
得出:,
由勾股定理得出:,
.
故答案为:
15. 分解因式: .
【答案】
【分析】先提公因式,再利用平方差公式继续分解即可.
【详解】,
,
,
故答案为:
16. 如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
【答案】
【分析】延长FA交⊙A于G,如图所示:根据六边形ABCDEF是正六边形,AB=2,利用外角和求得∠GAB=,再求出正六边形内角∠FAB=180°-∠GAB=180°-60°=120°, 利用扇形面积公式代入数值计算即可.
【详解】解:延长FA交⊙A于G,如图所示:
∵六边形ABCDEF是正六边形,AB=2,
∴∠GAB=,
∠FAB=180°-∠GAB=180°-60°=120°,
∴,
故答案为.
三、解答题(本大题共8小题,共56分)
17. 计算:.
【答案】
【分析】原式分别利用乘方,特殊角的三角函数值,零指数幂,负整数指数幂,
乘法法则分别计算,再作加减法.
【详解】解:
=
=
18. 如图,点在一条直线上,,求证:.
【答案】见解析
【分析】根据题意,运用“边边边”的方法证明三角形全等.
【详解】证明:∵,
∴,即,
在和中
∴.
4月23日是世界读书日,学校学生发展中心在全校随机抽取了一部分学生,
对他们喜欢读的书进行统计,共归为四类:
A:历史类、B:文学类、C:科普类、D:艺术类,绘制出了两幅不完整的统计图,
请你根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)将图甲中的折线统计图补充完整;
(3)图乙中B类所占圆心角的度数为 ;
(4)若该校有3000名学生,请你估计选择“A:历史类”的学生约有 名.
【答案】(1)50;(2)见解析;(3)144°;(4)900
【分析】(1)根据C类的占比与人数即可求出抽取的总人数;
(2)求出B类的人数即可补全折线统计图;
(3)根据B类的人数即可求出其占比,进而可得结果;
(4)求出A类的占比即可求解.
【详解】(1)10÷20%=50
∴共抽取了50名学生进行调查;
故答案为:50;
(2)B类的人数为50-15-10-5=20(人)
故补全折线统计图如下:
(3)B类所占圆心角的度数为20÷50×360°=144°
故答案为:144°;
(4)该校有3000名学生,估计选择“A:历史类”的学生约有3000×=900(人)
故答案为:900.
20. 在一次宣传杭州亚运会的有奖竞猜活动中,获奖者从放有只有颜色不同的3个小球
(1个黑球,1个白球,1个黄球)的不透明布袋中摸球.
若摸到一个黑球奖励一个亚运会吉祥物“宸宸”,摸到一个白球奖励一个“琮琮”,
摸到一个黄球奖励一个“莲莲”.一个获奖者先从布袋中任意摸出一球,不放回,再摸出一球,
求得到一个“莲莲”和一个“琮琮”的概率.
【答案】
【分析】根据题意作图树状图,可知共有6种可能情况,而满足条件的有2种情况,进而求概率即可.
【详解】解:根据题意,可作树状图如下,
由树状图可知,共有6种可能情况,满足条件的有2种情况,
所以,得到一个“莲莲”和一个“琮琮”的概率为.
21 .蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.
某景区为响应文化和旅游部《关于推动露营旅游休闲健康有序发展的指导意见》精神,
需要购买两种型号的帐篷.若购买种型号帐篷2顶和种型号帐篷4顶,则需5200元;
若购买种型号帐篷3顶和种型号帐篷1顶,则需2800元.
(1)求每顶种型号帐篷和每顶种型号帐篷的价格;
(2)若该景区需要购买两种型号的帐篷共20顶(两种型号的帐篷均需购买),
购买种型号帐篷数量不超过购买种型号帐篷数量的,为使购买帐篷的总费用最低,
应购买种型号帐篷和种型号帐篷各多少顶?购买帐篷的总费用最低为多少元?
【答案】(1)每顶种型号帐篷的价格为600元,每顶种型号帐篷的价格为1000元
(2)当种型号帐篷为5顶时,种型号帐篷为15顶时,总费用最低,为18000元.
【解析】
【分析】(1)根据题意中的等量关系列出二元一次方程组,解出方程组后得到答案;
(2)根据购买种型号帐篷数量不超过购买种型号帐篷数量的,列出一元一次不等式,得出种型号帐篷数量范围,再根据一次函数的性质,取种型号帐篷数量的最大值时总费用最少,从而得出答案.
【小问1详解】
解:设每顶种型号帐篷的价格为元,每顶种型号帐篷的价格为元.
根据题意列方程组为:,
解得,
答:每顶种型号帐篷的价格为600元,每顶种型号帐篷的价格为1000元.
【小问2详解】
解:设种型号帐篷购买顶,总费用为元,则种型号帐篷为顶,
由题意得,
其中,得,
故当种型号帐篷为5顶时,总费用最低,总费用为,
答:当种型号帐篷为5顶时,种型号帐篷为15顶时,总费用最低,为18000元.
22 . 如图,平行四边形ABCD的对角线AC和BD相交于点O,
EF过点O且与边BC,AD分别相交于点E和点F.
(1)求证:OE=OF;
(2)若BC=4,AB=3,OF=2,求四边形CDFE的周长.
【答案】(1)证明见解析
(2)四边形CDFE的周长为11
【分析】(1)由四边形ABCD是平行四边形,可得OA=OC,,
继而可证得△AOE≌△COF(ASA),则可证得结论;
(2)由全等三角形的性质及平行四边形的性质可得出答案.
(1)
证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAF=∠OCE,
在△OAF和△OCE中,
,
∴△AOF≌△COE(ASA),
∴OF=OE;
(2)
解:∵△AOF≌△COE,
∴AF=CE,
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵BC=4,AB=3,OE=OF=2,
∴四边形CDFE的周长=EF+DF+CE+CD
=2OE+DF+AF+CD
=2OE+AD+CD
=4+4+3
=11.
23. 如图,为的直径,C为上的中点,,垂足为的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
【答案】(1)见解析
(2).
【分析】本题考查了切线的判定以及圆周角定理和扇形的面积公式.
(1)连接,利用半径相等、圆周角定理求得,推出,从而得到,即可证明是的切线;
(2)设半径为r,利用勾股定理得到,解得,再计算出,然后根据扇形的面积公式,利用进行计算即可.
【详解】(1)证明:连接,如图,
∵,
∴,
∵C为上的中点,即,
∴,
∴,
∴,
∵,
∴,
∵点C在上,
∴是的切线;
(2)解:连接,设半径为r,
在中,∵,
∴,
解得,
∴,
则,即点B是斜边的中点,
∴,
∴,
∴是等边三角形,
∴,
∴.
24. 如图,直线yx+4与x轴交于点C,与y轴交于点B,抛物线y=ax2x+c经过B、C两点.
求抛物线的解析式;
如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
在(2)的结论下,过点E作y轴的平行线交直线BC于点M,
连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,
使得以P、Q、A、M为顶点的四边形是平行四边形?
如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)yx2x+4
(2)E(3,8)
(3)存在,点P的坐标是(,)或(,)或(,)
【分析】(1)由一次函数的解析式可求出B点和C点坐标.再代入抛物线解析式中即可求出a和c的值,即得出抛物线解析式;
(2)过E作EG∥y轴,交直线BC于G,设E(m,m2m+4),则G(m,m+4),则可用m表示出EG的长,最后利用三角形面积公式即可求出S△BEC的值,再利用二次函数的性质即得出答案;
(3)根据二次函数解析式即得出其对称轴,由此可得出A点坐标.再由点Q是抛物线对称轴上的动点,得出Q的横坐标为.①当平行四边形以AM为边时,由题意可知点M的横坐标是3,再根据点M在直线yx+4上,即得出其纵坐标.再结合平行四边形的性质即得出平移规律,由此可得出P点坐标;②当平行四边形以AM为边时,同理可知点M的横坐标是3,Q的横坐标为,从而即得出P的坐标;③当平行四边形以AM为对角线时,由平行四边形的性质得出P到A的平移规律,即得出P点坐标.
【详解】(1)当x=0时,y=4,
∴B(0,4),
当y=0时,x+4=0,
解得:x=6,
∴C(6,0),
把B(0,4)和C(6,0)代入抛物线y=ax2x+c中得:
,
解得:,
∴抛物线的解析式为:yx2x+4;
(2)如图1,过E作EG∥y轴,交直线BC于G,
设E(m,m2m+4),则G(m,m+4),
∴EG=(m2m+4)﹣(m+4)4m,
∴S△BECEG OC6(4m)=﹣2(m﹣3)2+18,
∵﹣2<0,
∴S有最大值,此时E(3,8);
(3)yx2x+4(x)2;
∴该抛物线对称轴是:x,
∴A(-1,0)
∵点Q是抛物线对称轴上的动点,
∴Q的横坐标为,
在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形;
①如图2,以AM为边时,
由(2),可得点M的横坐标是3,
∵点M在直线yx+4上,
∴点M的坐标是(3,2),
又∵点A的坐标是(-1,0),点Q的横坐标为,
根据M到Q的平移规律:可知:P的横坐标为,
∴P(,);
②如图3,以AM为边时,
∵由(2),可得点M的横坐标是3,
∵A(-1,0),且Q的横坐标为,
∴P的横坐标为,
∴P(,);
③以AM为对角线时,如图4,
∵M到Q的平移规律可得P到A的平移规律,
∴点P的坐标是(,),
综上所述,在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,
点P的坐标是(,)或(,)或(,).
(全卷三个大题,共24个小题,共8页;满分100分,考试用时120分钟)
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,
则分别叫做正数与负数.如果收入100元记作元,那么元表示( )
A.支出80元 B.收入80元 C.支出100元 D.收入100元
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,
若∠1=60°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
3 . 第届亚运会将于年月日至月日在中国浙江省杭州市举行,
杭州奥体博览城游泳馆区建筑总面积平方米,将数用科学记数法表示为( )
A. B. C. D.
4 .如图所示的物体,其主视图是( )
A.B. C. D.
5. 下列计算正确的是( )
A. B. C. D.
6. 某次数学测试共有5道题目,下面是901班30名同学的答对题数情况统计:
答对题数(道) 0 1 2 3 4 5
人数(人) 1 2 4 9 11 3
同学答对题数的众数和中位数分别是( )
A.4道,4道 B.11道,3道 C.4道,3道 D.11道,11道
7. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B.且 C.且 D.
8. 已知、两点均在反比例函数的图象上,则的值为( )
A. B. C. D.
如图,两点被池塘隔开,三点不共线.设的中点分别为.
若米,则( )
A. 4米 B. 6米 C. 8米 D. 10米
《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:
把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天:
如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.
设规定时间为天,则可列方程为( )
A. B. C. D.
11. 如图,等边的三个顶点都在上,是的直径.若,则劣弧的长是( )
A. B. C. D.
12 . 观察下列算式:,,,,,,,,…,
根据上述算式中的规律,你认为的末位数字是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题2分,共8分)
13. 在函数中,自变量x的取值范围是 .
14. 在直角中,,,,求为_______
15. 分解因式: .
16. 如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
三、解答题(本大题共8小题,共56分)
17. 计算:.
18. 如图,点在一条直线上,,求证:.
4月23日是世界读书日,学校学生发展中心在全校随机抽取了一部分学生,
对他们喜欢读的书进行统计,共归为四类:
A:历史类、B:文学类、C:科普类、D:艺术类,绘制出了两幅不完整的统计图,
请你根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)将图甲中的折线统计图补充完整;
(3)图乙中B类所占圆心角的度数为 ;
(4)若该校有3000名学生,请你估计选择“A:历史类”的学生约有 名.
20. 在一次宣传杭州亚运会的有奖竞猜活动中,获奖者从放有只有颜色不同的3个小球
(1个黑球,1个白球,1个黄球)的不透明布袋中摸球.
若摸到一个黑球奖励一个亚运会吉祥物“宸宸”,摸到一个白球奖励一个“琮琮”,
摸到一个黄球奖励一个“莲莲”.一个获奖者先从布袋中任意摸出一球,不放回,再摸出一球,
求得到一个“莲莲”和一个“琮琮”的概率.
21 . 蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.
某景区为响应文化和旅游部《关于推动露营旅游休闲健康有序发展的指导意见》精神,
需要购买两种型号的帐篷.若购买种型号帐篷2顶和种型号帐篷4顶,则需5200元;
若购买种型号帐篷3顶和种型号帐篷1顶,则需2800元.
求每顶种型号帐篷和每顶种型号帐篷的价格;
若该景区需要购买两种型号的帐篷共20顶(两种型号的帐篷均需购买),
购买种型号帐篷数量不超过购买种型号帐篷数量的,为使购买帐篷的总费用最低,
应购买种型号帐篷和种型号帐篷各多少顶?购买帐篷的总费用最低为多少元?
22 . 如图,平行四边形ABCD的对角线AC和BD相交于点O,
EF过点O且与边BC,AD分别相交于点E和点F.
求证:OE=OF;
若BC=4,AB=3,OF=2,求四边形CDFE的周长.
23. 如图,为的直径,C为上的中点,,垂足为的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
24. 如图,直线yx+4与x轴交于点C,与y轴交于点B,抛物线y=ax2x+c经过B、C两点.
求抛物线的解析式;
如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
在(2)的结论下,过点E作y轴的平行线交直线BC于点M,
连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,
使得以P、Q、A、M为顶点的四边形是平行四边形?
如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
2024年云南省初中学业水平考试数学试题仿真练习卷
答案解析
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,
则分别叫做正数与负数.如果收入100元记作元,那么元表示( )
A.支出80元 B.收入80元 C.支出100元 D.收入100元
【答案】A
【分析】根据正负数表示具有相反意义的量的表示方法即可完成.
【详解】根据题意,收入100元记作元,则元表示支出80元.
故选A.
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,
若∠1=60°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
【答案】A
【分析】本题先根据平行线的性质得到同位角相等,然后可求得∠2的度数.
【详解】如图:
∵直尺的两边互相平行,
∴∠3=∠1=60 (两直线平行,同位角相等),
∴∠2=90 -∠3=90 -60 =30 .
故选A.
3 . 第届亚运会将于年月日至月日在中国浙江省杭州市举行,
杭州奥体博览城游泳馆区建筑总面积平方米,将数用科学记数法表示为( )
A. B. C. D.
【答案】C
4 .如图所示的物体,其主视图是( )
A.B. C. D.
【答案】A
【分析】把从正面看到的平面图形画出来即可.
【详解】解:从正面可以看到的平面图形是
故选A
5. 下列计算正确的是( )
A. B. C. D.
【答案】C
【分析】分别根据同底数幂的乘法运算,合并同类项,积的乘方及完全平方公式进行计算,继而判断即可.
【详解】A.,因此该选项不符合题意;
B.与不是同类项,因此不能合并,所以该选项不符合题意;
C.,因此该选项符合题意;
D.,因此该选项不符合题意;
故选:C.
6. 某次数学测试共有5道题目,下面是901班30名同学的答对题数情况统计:
答对题数(道) 0 1 2 3 4 5
人数(人) 1 2 4 9 11 3
同学答对题数的众数和中位数分别是( )
A.4道,4道 B.11道,3道 C.4道,3道 D.11道,11道
【答案】C
【分析】根据众数:出现次数最多的数据,中位数:排序后中间一位或中间两位数据的平均数,进行求解即可.
【详解】解:有11人答对4道,数量最多,故众数为4道;
中位数为第15个和第16个数据的平均数:道;
故选C.
7. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B.且 C.且 D.
【答案】C
【分析】根据一元二次方程的定义结合根的判别式即可得出关于a的一元一次不等式组,解之即可得出结论.
【详解】解:∵关于x的一元二次方程有两个不相等的实数根,
,,
解得:且.
故选:C.
8. 已知、两点均在反比例函数的图象上,则的值为( )
A. B. C. D.
【答案】D
【分析】利用待定系数法求出反比例函数解析式,然后把代入反比例函数解析式,计算得出的值,即可得出答案.
【详解】解:把点的坐标代入,可得:,
解得:,
即,
把的坐标代入,可得:,
解得:.
故选:D
如图,两点被池塘隔开,三点不共线.设的中点分别为.
若米,则( )
A. 4米 B. 6米 C. 8米 D. 10米
【答案】B
【解析】
【分析】根据三角形中位线定理计算即可.
【详解】解∶∵的中点分别为,
∴是的中位线,
∴米,
故选∶B.
《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:
把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天:
如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.
设规定时间为天,则可列方程为( )
A. B. C. D.
【答案】A
【分析】根据快马、慢马所需时间及规定时间之间的关系,可得出慢马所需的时间为天,快马所需的时间为天,利用速度=路程÷时间,结合快马的速度是慢马的2倍,即可得出关于x的分式方程,此题得解.
【详解】解:规定时间为天,
慢马所需的时间为天,快马所需的时间为天,
又快马的速度是慢马的2倍,
可列出方程.
故选:A.
11. 如图,等边的三个顶点都在上,是的直径.若,则劣弧的长是( )
A. B. C. D.
【答案】B
【分析】连接OB,OC,根据圆周角定理得到∠BOC=2∠BAC,
证明△AOB≌△AOC,得到∠BAO=∠CAO=30°,得到∠BOD,再利用弧长公式计算.
【详解】解:连接OB,OC,
∵△ABC是等边三角形,
∴∠BOC=2∠BAC=120°,
又∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO=30°,
∴∠BOD=60°,
∴劣弧BD的长为=π,
故选B.
12 . 观察下列算式:,,,,,,,,…,
根据上述算式中的规律,你认为的末位数字是( )
A. B. C. D.
【答案】C
【分析】本题考查有理数的乘方及数字的变化规律—尾数特征,解题的关键是根据所给的式子,发现:(为正整数)的个位数字是,,,四个一循环,由,再根据规律即可得出答案.
【详解】解:∵,,,,,,,,…,
∴(为正整数)的个位数字是,,,四个一循环,
∵,
∴的末位数字与的末位数字相同,是.
故选:C.
二、填空题(本大题共4小题,每小题2分,共8分)
13. 在函数中,自变量x的取值范围是 .
【答案】
【详解】试题分析:求函数自变量的取值范围,就是求函数解析式有意义的条件,
根据二次根式被开方数必须是非负数的条件,
要使在实数范围内有意义,
必须.
14. 在直角中,,,,求为_______
【答案】
【解析】
【分析】根据锐角三角函数的概念和勾股定理求解,根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系及勾股定理,然后再代入三角函数进行求解,最后求出面积及的值.
【详解】解:由,,
得出:,
由勾股定理得出:,
.
故答案为:
15. 分解因式: .
【答案】
【分析】先提公因式,再利用平方差公式继续分解即可.
【详解】,
,
,
故答案为:
16. 如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
【答案】
【分析】延长FA交⊙A于G,如图所示:根据六边形ABCDEF是正六边形,AB=2,利用外角和求得∠GAB=,再求出正六边形内角∠FAB=180°-∠GAB=180°-60°=120°, 利用扇形面积公式代入数值计算即可.
【详解】解:延长FA交⊙A于G,如图所示:
∵六边形ABCDEF是正六边形,AB=2,
∴∠GAB=,
∠FAB=180°-∠GAB=180°-60°=120°,
∴,
故答案为.
三、解答题(本大题共8小题,共56分)
17. 计算:.
【答案】
【分析】原式分别利用乘方,特殊角的三角函数值,零指数幂,负整数指数幂,
乘法法则分别计算,再作加减法.
【详解】解:
=
=
18. 如图,点在一条直线上,,求证:.
【答案】见解析
【分析】根据题意,运用“边边边”的方法证明三角形全等.
【详解】证明:∵,
∴,即,
在和中
∴.
4月23日是世界读书日,学校学生发展中心在全校随机抽取了一部分学生,
对他们喜欢读的书进行统计,共归为四类:
A:历史类、B:文学类、C:科普类、D:艺术类,绘制出了两幅不完整的统计图,
请你根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)将图甲中的折线统计图补充完整;
(3)图乙中B类所占圆心角的度数为 ;
(4)若该校有3000名学生,请你估计选择“A:历史类”的学生约有 名.
【答案】(1)50;(2)见解析;(3)144°;(4)900
【分析】(1)根据C类的占比与人数即可求出抽取的总人数;
(2)求出B类的人数即可补全折线统计图;
(3)根据B类的人数即可求出其占比,进而可得结果;
(4)求出A类的占比即可求解.
【详解】(1)10÷20%=50
∴共抽取了50名学生进行调查;
故答案为:50;
(2)B类的人数为50-15-10-5=20(人)
故补全折线统计图如下:
(3)B类所占圆心角的度数为20÷50×360°=144°
故答案为:144°;
(4)该校有3000名学生,估计选择“A:历史类”的学生约有3000×=900(人)
故答案为:900.
20. 在一次宣传杭州亚运会的有奖竞猜活动中,获奖者从放有只有颜色不同的3个小球
(1个黑球,1个白球,1个黄球)的不透明布袋中摸球.
若摸到一个黑球奖励一个亚运会吉祥物“宸宸”,摸到一个白球奖励一个“琮琮”,
摸到一个黄球奖励一个“莲莲”.一个获奖者先从布袋中任意摸出一球,不放回,再摸出一球,
求得到一个“莲莲”和一个“琮琮”的概率.
【答案】
【分析】根据题意作图树状图,可知共有6种可能情况,而满足条件的有2种情况,进而求概率即可.
【详解】解:根据题意,可作树状图如下,
由树状图可知,共有6种可能情况,满足条件的有2种情况,
所以,得到一个“莲莲”和一个“琮琮”的概率为.
21 .蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.
某景区为响应文化和旅游部《关于推动露营旅游休闲健康有序发展的指导意见》精神,
需要购买两种型号的帐篷.若购买种型号帐篷2顶和种型号帐篷4顶,则需5200元;
若购买种型号帐篷3顶和种型号帐篷1顶,则需2800元.
(1)求每顶种型号帐篷和每顶种型号帐篷的价格;
(2)若该景区需要购买两种型号的帐篷共20顶(两种型号的帐篷均需购买),
购买种型号帐篷数量不超过购买种型号帐篷数量的,为使购买帐篷的总费用最低,
应购买种型号帐篷和种型号帐篷各多少顶?购买帐篷的总费用最低为多少元?
【答案】(1)每顶种型号帐篷的价格为600元,每顶种型号帐篷的价格为1000元
(2)当种型号帐篷为5顶时,种型号帐篷为15顶时,总费用最低,为18000元.
【解析】
【分析】(1)根据题意中的等量关系列出二元一次方程组,解出方程组后得到答案;
(2)根据购买种型号帐篷数量不超过购买种型号帐篷数量的,列出一元一次不等式,得出种型号帐篷数量范围,再根据一次函数的性质,取种型号帐篷数量的最大值时总费用最少,从而得出答案.
【小问1详解】
解:设每顶种型号帐篷的价格为元,每顶种型号帐篷的价格为元.
根据题意列方程组为:,
解得,
答:每顶种型号帐篷的价格为600元,每顶种型号帐篷的价格为1000元.
【小问2详解】
解:设种型号帐篷购买顶,总费用为元,则种型号帐篷为顶,
由题意得,
其中,得,
故当种型号帐篷为5顶时,总费用最低,总费用为,
答:当种型号帐篷为5顶时,种型号帐篷为15顶时,总费用最低,为18000元.
22 . 如图,平行四边形ABCD的对角线AC和BD相交于点O,
EF过点O且与边BC,AD分别相交于点E和点F.
(1)求证:OE=OF;
(2)若BC=4,AB=3,OF=2,求四边形CDFE的周长.
【答案】(1)证明见解析
(2)四边形CDFE的周长为11
【分析】(1)由四边形ABCD是平行四边形,可得OA=OC,,
继而可证得△AOE≌△COF(ASA),则可证得结论;
(2)由全等三角形的性质及平行四边形的性质可得出答案.
(1)
证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAF=∠OCE,
在△OAF和△OCE中,
,
∴△AOF≌△COE(ASA),
∴OF=OE;
(2)
解:∵△AOF≌△COE,
∴AF=CE,
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵BC=4,AB=3,OE=OF=2,
∴四边形CDFE的周长=EF+DF+CE+CD
=2OE+DF+AF+CD
=2OE+AD+CD
=4+4+3
=11.
23. 如图,为的直径,C为上的中点,,垂足为的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
【答案】(1)见解析
(2).
【分析】本题考查了切线的判定以及圆周角定理和扇形的面积公式.
(1)连接,利用半径相等、圆周角定理求得,推出,从而得到,即可证明是的切线;
(2)设半径为r,利用勾股定理得到,解得,再计算出,然后根据扇形的面积公式,利用进行计算即可.
【详解】(1)证明:连接,如图,
∵,
∴,
∵C为上的中点,即,
∴,
∴,
∴,
∵,
∴,
∵点C在上,
∴是的切线;
(2)解:连接,设半径为r,
在中,∵,
∴,
解得,
∴,
则,即点B是斜边的中点,
∴,
∴,
∴是等边三角形,
∴,
∴.
24. 如图,直线yx+4与x轴交于点C,与y轴交于点B,抛物线y=ax2x+c经过B、C两点.
求抛物线的解析式;
如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
在(2)的结论下,过点E作y轴的平行线交直线BC于点M,
连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,
使得以P、Q、A、M为顶点的四边形是平行四边形?
如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)yx2x+4
(2)E(3,8)
(3)存在,点P的坐标是(,)或(,)或(,)
【分析】(1)由一次函数的解析式可求出B点和C点坐标.再代入抛物线解析式中即可求出a和c的值,即得出抛物线解析式;
(2)过E作EG∥y轴,交直线BC于G,设E(m,m2m+4),则G(m,m+4),则可用m表示出EG的长,最后利用三角形面积公式即可求出S△BEC的值,再利用二次函数的性质即得出答案;
(3)根据二次函数解析式即得出其对称轴,由此可得出A点坐标.再由点Q是抛物线对称轴上的动点,得出Q的横坐标为.①当平行四边形以AM为边时,由题意可知点M的横坐标是3,再根据点M在直线yx+4上,即得出其纵坐标.再结合平行四边形的性质即得出平移规律,由此可得出P点坐标;②当平行四边形以AM为边时,同理可知点M的横坐标是3,Q的横坐标为,从而即得出P的坐标;③当平行四边形以AM为对角线时,由平行四边形的性质得出P到A的平移规律,即得出P点坐标.
【详解】(1)当x=0时,y=4,
∴B(0,4),
当y=0时,x+4=0,
解得:x=6,
∴C(6,0),
把B(0,4)和C(6,0)代入抛物线y=ax2x+c中得:
,
解得:,
∴抛物线的解析式为:yx2x+4;
(2)如图1,过E作EG∥y轴,交直线BC于G,
设E(m,m2m+4),则G(m,m+4),
∴EG=(m2m+4)﹣(m+4)4m,
∴S△BECEG OC6(4m)=﹣2(m﹣3)2+18,
∵﹣2<0,
∴S有最大值,此时E(3,8);
(3)yx2x+4(x)2;
∴该抛物线对称轴是:x,
∴A(-1,0)
∵点Q是抛物线对称轴上的动点,
∴Q的横坐标为,
在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形;
①如图2,以AM为边时,
由(2),可得点M的横坐标是3,
∵点M在直线yx+4上,
∴点M的坐标是(3,2),
又∵点A的坐标是(-1,0),点Q的横坐标为,
根据M到Q的平移规律:可知:P的横坐标为,
∴P(,);
②如图3,以AM为边时,
∵由(2),可得点M的横坐标是3,
∵A(-1,0),且Q的横坐标为,
∴P的横坐标为,
∴P(,);
③以AM为对角线时,如图4,
∵M到Q的平移规律可得P到A的平移规律,
∴点P的坐标是(,),
综上所述,在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,
点P的坐标是(,)或(,)或(,).
同课章节目录
