6.1.3 众数 课件(共24张PPT)
文档属性
| 名称 | 6.1.3 众数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-06 18:37:16 | ||
图片预览







文档简介
(共24张PPT)
6.1.3 众 数
1.在现实情景中认识众数的意义及优、缺点.
2.在具体情景中运用众数处理一些实际问题.
3.让学生经历运用众数描述数量信息的过程,调动学生学习的积极性,发展学生的数据统计概念.
4.体验众数与日常生活的密切联系,体会统计在生活中的广泛应用,从而明确学习目的,培养学习的兴趣.
【教学重点】理解众数的意义并会求一组数据的众数.
【教学难点】区别一组数据的平均数、众数、中位数.
(1)中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据;
(2)求中位数时,先将数据按一定的顺序排列,若这组数据是奇数个,则中间的数据是中位数;若这组数据是偶数个时,则中间的两个数据的平均数是中位数;
中位数的意义:中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数,因此,在一定
意义上中位数代表了一组数据的“中点”。
做一做:有 6 户家庭的年收入分别为(单位:万元):4,5,5,6,7,50.你认为这 6 户家庭的年收入水平大概是多少?
(1) 用平均数估计: (万元).
(2) 用中位数估计:中位数是 (万元).
如果把数据 50 改成 9,结果又会怎样?
还可用什么来刻画数据的特性呢?
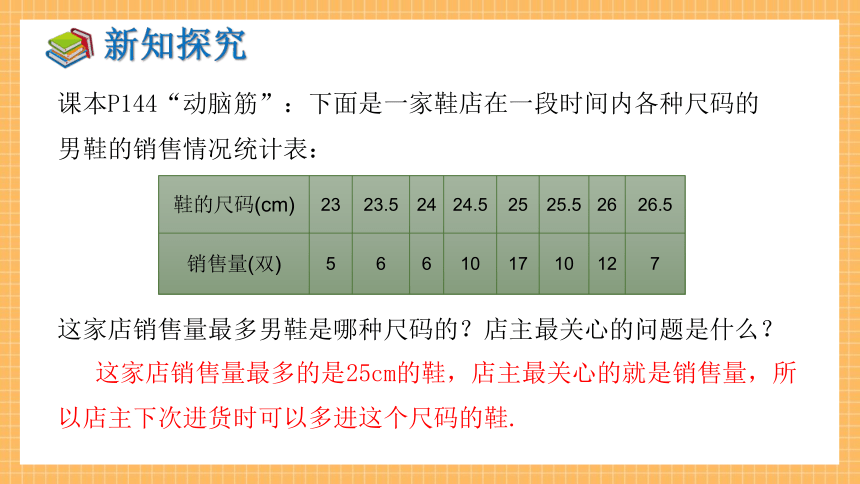
课本P144“动脑筋”:下面是一家鞋店在一段时间内各种尺码的男鞋的销售情况统计表:
这家店销售量最多男鞋是哪种尺码的?店主最关心的问题是什么?
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
这家店销售量最多的是25cm的鞋,店主最关心的就是销售量,所以店主下次进货时可以多进这个尺码的鞋.
注意:
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个,如 1,1,2,3,3,5 中众数是 1 和 3;
(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如 1,1,1,2,2,5 中众数是 1 而不是 3.
一组数据中出现次数最多的数称为这组数据的众数.
【例4】某公司全体职工的月工资如下:
试求出该公司月工资数据中的众数、中位数和平均数.
这组数据的众数是5000.
这组数据的中位数是(5000+5500)÷2=5250.
这组数据的平均数为
x=(21000+15000×2+11000×3+9000×4+7000×10+5500×20
+5000×22+4500×12+4200×6)÷80=489200÷80=6115.
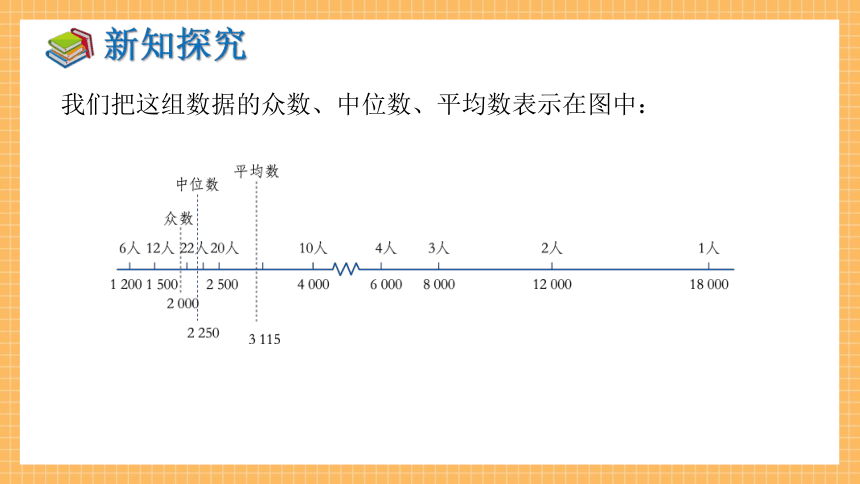
我们把这组数据的众数、中位数、平均数表示在图中:
工资的平均数6115偏高,因为大多数员工的工资都达不到这个平均数,用它来作为该公司员工工资的代表值并不合适.
众数是5000,中位数是5250,它们代表了大多数人的工资水平,不偏高也不偏低,较能反映工资水平的实际情况.
4200
4500
5500
7000
9000
11000
15000
21000
6人
12人
20人
10人
4人
3人
2人
1人
5000
众数
5250
中位数
6115
平均数
在例4中,你认为用平均数、中位数或众数中的哪一个更能反映该公司的工资水平?
公司总经理最关心的是公司月工资的总额,所以他关注的是平均数.
普通员工关注的是自己的收入在本公司职工群体中的位置,中位数能帮助职工了解自己的工资收入是“中上”还是“中下”水平……
在例中,对于职工月工资数据的平均数、中位数和众数,你认为该公司总经理、普通员工及应聘者将分别关注哪一个?说说你的理由, 并相互交流.
应聘者关注的是该公司月工资的众数,因为应聘者最想知道的是公司发给大多数员工的工资数,这也是一般的应聘者将会拿到的工资.
平均数、中位数和众数都是一组数据的代表,它们从不同侧面反映了数据的集中趋势.
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,因此在现实生活中应用较广,但它容易受极端值的影响;
中位数对极端值不敏感,但没有利用数据中所有的信息;
众数只能反映一组数据中出现次数最多的数据,也没有利用数据中所有的信息.
1、八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
他们都认为自己的数学成绩比其他两位同学好, 你能说说他们的依据是什么吗?
分析:小华成绩的众数是_____,中位数是_____,
平均数是_____;小明成绩的众数是_____,中位数是____,平均数是_____;小丽成绩的众数是____,中位数是____,平均数是____.
98
62
95
98
89.4
84.2
99
85
77
因为在他们的成绩之中,小华的平均数最大,小明的中位数最大,小丽的众数最大,所以都有理由认为自己的成绩比其他两位同学好.
2、甲、乙两名运动员在 6 次百米跑训练中的成绩如下:
甲(秒) 10.8 10.9 11.0 10.7 11.2 10.8
乙(秒) 10.9 10.9 10.8 10.8 10.5 10.9
请你比较这两组数据的众数,平均数和中位数,再谈谈你的看法.
分析:谈看法实质上就是按众数,平均数和中位数的大小比较其优劣.
解:甲:平均数是 10.9,众数是 10.8,中位数是 10.85;
乙:平均数是 10.8,众数是 10.9,中位数是 10.85.
从平均数看,甲的成绩比乙的好;从众数看,乙的成绩比甲的好;从中位数看两人成绩一样.
1、数据3,8,8,5,7,5,7,5,7的众数是( )
2、数据80,70,95,80,70,70,85,80,60,75的众数是( )
3、若五个正整数的中位数是3,唯一的众数是7,则这五个数的平均数是( )。
70和80
7
4
4. 根据实际情况填写(填平均数、中位数、众数):
① 老板进货时更关注卖出商品的 ;
② 评委给选手综合得分时更关注 ;
③ 普通在职员工更关注公司员工工资的 .
中位数
平均数
众数
5、一组数据:-1,1,3,4,a,若它们的平均数为2,则这组数据的众数为( )
6、若一组数据1,2,3,x,1,3,2有唯一的众数2,则这组数据的平均数是( ),中位数是( ).
3
2
2
7. 某校有 25 名同学参加某比赛,预赛成绩各不相同,取前 13 名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这 25 名同学成绩的 ( )
A. 最高分 B. 中位数 C. 众数 D. 平均数
B
8.某班30人所穿运动服尺码的情况为:穿75号码的有5人,穿80号码的有6人,穿85号码的有15人,穿90号码的有3人,穿95号码的有1人.穿哪一种尺码衣服的人最多?这个数据称为什么数?
答:穿85号码的人最多,这个数据称为众数.
9. 公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,16,17,17.
乙群:3,4,4,5,5,6,6,54,57.
(1)甲群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映甲群游客年龄特征的是 ;
(2)乙群游客的平均年龄是 岁,中位数是 岁,众数是 岁.其中能较好反映乙群游客年龄特征的是 .
众数
定义:出现次数最多的数
平均数、中位数、众数的意义:平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”
1. 习题6.1中第5、6、7题.
2.完成同步练习册中本课时的练习.
6.1.3 众 数
1.在现实情景中认识众数的意义及优、缺点.
2.在具体情景中运用众数处理一些实际问题.
3.让学生经历运用众数描述数量信息的过程,调动学生学习的积极性,发展学生的数据统计概念.
4.体验众数与日常生活的密切联系,体会统计在生活中的广泛应用,从而明确学习目的,培养学习的兴趣.
【教学重点】理解众数的意义并会求一组数据的众数.
【教学难点】区别一组数据的平均数、众数、中位数.
(1)中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据;
(2)求中位数时,先将数据按一定的顺序排列,若这组数据是奇数个,则中间的数据是中位数;若这组数据是偶数个时,则中间的两个数据的平均数是中位数;
中位数的意义:中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数,因此,在一定
意义上中位数代表了一组数据的“中点”。
做一做:有 6 户家庭的年收入分别为(单位:万元):4,5,5,6,7,50.你认为这 6 户家庭的年收入水平大概是多少?
(1) 用平均数估计: (万元).
(2) 用中位数估计:中位数是 (万元).
如果把数据 50 改成 9,结果又会怎样?
还可用什么来刻画数据的特性呢?
课本P144“动脑筋”:下面是一家鞋店在一段时间内各种尺码的男鞋的销售情况统计表:
这家店销售量最多男鞋是哪种尺码的?店主最关心的问题是什么?
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
这家店销售量最多的是25cm的鞋,店主最关心的就是销售量,所以店主下次进货时可以多进这个尺码的鞋.
注意:
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个,如 1,1,2,3,3,5 中众数是 1 和 3;
(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如 1,1,1,2,2,5 中众数是 1 而不是 3.
一组数据中出现次数最多的数称为这组数据的众数.
【例4】某公司全体职工的月工资如下:
试求出该公司月工资数据中的众数、中位数和平均数.
这组数据的众数是5000.
这组数据的中位数是(5000+5500)÷2=5250.
这组数据的平均数为
x=(21000+15000×2+11000×3+9000×4+7000×10+5500×20
+5000×22+4500×12+4200×6)÷80=489200÷80=6115.
我们把这组数据的众数、中位数、平均数表示在图中:
工资的平均数6115偏高,因为大多数员工的工资都达不到这个平均数,用它来作为该公司员工工资的代表值并不合适.
众数是5000,中位数是5250,它们代表了大多数人的工资水平,不偏高也不偏低,较能反映工资水平的实际情况.
4200
4500
5500
7000
9000
11000
15000
21000
6人
12人
20人
10人
4人
3人
2人
1人
5000
众数
5250
中位数
6115
平均数
在例4中,你认为用平均数、中位数或众数中的哪一个更能反映该公司的工资水平?
公司总经理最关心的是公司月工资的总额,所以他关注的是平均数.
普通员工关注的是自己的收入在本公司职工群体中的位置,中位数能帮助职工了解自己的工资收入是“中上”还是“中下”水平……
在例中,对于职工月工资数据的平均数、中位数和众数,你认为该公司总经理、普通员工及应聘者将分别关注哪一个?说说你的理由, 并相互交流.
应聘者关注的是该公司月工资的众数,因为应聘者最想知道的是公司发给大多数员工的工资数,这也是一般的应聘者将会拿到的工资.
平均数、中位数和众数都是一组数据的代表,它们从不同侧面反映了数据的集中趋势.
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,因此在现实生活中应用较广,但它容易受极端值的影响;
中位数对极端值不敏感,但没有利用数据中所有的信息;
众数只能反映一组数据中出现次数最多的数据,也没有利用数据中所有的信息.
1、八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
他们都认为自己的数学成绩比其他两位同学好, 你能说说他们的依据是什么吗?
分析:小华成绩的众数是_____,中位数是_____,
平均数是_____;小明成绩的众数是_____,中位数是____,平均数是_____;小丽成绩的众数是____,中位数是____,平均数是____.
98
62
95
98
89.4
84.2
99
85
77
因为在他们的成绩之中,小华的平均数最大,小明的中位数最大,小丽的众数最大,所以都有理由认为自己的成绩比其他两位同学好.
2、甲、乙两名运动员在 6 次百米跑训练中的成绩如下:
甲(秒) 10.8 10.9 11.0 10.7 11.2 10.8
乙(秒) 10.9 10.9 10.8 10.8 10.5 10.9
请你比较这两组数据的众数,平均数和中位数,再谈谈你的看法.
分析:谈看法实质上就是按众数,平均数和中位数的大小比较其优劣.
解:甲:平均数是 10.9,众数是 10.8,中位数是 10.85;
乙:平均数是 10.8,众数是 10.9,中位数是 10.85.
从平均数看,甲的成绩比乙的好;从众数看,乙的成绩比甲的好;从中位数看两人成绩一样.
1、数据3,8,8,5,7,5,7,5,7的众数是( )
2、数据80,70,95,80,70,70,85,80,60,75的众数是( )
3、若五个正整数的中位数是3,唯一的众数是7,则这五个数的平均数是( )。
70和80
7
4
4. 根据实际情况填写(填平均数、中位数、众数):
① 老板进货时更关注卖出商品的 ;
② 评委给选手综合得分时更关注 ;
③ 普通在职员工更关注公司员工工资的 .
中位数
平均数
众数
5、一组数据:-1,1,3,4,a,若它们的平均数为2,则这组数据的众数为( )
6、若一组数据1,2,3,x,1,3,2有唯一的众数2,则这组数据的平均数是( ),中位数是( ).
3
2
2
7. 某校有 25 名同学参加某比赛,预赛成绩各不相同,取前 13 名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这 25 名同学成绩的 ( )
A. 最高分 B. 中位数 C. 众数 D. 平均数
B
8.某班30人所穿运动服尺码的情况为:穿75号码的有5人,穿80号码的有6人,穿85号码的有15人,穿90号码的有3人,穿95号码的有1人.穿哪一种尺码衣服的人最多?这个数据称为什么数?
答:穿85号码的人最多,这个数据称为众数.
9. 公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,16,17,17.
乙群:3,4,4,5,5,6,6,54,57.
(1)甲群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映甲群游客年龄特征的是 ;
(2)乙群游客的平均年龄是 岁,中位数是 岁,众数是 岁.其中能较好反映乙群游客年龄特征的是 .
众数
定义:出现次数最多的数
平均数、中位数、众数的意义:平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”
1. 习题6.1中第5、6、7题.
2.完成同步练习册中本课时的练习.
