2015年青岛版九年级数学上册期末模拟试题(含答案)
文档属性
| 名称 | 2015年青岛版九年级数学上册期末模拟试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 116.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-27 00:00:00 | ||
图片预览

文档简介
青岛版九年级数学上册期末模拟试题(含答案)
一.选择题(共14小题)
1.(2015 永州)如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD AC D. =
(1题图) (2题图) (3题图)
2.(2015 海南)如图,点P是 ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B. 1对 C. 2对 D. 3对
3.(2015 铜仁市)如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3:4 B. 9:16 C. 9:1 D. 3:1
4.(2015 哈尔滨)如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B. = C. = D. =
(4题图) (5题图) (6题图)
5.(2015 营口)如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
A.(4,2) B. (4,1) C. (5,2) D. (5,1)
6.(2015 山西)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2 B. C. D.
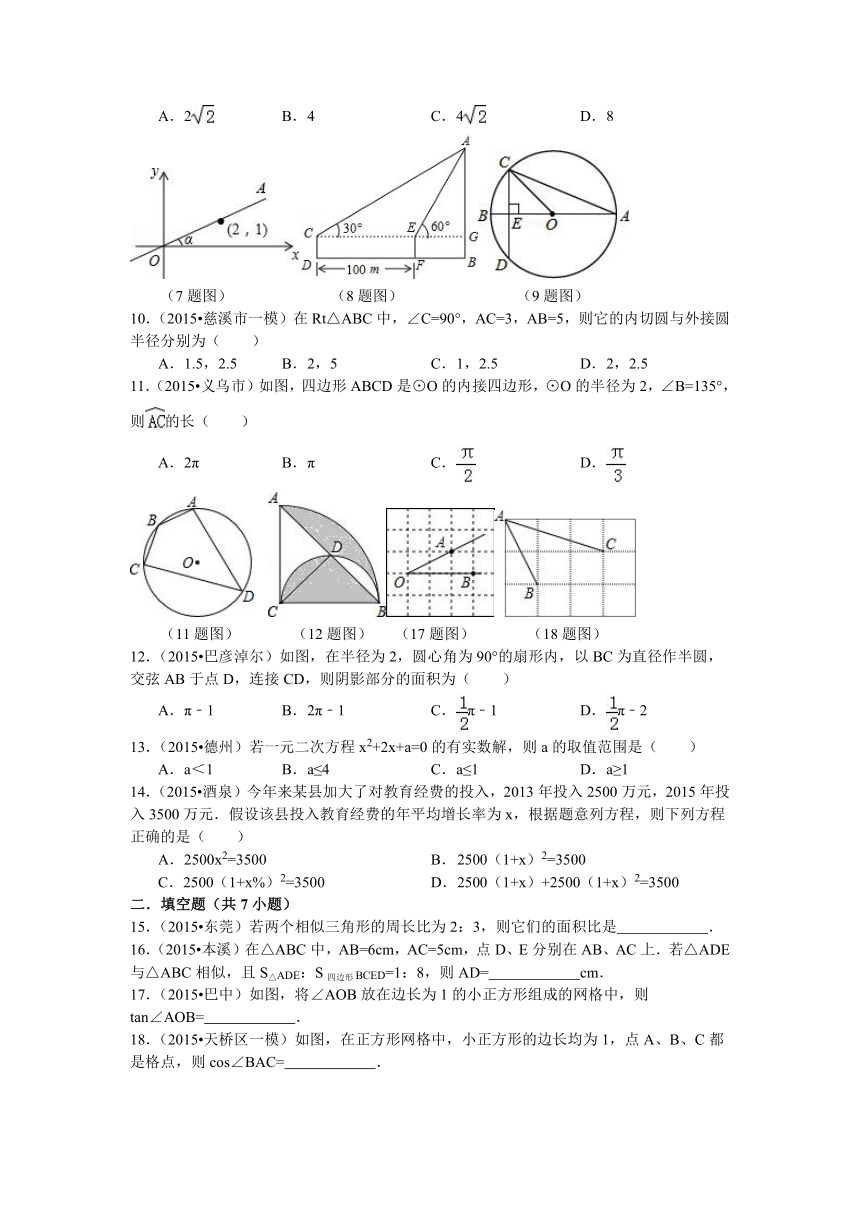
7.(2015 南通)如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
A. B. C. D. 2
8.(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
(2015 安顺)如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
A.2 B. 4 C. 4 D. 8
(7题图) (8题图) (9题图)
10.(2015 慈溪市一模)在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B. 2,5 C. 1,2.5 D. 2,2.5
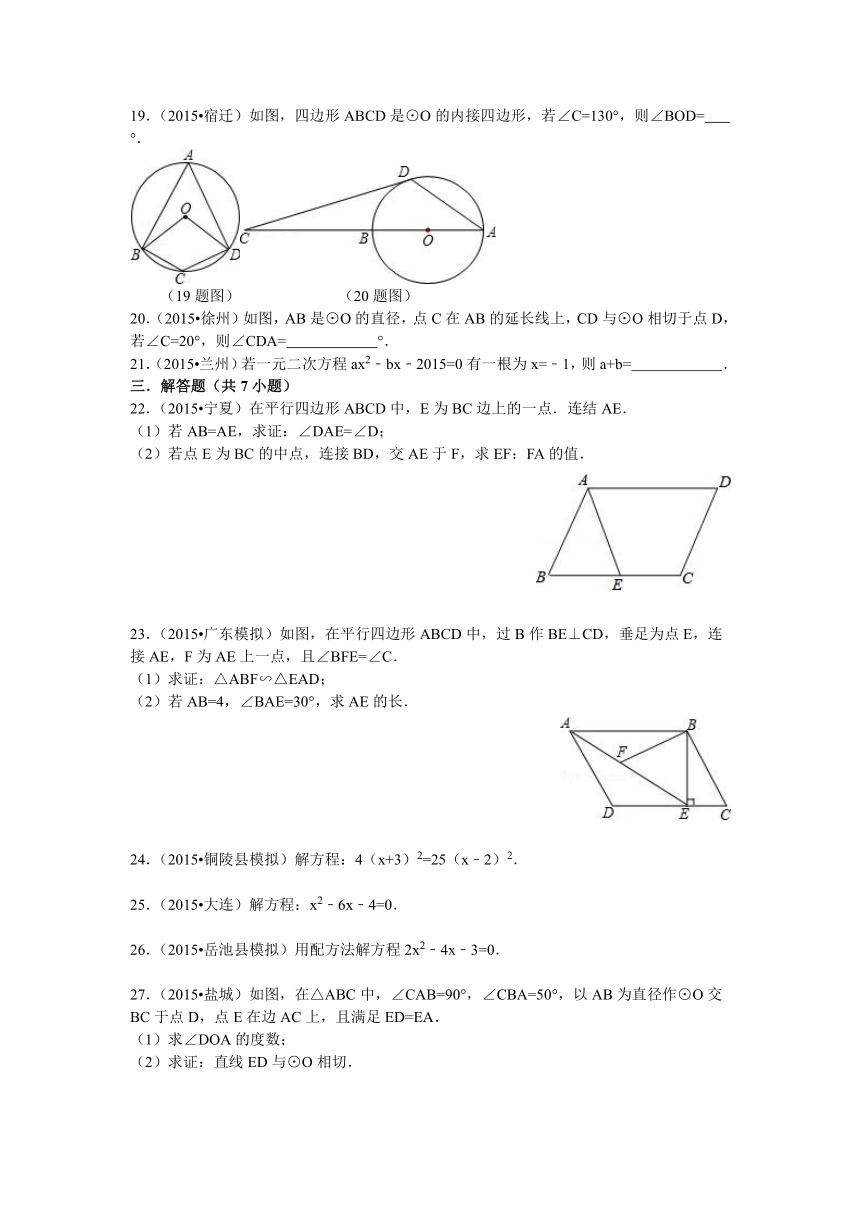
11.(2015 义乌市)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π B. π C. D.
(11题图) (12题图) (17题图) (18题图)
12.(2015 巴彦淖尔)如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
A.π﹣1 B. 2π﹣1 C. π﹣1 D. π﹣2
13.(2015 德州)若一元二次方程x2+2x+a=0的有实数解,则a的取值范围是( )
A.a<1 B. a≤4 C. a≤1 D. a≥1
14.(2015 酒泉)今年来某县加大了对教育经费的投入,2013年投入2500万元,2015年投入3500万元.假设该县投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
A.2500x2=3500 B. 2500(1+x)2=3500
C.2500(1+x%)2=3500 D. 2500(1+x)+2500(1+x)2=3500
二.填空题(共7小题)
15.(2015 东莞)若两个相似三角形的周长比为2:3,则它们的面积比是 .
16.(2015 本溪)在△ABC中,AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD= cm.
17.(2015 巴中)如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
18.(2015 天桥区一模)如图,在正方形网格中,小正方形的边长均为1,点A、B、C都是格点,则cos∠BAC= .
19.(2015 宿迁)如图,四边形ABCD是⊙O的内接四边形,若∠C=130°,则∠BOD= °.
(19题图) (20题图)
20.(2015 徐州)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.
21.(2015 兰州)若一元二次方程ax2﹣bx﹣2015=0有一根为x=﹣1,则a+b= .
三.解答题(共7小题)
22.(2015 宁夏)在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
23.(2015 广东模拟)如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长.
24.(2015 铜陵县模拟)解方程:4(x+3)2=25(x﹣2)2.
25.(2015 大连)解方程:x2﹣6x﹣4=0.
26.(2015 岳池县模拟)用配方法解方程2x2﹣4x﹣3=0.
27.(2015 盐城)如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.
28.(2015 乌鲁木齐)某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定位多少元?
参考答案
一.选择题(共14小题)
1.D.2.D.3.B.4.C.5.C.6.D.7.C.8.C.9.C.10.C.
11.B.12.A.13.C.14.B.
二.填空题(共7小题)
15. 4:9 .16. 2或 cm17. .18. 19. 100 °.20. 125 °21. 2015
三.解答题(共7小题)
22.证明:(1)在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,
∵AE=AB,∴∠ABE=∠AEB,∴∠B=∠EAD,
∵∠B=∠D,∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,∴,
∵E为BC的中点,∴BE=BC=AD,
∴EF:FA=1:2.
23.(1)证明:∵AD∥BC,∴∠C+∠ADE=180°,
∵∠BFE=∠C,∴∠AFB=∠EDA,
∵AB∥DC,∴∠BAE=∠AED,
∴△ABF∽△EAD;
(2)解:∵AB∥CD,BE⊥CD,∴∠ABE=90°,
∵AB=4,∠BAE=30°,∴AE=2BE,
由勾股定理可求得AE=.
24.解:4(x+3)2=25(x﹣2)2,
开方得:2(x+3)=±5(x﹣2),
解得:,.
25.解:移项得x2﹣6x=4,
配方得x2﹣6x+9=4+9,
即(x﹣3)2=13,
开方得x﹣3=±,
∴x1=3+,x2=3﹣.
26.解:∵2x2﹣4x﹣3=0,
∴,
∴,
∴x﹣1=±,
∴.
27.(1)解;∵∠DBA=50°,∴∠DOA=2∠DBA=100°,
证明:连接OE.
在△EAO与△EDO中,,∴△EAO≌△EDO,∴∠EDO=∠EAO,
∵∠BAC=90°,
∴∠EDO=90°,
∴DE与⊙O相切.
28.解:降价x元,则售价为(60﹣x)元,销售量为(300+20x)件,
根据题意得,(60﹣x﹣40)(300+20x)=6080,
解得x1=1,x2=4,
又顾客得实惠,故取x=4,级定价为56元,
答:应将销售单价定位56元.
一.选择题(共14小题)
1.(2015 永州)如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD AC D. =
(1题图) (2题图) (3题图)
2.(2015 海南)如图,点P是 ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B. 1对 C. 2对 D. 3对
3.(2015 铜仁市)如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3:4 B. 9:16 C. 9:1 D. 3:1
4.(2015 哈尔滨)如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B. = C. = D. =
(4题图) (5题图) (6题图)
5.(2015 营口)如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
A.(4,2) B. (4,1) C. (5,2) D. (5,1)
6.(2015 山西)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2 B. C. D.
7.(2015 南通)如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
A. B. C. D. 2
8.(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
(2015 安顺)如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
A.2 B. 4 C. 4 D. 8
(7题图) (8题图) (9题图)
10.(2015 慈溪市一模)在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B. 2,5 C. 1,2.5 D. 2,2.5
11.(2015 义乌市)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π B. π C. D.
(11题图) (12题图) (17题图) (18题图)
12.(2015 巴彦淖尔)如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
A.π﹣1 B. 2π﹣1 C. π﹣1 D. π﹣2
13.(2015 德州)若一元二次方程x2+2x+a=0的有实数解,则a的取值范围是( )
A.a<1 B. a≤4 C. a≤1 D. a≥1
14.(2015 酒泉)今年来某县加大了对教育经费的投入,2013年投入2500万元,2015年投入3500万元.假设该县投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
A.2500x2=3500 B. 2500(1+x)2=3500
C.2500(1+x%)2=3500 D. 2500(1+x)+2500(1+x)2=3500
二.填空题(共7小题)
15.(2015 东莞)若两个相似三角形的周长比为2:3,则它们的面积比是 .
16.(2015 本溪)在△ABC中,AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD= cm.
17.(2015 巴中)如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
18.(2015 天桥区一模)如图,在正方形网格中,小正方形的边长均为1,点A、B、C都是格点,则cos∠BAC= .
19.(2015 宿迁)如图,四边形ABCD是⊙O的内接四边形,若∠C=130°,则∠BOD= °.
(19题图) (20题图)
20.(2015 徐州)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.
21.(2015 兰州)若一元二次方程ax2﹣bx﹣2015=0有一根为x=﹣1,则a+b= .
三.解答题(共7小题)
22.(2015 宁夏)在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
23.(2015 广东模拟)如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长.
24.(2015 铜陵县模拟)解方程:4(x+3)2=25(x﹣2)2.
25.(2015 大连)解方程:x2﹣6x﹣4=0.
26.(2015 岳池县模拟)用配方法解方程2x2﹣4x﹣3=0.
27.(2015 盐城)如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.
28.(2015 乌鲁木齐)某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定位多少元?
参考答案
一.选择题(共14小题)
1.D.2.D.3.B.4.C.5.C.6.D.7.C.8.C.9.C.10.C.
11.B.12.A.13.C.14.B.
二.填空题(共7小题)
15. 4:9 .16. 2或 cm17. .18. 19. 100 °.20. 125 °21. 2015
三.解答题(共7小题)
22.证明:(1)在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,
∵AE=AB,∴∠ABE=∠AEB,∴∠B=∠EAD,
∵∠B=∠D,∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,∴,
∵E为BC的中点,∴BE=BC=AD,
∴EF:FA=1:2.
23.(1)证明:∵AD∥BC,∴∠C+∠ADE=180°,
∵∠BFE=∠C,∴∠AFB=∠EDA,
∵AB∥DC,∴∠BAE=∠AED,
∴△ABF∽△EAD;
(2)解:∵AB∥CD,BE⊥CD,∴∠ABE=90°,
∵AB=4,∠BAE=30°,∴AE=2BE,
由勾股定理可求得AE=.
24.解:4(x+3)2=25(x﹣2)2,
开方得:2(x+3)=±5(x﹣2),
解得:,.
25.解:移项得x2﹣6x=4,
配方得x2﹣6x+9=4+9,
即(x﹣3)2=13,
开方得x﹣3=±,
∴x1=3+,x2=3﹣.
26.解:∵2x2﹣4x﹣3=0,
∴,
∴,
∴x﹣1=±,
∴.
27.(1)解;∵∠DBA=50°,∴∠DOA=2∠DBA=100°,
证明:连接OE.
在△EAO与△EDO中,,∴△EAO≌△EDO,∴∠EDO=∠EAO,
∵∠BAC=90°,
∴∠EDO=90°,
∴DE与⊙O相切.
28.解:降价x元,则售价为(60﹣x)元,销售量为(300+20x)件,
根据题意得,(60﹣x﹣40)(300+20x)=6080,
解得x1=1,x2=4,
又顾客得实惠,故取x=4,级定价为56元,
答:应将销售单价定位56元.
同课章节目录
