余角补角教案
图片预览
文档简介
4.3.3 余角和补角
教学目标:
知识与技能:掌握余角和补角的概念及其几何语言的表示方法,会计算一个角的余角和补角,能从图形中找出互余或互补的角。
过程与方法:引导学生得出余、补角的性质,培养他们简单说理的能力;引导学生对余补角性质的探究,培养他们的作图能力、几何语言表述能力以及图形语言和几何语言的互化能力。
情感态度价值观:让学生体会事物总是运动变化的,在运动变化中又总是相互联系的,同时培养学生的探索精神。
教学重点:余补角的概念以及余补角的性质
教学难点:余补角性质的应用探究
教学过程:
一 :引入概念。
1. 学有理数时,如果把两个数放在一起时我们研究什么?
(两个数的大小关系,两个数之间的运算,特别地,有一些特殊的运算关系:如相反数、倒数等)
那么在学角时,单独一个角我们研究什么呢 (角度大小,摆放位置) 两个角在一起时研究什么?(两个角的数量关系与位置关系)
问题1:
从数量关系来看,图一中的两个角与图二中的两个角有何共同特征?
图1 图2
答:∠ A+∠B=90°.
定义:当两个角的和为90°(直角)时,就说这两个角互余。即其中一个角是另一个角的余角。
(在代数中学过类似的概念吗:相反数、倒数)
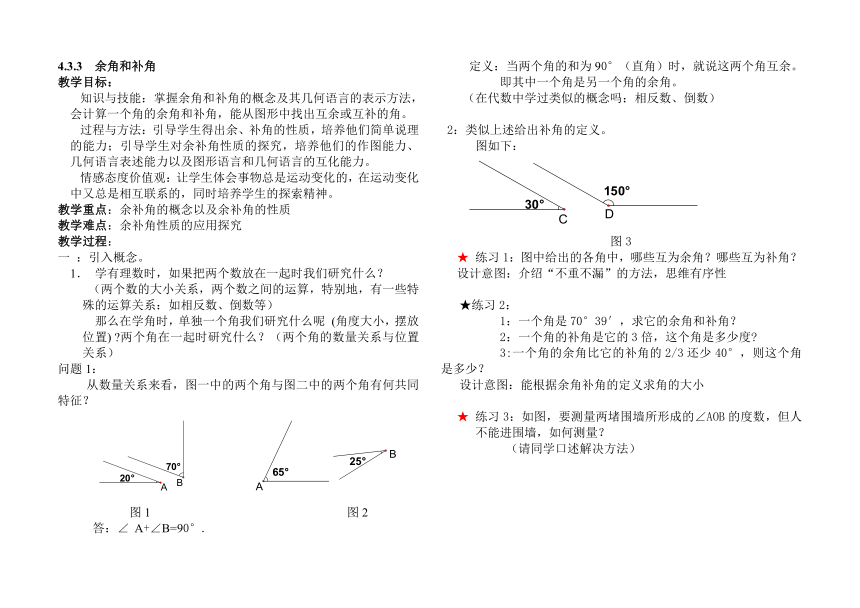
2:类似上述给出补角的定义。
图如下:
图3
★ 练习1:图中给出的各角中,哪些互为余角?哪些互为补角?
设计意图:介绍“不重不漏”的方法,思维有序性
★练习2:
1:一个角是70°39′,求它的余角和补角?
2:一个角的补角是它的3倍,这个角是多少度
3:一个角的余角比它的补角的2/3还少40°,则这个角是多少?
设计意图:能根据余角补角的定义求角的大小
★ 练习3:如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进围墙,如何测量?
(请同学口述解决方法)
图4
补充“邻补角”的概念
注:“邻补角”既有数量关系,又有数量关系。(有一条公共边)。
“邻余角 ”的概念?
设计意图:补充“邻补角”概念,训练几何语言表述。
二:余角、补角性质及其应用
问题2:
(1) 如果∠ 1 = ∠ 2,
∠ 3 = ∠ 2,
则∠ 1 ∠ 3.
(2)如果∠1 = ∠3,
∠2 = ∠4,
且∠3 = ∠4,
则∠1 ∠2。
(3)如图,如果∠1=∠3,∠1与∠2互补,∠3与∠4互补,,那么∠2与∠4相等吗?为什么?
解: ∠2与∠4相等
∵∠1与∠2互补
∴∠2 = 180°-∠1
∵∠3与∠4互补
∴∠4 = 180°-∠3
∵ ∠ 1=∠3
∴ 180°-∠1=180°-∠3
∴∠2=∠4
补角性质:等角的补角相等。
师:今天还学了余角的概念,类似的结论该怎么说?是否正确呢?
余角性质:“等角的余角相等”。
探究一:
1.如图5,线段AB与线段CD重合,O点是线段上一点,现在将线段CD绕点O转动到图6的位置,问图6中的∠1,∠2,∠3之间有何数量关系?(动态演示)
图5 图6
(静态的看图6,应该有什么结论呢?)
设计意图:为后续学习的对顶角知识做铺垫
2.如图7,直角∠AOB与直角∠COD重合,现在将∠COD绕点O转动到图8的位置,问图8中的∠1,∠2,∠3之间有何数量关系?(动态演示)
图7 图8
设计意图:为后续学习旋转知识做铺垫
作图题:先画一个锐角∠AOB,借助作图工具再画一个角与∠AOB相等,你能想出几种作法呢?
设计意图:训练学生的作图能力
探究二:
1. 如图9,O是直线l上一点,∠AOB是直角,图中∠1与∠2的有什么关系?
(动态演示∠AOB 绕点O旋转)
图9 图10
设计意图:为后续学习相似形知识做铺垫
2,根据指令语言画出图形
先画直角∠AOB;
再画射线OC。
图中的∠AOC与∠BOC有何数量关系呢?
设计意图:训练学生的作图能力以及思维的严谨性
3,如图11,∠AOE,∠BOE,∠COD都是直角,找出图中相等的角,互余角,互补角。
图11
设计意图:培养学生的识图能力
课堂小结:1、两个角的特殊数量关系:互余、互补;
2、余角的性质,补角的性质;
3、与性质有关的一些基本图形
备用例题:
如图,直线CD、EF相交于点O,OA⊥OB,且OC平分
∠AOF,BOE=2∠AOE,求角∠BOD的度数?
教学目标:
知识与技能:掌握余角和补角的概念及其几何语言的表示方法,会计算一个角的余角和补角,能从图形中找出互余或互补的角。
过程与方法:引导学生得出余、补角的性质,培养他们简单说理的能力;引导学生对余补角性质的探究,培养他们的作图能力、几何语言表述能力以及图形语言和几何语言的互化能力。
情感态度价值观:让学生体会事物总是运动变化的,在运动变化中又总是相互联系的,同时培养学生的探索精神。
教学重点:余补角的概念以及余补角的性质
教学难点:余补角性质的应用探究
教学过程:
一 :引入概念。
1. 学有理数时,如果把两个数放在一起时我们研究什么?
(两个数的大小关系,两个数之间的运算,特别地,有一些特殊的运算关系:如相反数、倒数等)
那么在学角时,单独一个角我们研究什么呢 (角度大小,摆放位置) 两个角在一起时研究什么?(两个角的数量关系与位置关系)
问题1:
从数量关系来看,图一中的两个角与图二中的两个角有何共同特征?
图1 图2
答:∠ A+∠B=90°.
定义:当两个角的和为90°(直角)时,就说这两个角互余。即其中一个角是另一个角的余角。
(在代数中学过类似的概念吗:相反数、倒数)
2:类似上述给出补角的定义。
图如下:
图3
★ 练习1:图中给出的各角中,哪些互为余角?哪些互为补角?
设计意图:介绍“不重不漏”的方法,思维有序性
★练习2:
1:一个角是70°39′,求它的余角和补角?
2:一个角的补角是它的3倍,这个角是多少度
3:一个角的余角比它的补角的2/3还少40°,则这个角是多少?
设计意图:能根据余角补角的定义求角的大小
★ 练习3:如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进围墙,如何测量?
(请同学口述解决方法)
图4
补充“邻补角”的概念
注:“邻补角”既有数量关系,又有数量关系。(有一条公共边)。
“邻余角 ”的概念?
设计意图:补充“邻补角”概念,训练几何语言表述。
二:余角、补角性质及其应用
问题2:
(1) 如果∠ 1 = ∠ 2,
∠ 3 = ∠ 2,
则∠ 1 ∠ 3.
(2)如果∠1 = ∠3,
∠2 = ∠4,
且∠3 = ∠4,
则∠1 ∠2。
(3)如图,如果∠1=∠3,∠1与∠2互补,∠3与∠4互补,,那么∠2与∠4相等吗?为什么?
解: ∠2与∠4相等
∵∠1与∠2互补
∴∠2 = 180°-∠1
∵∠3与∠4互补
∴∠4 = 180°-∠3
∵ ∠ 1=∠3
∴ 180°-∠1=180°-∠3
∴∠2=∠4
补角性质:等角的补角相等。
师:今天还学了余角的概念,类似的结论该怎么说?是否正确呢?
余角性质:“等角的余角相等”。
探究一:
1.如图5,线段AB与线段CD重合,O点是线段上一点,现在将线段CD绕点O转动到图6的位置,问图6中的∠1,∠2,∠3之间有何数量关系?(动态演示)
图5 图6
(静态的看图6,应该有什么结论呢?)
设计意图:为后续学习的对顶角知识做铺垫
2.如图7,直角∠AOB与直角∠COD重合,现在将∠COD绕点O转动到图8的位置,问图8中的∠1,∠2,∠3之间有何数量关系?(动态演示)
图7 图8
设计意图:为后续学习旋转知识做铺垫
作图题:先画一个锐角∠AOB,借助作图工具再画一个角与∠AOB相等,你能想出几种作法呢?
设计意图:训练学生的作图能力
探究二:
1. 如图9,O是直线l上一点,∠AOB是直角,图中∠1与∠2的有什么关系?
(动态演示∠AOB 绕点O旋转)
图9 图10
设计意图:为后续学习相似形知识做铺垫
2,根据指令语言画出图形
先画直角∠AOB;
再画射线OC。
图中的∠AOC与∠BOC有何数量关系呢?
设计意图:训练学生的作图能力以及思维的严谨性
3,如图11,∠AOE,∠BOE,∠COD都是直角,找出图中相等的角,互余角,互补角。
图11
设计意图:培养学生的识图能力
课堂小结:1、两个角的特殊数量关系:互余、互补;
2、余角的性质,补角的性质;
3、与性质有关的一些基本图形
备用例题:
如图,直线CD、EF相交于点O,OA⊥OB,且OC平分
∠AOF,BOE=2∠AOE,求角∠BOD的度数?
