寒假预习课:第二十六章反比例函数2023-2024学年数学九年级下册人教版(含答案)
文档属性
| 名称 | 寒假预习课:第二十六章反比例函数2023-2024学年数学九年级下册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-07 09:42:19 | ||
图片预览

文档简介
寒假预习课:第二十六章反比例函数2023-2024学年数学九年级下册人教版
一、选择题
1.已知点在反比例的数的图象上.其中.下列结论正确的是( )
A. B. C. D.
2.在平面直角坐标系中,对于横、纵坐标相等的点称为“完美点”.下列函数的图象中不存在“完美点”的是( )
A. B. C. D.
3.方程的根可视为函数的图象与函数的图象交点的横坐标,则方程的实根所在的范围是( )
A. B. C. D.
4.如图,一次函数的图象与轴交于点,与y轴交于点,与反比例函数的图象交于点,.若,,则点的坐标为( )
A. B. C. D.
5.如图,在平面直角坐标系中,菱形在第一象限内,边与轴平行,,两点纵坐标分别为6,4,反比例函数的图象经过,两点.若菱形的面积为,则值为( ).
A.8 B.12 C.10 D.9
6.若,则正比例函数与反比例函数在同一平面直角坐标系中的大致图像可能是( )
A. B.
C. D.
7.如图,函数与函数的图象相交于A、B两点,轴,轴,则的面积等于( )
A.18 B.12 C.6 D.3
8.在平面直角坐标系xOy中,矩形OBCD的顶点B在x轴正半轴上,顶点D在y轴正半轴上如图,若反比例函数y=(x>0)的图象与CD交于点M,与BC交于点N,CM=2DM,连接OM,ON,MN,则( )
A. B. C. D.1
二、填空题
9.已知函数y与自变量x的部分对应值如表:
x … -5 -2 2 5 …
y … -2 m 5 n …
下列命题:①若y是x的反比例函数,则;②若y是x的一次函数,则;③若y是x的二次函数,且图象开口向下,则.其中正确的是 .(填写正确的序号)
10.已知反比例函数与直线相交于点,点的横坐标为,则此反比例函数的解析式为 .
11.在函数①;②;③;④中随的增大而减小的有 个.
12.如图,在平面直角坐标系中,菱形的顶点A在x轴上,顶点C在反比例函数的图象上,且若将该菱形向下平移2个单位后,顶点B恰好落在此反比例函数的图象上,则此反比例函数的表达式为 .
13.把一块含60°角的三角板按图方式摆放在平面直角坐标系中,其中60°角的顶点B在x轴上,斜边与x轴的夹角,若,当点A,C同时落在一个反比例函数图象上时,B点的坐标为 .
14.若关于t的不等式组,恰有三个整数解,则关于x的一次函数的图象与反比例函数的图象的公共点的个数为 .
15.如图,反比例函数经过的直角边上一点C,且,若,则k= .
16.如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为,则不等式的解集是 .
三、解答题
17.已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
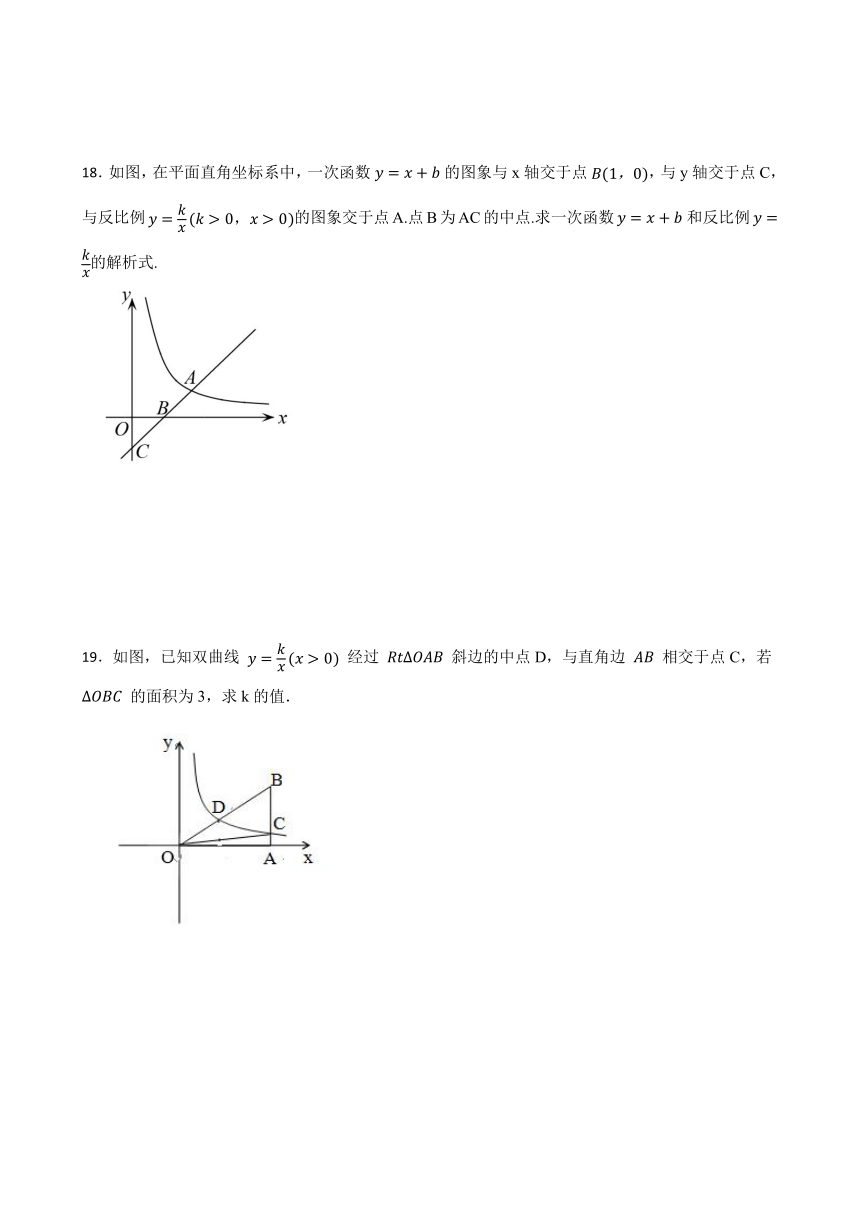
18.如图,在平面直角坐标系中,一次函数的图象与x轴交于点,与y轴交于点C,与反比例的图象交于点A.点B为AC的中点.求一次函数和反比例的解析式.
19.如图,已知双曲线 经过 斜边的中点D,与直角边 相交于点C,若 的面积为3,求k的值.
20.如图,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.求△ABC的面积.
21.某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
22.设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=x2﹣2x﹣k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】①②
10.【答案】
11.【答案】2
12.【答案】
13.【答案】(5,0)
14.【答案】1或0
15.【答案】3
16.【答案】-1<x<0或x>2
17.【答案】解:∵y1与x成正比例,∴y1=kx,∵y2与x+2成反比例,∴y2= ,∵y=y1+y2,∴y=kx+ ,∵当x=﹣1时,y=3;当x=3时,y=7,∴ ,解得: ,∴y=2x+ ,当x=﹣3时,y=2×(﹣3)﹣5=﹣11
18.【答案】解:把点代入得:,
解得:,
∴一次函数的解析式,
当时,,
∴,
如图,作轴,垂足为D,
在和中,
∴,
∴,,
∴,
∵点在反比例函数
∴,
∴反比例的解析式.
19.【答案】解:过点D做 轴,垂足为E,
∵ 中, ,
∴
∵D为 斜边 的中点,
∴ 为 的中位线
∴ 且
∵双曲线的解析式是
∴ ,
解得
20.【答案】解:∵,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.
∴A(3,3),B(1,1),
∴OA=AC=3 ,OB= ,
∴AB=3 ﹣ =2 ,
∴S= AB AC= ×2 ×3 =6
21.【答案】(1)解:由(1)设甲种品牌的进价为x元,则乙种品牌空调的进价为(1+20%)x元,
由题意,得 ,
解得x=1500,
经检验,x=1500是原分式方程的解.
乙种品牌空调的进价为(1+20%)×1500=1800(元).
答案:甲种品牌的进价为1500元,乙种品牌空调的进价为1800元.
(2)解:设购进甲种品牌空调a台,则购进乙种品牌空调(10-a)台,
由题意,得1500a+1800(10-a)≤16000,
解得 ≤a,
设利润为w,则w=(2500-1500)a+(3500-1800)(10-a)=-700a+17000,
因为-700<0,则w随a的增大而减少,当a=7时,w最大,最大为12100元.
答:当购进甲种品牌空调7台,乙种品牌空调3台时,售完后利润最大,最大为12100元.
22.【答案】解:(1)反比例函数y=是闭区间[1,2015]上的“闭函数”.理由如下:
反比例函数y=在第一象限,y随x的增大而减小,
当x=1时,y=2015;
当x=2015时,y=1,
即图象过点(1,2015)和(2015,1)
∴当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,
∴反比例函数y=是闭区间[1,2015]上的“闭函数”;
(2)由于二次函数y=x2﹣2x﹣k的图象开口向上,
对称轴为x=1,
∴二次函数y=x2﹣2x﹣k在闭区间[1,2]内,y随x的增大而增大.
当x=1时,y=1,
∴k=﹣2;
当x=2时,y=2,
∴k=﹣2;
即图象过点(1,1)和(2,2),
∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义,
∴k=﹣2.
(3)因为一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,
根据一次函数的图象与性质,有:
(Ⅰ)当k>0时,即图象过点(m,m)和(n,n),
,
解得,
∴y=x;
(Ⅱ)当k<0时,即图象过点(m,n)和(n,m),
可得:,
解得,
∴y=﹣x+m+n,
∴一次函数的解析式为y=x或y=﹣x+m+n.
一、选择题
1.已知点在反比例的数的图象上.其中.下列结论正确的是( )
A. B. C. D.
2.在平面直角坐标系中,对于横、纵坐标相等的点称为“完美点”.下列函数的图象中不存在“完美点”的是( )
A. B. C. D.
3.方程的根可视为函数的图象与函数的图象交点的横坐标,则方程的实根所在的范围是( )
A. B. C. D.
4.如图,一次函数的图象与轴交于点,与y轴交于点,与反比例函数的图象交于点,.若,,则点的坐标为( )
A. B. C. D.
5.如图,在平面直角坐标系中,菱形在第一象限内,边与轴平行,,两点纵坐标分别为6,4,反比例函数的图象经过,两点.若菱形的面积为,则值为( ).
A.8 B.12 C.10 D.9
6.若,则正比例函数与反比例函数在同一平面直角坐标系中的大致图像可能是( )
A. B.
C. D.
7.如图,函数与函数的图象相交于A、B两点,轴,轴,则的面积等于( )
A.18 B.12 C.6 D.3
8.在平面直角坐标系xOy中,矩形OBCD的顶点B在x轴正半轴上,顶点D在y轴正半轴上如图,若反比例函数y=(x>0)的图象与CD交于点M,与BC交于点N,CM=2DM,连接OM,ON,MN,则( )
A. B. C. D.1
二、填空题
9.已知函数y与自变量x的部分对应值如表:
x … -5 -2 2 5 …
y … -2 m 5 n …
下列命题:①若y是x的反比例函数,则;②若y是x的一次函数,则;③若y是x的二次函数,且图象开口向下,则.其中正确的是 .(填写正确的序号)
10.已知反比例函数与直线相交于点,点的横坐标为,则此反比例函数的解析式为 .
11.在函数①;②;③;④中随的增大而减小的有 个.
12.如图,在平面直角坐标系中,菱形的顶点A在x轴上,顶点C在反比例函数的图象上,且若将该菱形向下平移2个单位后,顶点B恰好落在此反比例函数的图象上,则此反比例函数的表达式为 .
13.把一块含60°角的三角板按图方式摆放在平面直角坐标系中,其中60°角的顶点B在x轴上,斜边与x轴的夹角,若,当点A,C同时落在一个反比例函数图象上时,B点的坐标为 .
14.若关于t的不等式组,恰有三个整数解,则关于x的一次函数的图象与反比例函数的图象的公共点的个数为 .
15.如图,反比例函数经过的直角边上一点C,且,若,则k= .
16.如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为,则不等式的解集是 .
三、解答题
17.已知y=y1+y2,y1与x成正比例,y2与x+2成反比例,且当x=﹣1时,y=3;当x=3时,y=7.求x=﹣3时,y的值.
18.如图,在平面直角坐标系中,一次函数的图象与x轴交于点,与y轴交于点C,与反比例的图象交于点A.点B为AC的中点.求一次函数和反比例的解析式.
19.如图,已知双曲线 经过 斜边的中点D,与直角边 相交于点C,若 的面积为3,求k的值.
20.如图,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.求△ABC的面积.
21.某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
22.设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=x2﹣2x﹣k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】①②
10.【答案】
11.【答案】2
12.【答案】
13.【答案】(5,0)
14.【答案】1或0
15.【答案】3
16.【答案】-1<x<0或x>2
17.【答案】解:∵y1与x成正比例,∴y1=kx,∵y2与x+2成反比例,∴y2= ,∵y=y1+y2,∴y=kx+ ,∵当x=﹣1时,y=3;当x=3时,y=7,∴ ,解得: ,∴y=2x+ ,当x=﹣3时,y=2×(﹣3)﹣5=﹣11
18.【答案】解:把点代入得:,
解得:,
∴一次函数的解析式,
当时,,
∴,
如图,作轴,垂足为D,
在和中,
∴,
∴,,
∴,
∵点在反比例函数
∴,
∴反比例的解析式.
19.【答案】解:过点D做 轴,垂足为E,
∵ 中, ,
∴
∵D为 斜边 的中点,
∴ 为 的中位线
∴ 且
∵双曲线的解析式是
∴ ,
解得
20.【答案】解:∵,△OAC是等腰直角三角形,直角顶点A在函数y= (x>0)图象上,边OA交函数y= (x>0)的图象于点B.
∴A(3,3),B(1,1),
∴OA=AC=3 ,OB= ,
∴AB=3 ﹣ =2 ,
∴S= AB AC= ×2 ×3 =6
21.【答案】(1)解:由(1)设甲种品牌的进价为x元,则乙种品牌空调的进价为(1+20%)x元,
由题意,得 ,
解得x=1500,
经检验,x=1500是原分式方程的解.
乙种品牌空调的进价为(1+20%)×1500=1800(元).
答案:甲种品牌的进价为1500元,乙种品牌空调的进价为1800元.
(2)解:设购进甲种品牌空调a台,则购进乙种品牌空调(10-a)台,
由题意,得1500a+1800(10-a)≤16000,
解得 ≤a,
设利润为w,则w=(2500-1500)a+(3500-1800)(10-a)=-700a+17000,
因为-700<0,则w随a的增大而减少,当a=7时,w最大,最大为12100元.
答:当购进甲种品牌空调7台,乙种品牌空调3台时,售完后利润最大,最大为12100元.
22.【答案】解:(1)反比例函数y=是闭区间[1,2015]上的“闭函数”.理由如下:
反比例函数y=在第一象限,y随x的增大而减小,
当x=1时,y=2015;
当x=2015时,y=1,
即图象过点(1,2015)和(2015,1)
∴当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,
∴反比例函数y=是闭区间[1,2015]上的“闭函数”;
(2)由于二次函数y=x2﹣2x﹣k的图象开口向上,
对称轴为x=1,
∴二次函数y=x2﹣2x﹣k在闭区间[1,2]内,y随x的增大而增大.
当x=1时,y=1,
∴k=﹣2;
当x=2时,y=2,
∴k=﹣2;
即图象过点(1,1)和(2,2),
∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义,
∴k=﹣2.
(3)因为一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,
根据一次函数的图象与性质,有:
(Ⅰ)当k>0时,即图象过点(m,m)和(n,n),
,
解得,
∴y=x;
(Ⅱ)当k<0时,即图象过点(m,n)和(n,m),
可得:,
解得,
∴y=﹣x+m+n,
∴一次函数的解析式为y=x或y=﹣x+m+n.
