寒假预习课:第五章 二次函数2023-2024学年数学九年级下册苏科版(含答案)
文档属性
| 名称 | 寒假预习课:第五章 二次函数2023-2024学年数学九年级下册苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-08 10:29:04 | ||
图片预览



文档简介
寒假预习课:第五章二次函数2023-2024学年数学九年级下册苏科版
一、选择题
1.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y﹣2=0 C.y2﹣ax=﹣2 D.x2﹣y2+1=0
2.把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2+3 B.y=﹣(x+1)2+3
C.y=﹣(x+1)2﹣3 D.y=﹣(x﹣1)2﹣3
3.已知二次函数,关于该函数在的取值范围内,下列说法项正确的是( )
A.若,函数有最大值5 B.若,函数有最小值5
C.若,函数有最小值1 D.若,函数无最大值
4.已知二次函数,与的部分对应值为:
-2 -1 0 1 2
-1 2 3 2 ?
关于此函数的图象和性质,下列说法正确的是( )
A.当时,函数图象从左到右上升
B.抛物线开口向上
C.方程的一个根在-2与-1之间
D.当时,
5.已知二次函数y=x2-2x+2在m≤x≤m+1时有最小值m,则整数m的值是( )
A.1 B.2 C.1或2 D.±1或2
6.已知二次函数的图象如下所示,下列5个结论:①;②;③;④;⑤(的实数),其中正确的结论有几个?
A.①②③ B.②③④ C.②③⑤ D.③④⑤
7.已知二次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线与新图像有3个交点时,m的值是( )
A. B.-2 C.-2或3 D.-6或-2
8.已知二次函数(a为实数,且),对于满足的任意一个x的值,都有,则的最大值为( )
A. B. C. D.
二、填空题
9.某企业今年第一月新产品的研发资金为100万元,以后每月新产品的研发资金与上月相比增长的都是x,则该厂今年第三月新产品的研发资金y(元)关于x的函数关系式为y= .
10.将二次函数的图像向上平移a个单位长度,当抛物线经过点时,a的值为 ;当抛物线与两坐标轴有且只有2个公共点时,a的值为 .
11.已知二次函数当时,的取值范围是,该二次函数的对称轴为,则的取值范围是 .
12.如图,一座拱桥的轮廓是抛物线型.拱高6m,跨度20m,相邻两支柱间的距离均为5m,则支柱的长度为 m.
13.如图,抛物线y=ax2+c与直线y=kx+b交于A(-1,m),B(2,n)两点,则不等式ax2-kx+c<b的解集是 .
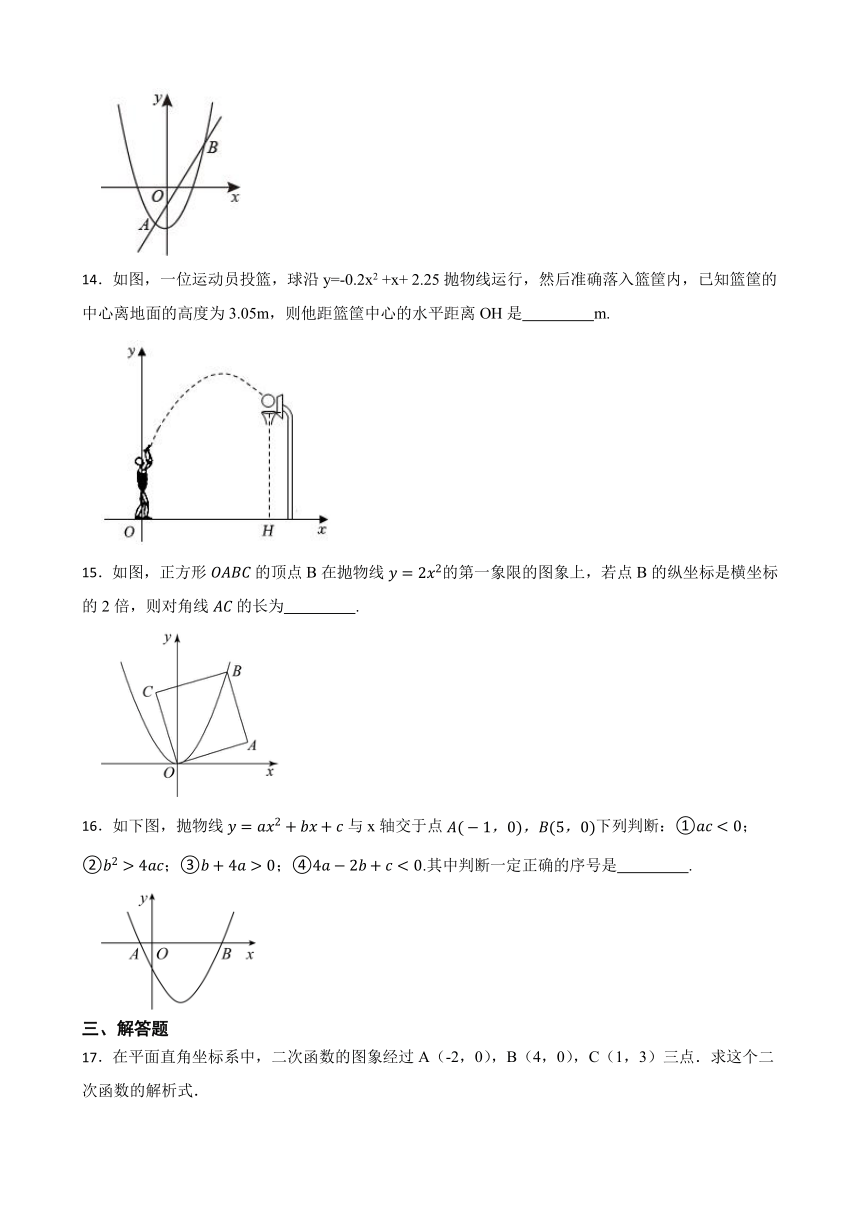
14.如图,一位运动员投篮,球沿y=-0.2x2 +x+ 2.25抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为3.05m,则他距篮筐中心的水平距离OH是 m.
15.如图,正方形的顶点B在抛物线的第一象限的图象上,若点B的纵坐标是横坐标的2倍,则对角线的长为 .
16.如下图,抛物线与x轴交于点下列判断:①;②;③;④.其中判断一定正确的序号是 .
三、解答题
17.在平面直角坐标系中,二次函数的图象经过A(-2,0),B(4,0),C(1,3)三点.求这个二次函数的解析式.
18.给定关于 的二次函数 ,
学生甲:当 时,抛物线与 轴只有一个交点,因此当抛物线与 轴只有一个交点时, 的值为3;
学生乙:如果抛物线在 轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
19.某家电生产厂家去年销往农村的某品牌洗碗机每台的售价y(元)与月份x之间满足函数关系,去年的月销售量P(万台)与月份x之间成一次函数关系y=-50x+2600,其中两个月的销售情况如下表:
月份x 1月 5月
销量P 3.9万台 4.3万台
求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?
20.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.
21.如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0)。点P是直线BC上方的抛物线上一动点
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POPC.若四边形POP'C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
22.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】100(1+x)2
10.【答案】4;3或7
11.【答案】
12.【答案】
13.【答案】-1<x<2
14.【答案】4
15.【答案】
16.【答案】①②
17.【答案】解:∵二次函数的图象经过A(-2,0),B(4,0),
∴设二次函数的解析式为 ,
∵图象过点C(1,3),
∴ ,
解得: ,
∴二次函数的解析式为 ,
故二次函数的解析式为: .
18.【答案】解:甲的观点是错误的.理由如下:当抛物线 与 轴只有一个交点时 即: 解得 或 即 或 时抛物线 与 轴只有一个交点乙的观点是正确的理由如下:当抛物线在 轴上方时,由上可得 即: ∴而对于开口向上的抛物线最低点为其顶点顶点的横坐标为 ,且抛物线在 轴上方,即抛物线的最低点在第二象限
19.【答案】解:设p与x的函数关系式为p=kx+b(k≠0),
根据题意,得
解得:
∴p=0.1x+3.8,
设月销售金额为w万元,
则w=py=(0.1x+3.8)(-50x+2600),
=-5x2+70x+9880
=-5(x-7)2+10125,
当x=7时,w取得最大值为10125.
答:该品牌洗碗机在去年7月销往农村的销售金额最大,最大是10125万元.
20.【答案】解:∵与墙平行的边的长为x(m),
则垂直于墙的边长为: =(25﹣0.5x)m,
根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
21.【答案】(1)解:将点B和点C的坐标代入y=a2+2x+c,得
解得
∴该二次函数的表达式为y=-x2+2x+3
(2)解:若四边形POPC是菱形,则点P在线段CO的垂直平分线上;如图,连接PP,则PELCO,垂足为E,
∵C(0,3),
∴E(0, ),
∴.点P的纵坐标等于 。
∴-x2+2x+3=
解得x1= ,x1= (不合题意,舍去),
∴点P的坐标为( , )
(3)解:过点P作y轴的平行线与BC交于点2,与OB交于点F,
设P(m,-m2+2m+3),设直线BC的表达式为y=kx+3,
则3k+3=0,解得k=-1.
∴直线BC的表达式为y=-x+3.
∴Q点的坐标为(m,-m+3),
∴QP=-m2+3m.
当-x2+2x+3=0,
解得x1=-1,x2=3,
∴AO=1,AB=4,
∴S四边形ABPC=S△ABC+S△CPQ+S△BPQ
=- AB·OC+ QP·OF+ QP·FB
= ×4×3+ (-m2+3m)×3.
当m= 时,四边形ABPC的面积最大。
此时P点的坐标为( , ),四边形ABPC的面积的最大值为
22.【答案】解:∵PB=6﹣t,BE+EQ=6+t,
∴S= PB BQ= PB (BE+EQ)
= (6﹣t)(6+t)
=﹣ t2+18,
∴S=﹣ t2+18(0≤t<6).
一、选择题
1.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y﹣2=0 C.y2﹣ax=﹣2 D.x2﹣y2+1=0
2.把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2+3 B.y=﹣(x+1)2+3
C.y=﹣(x+1)2﹣3 D.y=﹣(x﹣1)2﹣3
3.已知二次函数,关于该函数在的取值范围内,下列说法项正确的是( )
A.若,函数有最大值5 B.若,函数有最小值5
C.若,函数有最小值1 D.若,函数无最大值
4.已知二次函数,与的部分对应值为:
-2 -1 0 1 2
-1 2 3 2 ?
关于此函数的图象和性质,下列说法正确的是( )
A.当时,函数图象从左到右上升
B.抛物线开口向上
C.方程的一个根在-2与-1之间
D.当时,
5.已知二次函数y=x2-2x+2在m≤x≤m+1时有最小值m,则整数m的值是( )
A.1 B.2 C.1或2 D.±1或2
6.已知二次函数的图象如下所示,下列5个结论:①;②;③;④;⑤(的实数),其中正确的结论有几个?
A.①②③ B.②③④ C.②③⑤ D.③④⑤
7.已知二次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线与新图像有3个交点时,m的值是( )
A. B.-2 C.-2或3 D.-6或-2
8.已知二次函数(a为实数,且),对于满足的任意一个x的值,都有,则的最大值为( )
A. B. C. D.
二、填空题
9.某企业今年第一月新产品的研发资金为100万元,以后每月新产品的研发资金与上月相比增长的都是x,则该厂今年第三月新产品的研发资金y(元)关于x的函数关系式为y= .
10.将二次函数的图像向上平移a个单位长度,当抛物线经过点时,a的值为 ;当抛物线与两坐标轴有且只有2个公共点时,a的值为 .
11.已知二次函数当时,的取值范围是,该二次函数的对称轴为,则的取值范围是 .
12.如图,一座拱桥的轮廓是抛物线型.拱高6m,跨度20m,相邻两支柱间的距离均为5m,则支柱的长度为 m.
13.如图,抛物线y=ax2+c与直线y=kx+b交于A(-1,m),B(2,n)两点,则不等式ax2-kx+c<b的解集是 .
14.如图,一位运动员投篮,球沿y=-0.2x2 +x+ 2.25抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为3.05m,则他距篮筐中心的水平距离OH是 m.
15.如图,正方形的顶点B在抛物线的第一象限的图象上,若点B的纵坐标是横坐标的2倍,则对角线的长为 .
16.如下图,抛物线与x轴交于点下列判断:①;②;③;④.其中判断一定正确的序号是 .
三、解答题
17.在平面直角坐标系中,二次函数的图象经过A(-2,0),B(4,0),C(1,3)三点.求这个二次函数的解析式.
18.给定关于 的二次函数 ,
学生甲:当 时,抛物线与 轴只有一个交点,因此当抛物线与 轴只有一个交点时, 的值为3;
学生乙:如果抛物线在 轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
19.某家电生产厂家去年销往农村的某品牌洗碗机每台的售价y(元)与月份x之间满足函数关系,去年的月销售量P(万台)与月份x之间成一次函数关系y=-50x+2600,其中两个月的销售情况如下表:
月份x 1月 5月
销量P 3.9万台 4.3万台
求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?
20.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.
21.如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0)。点P是直线BC上方的抛物线上一动点
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POPC.若四边形POP'C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
22.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】100(1+x)2
10.【答案】4;3或7
11.【答案】
12.【答案】
13.【答案】-1<x<2
14.【答案】4
15.【答案】
16.【答案】①②
17.【答案】解:∵二次函数的图象经过A(-2,0),B(4,0),
∴设二次函数的解析式为 ,
∵图象过点C(1,3),
∴ ,
解得: ,
∴二次函数的解析式为 ,
故二次函数的解析式为: .
18.【答案】解:甲的观点是错误的.理由如下:当抛物线 与 轴只有一个交点时 即: 解得 或 即 或 时抛物线 与 轴只有一个交点乙的观点是正确的理由如下:当抛物线在 轴上方时,由上可得 即: ∴而对于开口向上的抛物线最低点为其顶点顶点的横坐标为 ,且抛物线在 轴上方,即抛物线的最低点在第二象限
19.【答案】解:设p与x的函数关系式为p=kx+b(k≠0),
根据题意,得
解得:
∴p=0.1x+3.8,
设月销售金额为w万元,
则w=py=(0.1x+3.8)(-50x+2600),
=-5x2+70x+9880
=-5(x-7)2+10125,
当x=7时,w取得最大值为10125.
答:该品牌洗碗机在去年7月销往农村的销售金额最大,最大是10125万元.
20.【答案】解:∵与墙平行的边的长为x(m),
则垂直于墙的边长为: =(25﹣0.5x)m,
根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
21.【答案】(1)解:将点B和点C的坐标代入y=a2+2x+c,得
解得
∴该二次函数的表达式为y=-x2+2x+3
(2)解:若四边形POPC是菱形,则点P在线段CO的垂直平分线上;如图,连接PP,则PELCO,垂足为E,
∵C(0,3),
∴E(0, ),
∴.点P的纵坐标等于 。
∴-x2+2x+3=
解得x1= ,x1= (不合题意,舍去),
∴点P的坐标为( , )
(3)解:过点P作y轴的平行线与BC交于点2,与OB交于点F,
设P(m,-m2+2m+3),设直线BC的表达式为y=kx+3,
则3k+3=0,解得k=-1.
∴直线BC的表达式为y=-x+3.
∴Q点的坐标为(m,-m+3),
∴QP=-m2+3m.
当-x2+2x+3=0,
解得x1=-1,x2=3,
∴AO=1,AB=4,
∴S四边形ABPC=S△ABC+S△CPQ+S△BPQ
=- AB·OC+ QP·OF+ QP·FB
= ×4×3+ (-m2+3m)×3.
当m= 时,四边形ABPC的面积最大。
此时P点的坐标为( , ),四边形ABPC的面积的最大值为
22.【答案】解:∵PB=6﹣t,BE+EQ=6+t,
∴S= PB BQ= PB (BE+EQ)
= (6﹣t)(6+t)
=﹣ t2+18,
∴S=﹣ t2+18(0≤t<6).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
